基于小波变换算法的普朗铜矿爆破振动信号能量分布研究

刘明武，黄永辉，李争荣，贾皓琦，甘等俊，李洪超，张智宇

（1.云南迪庆有色金属有限责任公司，云南 迪庆 674400；2.昆明理工大学电力工程学院，云南 昆明 650500；3.昆明理工大学国土资源工程学院，云南 昆明 650093；4.昆明理工大学城市学院，云南 昆明 650051）

0 引言

地下矿山爆破面临十分复杂的环境[1-2]，井下爆破产生的地震波、冲击波、飞石等对井下巷道、支护和工业设施等会造成严重的破坏。炸药爆炸能量除一部分对爆区主体产生影响外，还有相当一部分转化为振动、噪声和冲击波。而在大部分的爆破振动监测中，只将最大振动速度作为评判安全依据，忽略了爆破振动能量在频域上分布是不均匀的。即使整体爆破振动速度没有达到临界值，但是在某频段的能量集中也可能导致事故的发生[3]，因此，有必要对爆破振动的时域特征进行进一步的讨论。龙翼等[4]利用决策树分类算法能有效识别岩体破裂信号，消除噪音信号的影响。鲁超等[5]利用小波与EMD 算法得出测点信号能量熵随频率降低呈先增后降的趋势。汪平等[6]通过HHT 分析了小间距巷道爆破时，相邻的巷道爆炸洞壁处振动能量大部分集中于40 Hz。何理等[7]对开挖巷道的上方边坡进行爆破振动监测并进行小波分析，发现随着距离增加，能量衰减呈现先急速后平缓的趋势。张声辉等[8]通过EMD 算法对爆破振动信号主成分进行了提取，发现EMD 算法分解出来的IMF 分量呈现出一定尺度范围的模态。韦啸等[9]通过EEMD 算法对信号进行分析，得出隧道爆破能量一般集中在5～80 Hz，且主要分布在50 Hz 以下低频段。部分学者[10-13]通过EMD 算法、EEMD 算法、HHT 算法等对爆破振动信号进行能量研究，但是EMD 算法存在明显的缺点，比如端点混叠效应、模态混叠效应等并不能很好地对爆破振动信号进行研究分析，而且在大部分的爆破振动监测中，只将振动幅值最大速度作为评判安全依据，忽视了爆破振动能量在频域上的分布情况。

为解决上述EMD 算法等出现端点混叠效应以及不能精确分析爆破振动能量在频域上的分布情况等问题，可采用小波变换算法进行分析。目前有学者[14-19]采用小波变换算法、改进的小波算法以及分形理论等方法对爆破振动信号的频率、能量分布特征进行研究，利用小波分析可以将爆破振动信号按照不同的主振频带对信号进行分解及重构，从而能够更加精准地评价爆破振动危害。

本文以普朗铜矿为背景，通过数据处理软件对自然崩落法钻爆施工过程中采集到的爆破振动数据进行分析，借助小波变换算法、HHT 算法、STFT 算法研究普朗铜矿爆破振动信号能量衰减规律，为普朗铜矿自然崩落法钻爆施工过程中底部结构在爆破振动荷载下的稳定分析提供依据。

1 小波变换算法和HHT 分析法

1.1 小波变换算法

小波变换算法是将小波函数处于不同分解水平上，窗口尺寸随分解水平变化的情况下，进行信号时域局部分析，计算见式（1）。

式中：ψ（t）为一个基本小波函数或母小波函数；L2（R）为能量限量的信号空域；t为时间，s。

将 ψ（t）滑移和伸展得以取得1 组小波。对于接连不断的情形，计算见式（3）。

式中：ɑ为尺寸因素；b为伸展因素。对于失散情形，计算见式（4）。

由式（3）和式（4）可知，在爆破振动领域处理振动信号使用最多的小波基为db8，因此，本文选用小波基为db8。

子频带能量分布：将被剖析信号拆分到第n层，假定与Sn，j呼应的能效为En，j，计算见式（5）。

式中：Xj，k为重组信号Sn，j（t）的散落点的波谱幅值；j=0,1,2,…,2n-1；k=0,1,2,…,m；m为信号散落取样基数。

设被分析信号的总能量为E0，计算见式（6）。

每个频谱的能量占被解析信号总能量的比率，计算见式（7）。

由式（5）～式（7）可获得信号经过小波包分解之后不同子频带内的能量情况，进而可发现爆破振动信号传播时能量变换的规律。

1.2 HHT 分析法

希尔伯特变换（HHT）是对非稳态爆破振动信号进行时频分析的一种方法，突破了傅里叶变换分析方法（FT 变换）的局限性，计算见式（8）和式（9）。

式中：PV为柯西主分量；xi（t）为爆破振动的分量；ci（t）为振动信号的第一个分量。

将振幅H（ω，t）对时间T积分，得到Hilbert 的边际谱h（ω），计算见式（10）。

式中：ω为频率；H（ω，t）为爆破振动信号的振幅。

Hilbert 的瞬时能量IE（t）是将振幅H（ω，t）的平方对频率积分得到，计算见式（11）。

2 爆破振动监测及分析

2.1 工程概况

普朗铜矿所采用的自然崩落法在国内及世界范围内均处于先进水平。矿山位于香格里拉，其岩体以块状石英二长斑岩、石英闪长玢岩为主，岩石坚硬，中等稳固，围岩稳定性较好。本次拉底爆破设计孔数为144 个；孔网参数最小抵抗线为2.0 m；最大孔底距为1.9～2.4 m；孔网密集系数为0.95～1.20；设计装药总长度为772.4 m；装药系数为70.2%；炸药总用量为2 295 kg；每米深孔崩落矿量为5.45 t/m。

2.2 测点布置及监测成果

选定南部区域S12N 巷道爆区为试验对象，爆破总药量为2 295 kg，最大单响装药量为579.4 kg。依次把爆破测振仪放置在S13N 巷道、S13S 巷道、S14N 巷道、S14S 巷道，传感器X轴方向对准爆区，整体布置情况如图1 所示，爆破振动测试仪离爆区最近距离约为50 m，离爆区最远距离约为200 m，具体爆破振动监测成果见表1。

表1 爆破振动监测成果Table 1 Results of blasting vibration monitoring

图1 测点布置图Fig.1 Layout of measuring points

2.3 振动波能量分布衰减情况

为了更好地分析出振动波能量分布衰减情况，对S13N 巷道、S13S 巷道、S14N 巷道、S14S 巷道进行监测，一号机、二号机爆心距分别为50 m、100 m，距离爆区较近，将其归类为爆区近区；三号机、四号机爆心距分别为150 m、200 m，距离爆区较远，将其归类为爆区远区，具体振动信号波形如图2 所示。由图2 可知，四台爆破振动测试仪测出的振动波形时间均在2 000 ms 以内，其波形紧密程度不一。通过小波变换算法对任意一个振动波形进行分解，得到6 个模态分量IMF，具体情况如图3 所示。

图2 爆破振动波形Fig.2 Blasting vibration waveform

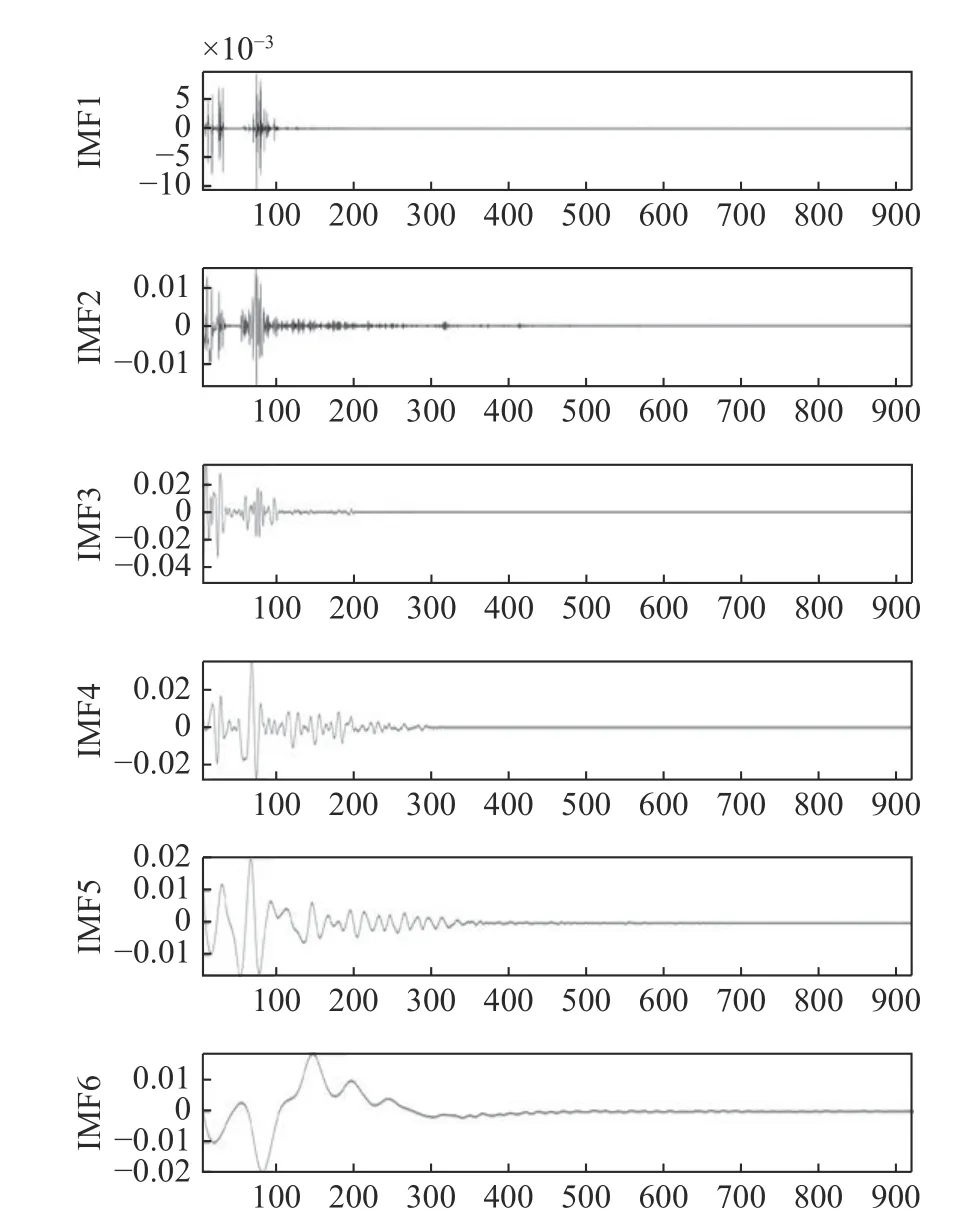
图3 IMF 分量Fig.3 IMF component

由图3 可知，模态分量IMF 在局部频带区间上呈由高到低的有序排列，同时表现出高频、低幅值和波长短等特征，这些成分是原始信号在复杂环境监测条件下受噪声干扰的重要组成部分，充分证明小波变换算法能够有效反映信号的局部性特征。

当爆破振动信号频率超出爆破振动测试仪的最小工作频率后，则可能引起信号失真。因此，当采用小波变换算法对爆破振动信号进行分解时，其分解层数要根据爆破振动测试仪的工作频带来确定[20-21]。此次爆破振动测试仪工作频率为16 kHz，为了进一步开展爆破振动能量衰减的研究，运用小波变换算法对爆破振动信号进行九层的小波分解，选用db8 作为本次分析的小波基，根据Nyquist 定理，其频率为8 kHz，小波为九层分解，则有512 个小波包，最低频带为0～15.62 Hz。根据小波变换算法，分别把4 个振动信号分解成8 个频率段，每个频率段的能量占比具体情况如图4 所示。

图4 0～125 Hz 能量占比Fig.4 Percentage of 0-125 Hz energy

由图4 可知，振动波传播到50 m、100 m 时，其能量分布情况为第2 频率段能量占比上升达到最高而后减小；振动波传播到150 m、200 m 时，其能量分布情况为第4 频率段能量占比上升达到最高而后减小。将每个频率段能量占比数值化，见表2。

表2 能量分布情况Table 2 Distribution of energy

由表2 可知，一号机、二号机最高子频带能量占比位于第2 频率段，能量占比分别为24.4%、25.3%，三号机、四号机最高子频带能量占比位于第4 频率段，能量占比分别为22.9%、21.9%。在15.62～＜31.2 Hz频率段，一号机、二号机能量占比24.4%、25.3%，三号机、四号机能量占比10.8%、10.1%，爆区近区比爆区远区能量占比平均多出14.1%；在46.87～＜93.75 Hz频率段，三号机、四号机能量占比61.7%、58.7%，一号机、二号机能量占比37.8%、45.3%，爆区远区比爆区近区能量占比平均多出18.65%。结果表明，爆区远区较爆区近区，在46.87～＜93.75 Hz 频率段能量较高，能量分布相对集中，第4 频率段、第5 频率段、第6 频率段能量占比均高于爆区近区。

通过把4 个爆破振动波形的每条子频带能量占比画成折线图，可以看出不同爆心距的爆破振动波形能量运动趋势，具体如图5 所示。

图5 能量运动趋势Fig.5 Trend of energy movement

由图5 可知，一号机、二号机能量运动趋势为在第2 频率段能量占比达到最大，在后续的频率段中能量占比迅速减小；三号机、四号机能量运动趋势为在第1 频率段、第2 频率段、第3 频率段能量占比缓慢增加，直到第4 频率段能量占比达到最大，在第4频率段、第5 频率段、第6 频率段能量占比相较一号机、二号机减少速度较为缓慢，三号机、四号机较一号机、二号机能量分布更为宽广。

结果表明，爆破振动波在传播距离较近时，能量会在短时间内迅速上升而后会随着时间增加能量占比迅速减小，且能量分布不密集；振动波在传播距离较远时，能量上升速度缓慢并且能量分布相对较集中。

2.4 振动波HHT 频谱分析

HHT 算法在信号处理和故障诊断中被广泛应用，该方法由小波变换算法和希尔伯特-黄变换两部分组成。小波变换算法可以将信号分解成多个子带，从而获取模态分量IMF。IMF 是原始信号的本征模态，可以反映出信号的局部特征。希尔伯特-黄变换可以将IMF 转换成瞬时频率和能量值，进一步分析其时变性和频域特征，具体效果如图6 所示。

图6 边际谱能量分布Fig.6 Energy distribution of marginal spectrum

由图6 可知，爆破振动能量无论传播距离的远近，其能量主要分布在0～200 Hz 之间。由图6（a）和图6（b）可知，离爆区较近的区域，最高能量幅值均超过2×10-4dB，集中在0～50 Hz；由图6（c）和图6（d）可知，离爆区较远的区域，其能量幅值均在1.8×10-4dB，远远不如爆区近区的能量幅值，最高能量幅值分布在50～100 Hz 之间。通过HHT 算法分别将爆区近区、爆区远区能量三维化，计算得出能量三维图，具体效果如图7 所示。

图7 能量三维图Fig.7 Three-dimensional diagram of energy

由图7 可知，爆区近区、爆区远区能量三维图运动趋势对应了图6 边际谱能量分布规律，爆区近区大部分能量分布在0～50 Hz，爆区远区大部分能量分布在40～80 Hz。爆区远区0～50 Hz 之间的部分能量小于爆区近区的能量，爆区远区50～80 Hz 之间部分能量大于爆区近区能量。爆区近区能量主要分布在0～50 Hz，且整体能量分布趋势相对较窄，爆区远区大部分能量分布在40～80 Hz，且整体能量分布趋势相对较宽。爆区近区能量在达到最高点以后迅速衰减，爆区远区能量在达到最高点以后衰减缓慢，且能量分布相对集中。

2.5 振动波短时傅里叶变换分析

短时傅里叶变换（STFT）是时频分析方法之一，该方法把信号划分为时间域内的几个短时段，并在每一个短时段内对窗函数加窗，然后进行傅里叶变换以获得各个时刻的频率分量。STFT 算法比离散傅里叶变换及连续傅里叶变换有更高的时间分辨率及频率分辨率。为进一步研究爆破振动波能量衰减规律，采用STFT 算法对爆区近区、爆区远区振动波形所含能量进行STFT 变换运算，如图8所示。

由图8 可知，图中Z轴代表能量功率谱幅值，爆区近区能量高功率幅值均在8.59～14.23 dB/Hz，时间分布在0.13～0.23 s，爆区远区能量高功率幅值均在8.35～11.98 dB/Hz，时间分布在0.15～0.35 s。爆区近区能量高功率幅值普遍大于爆区远区能量高功率幅值，是由爆破振动传播距离不同而产生的差异。爆区近区、爆区远区功率谱密度时频三维图后续走向也存在差异，随着爆破振动传播的增加，爆区远区的能量在达到最高点以后较爆区近区能量衰减缓慢，并且时间越长，后续能量差越大，进一步证明爆区远区能量衰减较为缓慢，能量分布相对集中。

为了使振动波形中的能量功率趋势表现得更清晰，使用数据处理软件绘制出功率趋势图，具体效果如图9 所示。

图9 功率趋势图Fig.9 Trend chart of power

由图9 可知，爆区近区着时间增加功率迅速减小，且能量分布不集中，而爆区远区功率随时间增加，功率较爆区近区衰减速度更为缓慢。

3 结论

1）普朗铜矿爆区近区主振频率主要分布在15.62～＜31.20 Hz，爆区远区主振频率主要分布在46.87～＜93.75 Hz；15.62～＜31.2 Hz 频率段爆区近区比爆区远区能量占比平均高出14.1%，46.87～＜93.75 Hz 频率段爆区远区要比爆区近区能量占比平均高出18.65%。

2）爆破振动波在传播距离较近时，能量会在短时间内迅速上升，而后随主振频率增加能量占比迅速减小，且能量分布不集中；振动波在传播距离较远时，能量上升速度缓慢且能量达到最高后其后续衰减速度较为缓慢，且能量分布更为集中。

3）实测振动信号能量特征表明，基于小波包算法能量分析方法可与爆破振动非平稳信号匹配，不仅准确了解爆破振动能量-频谱分布，还给出了不同频带上的振动能量分布和衰减规律，为指导井下构筑物结构抗震设计和工程爆破监测提供分析依据。