极化和湿度对叶簇杂波统计特性影响的分析

刘炳文 平钦文 李永祯 何密*

（1.陆军军医大学生物医学工程与影像医学系, 重庆 400038；2.国防科技大学电子科学学院, 长沙 400073）

0 引 言

在野外救援、军事侦查和反恐冲突等场合中，雷达穿透叶簇探测人体目标具有重要作用。目前，人们常用具有高距离分辨力和良好近场性能的超宽带(ultrawide band, UWB)雷达穿透非金属障碍物进行人体目标探测[1-4]。根据发射波形的差异，UWB雷达可划分为脉冲无线电(impulse radio, IR)、线性调频连续波(frequency modulated continuous wave, FMCW)、步进频率连续波(stepped frequency continuous wave,SFCW)等，其中SFCW-UWB雷达兼具距离和速度分辨力，且线性度好、结构简单[5-6]，因此SFCWUWB雷达常被用于探测隐蔽环境中的人体目标[7-8]。由于人体信号微弱，且易受到环境杂波尤其是具有低频运动特性的叶簇杂波的干扰，叶簇背景下人体目标(尤其是静止人体目标)的检测尤为困难[9-10]，需要通过对叶簇杂波的统计特性进行分析和建模。文献[11-12]利用目标回波与背景杂波在统计分布上的差异性，提出一些能适应于杂波类型变化的目标检测策略和方法，从而提升叶簇下隐蔽微弱目标的探测性能。

近年来，针对不同波段、不同体制的地基雷达在不同工作场景下叶簇杂波特性的研究逐渐深入[13-16]。2008年，文献[17]基于频率范围100 MHz~3 GHz的VHF和UHF波段UWB雷达叶簇杂波的实测数据，使用最大似然(maximum likelihood, ML)参数估计以及均方根误差(root mean square error, RMSE)评价指标，比较了对数逻辑(Log-logistic)分布、对数正态(Log-normal)分布、Weibull分布和Nakagami分布的杂波统计拟合效果，发现Log-logistic分布不仅在估计的模型参数上实现了最小的标准差，而且具有最佳的拟合优度和最小的RMSE。文献[18]和[19]基于VHF和UHF波段的前向散射雷达(天线收发分置)进行了热带树叶杂波数据测量，使用RMSE评价指标对比分析了Gamma、Log-Normal、Log-Logistic、Weibull和Nakagami 5种杂波统计分布模型拟合效果，结果表明Gamma分布模型是热带树叶杂波统计特性的最佳模型。然而，叶簇环境具有多样性，气候、地形条件等外界因素都将导致其杂波特性发生变化。文献[20]和[21]讨论了雨雪等天气条件对树叶环境中多类目标(如人、木板和铁柜)分类识别性能的影响，但并未分析不同气候条件下的叶簇杂波分布特性。此外叶簇隐蔽目标探测效果还与雷达极化方式有关，姚佰栋等人[22]针对隐蔽在不同叶簇区域的静止卡车目标，开展了多种极化方式机载飞行探测实验，通过量化分析穿透不同类型叶簇探测目标的信杂比(signal to clutter ratio, SCR)，研究了低频机载合成孔径雷达（synthetic aperture radar，SAR）的最佳极化探测方式，但上述研究并未分析极化探测方式下叶簇杂波的特性，仅对不同极化方式下SCR进行了比较。

本文基于采集多类型叶簇环境中地基SFCWUWB雷达在不同极化方式和干湿条件下探测静止人体目标的实测数据，对极化方式和湿度条件对叶簇杂波统计特性的影响进行研究，采用多种适于描述叶簇杂波幅度的统计分布模型对不同叶簇杂波特性进行描述，通过计算拟合分布和实际分布之间的RMSE定量比较杂波统计模型的拟合精度，通过多类型叶簇杂波建模及相关估计参数分析极化方式和湿度条件的影响。

1 杂波统计建模

地基叶簇SFCW-UWB雷达进行叶簇杂波统计特性建模流程如图1所示。首先对雷达回波原始数据进行信号预处理，包括混频、逆傅里叶变换(inverse Fourier transform, IFT) 和动目标显示(moving target indication, MTI)[23]等，得到一维距离像；然后根据已标定的定标体所在距离单元的平均幅值校正多通道幅值特性；最后对不同极化方式和不同湿度条件下的两种叶簇杂波的对应距离单元分别绘制杂波幅值直方图，分析杂波幅值统计特性，并比较杂波统计特性分布模型拟合效果，确定最优杂波拟合分布模型，得到模型的参数估计范围。下面分步骤进行介绍。

图1 叶簇杂波统计建模分析方法流程图Fig.1 Flowchart of statistical modeling analysis method for foliage clutter

1.1 雷达信号预处理

设SFCW-UWB雷达发射SFCW周期信号，周期为T(又称为脉冲重复时间)，信号起始频率为f0，频率间隔为∆f，每个周期内包含N个等间隔频率的正弦连续波信号，雷达工作带宽B=N∆f，发射波形如图2所示。

图2 SFCW-UWB雷达发射波形时频域图Fig.2 Schematic of SFCW-UWB radar transmission waveform in time-frequency domain

记雷达发射的SFCW信号St(t)为

式中：rect(·)为矩形窗函数；t为快时间。记τ为慢时间，则目标在R(τ)处接收到的回波信号Sr(t)可以表示为

式中：A为潜在目标反射信号的幅度；c为光速；R(τ)为潜在目标和雷达之间随慢时间变化的距离，主要指人体呼吸运动、体动和树叶随风摆动等微动叠加在径向静止距离引入的位移。

将雷达回波信号与发射参考信号混频，得到差频信号Sb(t)为

在2017年9月21日，国务院下发了《关于深化环境监测改革提高环境数据质量的意见》文件，对强化环境监测的必要性予以论述，并对目前出现的主要问题、解决方案策略作出声明。环境监测是实现环境保护的必然之路，是环境执法工作开展的前提和基础。另外，根据2016年11月1日国办发文件《“十三五”环境监测质量管理工作方案》，环境监测囊括大气污染监测、水污染监测以及土壤监测这3个方面，需要各级党政机关、相关机构组织等全面参与。

式中：∗为求复共轭；4πf0R(τ)/c为目标位移导致的慢时间上相位变化。对差频信号每个周期的数据沿快时间采样方向进行IFT，得到一维距离像，表达式为[24]

1.2 多通道幅值校正

由于不同通道间模拟器件响应和电路频率响应存在差异，加上多天线的频率响应、方向图、信号传播不同，导致多通道信号之间存在幅度值不均衡的问题，需要进行校正。本文采用三面角标准定标体校正各个通道的幅值差异。通过多次测量空旷篮球场中三面角的回波幅值，得到定标体所在距离单元上各通道幅值的平均值，以多通道幅值最大值为基准，设定补偿因子为1，其他通道的补偿因子为最大值的幅值与其幅值之比。得到补偿因子后依次与各通道相乘，可以消除通道幅度值的不均衡。水平极化探测和垂直探测通道幅值校正后的补偿因子如表1所示。通道幅值校正对于同一通道杂波数据统计特性无影响，但对于多个通道合并的数据则能减小通道不平衡对杂波统计特性的影响，校正能更准确反应杂波幅值分布。

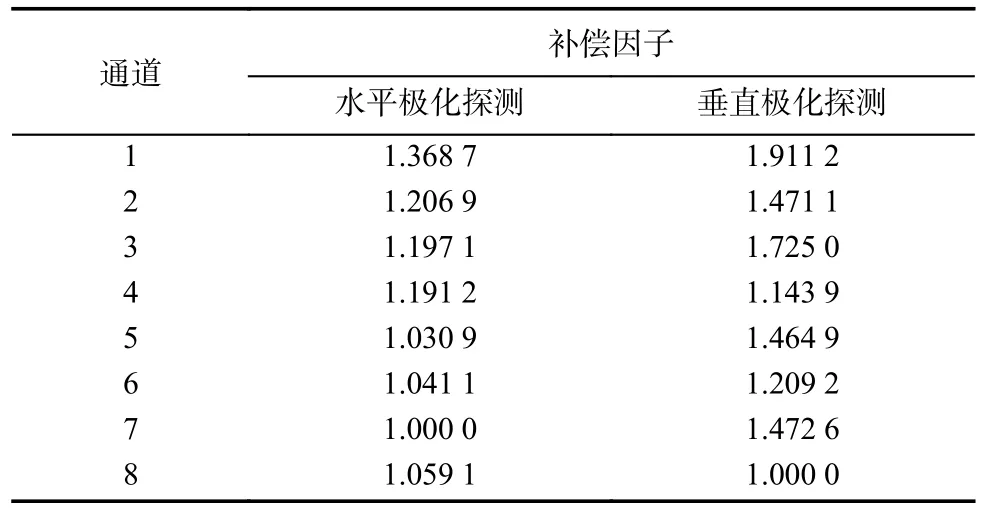
表1 多通道幅值校正的补偿因子Tab.1 Compensation factors of multi-channel amplitude correction

1.3 杂波直方图绘制

直方图简单直观，适用于分析雷达回波数据的幅值分布特性，但分组过多会导致高度参差波动，甚至出现空档，而分组过少将掩盖组内偏差，对分布状态反映不灵敏[25]。为准确反映杂波数据本身的分布形态并客观比较拟合效果，本研究选用Square-Root方法[25-26]确定雷达回波数据幅度直方图分组数和分组间距。Square-Root方法使用数据采样点数的平方根确定直方图分组个数，具有快速、简便、准确的特点[25]。

1.4 叶簇杂波分布模型探讨

常用的叶簇杂波幅度概率分布模型有经验分布模型和基于广义中心极限定理的分布模型，根据实测杂波数据，本研究重点探讨5种常用的叶簇杂波分布模型，其概率密度函数(probability density function, PDF)或特征函数(characteristic function，CF)如表2所示。

表2 常用叶簇杂波分布模型Tab.2 Common distribution models of foliage clutter

1.5 杂波拟合方法选取

准确的参数估计是得到准确的叶簇杂波统计模型的关键。本研究采用ML估计法对叶簇杂波进行分布拟合。ML估计法是在已知总体分布类型条件下，利用样本所提供的信息来求取PDF中未知参数的估计量，其基本原理如下：

假设有N个独立分布的杂波数据幅度值x1,x2,···,xN，待估计杂波模型参数为向量θ=(θ1,θ2,···,θJ)，J为杂波模型参数的个数，对于其中一个参数θj，得到杂波模型的似然函数为

1.6 拟合优度评估

假设杂波幅度离散观测值为xi(i=1,2,···,N)，其杂波数据直方图的幅度值和统计拟合模型的幅度值分别为p(xi)和q(xi)，则RMSE度量为

RMSE度量反映了拟合分布对实际数据的拟合程度，RMSE越小，拟合程度越高。

2 实测实验

2.1 SFCW-UWB雷达系统

本文采用SFCW-UWB多发多收(multiple-input multiple-output, MIMO)雷达，定标实验场景如图3所示，定标体距雷达距离为6 m，三面角定标体边长为30 cm。实验中雷达的参数如表3所示。

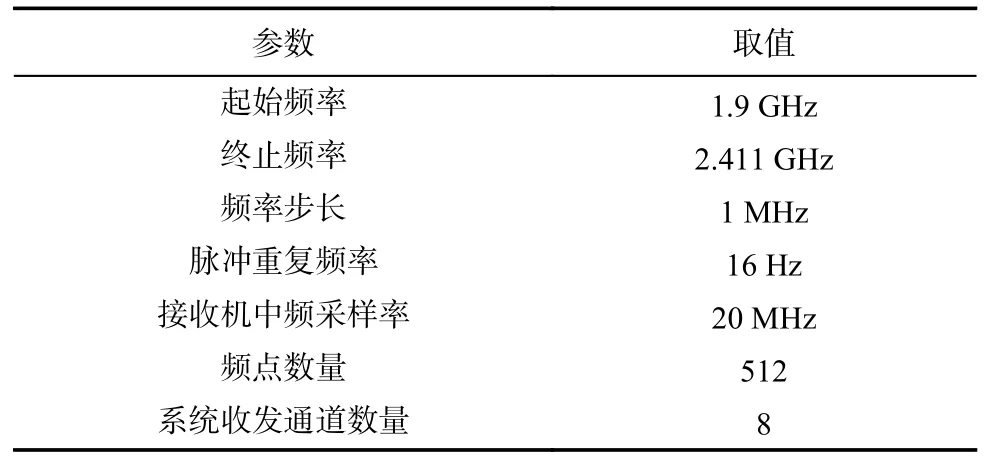
表3 SFCW-UWB雷达实验系统参数Tab.3 Experimental system parameters of SFCW-UWB radar

图3 SFCW-UWB雷达定标实验场景Fig.3 Calibration experiment scene of UHF band SFCWUWB radar

雷达采用2发4收的MIMO天线，频率为UHF波段。脉冲压缩中IFT点数为1 024，采集的回波数据以三维数字矩阵的形式进行存储，第一维表示快时间，采样点数为512；第二维表示慢时间，采样点数为480；第三维代表通道，共8个通道。通过对雷达原始数据在快时间维度和慢时间维度依次进行IFT运算，得到目标距离和速度信息，然后将相应距离单元的8个通道数据合并进行直方图分析，可以增大数据量，更准确地反映叶簇杂波统计特性。

2.2 实验设计

2022年1 月至2022年5月期间在陆军军医大学校园内利用地基叶簇SFCW-UWB雷达进行实验，选取灌木丛和乔木树林两种环境进行隐蔽静止人体目标探测。为衡量不同极化方式和不同湿度条件对杂波统计特性的影响，根据环境湿度差别，实验分别在晴天干燥（湿度54±2%，温度33±3℃）和雨后潮湿（湿度86±4%，温度11±1℃）的树林环境下以水平和垂直极化模式进行探测。在每个实验场景下，雷达分别采集叶簇环境下目标的回波数据以及叶簇杂波的数据，每种组合重复测量3次，每条数据至少记录30 s，共得到328条数据(其中包含目标和杂波的164条数据，以及仅包含杂波的164条数据)。地基雷达系统在实验中保持静止不动，认为地表及地面静物相对于雷达静止不动。该实验方案通过陆军军医大学伦理委员会批准(批准号：AF/SC-08/1.0，2021年)。

图4展示了两种典型叶簇环境下雷达探测人体目标的实验场景，雷达中心距地高度约为1.2 m，根据实际测量距离标记人体目标所在距离单元。灌木丛由密度大的叶片组成，叶片直径大小约为2 cm，高度约为1.7 m；乔木树林主要由大量的乔木组成，树木直径为10~20 cm，高度约为5 m，间隔2~4.5 m栽种。

图4 叶簇环境雷达探测人体目标的实验场景示意图Fig.4 Experimental scene of human detection using radar in foliage environment

3 实验结果和分析

受限于雷达功率，10 m以外的远距离叶簇隐蔽目标难以探测，而2 m以内目视距离缺乏研究价值，所以本研究主要分析2~10 m中等距离时雷达极化方式、湿度条件对不同类型叶簇杂波统计特性的影响。

对2~10 m距离范围内叶簇均匀分布的环境，间隔0.8 m选取10个距离单元绘制直方图，结果如图5所示。可以看出，多个距离单元的直方图围绕拟合曲线上下波动，形态上较一致。由于2~10 m中等距离范围内直方图形态相似，我们以其中一个距离单元为例，对灌木和乔木树林叶簇环境杂波进行杂波特性分析。由于本研究的最终目标是探测叶簇环境中的人体目标，在研究叶簇杂波特性时，叶簇杂波距离单元的选择应与人体目标所在距离单元保持一致，因此选择灌木环境距离单元为35、乔木树林环境距离单元为25进行研究。

图5 灌木和乔木环境杂波一维距离像与2~10 m内多个距离单元的叶簇杂波直方图Fig.5 1D range profiles and foliage clutter histograms of multiple range bins within 2–10 m of shrub and arbor environment

3.1 极化方式的影响

表4为中等距离下灌木和乔木两种不同叶簇杂波实验环境中杂波分布拟合的RMSE。表4中不同分布的最小RMSE已用下划线表示，可以看出：穿透灌木探测时，无论在水平极化还是垂直极化条件下，最优拟合分布均为Weibull分布；而穿透乔木树林探测时，最优拟合分布与极化方式有关，水平极化探测时为Log-logistic分布，垂直极化探测时为Weibull分布。

表4 不同叶簇杂波实验场景的5种杂波分布拟合的RMSE值Tab.4 RMSE values of 5 clutter distribution fittings in different foliage clutter experimental scenes

3.1.1 灌木环境

灌木环境中水平极化和垂直极化的最优拟合分布均为Weibull分布，RMSE分别为0.004 7和0.003 5，相同条件多组实验数据拟合后得到的尺度参数α和形状参数β估计范围如表5所示。图6所示为探测距离为5 m时，雷达水平极化与垂直极化模式下叶簇杂波在距离单元35的幅度分布直方图，此时，雷达垂直极化相比水平极化探测，直方图形态上更窄、拖尾更短，形状参数β取值更大，说明灌木环境中水平极化和垂直极化的最优拟合分布虽然均为Weibull分布，但是参数范围有差别。

表5 灌木环境不同极化方式下最优分布拟合的参数估计值Tab.5 Parameter estimation of the optimal distribution fitting in shrub environment using different polarization modes

图6 灌木环境不同极化方式杂波分布直方图拟合情况Fig.6 Distribution fitting of shrub clutter histogram using different polarization modes

3.1.2 乔木环境

乔木环境中水平极化和垂直极化的最优拟合分布与极化方式有关，水平极化探测时最优拟合分布为Log-logistic分布(RMSE为0.004 6)，垂直极化探测时最优拟合分布为Weibull分布(RMSE为0.004 2)，相同条件多组实验数据拟合后得到的参数估计值范围如表6所示。乔木距雷达3.6 m，树木所在距离单元为25，杂波幅度分布情况如图7所示，垂直极化探测高大树木幅度分布直方图较为扩散，而水平极化探测时分布较为聚集。由于树干回波是杂波的主要来源，树干回波给乔木杂波带来了很长的拖尾，所以在水平极化探测时，Log-logistic分布能更好地描述这种“拖尾性”。在雷达垂直极化探测时，回波大部分来自于树冠和地面的散射，使用适合描述地杂波的Weibull分布更能保证拟合的效果和精度。

表6 乔木环境不同极化方式下最优分布拟合的参数估计值Tab.6 Parameter estimation of the optimal distribution fitting in arbor environment using different polarization modes

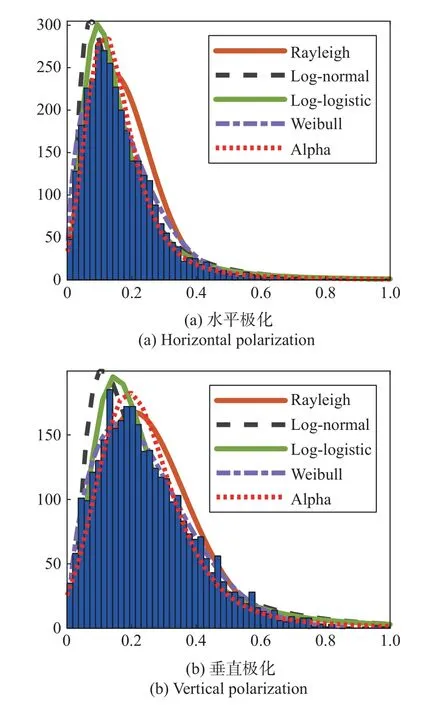
图7 乔木环境不同极化方式杂波分布直方图拟合情况Fig.7 Distribution fitting of arbor clutter histogram using different polarization modes

3.2 湿度条件的影响

利用多组实验数据对不同湿度条件下灌木环境和乔木环境杂波分布进行拟合，其中，灌木杂波距离单元为35，乔木杂波距离单元为25，统计结果如图8和图9所示，5种分布拟合RMSE值如表7所示，参数估计范围如表8所示。可以看出：灌木在潮湿和干燥两种条件下，最优拟合分布均为Weibull分布；乔木环境水平极化探测时不论潮湿和干燥条件，叶簇杂波最优拟合分布均为Log-logistic分布，RMSE分别为0.004 8和0.005 0，而垂直极化探测时不论潮湿和干燥环境，叶簇杂波最优拟合分布均为Weibull分布，RMSE分别为0.004 8和0.007 6，这与乔木环境杂波最优拟合分布结果一致。从表8可以看出，灌木在垂直极化探测、乔木在水平极化探测时，均是干燥条件比潮湿条件最优拟合分布的形状参数取值更大，直方图的形态更宽。

表7 不同湿度条件下叶簇杂波5种分布拟合的RMSE值Tab.7 RMSE values of 5 distribution fittings of foliage clutter under different humidity conditions

表8 不同湿度条件下叶簇杂波最优分布拟合的参数估计值Tab.8 Parameter estimation of the optimal distribution fitting of foliage clutter under different humidity conditions

图8 灌木环境不同湿度条件下杂波分布直方图拟合情况Fig.8 Distribution fitting of shrub clutter histogram under different humidity conditions

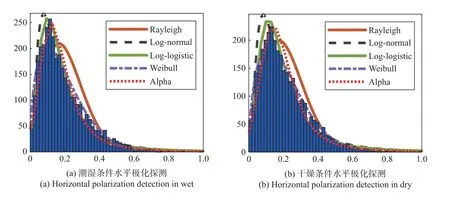
图9 乔木环境不同湿度条件下杂波分布直方图拟合情况Fig.9 Distribution fitting of arbor clutter histogram under different humidity conditions

4 结 论

本文基于地基UWB雷达实测叶簇穿透探测目标回波数据，采用5种适于描述叶簇杂波幅度的统计分布模型对比分析了两类叶簇杂波统计特性。结果表明不同极化方式探测灌木时的杂波最优拟合分布均为Weibull分布，极化方式仅对参数的取值范围有影响；而乔木树林杂波在不同极化方式下的最优拟合分布不同，水平极化和垂直极化下分别为Loglogistic分布和Weibull分布。灌木环境垂直极化探测最优统计分布为Weibull分布，参数α范围为1.778 9~1.805 8，β范围为1.839 6~1.910 7，RMSE为0.003 5；乔木树林环境水平极化探测最优统计分布为Loglogistic分布，参数µ 范围为0.387 1~0.404 9，σ范围为0.215 3~0.272 4，RMSE为0.004 6。湿度条件并不改变叶簇杂波最优拟合分布类型，仅改变分布形参的取值范围。在最优极化条件下，湿度增大时，灌木最优拟合分布形参范围由1.747 2~1.864 9变为1.848 9~1.897 4，乔木最优拟合分布形参范围由0.173 3~0.227 6变为0.242 7~0.306 5。总体上湿度越大最优拟合分布的形参取值越大，直方图更宽、拖尾更长。本文得到灌木和乔木树林两种叶簇杂波分别在不同极化方式和不同湿度条件的最优拟合分布和相关参数的范围，为提升叶簇下人体目标探测性能提供了理论和实践参考。但是，本研究没有进一步探讨如何利用不同条件下叶簇杂波的统计特性和参数估计以提升地基UWB雷达探测叶簇下隐蔽目标的性能，而且本研究中的雷达发射功率有限，因此仅考虑了近距离下叶簇杂波的统计特性和人体目标检测特性，下一步将对不同条件下杂波背景人体目标检测方法进行研究。