二级公路“2+1”车道布局模式关键设计参数研究★

陶涵韬，马丽安娜，向 健，王 杰，况爱武

(1.长沙理工大学交通运输工程学院,湖南 长沙 410114; 2.新疆交通规划勘察设计研究院有限公司,新疆 乌鲁木齐 830000)

0 引言

二级公路在我国公路网中占据重要地位,一般采用双向两车道布局,该布局模式需借助对向车道超车,难以满足车辆行驶过程中的超车需求,尤其当对向交通量接近饱和时,由于无法超车而导致本向车道车辆的排队不断延伸,造成通行效率低下;如果本向车辆强行进入对向车道借道违规超车,则极易造成正面碰撞事故,通行安全难以保障。“2+1”车道布局模式的提出为上述问题提供了一个有效的解决思路。

“2+1”车道布局最早在法国实施[1],随后在瑞典、德国、爱尔兰、美国、韩国等[2]其他国家也开展了一定的研究与实践。各国针对“2+1”车道布局的研究各有差异,主要体现在道路横断面形式、“2+1”车道的应用条件等方面。国外实践表明“2+1”车道对改善二级公路交通安全、提升效率均是有效的。国内针对二级公路“2+1”车道解决超车问题的研究较少,工程实践仅见于山东青岛的省道S210海阳段。目前,国内外在超车方面的研究多集中于双向两车道公路如何安全超车,如任炜从超车视距的安全性角度研究了如何借用对向车道超车,对满足超车视距的超车路段长度进行了分析[3];余姝源等对双向两车道的车辆自主超车轨迹进行了规划与跟踪控制研究[4];张文会等就借助对向车道超车可能发生的碰撞问题设计了超车安全间距控制模型[5];岳全胜等对双向两车道公路的超车行为演化博弈开展了分析,为研究驾驶行为动机提供了一种新的方法[6],但上述研究均未涉及在增设超车道情形下的超车安全和超车效率等问题,难以解决安全超车、提升效率等困局。

为缓解双车道公路超车难问题,程国柱等率先提出附加车道理念,并对其适用的交通条件进行了研究,该理念通过在原有公路路基的外侧增设超车道来解决超车问题[7],随后,吴立新等对附加车道的设置参数开展了研究[8]。附加车道的设置虽然能有效解决单侧超车问题,但该布局模式会增加路基宽度,在大幅度增加投资的同时多占有限的土地资源。张水涛提出了“2+1”超车道模型,通过将超车道设置于公路中央,双向交替设置,用“渐变段+缓和段”进行转换,并进一步对公路相关几何参数开展了初步设计,但未充分考虑超车的安全性和该模式适用的交通条件[9]。

从研究现状来看,目前对“2+1”车道布局模式与国内双车道驾驶行为、道路交通条件的结合仍缺乏系统研究,超车段长度、分合流段长度等关键设计参数的确定仍存在盲区,部分借鉴交叉口渐变段、设计规范要求等获得的参数经验取值其合理性仍有待考究。为此,本文以二级公路“2+1”车道布局模式为对象,针对部分关键设计参数取值现有研究存在的不足,构建了理论分析模型,并以安全保障及效率提升为目标对理论模型获得的参数取值开展了仿真评价,以期能促进“2+1”车道布局模式在我国二级公路上的应用落地。

1 二级公路“2+1”车道布局模式

本文针对路基宽度在12.5 m及以上的二级公路,提出了一种介于双向两车道、双向四车道之间的“2+1”车道布局模式,该布局包括1条行车方向交替的内侧超车车道和2条行车方向固定的外侧基本车道,其中内侧超车车道仅供行驶速度相对高的小汽车通行,该种车道布局模式见图1。

如图1所示,“2+1”车道公路的基本路段由超车段、分流段和合流段三部分组成。超车段的同向车道之间采用虚线分隔,对向车道采用双实线或柔性护栏分隔。超车段的中间车道供行驶速度较快的小汽车通行,分流段与合流段应采用填充标线进行渐变。

针对图1所示的“2+1”车道布局模式,本文对其超车段、分流段、合流段等关键设计参数进行理论研究,以确定各项关键参数的最优长度。

2 二级公路“2+1”车道关键设计参数理论模型

为便于模型表达,用A表示超车车辆,B表示被超车车辆,模型中各参数的具体含义如表1所示。

表1 参数的含义表

2.1 超车段长度计算模型

如图1所示,超车段长度有两种表示方法。

方法(1):超车段长度应满足车辆安全距离与车身自身长度要求,因此,超车段长度应满足式(1):

LC1=H1+L2+SB+H2+L1+SA3

(1)

方法(2):车辆在超车时,超车过程可分为加速阶段SA1、匀速超车阶段SA2、并道阶段SA3三个阶段,具体过程如下:

1)加速阶段SA1:此阶段超车车辆从跟驰状态改为加速超车状态,超车车辆A确认安全后改变车道,并入超车车道的同时提高车辆速度,达到合适的超车速度并稳定行驶,其中超车速度应满足对应道路的限制速度。

2)匀速超车阶段SA2:达到合适超车速度后,在超车车道上稳定行驶过程中利用超车速度和原车道被超车辆的速度差匀速超越被超车辆,直至超车车辆在超车车道上与原车道上的被超车辆到达安全距离,确认安全后行驶回原车道。

3)并道阶段SA3:在超车车辆确认达到安全后行驶回原车道直至在原车道稳定行驶。

因此,为满足超车条件,根据超车过程的三个阶段,超车段长度计算方法如式(2)所示:

LC2=SA1+SA2+SA3

(2)

根据交通安全理论和规范,超车车辆在超车过程中所行驶的距离应满足如下关系式(见式(3)):

SA1+SA2≥H1+L2+SB+H2+L1

(3)

故有式(4):

LC2>LC1

(4)

综上,超车段长度仅需满足车辆基本行驶约束条件下的最小值即可,故超车段长度用LC1来表示极限状态下超车道长度的最小值。因此,超车段长度计算公式见式(5):

LC=LC1=H1+L2+SB+H2+L1+SA3

(5)

1)设计速度参数(V)。根据JTG B01—2014公路工程技术标准,二级公路的设计速度有80 km/h,60 km/h两种。同时,规范规定,作为干线的二级公路,其设计速度宜采用80 km/h,受地形、地质等条件限制,可采用60 km/h;作为集散的二级公路,设计速度宜采用60 km/h,受地形、地质等条件限制,可采用40 km/h。因此,根据规范要求,本文在“2+1”车道布局关键参数分析研究中主要考虑60 km/h和80 km/h两种设计速度情况。

2)车身长度参数(L)。布局“2+1”车道的主要目的是为小型车辆提供更多超越大型车辆的超车机会,根据GB/T 15089—2001机动车辆和挂车分类中对各类车辆车身长度规定,在式(5)中,超车车辆A和被超车辆B的车身长度L1,L2均满足此规范要求,分别取值为7 m和12 m。

3)车辆间安全距离参数(H)。车辆间的安全距离可表示为式(6):

H=S制动+d

(6)

考虑到“2+1”车道布设应用于二级公路,超车段设置的条件有限,应考虑极限条件下的超车,从道路驾驶安全的角度考虑,安全距离的计算宜采用最小安全距离模型,此模型在计算最小安全距离时综合考虑了车辆的制动特性、前方出现障碍物或前方车辆遭遇险情突然停止的情况。图2刻画了车辆在制动过程中减速度随时间的变化。

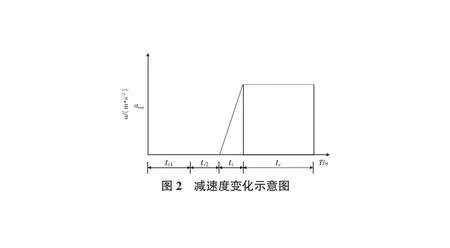
图2中,tr1表示驾驶员的反应时间;tr2表示驾驶员转换脚踏板的动作时间,考虑到在tr1,tr2两个时间内车辆的行驶状态不变,故二者之和用tr表示,一般取值为0.8 s～1.0 s;ti表示制动器在磨合过程中车辆减速度的增长时间,一般取值为0.1 s～0.2 s;tc为车辆达到稳定的减速度后进入匀减速运动过程的时间。根据各时间段车辆行驶状态,可将各时间段内车辆行驶距离分别表示为Sr,Si,Sc。

tr为驾驶员的反应阶段,此时段内车辆行驶状态不发生改变,故速度不变,因此,车辆行驶的距离Sr为(见式(7)):

Sr=vBtr

(7)

在车辆制动阶段,假设制动减速度与时间成线性关系,从零线性增长到车辆的最大制动减速度amax,则在ti时段任意时刻t,车辆的速度值v(t)为(见式(8)):

(8)

根据距离与速度的关系,通过对式(8)中的t进行积分,可得车辆在减速度增加阶段的行驶路程Si为(见式(9)):

(9)

令t=ti,则式(9)可改写为式(10):

(10)

其中,amax为车辆最大减速度,一般取值6 m/s2～8 m/s2。

在tc阶段,车辆达到最大减速度并做匀减速运动,制动减速度恒为amax。根据图2,如果在tc阶段末,车辆刚好完成制动减速过程,则tc大小可表示为式(11):

(11)

故车辆在tc匀减速阶段所行驶的距离为(式(12)):

(12)

综上,车辆总的制动距离为三个阶段所行驶的距离之和,表达式如式(13)所示:

(13)

(14)

由式(14)可知,车辆的安全制动距离与两车处于跟驰状态时的初速度vB、驾驶员的反应时间tr、制动减速度增长时间ti和最大制动减速度amax等因素有关[11]。结合式(14),式(6)可表示为式(15):

(15)

结合我国二级公路设计速度取值,根据式(15)可得“2+1”车道车辆间安全距离如表2所示。

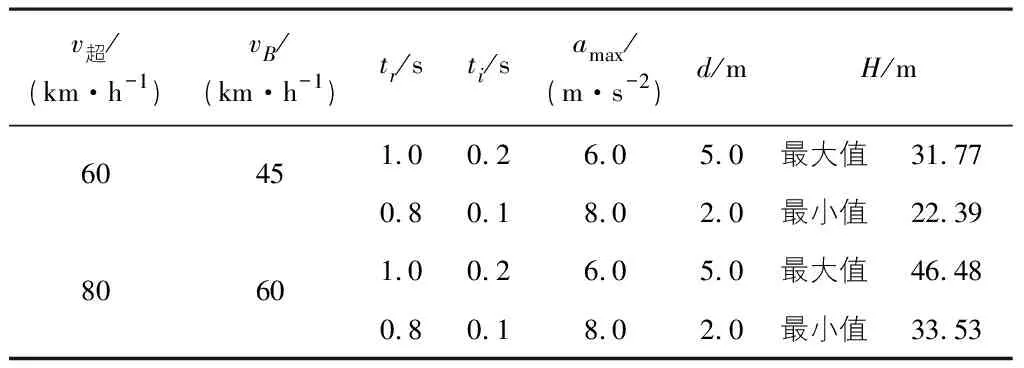
表2 “2+1”车道车辆间安全距离计算参数

4)并道安全距离参数(SA3)。并道是指超车车辆在超车道完成超车后与被超车辆保持安全距离的前提下换道并入原车道的过程,并道期间超车车辆A保持超车速度超越被超车辆。在并道过程中,面对突发状况需足够的反应时间,根据已有研究[12],在实际超车过程中,车辆从本车道并入另一条相邻车道的过程一般至少需要3 s以上,并且严禁连续并两条以上的车道。据此,并道安全距离参数可表示为式(16):

SA3=v超t合并

(16)

根据式(16)可计算得到各种超车速度下的并道安全距离参数,如表3所示。

表3 各种超车速度下的被超车速度与并道安全距离

5)被超车辆行驶距离(SB)。分析被超车辆B的行驶过程,假定车辆A为匀加速,在A车超越B车、并在超车车道上与B车达到安全距离的过程分为两个阶段,即:

a.A车改变车辆行驶状态,从跟驰状态改为匀加速阶段,在此过程中车辆A完成车辆加速达到超车速度和并入超车车道两个驾驶动作。

b.A车达到超车速度后保持匀速,利用超车车辆与原车道被超车辆之间的速度差Δv稳定超越被超车辆B,直到达到两车间的安全距离。

设阶段a车辆A所用时间为tA1,阶段b车辆A所用的时间为tA2,由此即可计算得到车辆B在此过程中的行驶距离SB(见式(17)):

SB=vB(tA1+tA2)

(17)

其中,阶段a满足式v超-vA=atA1,故可得tA1的计算表达式如式(18)所示,式中a取舒适加速度,为3.4 m/s2。

(18)

记阶段a与阶段b过程中A车的行驶距离分别为SA1和SA2,其中SA1为匀加速阶段,SA2为匀速超车阶段,则SA1与SA2可表示为式(19),式(20):

(19)

SA2=v超tA2

(20)

考虑车辆安全距离与车身长度要求,在阶段a与阶段b过程中A车的行驶距离为:

SA1+SA2=H1+L2+SB+H2+L1

(21)

结合式(17)—式(21),可得tA2(其中在跟驰状态下设vA=vB),如式(22)所示:

(22)

代入式(17),并结合式(18),即可得SB(见式(23)):

(23)

根据表达式(23),可以得到各种速度条件下SB的取值如表4所示。

表4 各种速度条件下的SB值

在分析得到H1,H2,L1,L2,SB,SA3等参数的取值后,即可根据式(5)计算得到各种不同速度条件下的超车段长度,如表5所示。

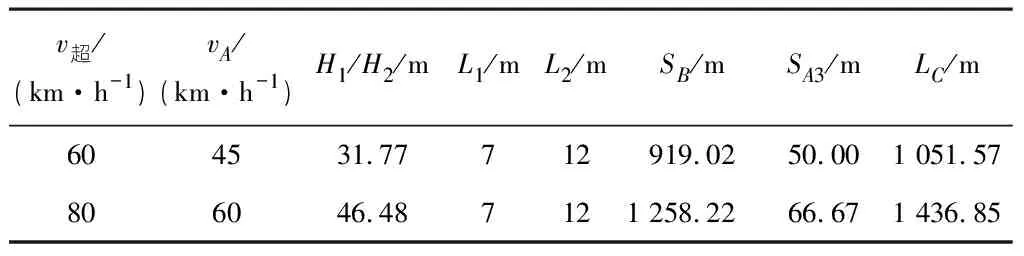
表5 各种速度条件下的超车段长度(LC)

2.2 合流段长度计算模型

依据GB 5678.3—2009道路交通标志与标线,“2+1”车道合流渐变段长度(LHj)宜采用如式(24)计算:

(24)

合流段总长度包括2倍的合流渐变段长度(LHj)、1倍的缓冲段长度(LHh)。依据GB 5678.3—2009道路交通标志与标线,缓冲区段LHh长度应不小于15 m。

因此,合流段长度可表示为式(25):

LH=2LHj+LHh

(25)

根据式(25)计算得到不同车速、车道宽度下合流段最小长度见表6。

表6 合流段的最小长度

2.3 分流段长度计算模型

分流段长度LF包含渐变段LFj和缓冲区段LFh,根据文献的研究和计算方法,分流段长度计算模型如式(26)所示:

LF=2LFj+LFh

(26)

其中,分流渐变段长度LFj取值宜为合流渐变段长度LHj的1/2倍～2/3倍,且应不小于30 m。因此,根据式(26)计算可得到各种速度条件下的分流段长度取值如表7所示。

表7 分流段长度取值

3 仿真测试

基于VISSIM仿真平台,搭建二级公路“2+1”车道布局场景,仿真路段长度5 km,分合流段采用第2节计算的理论长度,重点对超车段长度及其适应交通量进行仿真测试。

针对不同超车段长度(0.7 km,0.8 km,0.9 km,…,1.8 km)、不同双向小时交通量(500 pcu/h,900 pcu/h,1 300 pcu/h,1 700 pcu/h)、不同车型比例(大型车占比10%,20%,30%)、不同设计速度(60 km/h,80 km/h)进行组合测试。考虑超车率(取每辆小型车辆在一个超车段内的平均超车次数)、路段平均行程速度(取仿真区间内单车道和双车道方向的平均值)、合流段平均停车次数(取一个超车合流区段3 min内出现的停车次数)作为评价指标[13-14],评估“2+1”车道布局模式下超车段的适宜长度及适应的交通条件。超车率越大,则意味着为小型车提供的超车机会越多;合流段平均停车次数越少,则停车延误越少且运行越顺畅。以大型车比例为30%、设计速度80 km/h场景为例,各种不同流量及超车段长度下的仿真结果如图3所示。

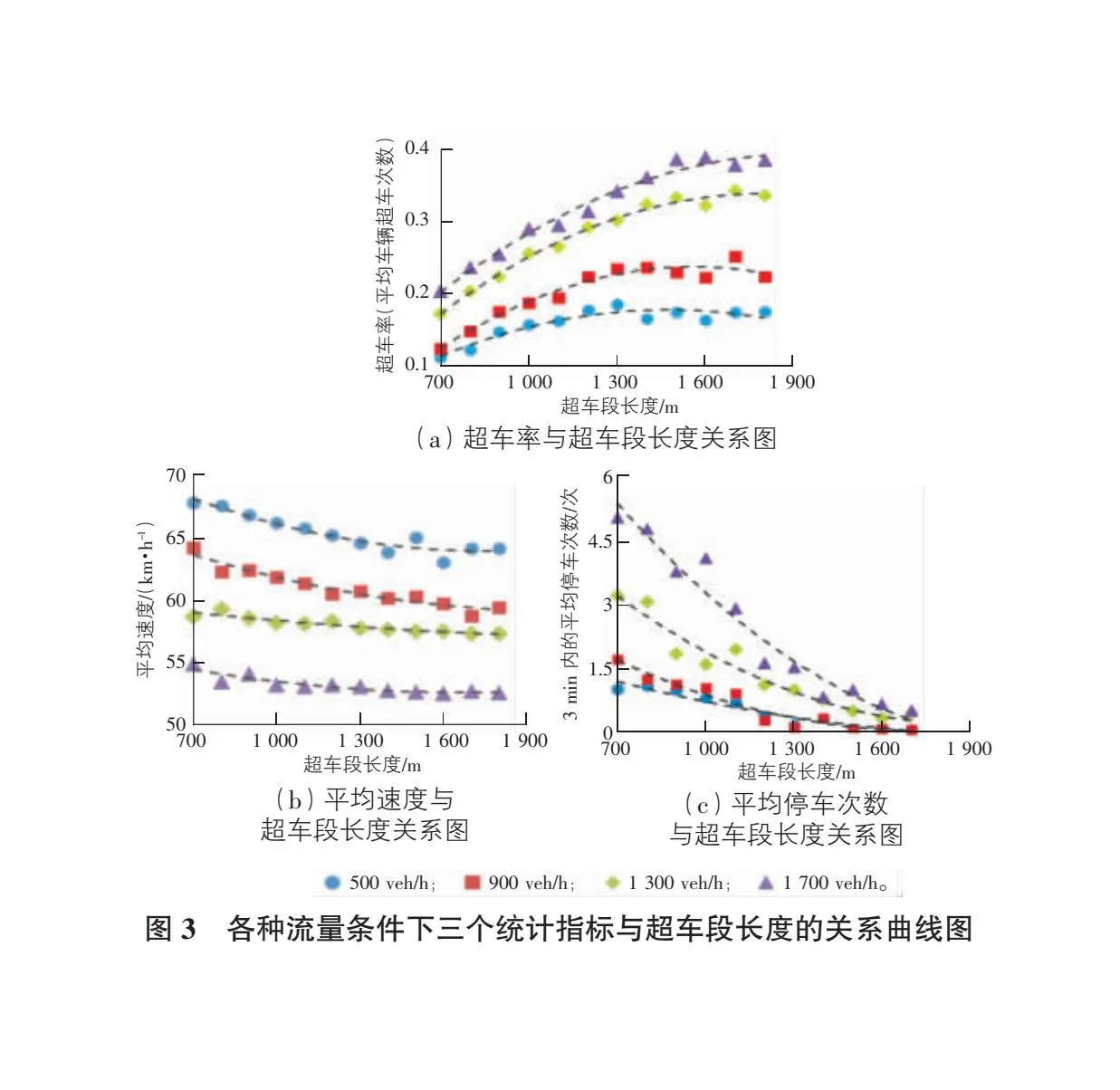
从图3可以发现:1)超车率随流量和超车段长度的增加而增加,在低流量条件下(如低于900 pcu/h),当超车段长度超过1.2 km后,超车率基本趋于稳定,在高流量条件下(如超过1 300 pcu/h),当超车段长度超过1.6 km后,超车率基本趋于稳定;2)平均速度随流量的增加而减小,超车段长度对平均速度的影响较小;3)在各种超车段长度下,平均停车次数均随流量的增加而增多,但随着超车段长度的增加,平均停车次数的增幅逐渐放缓;4)低流量条件下,当超车段长度超过0.8 km后,停车次数较少,高流量条件下,当超车段长度超过1.2 km后,停车次数较少。

以流量1 000 pcu/h,大车占比30%为场景,分别对设计速度为60 km/h和80 km/h的路段进行仿真,获得平均车速与超车段长度的关系曲线如图4(a)所示;以流量1 000 pcu/h,设计速度80 km/h为场景,分别对不同大车占比开展仿真,获得平均停车次数与超车段长度的关系曲线如图4(b)所示。

从图4可以发现:1)各种设计速度条件下,超车段双向平均速度均随超车段长度的增加呈现先升后降的趋势,当设计速度60 km/h,超车段长度为1.0 km左右时平均速度达到峰值;当设计速度80 km/h,超车段长度在1.2 km左右时平均速度达到峰值。2)各种大型车占比条件下,平均停车次数均随超车段长度的增加呈现单调下降趋势,说明超车段长度越长车辆越容易完成超车,但当超车段长度相同时,大车占比越高造成的停车次数越多,表明车辆越难以完成超车。

根据规范,二级公路适应的流量宜为5 000 pcu/d～15 000 pcu/d,换算为高峰小时交通量约为500 pcu/h～1 500 pcu/h。在满足理论最小长度的基础上,综合考虑仿真测试,可以得到60 km/h和80 km/h两种设计速度以及不同流量条件下“2+1”公路超车段长度的取值建议范围如表8所示。

表8 二级公路“2+1”车道布局超车段长度的建议取值范围

4 结论

1)本文针对我国现状二级公路超车效率低、超车安全保障不足等困局,提出了“2+1”车道布局模式。

2)构建了超车段长度、分合流渐变段长度等关键设计参数的理论计算模型,并根据模型及规范,计算出“2+1”车道超车段长度、分合流渐变段长度的合理取值。

3)基于VISSIM仿真平台,对从理论模型获得的关键设计参数开展了仿真分析,并给出了不同设计速度以及不同流量条件下“2+1”车道超车段长度的建议取值。

论文研究表明,针对二级公路实施“2+1”车道布局并通过设置适宜的超车段长度,在保障交通安全的同时有助于提升交通运行效率,在有实施条件的二级公路上可逐步开展试点示范。