黄河流域碳排放、科技创新与产业结构优化——基于Moran’s I与PVAR 的实证分析

刘建华 ，施天乐，黄亮朝

（1. 郑州大学 管理学院，河南 郑州 450001；2. 郑州大学 黄河生态保护与区域协调发展研究院，河南 郑州 450001；3. 克劳斯塔尔工业大学 地下能源系统研究所，克劳斯塔尔-采勒费尔德，德国）

温室气体排放引起的环境问题日趋严重，发展低碳经济已成为共识[1-2]。中国碳排放位居全球第一，亟须将生态保护和高质量发展建设放在突出地位，加强科技创新和优化产业结构，严格把控“高耗能、高排放”行业的发展[3-4]。黄河流域以能源化工、原材料、农牧业等产业为主导，高知识、技术含量的战略性新兴产业规模较小，生态环境和经济高质量发展矛盾突出[5]，因此深入探究碳排放、科技创新和产业结构优化之间的关系对于黄河流域实现生态保护和高质量发展具有重要现实意义。

国内外学者对碳排放、科技创新和产业结构优化展开了大量的研究。关于碳排放和科技创新的相关研究颇为丰硕，但结论存在较大差异，就科技创新对碳排放的作用而言，部分学者认为科技创新能降低碳排放强度且研发投入对生产要素密集型企业的碳生产率存在正向推动作用，其原因在于科技创新可以有效促进可再生能源取代化石能源，进而降低社会对传统能源的依赖，减少碳排放量[6-7]；但也有部分学者指出科技创新对碳排放量的影响并不一定显著，甚至导致碳排放量的增长[8-9]；还有学者认为碳排放与科技创新之间存在“回弹效应”，产出效率、碳排放量和科技水平都在大幅增加，因而并不能明确科技创新与碳排放的具体关联[10]。关于科技创新与产业结构优化，较多学者对其互动关系进行了研究。部分学者认为科技创新单向推动产业结构优化且空间溢出效应较为明显，通过加大要素投入力度、更新设备和提升生产水平可以较好促进产业结构优化[11-13]，其他学者则认为科技创新与产业结构优化具有双向互动作用，并构建面板模型对二者的双向关系进行研究，发现二者间存在良性的互动关系且地区差异较大[14-15]，随着时间推移二者互动关系减弱。而关于碳排放与产业结构优化的研究主要体现在三方面：第一，运用投入产出模型、回归分析等方法研究产业结构优化对碳排放的作用；部分研究表明第二产业对区域碳排放影响强度最高且恒为正值[16-17]，也有研究发现中国第三产业的增长会抑制碳排放量[18-19]。第二，基于STIRPAT 等模型分解碳排放影响因素，探究产业结构优化对碳排放的影响；采用LEAP 等模型对碳排放进行预测分析[20-21]。第三，通过灰色关联度模型、耦合协调度模型等方法对不同区域碳排放与产业结构的耦合性、关联性进行了研究，结果显示第二产业和碳排放的关联度最大[22]。

综上所述，关于碳排放、科技创新和产业结构优化的相关研究取得了较多成果，但仍存在不足，需进一步讨论。首先，现有文献大多是对碳排放、科技创新、产业结构优化中的两两关系进行研究，鲜有将三者纳入同一个框架进行研究的学术成果，缺少与三者相关的机制分析；其次，大多数研究其尺度较宏观，基于国家、省级层面较多，对碳减排政策制定缺乏有效支撑且并未有针对黄河流域的研究成果。因此，本文以黄河流域57个地级市2010—2020 年的面板数据为基础，测算碳排放、科技创新与产业结构优化三者间的耦合协调度并进行可视化分析，运用Moran’s I 探究三要素之间的空间相关性，并通过PVAR 模型进一步探究其互动关系，以期为黄河流域生态保护和高质量发展提供科学的决策支持。

1 作用机制分析

如图1 所示，碳排放对科技创新和产业结构优化存在双向效应。碳排放的增加带来气候变暖、空气质量下降、海洋酸化等问题，加剧环境污染。一方面，过大的环境负荷影响经济社会健康发展，迫使国家加大对环境治理的投入，即将本用于发展科技创新及升级产业结构的资源优先转移到减污降碳，进而减缓科技创新与产业结构优化进程[23]。另一方面，环境污染的加剧会增强人们对清洁能源和环保技术的需求，进而推动能源产业结构优化和绿色科技进步，提升可再生能源的使用率和促进高新环保企业发展，一定程度上倒逼科技创新与产业结构升级优化。

图1 碳排放、科技创新和产业结构优化作用机制

科技创新推动科技进步、设备更新，通过成果转化提升生产效率并减少资源在开发、运输、使用过程中的损耗，拓展开发清洁、可再生能源的渠道，降低企业对传统能源的依赖，最终实现对碳排放的抑制。科技创新能显著推动产业结构优化。科技创新通过创造新需求和构建产学研互动共享平台两种机制来带动产业升级[24]。创新动力源于新需求的出现，新需求催生新产品和新产业部门，两者形成全新的产业链，进而推动产业结构的演进。产学研共享平台的构建使科技创新完成上游、中游、下游（科研机构、高校、产业）的对接与耦合，加快黄河流域信息、技术、人才流动，提升生产要素流动速率，进而带动产业升级。

产业结构优化主要从合理化、高级化、高效化三个方面影响碳排放和科技创新。产业结构合理化、高级化与高效化促进资源合理配置、社会生产效率提升和社会分工细化[25]。一方面提高社会能源的利用效率、减少能源浪费，从而降低产品生产的能耗，进而降低碳排放水平；另一方面改善能源消费结构，减少高碳能源的使用率，利于清洁能源的推广和新能源企业的发展，抑制了碳排放。产业结构合理化、高级化与高效化促进技术、人才、知识密集型产业进步，也带动产业向金融化方向转型。技术、人才、知识密集型产业的发展与集聚为科技创新带来了新的活力，其发展所需要的创新资源规模大，能够有效带动上下游产业创新能力的提升[14]。产业结构向金融化方向发展能开拓多样化筹集创新资金的渠道，能有效降低科技创新的风险，促进创新水平的提升。

2 研究设计

2.1 研究区域

黄河流域流经9 省份——青海、四川、甘肃、宁夏、陕西、河南、山西、内蒙古、山东。综合考虑政府规划、沿黄省市行政区划的完整性以及经济社会发展与黄河流域的关联性等，本文主要选取了黄河流域干流及主要支流核心区所在的57 个地级市作为研究对象，如图2 所示。其中，上游包括兰州、白银、武威、定西、陇南、西宁、呼和浩特、包头、通辽、鄂尔多斯、巴彦淖尔、乌海、银川、石嘴山、吴忠、固原和中卫17 个地级市，中游包括天水、平凉、庆阳、洛阳、三门峡、焦作、太原、大同、阳泉、长治、晋城、朔州、晋中、运城、忻州、临汾、吕梁、西安、铜川、宝鸡、咸阳、渭南、延安、榆林和商洛25 个地级市，下游包括郑州、开封、安阳、鹤壁、新乡、濮阳、济南、淄博、东营、济宁、泰安、德州、聊城、滨州和菏泽15 个地级市。

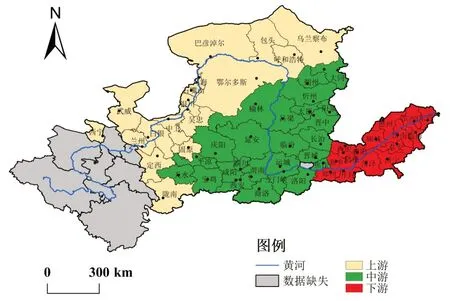
图2 研究区域

2.2 变量选择

本文涉及碳排放、科技创新、产业结构优化水平三个变量，其中对碳排放数据进行标准化处理，而科技创新及产业结构优化在构建指标体系后通过熵权法对其进行赋权处理。

2.2.1 碳排放量的测算

鉴于黄河流域地区的能源类别及分布情况，本文采用联合国政府间气候变化专员会（IPCC）的测算公式来估计CO2的排放量，以煤炭、焦炭、原油、汽油、煤油、柴油、燃料油、天然气和电力作为主要消耗能源的代表，具体计算方法如下。

式中：CO2表示碳排放量，Ei表示各类能源的消耗量，NCVi表示第i种能源的平均低位发热量，CCi表示第i种能源单位热量的含碳水平，COFi表示第i种能源的氧化因子，12、44 分别为碳与二氧化碳的分子量。各能源消耗系数如表1 所示。

表1 不同能源标准煤折算系数与碳排放系数

2.2.2 科技创新水平

参考现有研究[14]从科创投入、产出两方面来衡量各市科技创新水平。其中，科创投入选取科创过程中投入的R&D 人员、R&D 经费及教育财政比重等因素；科创产出的表现形式主要有专利授权量、科技论文及其他科技产出等，如表2 所示。

表2 科技创新评价指标体系

2.2.3 产业结构优化水平

选取合理化、高级化、高效化三个维度衡量产业结构的优化程度，如表3 所示。因为结构偏离度和泰尔指数存在诸多缺陷[25]，因此本文选取加权结构偏离度衡量产业合理化程度。产业结构层次指数和高新技术产业产值占GDP 比例能很好体现产业结构从一产向二产、三产递进的过程，因此选取二者作为衡量产业高级化的指标。产业结构高效化侧重产出效率，因此选取二产、三产投入产出比及产值比进行衡量。

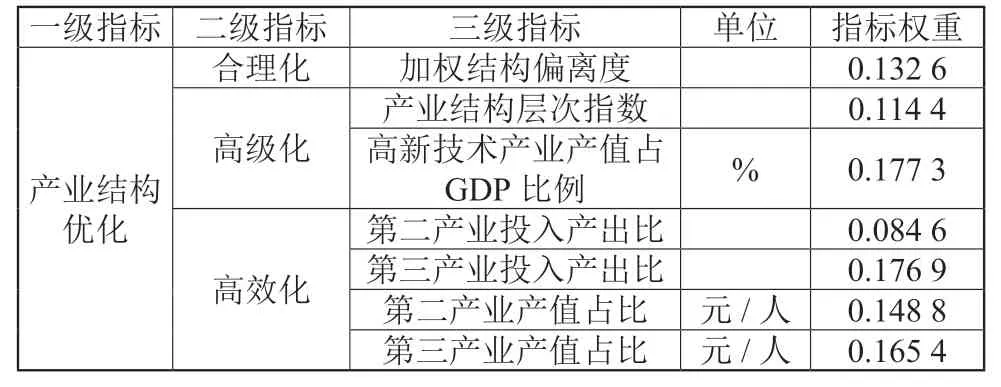
表3 产业结构优化评价指标体系

各指标数据主要来源于各市国民经济与社会发展统计公报、《中国环境统计年鉴》、各市统计局、《中国城市统计年鉴》、各地区统计年鉴及国家知识产权局所公布的相关数据。部分缺失数据采用相邻年份均值或插值法填充。

2.3 研究模型

2.3.1 耦合协调度模型

本文在耦合度模型的基础上建立碳排放、科技创新和产业结构优化的耦合协调度模型，以下是具体步骤。

（1）碳排放—科技创新—产业结构优化耦合模型，计算耦合度M：

式中：M为耦合度，Z1表示CO2排放量，Z2表示科技创新水平，Z3表示产业结构优化水平。

（2）为更好地体现碳排放、科技创新和产业结构优化三者间的协调发展程度，改进耦合度模型建立耦合协调度模型，具体公式如下：

式中：C为各市碳排放、科技创新和产业结构的协调指数；T为耦合协调度；α、β、ε分别为碳排放、科技创新、产业结构优化的系统权重，借鉴已有的学者研究[26]及数据分布情况，令α=β=ε=1/3，并将耦合度及耦合协调度均分为10 个阶段，如表4 所示。

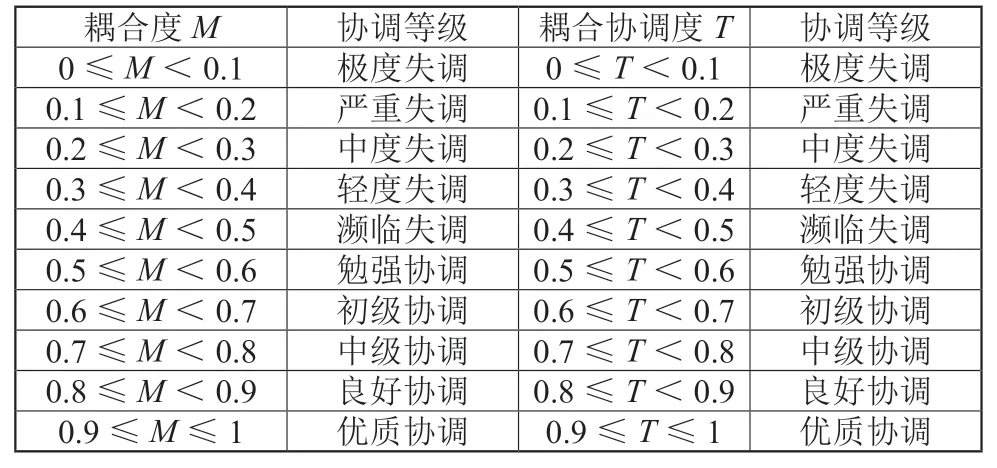
表4 耦合度和耦合协调度等级划分标准

2.3.2 Kriging插值法

Kriging 插值法以变异函数理论和结构分析为基础，是在目标区域内对变量进行无偏最优估计的一种方法[3]。对黄河流域地级市耦合协调度进行Kriging 插值分析，可以直观反映各市三要素耦合协调程度及变化趋势，计算公式如下：

2.3.3 空间计量模型

空间自相关模型主要用于研究要素间的空间关联程度，分为全局和局部空间自相关。其中全局空间自相关常采用Moran’s I 指数模型来检验区域间要素是否存在交互作用，计算公式为：

式中：I为全局Moran’s I 指数；n为黄河流域地级市数量；xi、xj分别为第i市和第j市间的耦合协调度；为平均值；wij为空间权重矩阵。

由于全局Moran’s I 指数无法得出具体单元的空间相关性，因此对局部Moran’s I 指数进行测算，其计算公式为：

式中：Ii为局部Moran’s I 指数；n为黄河流域地级市数量；xi、xj分别为第i市和第j市间的耦合协调度；wij为空间权重矩阵。

2.3.4 PVAR模型

碳排放、科技创新、产业结构优化之间存在复杂的动态关系且可能存在滞后效应[27]。当前POOL 和PVAR模型的使用较多，但前者存在内生性与序列关系问题，而后者既能考虑到个体差异，也能通过引入滞后项解决内生性问题，从而更好地体现多变量间的动态影响关系。因此选取PVAR 模型研究碳排放、科技创新、产业结构之间的动态关系，具体公式如下：

式中：Yit是一个1×3 阶的列向量，包含碳排放、科技创新和产业结构优化水平三个内生变量；α0为截距项；j为滞后阶数；αj为滞后j阶的参数矩阵；βi为个体固定效应；δi为个体时点效应；εit为随机扰动项。

3 结果分析

3.1 总体结果分析

从图3 可以看出，黄河流域2010—2020 年碳排放、科技创新与产业结构优化指数均存在明显波动。其中，碳排放指数波动最大，2010 年到2016 年较为平稳，数值从0.057 增为0.076，2016 年后呈现快速上升的态势，仅2016 年一年，碳排放指数从0.076 增加至0.158，但随着时间推移，碳排放增长速率有所下降。而科技创新与产业结构优化指数存在较为一致的变化趋势，具体来看，两者除在部分年份存在波动外，整体呈现上升趋势，发展速度增长明显。结合具体指标来看，对比2010 年，2020 年研发强度指数从0.145 提升至0.23；专利授权指数从0.023 7 提升至0.093 9；产业结构合理化指数从0.016 提升至0.055。这表明在研究期内黄河流域科技创新成效良好，产业结构升级优化效果明显。

图3 2010—2020年黄河流域三要素综合指数

3.2 可视化分析

通过ArcGIS 10.7 软件对黄河流域2010 年、2020年三要素的耦合协调度（以下简称“协调度”）进行可视化（图4、图5）。同时，为打破行政区域界限的影响，更直观地探索黄河流域三要素协调度的时空演化特征，本文运用自然间断点分级法对黄河流域2010 年、2020 年协调度进行Kriging 插值分析（图6、图7）。

图4 2010年黄河流域三要素耦合协调度可视化图

图5 2020年黄河流域三要素耦合协调度可视化图

图6 2010年黄河流域三要素耦合协调度Kriging插值图

图7 2020年黄河流域三要素耦合协调度Kriging插值图

从时间尺度来看，黄河流域整体三要素协调发展水平提升，进入协调范畴的城市由2010 年的2 个增加至2020 年的15 个。从空间尺度来看，黄河流域东西部城市差异明显，东部城市的协调发展水平较高，对比2010 年和2020 年，东部城市提升明显，协调发展出现了层次跨越，而西部城市整体虽有提升，但部分地市发展形势堪忧。此外，省会城市表现抢眼，相较于其他城市，其协调发展情况较优，辐射带动能力较强。具体来看，2010 年黄河流域三要素整体协调水平较低，其中中上游甘肃、宁夏和陕西失调程度较为严重，其协调度多小于0.4，而济南、郑州协调度均高于0.5，处于“勉强协调”阶段，太原与西安则处于“濒临失调”阶段。山东及郑州、西安等省会城市协调水平相对较高，这些城市具有一定的区位优势，交通便利，经济水平和科技创新水平较高，产业结构相对合理；而协调水平较低的城市大多位于西部，人口稀少，经济水平较低，科技创新和产业结构升级发展缓慢。对比2010 年，2020 年黄河流域协调水平增长明显，从西向东呈现“低—中—高”的分布格局，但并未出现“中级协调”及以上阶段，山东及郑州、西安、兰州等省会城市达到“勉强协调”和“初级协调”阶段。山东整体协调度维持在较高水平，聚集效应明显，但向西的辐射能力较弱，对流域整体的带动作用亟须加强，中上游东部整体协调水平上升，发展势头良好，但中上游西部如固原、庆阳、平凉等市协调水平仍相对较低，发展缓慢，亟须推动经济、科技、产业协同发展。

3.3 空间自相关分析

为深入研究碳排放、科技创新与产业结构优化三者协调度的空间格局，引入空间自相关分析，通过全局与局部Moran’s I 分析，更好地体现三者协调水平的动态演化过程。

3.3.1 全局Moran’s I分析

对黄河流域三要素空间相关性的测算，首先需构建各城市间的空间权重矩阵，本文采用地理邻接矩阵，结合公式（6），通过GeoDa 软件对面板数据进行计算得到黄河流域三要素协调度全局Moran’s I 指数，并采用MCMC 方法验证全局Moran’s I 指数的显著性状况，结果如表5 所示。由此可以看出，Moran’s I 指数均为正且通过显著性检验，表明黄河流域协调水平与空间分布显著正相关，呈现明显的“高—高”“低—低”聚集趋势。从变化趋势来看，Moran’s I 指数随时间的推进呈现在波动中上升的趋势，表明协调发展的空间聚集特征在加强，流域内地区之间的联系仍在提高。

表5 黄河流域三要素耦合协调度全局Moran’s I指数

3.3.2 局部Moran’s I分析

局部Moran’s I 能将全局Moran’s I 自相关细分到各单元，进而检验各城市的集聚情况，弥补了全局Moran’s I指数过于笼统的缺点。根据公式（7），选取2010 年、2020两个样本年份，通过GeoDa 软件计算黄河流域三要素协调度局部Moran’s I 指数并结合LISA 统计量进行说明，样本年份的LISA 聚类图如图8、图9 所示。

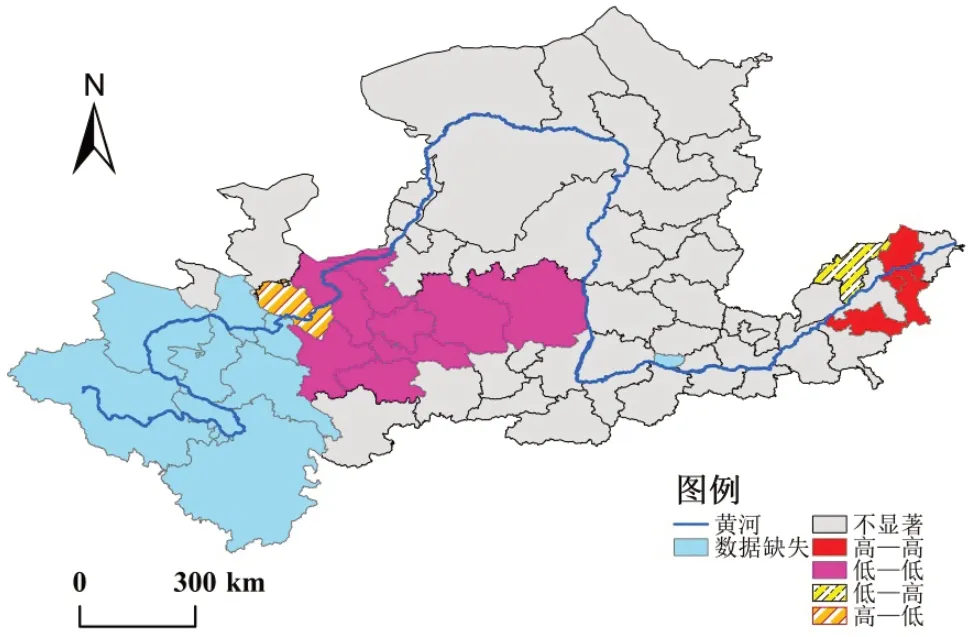
图8 2010年黄河流域三要素耦合协调度LISA聚类图

图9 2020年黄河流域三要素耦合协调度LISA聚类图

由LISA 聚类图可知，黄河流域东部和中西部分别出现“高—高”“低—低”聚集区域，表明三要素耦合协调度较高和较低的地级市均出现了聚集效应，空间上呈现带状分布。具体来看，“高—高”聚集区主要集中在山东，2010 年包括滨州、淄博和泰安，2020 年新增济南、东营、德州、菏泽、郑州5 个城市，这些城市地理位置优越、交通便利，经济发展较好，是协调发展的“热点”区域。“低—低”聚集城市数量变化较小，由2010 年的8 个减至2020 年的6 个，位于甘肃、宁夏及陕西北部，形成协调发展的“冷点”区域，与可视化和Kriging 插值分析结论较为吻合。“低—高”聚集区域的城市分布特征不明显，2010 年仅有德州，而2020 年则变为开封与濮阳，其中德州在研究期内协调度取得较大的提升，与城市积极推动减污降碳、科技发展和产业升级转型密不可分。开封与濮阳则可能受周围城市协调度较高的影响形成局部“洼地”，但仍需在未来高质量发展进程中找准定位，提高自身协调水平。“高—低”聚集区域于2010 年在兰州出现，表明兰州的周边城市诸如白银、武威、定西协调度较低，跟兰州存在较大的差距，因此形成局部“高地”。此外，经济水平与协调度的空间聚集程度存在一定关联，具体表现为在经济发展较快的东部三要素协调度较高，空间聚集性更强，易形成“高—高”聚集区，经济、科技创新与产业结构优化的发展能够对周围区域产生积极的辐射带动作用；相反，经济基础薄弱的中西部地区，交通闭塞，科技创新水平低，产业结构不合理，易形成“低—低”聚集区。

3.4 互动关系分析

三要素间的互动机制是影响协调度变化的内在原因，可视化与空间相关性分析探究了三要素协调度的时空演化特征及原因，并未很好地体现三要素间的具体关联，因此选用PVAR 模型对三要素的互动关系进行检验。

3.4.1 数据平稳性检验与最佳滞后阶数确定

为了减少“伪回归”现象对研究带来的影响，需对数据进行平稳性检验，较为常见的有LLC、IPS、HT、Hadri LM、ADF-Fisher 这五种检验方法。本文选取LLC、IPS 和HT 这三种方法对数据进行检验，检验结果如表6 所示。

表6 面板单位根检验结果

最佳滞后阶数的确定可以确保估计结果的可靠性，因此在进行PVAR 模型回归前通过对模型进行AIC、BIC 和HQIC 三种准则的计算，选择三者中值最小的模型。相关检验结果如表7 所示，AIC、BIC 和HQIC 标准的最优阶数均为滞后1 阶，因此，在本文中，PVAR模型选择1 阶滞后是最佳选择。此外，本文还进行了稳健性检验，通过对模型单位根特征值进行计算，发现三个估计点均位于单位圆之中，因此，表明PVAR 模型稳健。

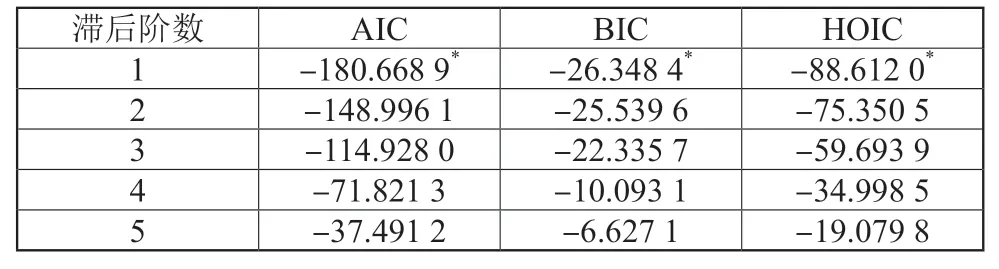
表7 模型最优滞后阶数选择

3.4.2 脉冲响应分析

脉冲响应函数能有效分析随机扰动项一个标准差的冲击对PVAR 模型中各变量的影响。本文利用MCMC方法进行模拟，结果如图10 所示，图中横轴为期数，纵轴为程度，上下线为95%的置信区间。

图10 脉冲响应结果

从脉冲响应结果可以得出：（1）当碳排放、科技创新与产业结构优化面对一个标准差的冲击时，自身立刻表现出较强的正向反应，随后逐渐降低，表明三者均存在自身加强机制，但随着时间推移，加强机制的作用逐渐减弱。（2）碳排放在受到科技创新影响时立刻出现负向反应，第1 期后反应为正并上升，这表明早期科技创新能抑制碳排放，但可能后期由于过度重视科技创新的经济效益忽略其环境效益进而导致碳排放增加[28]。科技创新受到碳排放冲击时则出现先升后降的负向效应，说明碳排放能减缓科技创新进程，可能的解释是碳排放带来环境污染，政府加大环境治理的力度，可能减少对科技创新的要素投入，进而影响科技创新水平。（3）科技创新受到产业结构优化的冲击时，立刻出现较强的正向反应，后反应强度逐渐下降，这表明早期产业结构优化能显著促进科技创新，但随着时间的增加，其对科技创新的边际效应逐渐减弱。而产业结构优化受到科技创新冲击时始终与其保持正相关，说明科技创新通过改进生产技术、创造新的需求，形成新产品和新产业部门，推动产业链的更新，有效促进产业结构优化。（4）产业结构优化受到碳排放影响的冲击影响时，当期反应为0，表明碳排放对产业升级的影响具有一定的滞后性，但其整体正相关，说明碳排放能倒逼产业结构升级优化。而碳排放受到产业结构优化冲击影响时出现了倒“U”型的正向关系，可能的原因是在0 ～10 期内碳排放增长率始终高于产业结构优化速度，但后期随着技术进步、绿色可再生能源的使用以及高新技术产业的发展，碳排放的增长速率下降。

3.4.3 方差分解

通过对预测误差进行方差分解，可以度量不同随机项对内生变量波动的贡献度。表8 为对黄河流域碳排放、科技创新和产业结构优化三个变量的预测误差方差分解的结果，列出了第1 期到第10 期的结果。

表8 方差分解结果

由表8 的方差贡献率可以看出，碳排放、科技创新与产业结构优化对自身的贡献值最大，验证了自身加强机制的存在，其中科技创新对自身的贡献率占比最高，始终维持在90%以上。从碳排放的贡献率来看，科技创新与产业结构优化占比较低，两者的贡献度较为接近，随着时间的增加，第2 期后产业结构优化的贡献度始终略高于科技创新。从科技创新的贡献率来看，由于其自身占比始终高于90%，碳排放和产业结构优化占比极低，其中碳排放的贡献率极其微弱，第6 期贡献率达到峰值，为0.7%。从产业结构优化的贡献率来看，碳排放的贡献度始终高于科技创新，科技创新在第4 期前的方差贡献率为0，第4 期后才有缓慢的增长，而碳排放的贡献率则保持稳定的增长，于第10 期达到11.3%。

4 结论及建议

本文以黄河流域57 个地级市2010—2020 年的面板数据为基础，测算碳排放、科技创新与产业结构优化的耦合协调度并进行可视化分析，运用Moran’s I 探究三要素间的空间相关性，并通过PVAR 模型进一步探究三者间的互动关系，得到以下结论。

（1）根据ArcGIS 可视化及Kriging 插值分析，2010—2020 年黄河流域碳排放—科技创新—产业结构优化耦合协调度整体有所提升，呈现“西低东高”的分布格局，山东及省会城市如郑州、太原等始终维持较高的水平。其中，济南和郑州于2020 年进入“初级协调”阶段，而甘肃、宁夏和陕西的部分城市仍处于“中度失调”和“轻度失调”阶段。

（2）黄河流域全局Moran’s I 指数整体为正且显著，“高—高”“低—低”聚集趋势明显，“高—高”聚集区多位于山东，而“低—低”聚集区则位于甘肃、宁夏及陕西北部。

（3）碳排放、科技创新、产业结构优化这三者存在较强的自身加强机制。科技创新对碳排放具有显著抑制作用，碳排放能减缓科技创新进程。产业结构优化与科技创新之间相互促进作用明显，但是随着时间的增加，产业结构优化对科技创新的促进作用下降。碳排放对产业结构优化有一定的倒逼作用，但产业结构优化对碳排放的影响并不显著。

根据以上结论，提出以下相对应的建议。

（1）提升黄河流域降碳、科技创新与产业结构优化三者协同发展的效率。黄河流域要在“双碳”目标的基础上通过技术支持、政府补贴、法律保障等方式发挥创新引领优势，加快科创成果转化，同时提升产业结构合理化、高级化与高效化水平，推动高新技术产业的进一步发展。

（2）打造区域协调发展体系。加强各地区之间的合作，聚焦黄河下游，发挥省会城市尤其是郑州、济南的带动作用，通过济郑高铁、郑渝高铁连接新欧亚大陆桥，打开山东省通往中西部地区的高铁通道，建立利益共享、风险共担的协调发展机制，促进各地区人才和技术互相流动。

（3）积极承接发达地区高新产业转移，推动低碳城市建设。黄河流域要深化与京津冀、长三角等地区的高效对接，增加创新投入，优化能源消费结构，完善创新生态与金融保障体系，依靠科技创新推动产业向低污染与高效率方向发展。