利用LMD-SVD 方法进行GNSS 坐标时间序列降噪

龚旭峥，汪香梅，王凯时

（1. 浙江省测绘科学技术研究院，浙江 杭州 310023；2. 开化县资源规划数据中心，浙江 衢州 324300）

随着全球卫星导航系统（GNSS）的不断建设与完善，目前全球多地已建立了GNSS 连续跟踪观测站。GNSS 测站的建立与卫星数据观测不仅为全球板块运动、地壳变形监测等领域研究提供了重要的基础数据，也为国际地球参考框架的建设提供了有力的技术支撑。受多种外界复杂环境影响，GNSS 测站观测数据通常包含大量噪声，严重阻碍了GNSS 数据的进一步分析与应用，因此研究如何获取更“干净”的GNSS时间序列、构建统一严密的GNSS时间序列噪声模型具有重要意义。王健[1]等研究GNSS 测站数据发现，GNSS 数据中的噪声主要包括有色噪声与白噪声，且在N、E、U 方向上的噪声特性存在差异。GNSS 测站坐标时间序列包含噪声的多样性和复杂性给降噪方法研究提出了更高的要求，目前常用的降噪方法包括奇异值分解（SVD）、经验模态分解法（EMD）、小波变换法等[2-4]。SVD方法降噪的关键在于重构奇异值个数的选取，但对包含趋势项的信号进行降噪时，奇异值个数选取会受趋势分量的影响；EMD方法降噪时受端点效应、模态混叠等因素影响，降噪效果受限；小波变换降噪时受分解层次、小波基、阈值的影响较大，降噪效果在参数选取不合适时较差。作为一种能对非线性、非平稳性信号进行自适应分解的降噪方法，局部均值分解（LMD）不会产生如EMD方法一样的负频率。LMD方法降噪是通过重构分解得到的低频乘积函数（PF）分量和余量，剔除高频分量[5]，由于没有进一步处理高频分量，导致高频分量中包含的有用信息丢失。因此，本文在LMD方法的基础上，引入SVD方法提取高频分量中的有用信息，建立了LMD-SVD 组合降噪模型，从而提高有用信息的利用率；并通过5 个IGS 测站坐标时间序列进行实验分析，以验证本文方法的有效性与优越性。

1 基本原理与方法

1.1 LMD基本原理

假设存在一原始信号x(t)，其LMD过程为[6-7]：

1）计算原始信号中局部极值点ni和对应极值x(ni)，则局部幅值ai和局部均值mi表示为：

对ai与mi进行处理，得到包络估计函数a11(t)与局部均值函数m11(t)。

2）将m11(t)从x(t)中剔除，则有：

通过a11(t)解调h11(t)，即

计算得到s11(t)包络估计函数a12(t)，判断a12(t)是否为1；若a12(t)不为1，则将s11(t)视为输入信号，计算s11(t)局部均值函数m12(t)，从s11(t)中剔除m12(t)得到h12(t) ，再利用a12(t) 解调h12(t) ；重复上述步骤，直到得到纯调频信号s1n(t)。

最终包络信号为：

式中，q为第q次迭代过程。

3）将纯调频信号与包络信号的乘积表示第一个乘积函数：

4）将x(t) 中剔除PF1(t) ，得到新的信号u1(t) ，由于PF1(t)为原始信号中频率最高分量，因此剔除PF1(t)分量后得到的u1(t)可表示为原始信号x(t)的平滑版本。重复上述步骤，直至得到一个单调函数uk(t)，停止迭代。

5）x(t)可表示为k个PF与一个残余分量uk(t)的叠加，即

式中，p为第p个PF 分量，由基于LMD 的信号分解过程可知，LMD 分解的基础为信号自身极值，不断迭代得到相应PF，信号最终被分解为残余信号和部分PF。

1.2 端点效应消除

信号在使用LMD方法进行分解时，信号的分布特征会被信号的突变点、间断点等端点破坏，从而使分解结果存在误差，称之为端点效应[8]。本文使用噪声辅助法（向原始信号中添加受控高斯白噪声）降低端点效应，则有：

式中，xi(t)为第i次加噪后信号；di(t)为第i次加入高斯白噪声；ai为噪声幅度；q为1、2。

对加噪后信号进行LMD分解得到：

取N次结果的平均值，得到基于噪声辅助法的LMD分解结果为：

式中， PFk为每个PF 分量平均结果；为每个余项的平均结果。

1.3 LMD-SVD信号降噪方法

SVD方法降噪的关键是奇异值个数的确定，本文采用奇异值差分谱准则确定奇异值个数[9]，但该方法受趋势分量影响较大，因此SVD方法适合对信号中高频分量进行降噪。高频分量与低频分量分界点的确定是实现LMD方法降噪的关键。本文通过计算连续均方根误差（CMSE）方法确定分界点[10]，即

式中，n为PF分量个数；N为信号长度。

第p阶PF 分量能量密度同样可通过式（11）表示，计算得到相邻PF 分量CMSE 后，定义CMSE 全局极小值为：

将CMSE 全局极小值对应的p值作为高频分量与低频分量的分界点，直接剔除高频分量，保留低频分量与余量，但会导致高频分量中有用信息的丢失，因此本文在LMD方法的基础上引入SVD，构建LMD-SVD方法。该方法实现信号降噪的具体步骤为：①对某一原始信号，使用LMD方法进行分解，得到若干个PF分量与余量；②计算相邻PF分量之间的CMSE值，CMSE全局极小值即为高频分量与低频分量的分界点；③针对高频分量，使用SVD方法进行分解，得到相应奇异值并根据奇异值差分谱准则确定信号重构奇异值个数；④重构经SVD方法去噪后的高频分量、低频分量与余量得到最终降噪信号，并对降噪效果进行定量评价。

2 实例分析

本文选择IGS 网站中LHAZ、BJFS、SHAO 等5 个IGS 站点2016—2019 年U 方向坐标时间序列进行处理与分析，坐标时间序列采样间隔为1 d。为降低原始序列中数据缺失以及粗差对后续数据处理与分析的影响，首先对原始坐标时间序列进行插补、粗差剔除等预处理[11]。受篇幅限制，本文仅将SHAO 站U 方向时间序列作为实验数据。

2.1 LMD方法坐标时间序列降噪

受篇幅限制，本文仅以LHAZ 测站U 方向坐标时间序列为例进行说明，首先通过LMD方法分解时间序列，得到8个PF分量与1个余量；然后计算相邻PF分量之间的CMSE 值，结果见表1，可以看出，PF 分量在第3 阶时出现CMSE 全局极小值，因此可将第3 阶PF分量认定为高频分量与低频分量的分界点；剔除前3 个高频PF 分量，对剩余PF 分量和余量进行重构，得到降噪后时间序列（图1）。

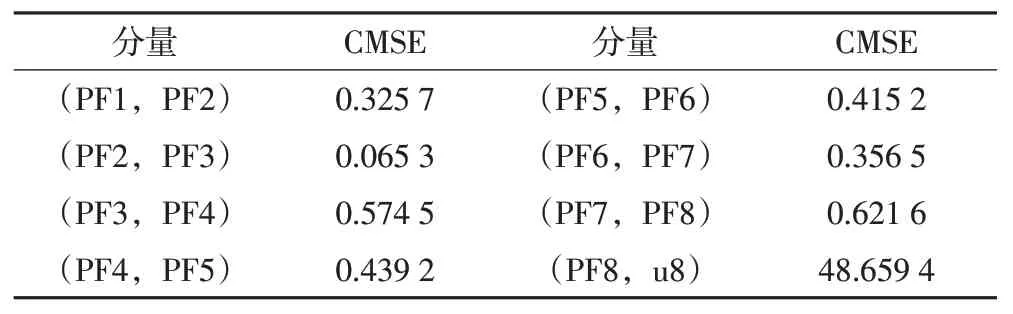
表1 相邻PF分量之间的CMSE值/10-8

由图1可知，LHAZ站U方向坐标时间序列降噪后时间序列基本反映了原始时间序列的走势，但二者之间差异较大。对原始时间序列与降噪后时间序列残差进行统计，结果见图2。

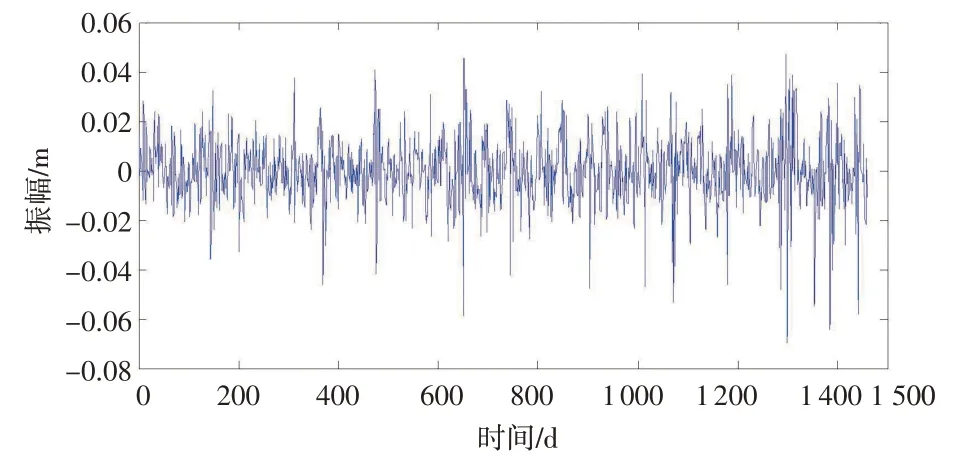
图2 LMD方法降噪后残差统计

2.2 LMD-SVD坐标时间序列降噪

为进一步提取高频噪声中的有用信息，提高原始信号中有用信息的利用率，本文利用SVD方法对前3个PF分量进一步降噪；再将经SVD降噪后得到的有用信息与剩余PF分量、余量进行重构，获取最终降噪时间序列。构建高频分量Hankel矩阵并进行SVD，计算前100个奇异值差分谱（图3），可以看出，在第5个位置出现谱峰值，而后奇异值差分谱值降低，因此选择前5个奇异值进行重构得到高频分量降噪后序列。

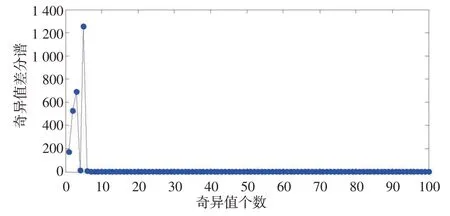
图3 LMD-SVD奇异值差分谱

重构降噪后序列、剩余PF 分量和余量得到降噪后U 方向时间序列（图4），可以看出，LMD-SVD 方法降噪得到的时间序列不仅可以准确反映原始时间序列走势，更能缩小与原始时间序列差异。统计降噪后序列的残差（图5），计算得到残差振幅平均绝对值为1.7 mm。相较于单一LMD 方法，LMD-SVD 方法降噪结果的残差平均值明显降低，能够进一步提取高频PF分量中有用信息，得到更好的降噪结果。

2.3 定量分析对比

通过上述方法对LHAZ、BJFS、SHAO等5个IGS站U方向坐标时间序列进行降噪处理，将信噪比、相关系数和均方根误差作为时间序列降噪效果的评价指标。信噪比反映有用信号与噪声的比值，值越大，表示降噪效果越好；相关系数反映降噪后信号与原始信号波形的相似度，值越大，表示降噪效果越好；均方根误差反映降噪前后信号差异，值越小，表示降噪效果越好[12-13]。

信噪比的计算公式为[14]：

相关系数的计算公式为：

均方根误差的计算公式为：

式中，n为信号长度；σx和σx̂分别为x和̂的标准差；cov(x'̂)为x和x̂的协方差；x(i)为真实信号；为降噪后信号。

对各站点U 方向坐标时间序列降噪结果进行统计，结果见表2。由图1、图4和表2可知，LMD-SVD方法对各站点坐标时间序列降噪结果的信噪比、相关系数明显提高，均方根误差明显降低。统计5 个测站各评价指标的平均值发现，相较于LMD 方法降噪结果，LMD-SVD 方法的信噪比与相关系数分别提高了34.28%与17.11%；均方根误差降低了51.31%。综上所述，本文提出的LMD-SVD 方法的降噪结果优于单一LMD方法。

表2 两种方法降噪结果统计

3 结 语

本文在LMD方法的基础上引入了SVD方法，构建了LMD-SVD降噪方法，得到的结论为：

1）LMD-SVD 降噪方法的降噪流程为：①利用LMD 方法对GNSS 测站坐标时间序列进行自适应分解，并通过CMSE 局部极小值确定高低频分量分界点；②利用SVD方法对包含部分有用信息的高频分量进行降噪，提取高频分量中有用信息；③重构低频分量、余量以及降噪后高频分量。

2）根据奇异值差分准则，SVD 方法可以自适应选择重构奇异值个数，实现高频分量的有效重构与降噪，由于趋势项通常为低频分量，使用奇异值差分准则确定高频分量重构奇异值个数可有效避免趋势项对奇异值个数选取的影响。

3）相较于单一LMD方法，LMD-SVD降噪方法能更加准确地提取原始时间序列中的有用信息。通过对比5 个IGS 测站U 方向坐标时间序列降噪结果发现，本文方法的信噪比、相关系数均明显提高，均方根误差明显降低，表现出更好的降噪性能。