跑道型线圈板料电磁成形磁场分布的调控
唐天宇 黄亮 徐佳辉 孙怡然 周巍

摘要 :為有效调控跑道型线圈电磁成形过程中合金板料的变形行为,采用实验 模拟与理论计算的方法揭示了板料与线圈装配的相对位置对电磁力、电流密度、变形速度和成形高度的影响规律,推导出线圈中心面空间磁感强度的工程计算模型。随着板料装配时偏置量的增大,电磁成形试样变形区的最大高度差逐渐减小,试样由“内低外高”转变为“外高内低”;电磁力密度峰值从板料内侧向中心移动。偏置量为2.5~3.0 mm时,两侧高度差存在最小值;偏置量为3.0 mm时,板料的横向变形速度趋近于0,电磁力沿板料中心轴对称分布。基于跑道型线圈磁感强度工程模型推导了磁感强度对称中心区位置与线圈直段半长、匝间距、中心距及板料装配间隙的关系,确定最佳偏置量为2.2~3.9 mm。该结果与模拟实验结果相符合,证实了模型的可靠性。
关键词 :电磁成形;2219铝合金;跑道型线圈;磁场调控
中图分类号 :TG391
DOI:10.3969/j.issn.1004-132X.2024.02.018
开放科学(资源服务)标识码(OSID):
Regulation for Magnetic Field Distribution of Sheet Metal Electromagnetic
Forming with Track Coil
TANG Tianyu 1,2 HUANG Liang 1,2 XU Jiahui 1,2 SUN Yiran 1,2 ZHOU Wei 1,2
1.School of Materials Science and Engineering,Huazhong University of Science and Technology,
Wuhan,430074
2.State Key Laboratory of Materials Processing and Die & Mould Technology,Huazhong
University of Science and Technology,Wuhan,430074
Abstract : In order to effectively regulating the deformation behavior of aluminum alloy sheet in electromagnetic forming processes of track coil, the influences of the relative position of the sheet metal and the coil assembly on the electromagnetic force, current density, deformation velocity and forming height were revealed by experimental-simulation and theoretical calculation. An engineering calculation model of the magnetic induction intensity in central plane of the coil was derived. With the increase of the offset in sheet assembly, the maximum height difference of the deformation zone of the electromagnetic forming specimen gradually decreases, and the specimen changes from “low inside and high outside” to “high outside and low inside”. The peak electromagnetic force density moves from the inside of the sheet metal to the center. When the offset amount is as 2.5~3.0 mm, there is a minimum value for the height difference between the two sides. When the offset is as 3.0 mm, the lateral deformation speed of the sheet metal tends to be 0, and the electromagnetic force is axisymmetrically distributed along the center of the sheet. Based on the engineering model of the magnetic induction intensity of the track coils, the relationship among the position of the symmetrical center region of magnetic inductance and the half length of the straight section of the coil, the turn spacing, the center distance the sheet assembly clearance was deduced, and the optimal offset is as 2.2~3.9 mm. This results are consistent with the simulation experimental ones and confirm the reliability of the model.
Key words : electromagnetic forming; 2219 aluminum alloy; track coil; magnetic field regulation
0 引言
当前,轻质合金室温下难成形的特性,以及传统冲压工艺中易出现的拉裂、起皱等缺陷极大限制了铝合金等轻质板材在精密制造领域的应用 [1-2] 。电磁成形技术作为一种高速成形技术,利用脉冲电流在线圈周围产生的瞬变磁场使导电工件表面产生感应电流,将产生的电磁力代替传统机械力来驱动金属板材进行高速成形。相较于传统的成形工艺,电磁成形工艺具有成形快、精度高、可提高金属材料的室温加工性 等一系列优势 [3-6] 。由于电磁成形过程的复杂性,电磁场在材料微观结构中的作用原理及电磁力的柔性控制加载等基础性问题尚未完全解决,其中,电磁体积力对材料高速率变形中的流动行为及性能影响是首先需要解决的一个问题。成形目标及材料不一导致目前未归纳出统一规律,制约了电磁成形技术的工程应用与发展 [7-9] 。
为揭示电磁成形过程中材料塑变流动的规律,许多学者通过电磁成形基础实验研究了材料高应变率下的宏 微观特性。跑道型线圈因其作用区域广、输入能量低、线圈服役寿命长等特点而被广泛使用 [10] 。SU等 [11] 对2219-O铝合金板料进行了电磁成形与电磁间接高速变形的实验,通过分析成形载荷变化历程及应变率历程,证实了惯性效应是高速变形中提高材料成形性的主要原因。徐佳辉等 [12-13] 采用跑道型线圈对2195铝合金进行脉冲电磁处理,发现电磁脉冲处理后的预拉伸试样内部位错密度降低、分布均匀性得到改善。肖昂等 [14-15] 通过跑道型线圈对比了不同初始状态下的1060铝合金的电磁成形性能,发现加工硬化态材料的成形性能提升比退火态的更为显著。XU等 [16-17] 利用跑道型线圈对AZ31镁合金薄板进行电磁拉伸实验发现,相比于准静态拉伸,镁合金板材在脉冲磁场作用下的成形极限得到加强,且试样放置位置影响其最终的成形对称性。CUI等 [18] 基于顺序耦合仿真和实验,分析了跑道型线圈与板料位置关系不同时的电磁力与电流密度的分布规律,通过实验调试初步确定了宽度方向成形均匀时的最佳板料位置。
通过分析上述研究可知,跑道型线圈在脉冲磁场作用下的材料高速率变形过程中发挥了重要作用,但由于跑道型线圈结构的特殊性,缺乏深入研究线圈的磁场分布特性及结构对材料变形行为的影响。有学者通过解析法和数值分析方法建立了螺线管线圈和平板螺旋線圈的磁场及电磁力的分布公式,并通过实验进行了验证 [19-22] 。基于跑道型线圈的电磁成形中,目前仅通过实验试错法调整跑道型线圈结构及位置来控制板料电磁成形中变形的均匀性。然而线圈 工件结构发生变化必须重新调试,这大大限制了跑道型线圈在电磁成形基础实验中的效率及在其他领域的应用。
据此,本文基于电磁成形实验和数值模拟分析,通过改变跑道型线圈和板料的相对位置来控制板材变形过程,得到变形均匀的电磁成形件;根据跑道型线圈结构特征,建立工程简化模型,并基于楞次定律和电磁感应理论, 推导了跑道型线圈中心平面空间磁感强度的计算模型。该模型的预测结果与实验结果相吻合,揭示了线圈结构对感应磁场对称中心区位置的影响规律。
1 材料与方法
1.1 实验材料
电磁成形所用材料为2219-O(退火态),跑道型线圈由T2紫铜绕制,电磁成形所用模具材料为45钢,表1、表2所示分别为材料成分的质量分数与力学性能参数。电磁成形、单向拉伸试验所用试样的厚度为1.5 mm和2.0 mm,试样长度方向与板料轧制方向(RD)一致。在室温下进行2219-O铝合金的单向成形实验,得到图1所示的真应力应变曲线。电磁成形实验所用板料尺寸如图2所示。
1.2 设备与工装
电磁成形实验的设备型号为HMF-30/213-150,设备参数如表3所示。为确保电磁成形过程中板料达到一定变形量且不发生断裂,根据预实验结果,最终选择电容器组为8模块(106.5 μF),在放电电压10 kV的条件下进行实验。
针对电磁成形设计的工装模型内部结构如图3a所示,线圈采用环氧树脂板封装来保证强度,铝合金板料利用定位销定位,并通过垫片来约束其变形范围。图3b展示了电磁成形模具整体装配后的效果,通过销钉定位板料后,利用螺栓紧固上下模板。为便于调整线圈位置,环氧板上开孔留有一定余量与螺栓形成间隙配合。
1.3 有限元模型建立
基于跑道型线圈的铝合金电磁成形是高速率成形,其数值计算涉及电磁场与结构场的耦合求解。笔者采用LS-DYNA数值模拟软件对铝合金电磁成形过程进行模拟,采用顺序耦合法求解模型,以确保在每个时间步迭代过程中都考虑时间和结构变形对工件表面电磁力的影响。
为提高模拟精度及计算效率,只保留约束板料的部件,建立图4所示的有限元模型。为便于后文分析,将板料下表面中心定义为Q点,将跑道型线圈右侧上表面中心定义为P点,各结构的尺寸见表3,所有结构的尺寸若无特别说明, 在后续理论计算中保持不变。板料在电磁成形过程中的应变速率为准静态条件下的几十万倍,因此,本文采用考虑应变率的 Cowper-Symbols 本构模型 [23] :
σ=σ e [1+( ε · p )] h (1)
式中,σ e 为单向拉伸试验获得的准静态流动应力;p、h为应变率相关系数,p=6500 s -1 ,h=0.25 [24] 。
为确保模型的准确性,参考ZHU等 [25] 的实验方法测得相同工况下的放电系统电容、电感与电阻,计算目标放电电压下的电流并将其输入到模型。跑道型线圈通过环氧树脂封装,因此设置为刚体,认为其不发生变形。
1.4 数值模型验证
图5为用于数值模型验证的装置示意图,在相同放电参数及结构参数下,开展数值模拟与电磁成形实验。对比实验和模拟的工件变形区中心截面轮廓的成形高度,以测量值和模拟值的平均相对误差为评判标准,分析数值模型的合理性。电磁成形放电实验主要包括两个过程,首先,闭合充电回路开关S 2,充电电源对电容器充电到预设电压;然后,断开开关S 2,闭合放电回路开关S 1,电容器通过线圈在空间产生瞬变电磁场,实现对板料的成形。如图6所示,模拟值与测量值的平均相对误差为3.66%(低于5%),在可接受范围内,证实所建立的数值模型具有可靠性。
2 结果分析与讨论
2.1 线圈 板料平面相对位置的影响
板料在电磁成形过程中的变形主要受空间电磁力影响,通过调节板料与线圈的相对位置可直接改变板料周围电磁力的分布,得到不同的成形结果。为探究线圈位置对电磁成形后试样整体均匀性的影响,模拟板料与跑道型线圈在的不同偏置量 Δ(X轴正向) 处的电磁成形,得到板料变形区的位移,如图7所示。
如图7a所示,板料偏置量为0即线圈单侧中心与板料中心对齐时,电磁成形区域产生非对称变形,板料外侧(远离线圈中心一侧)的变形量明显大于内侧,且两侧变形的最大位移差出现在变形区中部。由图7b、图7c可知,随着板料偏置量的增大,板料两侧的高度差减小,板料变形更均匀。这是由于跑道型线圈在单侧空间中产生的磁场分布不均匀,导致靠近线圈中心区域的磁场强度显著下降。平板螺旋线圈实验也观测到同样的现象,即板料只在靠近线圈外侧时才能获得均匀分布的电磁力 [26] 。偏置量 Δ =3 mm的模拟结果呈现出对称的变形。
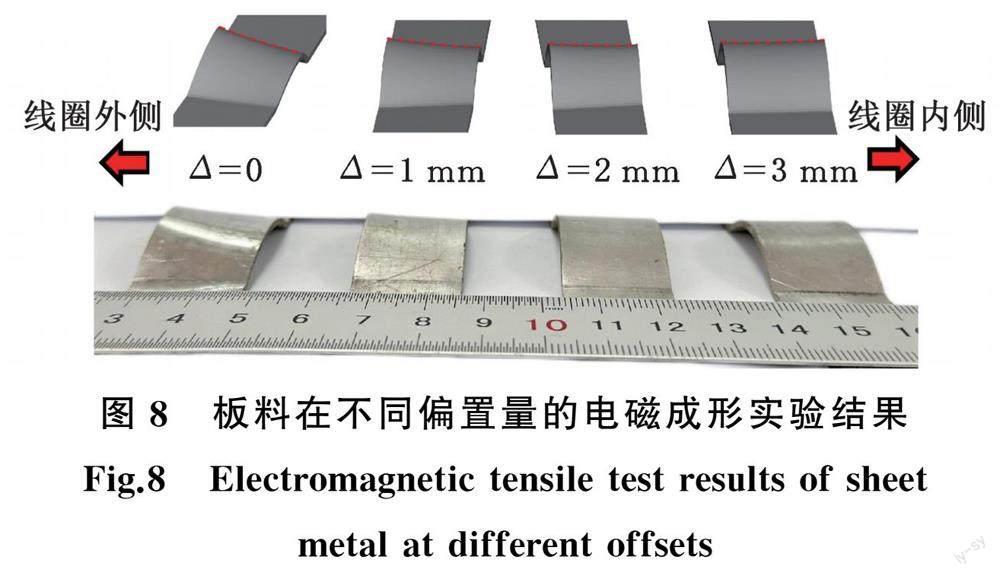
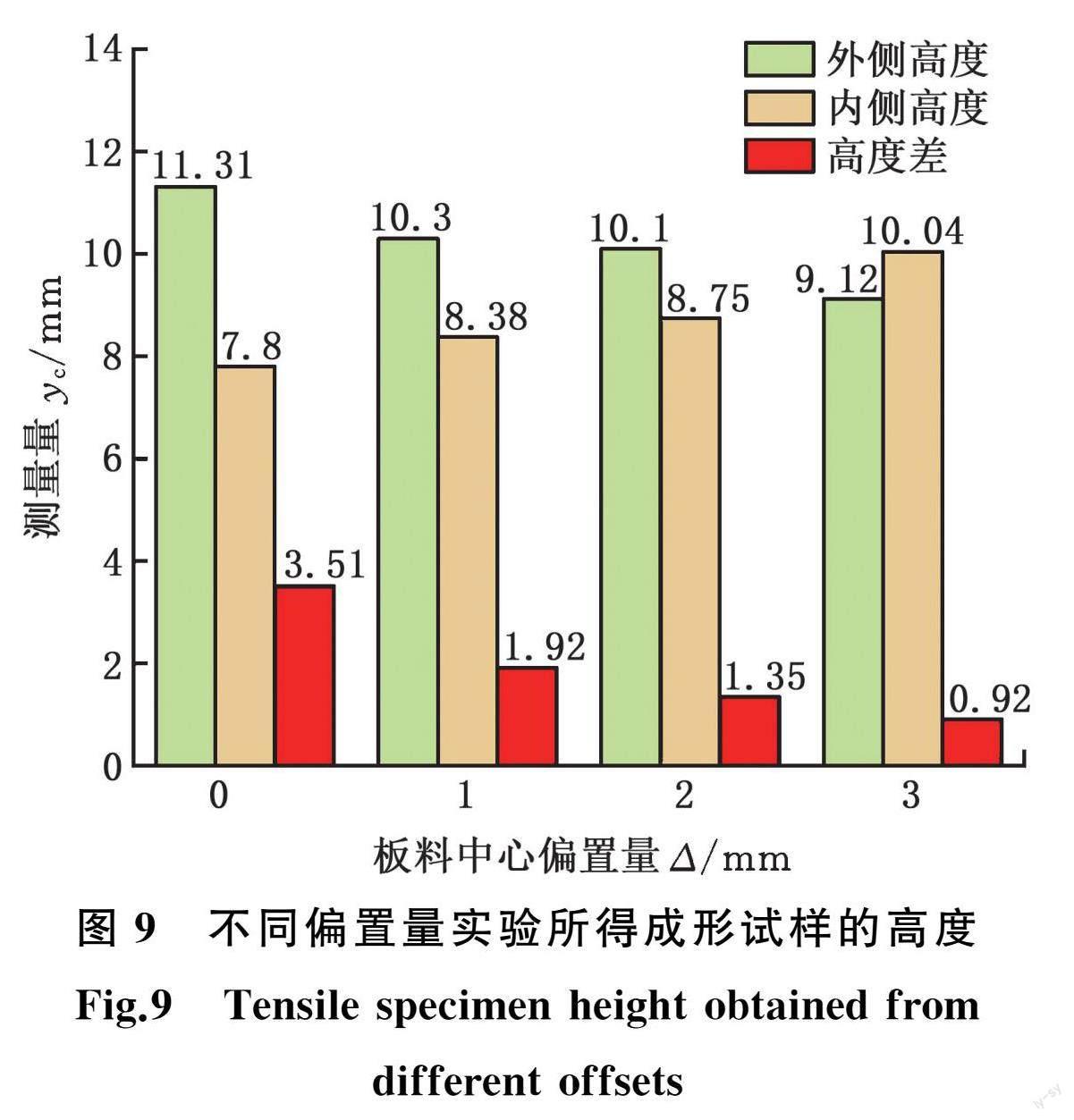
图8展示了电磁成形实验得到的试样,实验结果与仿真规律一致,进一步说明线圈与板料的相对位置影响板料变形的对称性。不同偏置量下试样中部两侧的高度差如图9所示,随着板料偏置量的增大,高度差逐渐减小;偏置量 Δ =3 mm 时,试样由“外侧高、内侧低”转变为“内侧高、外侧低”, 这说明板料偏置量 Δ 在2 mm到3 mm之间存在一个可令电磁成形两侧高度相同试样的临界值。
2.2 板料电磁力空间分布特性
电磁成形过程中,变形区电磁力的分布形式直接决定了板料的变形行为。为进一步探究线圈与板料的相对位置对电磁力分布的影响,在成形变形初期,以板料中心 Q 為原点,提取板料变形区下表面各单元在垂直板料方向上的电磁力密度,如图10所示。
根据图10b中的电磁力分布可知,跑道型线圈与板料未发生偏置时,板料表面电磁力密度未出现峰值区域,且电磁力密度从线圈中心侧沿着板料宽度负方向不断增大,但 x <-5 mm范围内的电磁力密度增幅变小。从图10c~图10e中的电磁力分布可知,电磁力密度在板料长度方向上的分布较为均匀,在宽度方向上的波动较大;板料偏置量 Δ ≥1 mm时,板料变形区域在某一宽度距离存在电磁力峰值,且该峰值点位置不断向板料中心靠拢;偏置量 Δ =3 mm时,电磁力密度沿着板料宽度中心大致呈对称分布,且板料内侧边缘的电磁力密度略大于外侧,这与实验中检测到试样中部“内侧高、外侧低”的现象相符。
电磁成形过程中,材料受到的电磁力大小不仅受磁感强度影响,还与自身感应电流相关。如图11所示,由于感应电流的边缘效应,电流在靠近板料外侧边缘处 “聚集”,对电磁力起到正贡献。电流密度在外侧的聚集抵消了部分磁场沿线圈外侧衰减时对电磁力的负贡献,这解释了图10b中的电磁力未出现峰值点的原因。图10c、图10d也有同样的规律,即在靠近板料宽度两侧处,电磁力出现骤升或衰减变缓等现象,这与图11b、图11c中的电流密度分布相符。
板料在宽度方向上受到的横向电磁力也会影响变形行为,而板料的变形速度和位移大小能很好地反映电磁力的分布。板料宽度方向上的速度分布如图12所示,偏置量 Δ =0时,板料获得较大的横向速度(指向线圈内侧);随着偏置量的增大,速度减小,偏置量 Δ =2 mm时,板料外侧出现反向速度分量; Δ =3 mm时,板料横向变形速度骤降,且呈现出一定的对称性。这说明小偏置量下的电磁力在横向上的矢量和不为0,且偏置量 Δ 在3 mm附近存在一个临界值,使电磁力在横向上达到平衡。图13中的位移曲线进一步证实,板料在横向电磁力作用下产生沿板料内侧的横向位移,且随着偏置量的增大,位移量逐渐减小,偏置量 Δ = 3 mm 时,横向位移趋近于0。综合上述分析,通过改变线圈与板料的相对位置可有效调控电磁成形过程中的材料变形;板料偏置量 Δ =3 mm时,可得变形对称的电磁成形试样。
2.3 跑道型线圈磁感强度数学模型
2.3.1 工程简化模型
为揭示电磁成形实验中板料出现非对称变形的原因,分析了宽度方向上不同偏置量处磁感强度的分布特性;提出了与线圈结构及工装位置相关的磁感强度计算模型,并对模型的可靠性进行了验证。
矩形截面的导线绕制方便且能保证较高的线圈强度,为便于分析跑道型线圈在电磁成形中的磁感强度空间分布特性,对矩形截面跑道型线圈结构及内部电流进行简化,简化的计算模型如图14所示。对跑道型线圈磁感强度的计算模型作三点假设:①忽略线圈放电过程中的能量损耗及电流聚集效应,即各匝线圈中各截面的电流大小相等且均匀分布;②只计算线圈体外部的空间磁感强度,将各匝线圈中的体电流简化为过截面形心的线电流;③跑道型线圈的直弯比(弯曲段长度与直段长度的比值)不超过0.2,根据毕 萨定理 [27] ,忽略线圈弯曲段电流对磁场影响。
2.3.2 磁场模型推导
基于上述简化模型可得,跑道型线圈空间中某点的磁感强度可等效为多条有限长的平行直导线在该点空间磁场的累加。同时,由电磁学理论易知,峰值磁感强度出现在线圈直段中心处的平面(该平面法向与电流流向相同)。因此,本文磁场模型以中心平面为基准对空间个点磁感应强度进行推导。首先,建立图15所示的磁场坐标系模型,推导任意点E(x i,y i)处单根直导线在其中心面上任意一点 O(x 0,y 0)产生的磁感应强度。
结合右手定则和毕 萨定理 [27] ,可得2 m长直导线中心面空间上任意一点O的磁感应强度:
B i= Iμ 0 2 π R m R 2+m 2 (2)
R 2=(x 0-x i) 2+(y 0-y i) 2 (3)
式中,B i为单根导线在O点产生的总磁感强度;i为直导线编号,i=1,2,3,…,10;I为通电电流;m为线圈直道段半长;μ 0为真空磁导率;R为导线中心处E到激发点O的距离。
将总磁感强度分别按图15沿线圈长度和宽度方向进行分解,并联立式(2)、式(3)可得
B r i =B i sin θ= Iμ 0|y 0-y 1| 2 π R 2 m R 2+m 2
B n i =B i cos θ= Iμ 0|x 0-x 1| 2 π R 2 m R 2+m 2 (4)
式中,B r i 、B n i 分别为O点线圈宽度和高度方向的磁场分量;θ为EO与参考X轴的夹角,θ∈(0 ° ,90 ° ]。
对跑道线圈而言,板料变形区域位于跑道线圈直道中间段,变形区长度相对跑道线圈直道段较短,所以在线圈长度方向上可以近似认为磁场强度不变,磁场强度变化集中在宽度方向,图11所示的电流密度分布结果具有该特点。因此本模型推导的公式针对板料在X方向即线圈宽度方向上变化的计算。
在单根直导线磁感强度模型的基础上,通过叠加原理,并根据图14所示的几何模型位置关系,计算多组平行直导线中心面空间上任意点O的磁感应强度:
B O=∑ 10 i=1 B i=∑ 10 i=1 Iμ 0 2 π R 2 m R 2+m 2
B r O =∑ 10 i=1 B r i =∑ 10 i=1 Iμ 0|y 0-y 1| 2 π R 2 m R 2+m 2
B n O =∑ 10 i=1 B n i =∑ 10 i=1 Iμ 0|x 0-x 1| 2 π R 2 m R 2+m 2 (5)
式中,B O、B r O 、B n O 分别为点O的总磁感强度,以及磁感强度在宽度方向和高度方向的分量。
O点与金属板料下表面中心重合时,可得到如下几何关系:
y 0-y i=k/2+δ i=1,2,…,10 (6)
x 0-x i=
W±Δ+qS i=1,2,…,5;q=2,3,…,6
qS±Δ i=6,7,…,10;q=0,1,2 (7)
式中,W为跑道型线圈中心距;k、S分别为线圈截面高度和宽度。
联立式(5)~式(7)可得板材下表面中心处的磁感强度, 且板料下表面的磁感强度主要取决于跑道型线圈各结构的尺寸及线圈和板料的间隙。
2.3.3 磁场中心偏置量计算
理想条件下,要在电磁成形过程中实现板料的均匀变形,需让电磁力沿板料下表面的几何中心对称分布。较高的放电频率下,可忽略磁渗透,则磁压力与磁场之间关系式可以简化为 [27]
P= B 2 2μ 0 (8)
式中,P为产生的磁压力;B为空间磁感应强度。
由式(8)可知,板料所受电磁力P与磁感应强度B的平方成正比。寻找磁场对称中心区间,确定板材中心位置的最佳偏置量Δ c 。跑道型线圈空间磁场公式涉及的变量过多,难以通过简化推导来确定中心点偏置量的解析表达式。为进一步探究不同因素对对称中心区位置的影响规律,结合式(5),通过控制变量法, 利用 MATLAB 軟件编写相应的计算程序,采用散点取值计算磁感应强度分量,得到磁场对称中心的偏置量范围,以该范围内的偏置量中值为磁场对称的偏置量,绘出不同因素下磁场对称中心的偏置量,如图16所示。
由图16可知,在放电条件一定的情况下,电磁成形过程中, 空间磁感强度对称中心的位置主要取决于线圈的中心距、匝间距、线圈与板料之间的装配高度差。其他条件一定的情况下,线圈中心距增大时,磁场对称中心区的偏置量不断减小;中心距超过30 mm 时,继续增加中心距离对对称中心区位置的影响较小。跑道型线圈直道段的电流方向相反,磁场对称中心点在直道段半宽靠外侧的位置。中心距增大时,两侧直段线圈间的相互干扰减小,磁场对称中心区向线圈心部偏移。由图16 b 可知线圈直道段半长对对称中心区位置几乎无影响。根据线圈环氧树脂最小封装厚度及导线规格,通常有k>2 mm ,δ>2 mm ,因此δ+k/2> 3 mm , 根据图16 c 、图16 d 可知线圈的匝间距和高度差与磁场对称中心区偏置量近似线性相关。
实际应用中,综合上述变化规律,可将各因素对对称中心区偏置量的影响归纳成工程关系模型,其中,中心距对对称中心区偏置量影响为衰减指数型:
Δ c =w 0+w 1 exp (- W w 2 ) (9)
线圈直道段半长视为无影响,线圈的匝间距与对称中心区偏置量为正相关线性:
Δ c =s 0+s 1S (10)
高度差与对称中心区偏置量为正相关线性:
Δ c =D 0+D 1(δ+ k 2 ) (11)
式(9)~式(11)中的常量w 0=0.991 58 mm ,w 1=5.353 37 mm ,w 2=28.175 32 mm ,s 0=-1.528 57 mm ,s 1=1.035 71 mm ,D 0=2.332 14 mm ,D 1=0.217 86 mm 。圖17所示的对称中心区偏置量的预测结果与计算值的拟合效果较好,图17 a ~ 图17 c 的相关系数依次为0.999 21、0.991 56、 0.975 05。
将跑道型线圈及板料的实验参数代入式(6),计算板料中心处的磁感强度,如图18所示。磁感强度对称的偏置量Δ c ∈(2.2 mm , 3.9 mm ),与实验及模拟的结果基本吻合。偏置量在中心对称区间外时,板料在成形初期无法获得对称的磁感应强度,导致表面产生的电磁力不对称。随板料中心偏离对称中心区距离的增大,磁感应强度在高度方向的分量线性增加,感应电流产生的横向电磁力使得板料中心进一步远离磁场中心对称区,加剧板料变形过程中电磁力分布的不均匀性。数值模拟与电磁实验说明本文的空间磁感应强度计算模型在跑道型线圈电磁成形过程中具有应用价值,可通过计算实现对电磁力的调控,最终实现对板料变形的控制。
3 结论
(1)为得到变形对称的电磁成形试样,根据跑道型线圈的特点,设计了线圈与板料相对位置可调的电磁成形模具,并建立了跑道型线圈电磁成形的有限元模型。在相同放电条件下,实验结果与模拟结果基本一致,平均相对误差为3.66 % ,有限元模型可靠。
(2)电磁成形模拟与实验结果表明,通过改变板料与线圈的相对位置,可实现对电磁力分布的调控,改变板料变形。随着偏置量的增大,板料的横向位移减小,成形试样两侧高度差减小;偏置量Δ=3 mm 时,试样外高内低,板料表面的电磁力对称分布。综合分析表明,Δ∈(2.5 mm , 3.0 mm )时,存在一个可电磁成形对称试样的最佳偏置量。
(3)建立了电磁成形过程中的跑道型线圈的空间磁感强度工程模型,推导了线圈中心面上任意位置的磁感应强度与线圈的直段半长、匝间距、中心距、板料装配间隙的关系;基于模型计算成功推出磁感强度对称的中心区间。此时的板料中心偏置点位置为2.2 mm ~3.9 mm ,这与模拟及实验结果相符合,证实了该工程模型的适用性。
参考文献 :
[1] JIN Y, YU H. Enhanced Formability and Hardness of AA2195-T6 during Electromagnetic Forming[J]. Journal of Alloys and Compounds, 2022, 890:161891.
[2] 金延野,于海平.板材电磁成形技术研究进展[J].精密成形工程,2021,13(5):1-9.
JIN Yanye, YU Haiping. Research Development of Electromagnetic Forming(EMF) Technology in Sheet Metal[J]. Journal of Netshape Forming Engineering, 2021, 13(5):1-9.
[3] 谢冰鑫,黄亮,黄攀,等.铝合金板料电磁翻边全流程工艺研究[J].中国机械工程,2021,32(2):220-226.
XIE Binxin, HUANG Liang, HUANG Pan, et al. Research on Whole Process Route of Electromagnetic Flanging of Aluminum Alloy Sheets[J]. China Mechanical Engineering, 2021, 32(2):220-226.
[4] 徐佳辉,黄亮,李建军,等. 基于集磁器的电磁冲裁工艺的设计与模拟[J].中国机械工程,2020,31(11):1368-1377.
XU Jiahui, HUANG Liang, LI Jianjun, et al. Design and Stimulation of Electromagnetic Blanking Processes Based on Field Shaper[J]. China Mechanical Engineering, 2020, 31(11):1368-1377.
[5] LI J, LI L, WAN M, et al. Innovation Applications of Electromagnetic Forming and Its Fundamental Problems[J]. Procedia Manufacturing, 2018, 15:14-30.
[6] PSYK V, RISCH D, KINSEY B L, et al. Electromagnetic Forming—a Review[J]. Journal of Materials Processing Technology, 2011, 211(5):787-829.
[7] 李云峰,孙向阳,宋燕利,等.电磁脉冲处理技术研究现状及其展望[J].材料科学与工艺,2022,30(4):11-24.
LI Yunfeng, SUN Xiangyang, SONG Yanli, et al. Research Status and Prospects of Electromagnetic Pulse Treatment Technology[J]. Materials Science and Technology, 2022, 30(4):11-24.
[8] 李亮.我國多时空脉冲强磁场成形制造基础研究进展[J].中国基础科学,2016,18(4):25-35.
LI Liang. Basic Research Progress of Multi-time Pulse High Magnetic Field Forming Manufacturing in China[J]. China Basic Science, 2016, 18(4):25-35.
[9] 邱立,李彦涛,苏攀,等.电磁成形中电磁技术问题研究进展[J].电工技术学报,2019,34(11):2247-2259.
QIU Li, LI Yantao, SU Pan, et al. Research on Electromagnetic Problems in Electromagnetic Forming Process[J]. Transactions of China Electrotechnical Society, 2019, 34(11):2247-2259.
[10] 李昊桦,张梅富,姜爔,等.AA1060–DP600板材电磁脉冲连接工艺研究[J].精密成形工程,2022,14(12): 146-152.
LI Haohua, ZHANG Meifu, Jiang Xi, et al. Experimental Study on Electromagnetic Pulse Joining Technology of AA1060-DP600 Sheet[J]. Journal of Netshape Forming Engineering, 2022, 14(12):146-152.
[11] SU H, HUANG L, LI J, et al. Formability of AA 2219-O sheet under Quasi-static, Electromagnetic Dynamic, and Mechanical Dynamic Tensile Loadings[J]. Journal of Materials Science & Technology, 2021, 70:125-135.
[12] 徐佳辉,黄亮,谢冰鑫,等.铝锂合金电磁形变复合热处理工艺研究[J].机械工程学报,2022,58(16):58-67.
XU Jiahui, HUANG Liang, XIE Bingxin, et al. Study on Electromagnetic Deformation Combined with Heat Treatment Process of Al-Li Alloy[J]. China Mechanical Engineering, 2022, 58(16):58-67.
[13] XU J, HUANG L, XU Y, et al. Effect of Pulsed Electromagnetic Field Treatment on Dislocation Evolution and Subsequent Artificial Aging Behavior of 2195 Al-Li Alloy[J]. Materials Characterization, 2022, 187:111872.
[14] 肖昂,颜子钦,崔晓辉,等.不同热处理状态铝合金在电磁成形条件下的成形性研究[J].精密成形工程,2021,13(5):58-65.
XIAO Ang, YAN Ziqin, CUI Xiaohui, et al. Formability of Aluminum Alloy with Different Heat Treatment States under Electromagnetic Forming Condition[J]. Journal of Netshape Forming Engineering, 2021, 13(5):58-65.
[15] XIAO A, YAN Z, HUANG C, et al. Effect of Initial State on Formability of AA1060 Alloy under Quasi-static and Electromagnetic Forming[J]. Journal of Materials Research and Technology, 2022, 19:2781-2793.
[16] XU J R, YU H P, LI C F. An Experiment on Magnetic Pulse Uniaxial Tension of AZ31 Magnesium Alloy Sheet at Room Temperature[J]. Journal of Materials Engineering and Performance, 2013, 22:1179-1185.
[17] XU J R, LIN Q Q, CUI J J, et al. Formability of Magnetic Pulse Uniaxial Tension of AZ31 Magnesium Alloy Sheet[J]. The International Journal of Advanced Manufacturing Technology, 2014, 72:665-676.
[18] CUI X, ZHANG Z, YU H, et al. Dynamic Uniform Deformation for Electromagnetic Uniaxial Tension[J]. Metals, 2019, 9(4):425.
[19] 黃尚宇,常志华,田贞武,等.管坯电磁成形电磁力解析[J].中国机械工程,2000,11(10):98-101.
HUANG Shangyu, CHANG Zhihua, TIAN Zhenwu, et al. Electromagnetic Shaping of Tube Blank Electromagnetic Force Analysis[J]. China Mechanical Engineering, 2000, 11(10):98-101.
[20] 黄尚宇,常志华,王立峰,等.板坯电磁成形载荷计算方法及分布特性[J].中国有色金属学报,1998(3):76-81.
HUANG Shangyu, CHANG Zhihua, WANG Lifeng, et al. The Calculation Method and Distribution Characteristics of Electromagnetic Forming Load of Slab[J]. The Chinese Journal of Nonferrous Metals, 1998(3):98-101.
[21] 初红艳,费仁元,吴海波,等.椭圆线圈在平板电磁成形中的应用研究[J].锻压技术,2002(5):38-41.
CHU Hongyan, FEI Renyuan, WU Haibo, et al. Application Research of Elliptic Working Coil Used in Sheet Metal Electromagnetic Forming[J]. Forming and Stamping Technology, 2002 (5):38-41.
[22] BATYGIN Y, BARBASHOVA M, SABOKAR O, et al. Magnetic Pulsed Pressure for Forming Inner Angles in Sheet Metals[M]∥Electromagnetic Metal Forming for Advanced Processing Technologies. Berlin:Springer, 2018:5-34.
[23] TIAN Y, HUANG L, MA H, et al. Establishment and Comparison of Four Constitutive Models of 5A02 Aluminum Alloy in High-velocity Forming Process[J]. Materials & Design (1980-2015), 2014, 54:587-597.
[24] ZHANG Q, HUANG L, LI J, et al. Investigation of Dynamic Deformation Behaviour of Large-size Sheet Metal Parts under Local Lorentz Force[J]. Journal of Materials Processing Technology, 2019, 265:20-33.
[25] ZHU H, HUANG L, LI J, et al. Strengthening Mechanism in Laser-welded 2219 Aluminum Alloy under the Cooperative Effects of Aging Treatment and Pulsed Electromagnetic Loadings[J]. Materials Science and Engineering:A, 2018, 714:124-139.
[26] UNGER J, STIEMER M, SVENDSEN B, et al. Multifield Modeling of Electromagnetic Metal Forming Processes[J]. Journal of Materials Processing Technology, 2006, 177(1/3):270-273.
[27] 雷银照.轴对称线圈磁场计算[M].北京:中国计量出版社,1991:106-109.
LEI Yinzhao. Calculation of Magnetic Fields of Axial Symmetry Coils[M]. Beijing:China Measurement Press, 1991:106-109.
( 编辑 张 洋 )
作者简介 :
唐天宇 ,男,1999年生,硕士研究生。研究方向为磁脉冲成形理论及工艺。E-mail:tangtianyu@hust.edu.cn。
黄 亮 (通信作者),男,1981年生,教授、博士研究生导师。研究方向为多时空脉冲强磁场下高强铝合金成形理论和技术。发表论文200余篇。E-mail:Huangliang@hust.edu.cn。

