面向河道治理工程质量评价的模糊综合评判法研究

涂志俊

(湖北路达胜工程技术咨询有限公司，湖北 武汉 430015)

1 模糊综合评价体系构建

1.1 河道治理工程模糊综合评价体系

FAHP是在模糊数学的基础上构建的一种评价方法，可以根据隶属度将定性的评判转化为定量；FAHP评价具有将多种制约因素融合，作出整体综合性评价的特点[1]。对于河道治理工程，评价方法受人为主观因素的制约，为不同的需求服务。评价指标的多样化导致得到多个结果，不同的结果之间并没有联系，结果片面而不具备客观性[2]。因此在研究中引入FAHP构建评判体系，期望将多个评价指标综合起来作出一个整体评价，使得评价更加合理客观，为决策者提供科学的参考依据。FAHP体系建立流程如图1所示。

图1 模糊评价体系建立流程

由图1可知，FAHP体系的构建主要分为了四步，第一步选择评价指标与评价等级；第二步，构建评价矩阵；第三步，确立各指标的权重；第四步，开展模糊合成，即将选择的指标进行综合，再选择一个最佳决策作为最终评价结果[3]。

若被描述事物受到m种因素的制约，则存在因素影响集合U={u1，u2，…，um}；若每一种因素有n个评语个数，则存在因素决断集合V={v1，v2，…，vn}。然后构建评判矩阵，对每一个影响因素Ui(i=1，2，…，m)作出评价，rij为因素ui对决断等级vj(j=1，2，…，n)的隶属度，那么ui的单个因素评价集为ri=(ri1，ri2，…，rin)[4]。m个因素构建出评价矩阵R如式(1)所示。

(1)

式中：R为U到V的模糊关系。对于不同类型的指标将采用不同方法确定矩阵隶属度[5]。带有主观性的指标都含有模糊性，因此在此利用等级比重的方法满足FAHP的需求，确定隶属矩阵。在使用等级比重法时需要考虑一些问题，首先评价人数要达到指定要求，尽可能地让等级比重接近隶属度；其次，评价人员必须是专业人才，拥有相关领域的专业知识。而对于客观性更强的指标，将采用频率法来划分指标值的变化区间，再利用指标值的历史信息在不同区间出现的频率确定隶属度。每一个制约因素对评价判断的目的都有不同的作用与不同的重要程度，单独运用矩阵仍然达不到对事物评价的客观度。因此，还需考虑影响因素的权重，即各个评价指标的权重。设集合A为U中的一个模糊子集，即为权重分配集，可表示为A=(a1，a2，…，am)，其中，ai>0，且∑ai=1。

权重的赋值是重要的量度值，赋权的过程往往带有主观性，一定程度范围内的主观性也具备客观性，反映了实际情形。而当判断者出现失误时，导致带有较强的主观色彩，使得评价结果不具备参考价值。鉴于此，权重的确立可以利用数学方法，利用数学方法严密的逻辑思维对权重进行修复处理，以此去除掉决策者的主观成分，让结果更加客观合理。在此之后需要进行模糊合成，综合考虑中不同的隶属度，将其进行合成，用模糊权向量A表示，通过A可以得到整体范围内各个等级模糊子集的隶属程度[6]。B为V上的一个模糊评价子集，则B=(b1，b2，…，bn)，模糊变换公式如式(2)所示。

B=A*R

(2)

式中：*为算子符号，算子是一个容易理解、普遍运用的合成方式。在此运行过程中需要保证0≤bj<1，若出现∑bj≠1，需要将其进行归一化处理。其中bj表示被评事物的vj程度。B的主要作用是对分等级的程度进行描绘，需要对其进行处理后才能进行排序应用。此时可以利用最大隶属度方法进行处理，得到最优结果。在这个过程中，只利用了B中的最大值，为了充分利用B中的信息，需要同时考虑等级参数和B，得到结果如(3)所示。

(3)

式中：C为各等级vj的参数向量；p为等级参数评价结果，是反映B与C的综合结果。

1.2 模糊综合评价体系在质量评价中的应用

在将FAHP运用到河道治理质量评价之前，需要对河道治理工程质量评价指标进行详细的了解，在充分了解分析河道治理影响指标的基础上才能建立FAHP体系。目前河道治理工程质量评价结构如图2所示。

图2 河道治理工程质量评价结构

由图2可知，质量评价分为四个模块，分别是单元工程模块、单位工程模块、分部工程模块与工程项目模块[7]。通过这四个模块依次的质量分析评价，将工程项目质量分为优良与合格这两个层次。单元工程的质量评价标准是，每一个单元达到优良的标准，单元工程即可被评为优良。分部工程的评价标准是在单元工程与中间产品质量评价的基础上开展的，若中间产品质量均合格，且砂浆质量达到优良水平；单元工程质量均被评定为合格，且70%以上达到优良水平。此时分部工程才会得到优良的评价。单位工程的质量评价标准是在分部工程的基础上开展的，若要评定优良，主要需要满足这些条件：首先，70%以上分部工程得到优良评价且全部合格，现场无重大事故发生；其次>85%的外观质量得分率；最后资料要齐全，相关合同与资料分析结果符合国家与行业标准。工程项目的质量评定是在单位工程的基础上，若要评定优良，需满足70%以上单位工程达到优良水平，且全部合格；还需全部工程的相关合同与资料分析结果符合国家与行业标准[8]。水利工程的外观质量评价如图3所示。

图3 水利工程外观质量评价内容

由图3可知，每一个项目有四个评价等级，分别是100.0%、90.0%～99.9%、70.0%～89.9%、0～69.9%。一级的得分率为100.0%，二级的得分率为90.0%，三级的得分率为70.0%，四级的得分率为0%。按照这四个等级确定水利工程项目的得分率，各个项目的分值是项目的标准分与该项目得分百分率的乘积，再将各个项目的分值加起来为此工程的实得分。项目的应得分是各个项目标准分值之和，工程的外观评价得分率是实得分与应得分的商乘以100%。当外观得分率>70.0%时视为合格，>85.0%视为优良。对于每一项项目的等级判断要慎重处理，如混凝土表缺陷得分率计算时，具当缺陷>5.0%时，可给出四级评定，即得分率为0%，若无任何缺陷时得分率为100.0%在此过程中，可以对某处不符合标准的地方进行返修，直至达标。当遇到不能进行返修的情况，考虑此处缺陷对实际功能的影响，若无影响可对等级评定进行降级，若影响实际效用则降到第四级。

外观质量评价的得分来自项目检测的数据，与检测人员给出的叙述性结论。检测数据是指对工程的外部结构尺寸、轴线结构与建基面高度等，通过在工程现场采集而来。由于在工程的施工现场有一部分项目内容是无法用数据进行测量，更无法用数据进行量化评价[9]。因此，检测人员采取现场检测的方式，对需要评价的项目给出专业的叙述性描述结论，并根据描述的具体内容划分等级，作出等级评价。在对评价指标体系进行了解过程后，引入FAHP，FAHP是结合了定性与定量分析，综合了评价指标，让质量分析结果变得更加客观合理。图4是FAHP的具体运用流程。

图4 FAHP的应用流程

如图4所示，首先确定质量评价体系的基础数据集，数据集是评价的基础，充分运用收集数据，更能反映过程的实际状况，作出理性合理的评价，然后确定质量评价体系中各个指标的权重占比。在此之后对数据进行分析，构建河道工程外观质量评价模型与河道工程单元工程质量评价模型，在FAHP的基础上构建模型，通过评价体系的构建、评价集的形成、权重的确立与模糊矩阵的构建，对河道工程质量进行综合评价。

2 FAHP应用结果分析

此次研究对面向河道治理工程质量的FAHP模型进行性能测试。为了避免不同设备造成的试验误差，研究在相同的试验环境下进行，其操作系统为Windows 10 Home，RAM为20 GB，CPU为Inter(R) Core(TM) i5-10210U，内存为16 G。测试采用Matlab 2020搭建基于FAHP的河道治理工程质量评价模型。为了得到最优的初始种群规模，研究将种群规模分别设置为20、40、60、80，得到的训练结果如表1所示。

表1 在不同种群规模下的训练结果

由表1可知，随着初始种群规模的增加，收敛时间逐渐增加，误差先减少再增加。在初始种群规模为40时，收敛时间相对较短，误差最小，因此在后面的试验中将种群规模设置为40，交叉概率设置为0.5。为了验证试验模型的优越性，在此引入自适应变异遗传-反向传播(AGA-BP)算法的评价模型进行性能的对比分析，评价模型在训练时，经过多次迭代后，AGA-BP评价模型与FAHP模型的评价值与真实值的对比如图5所示。

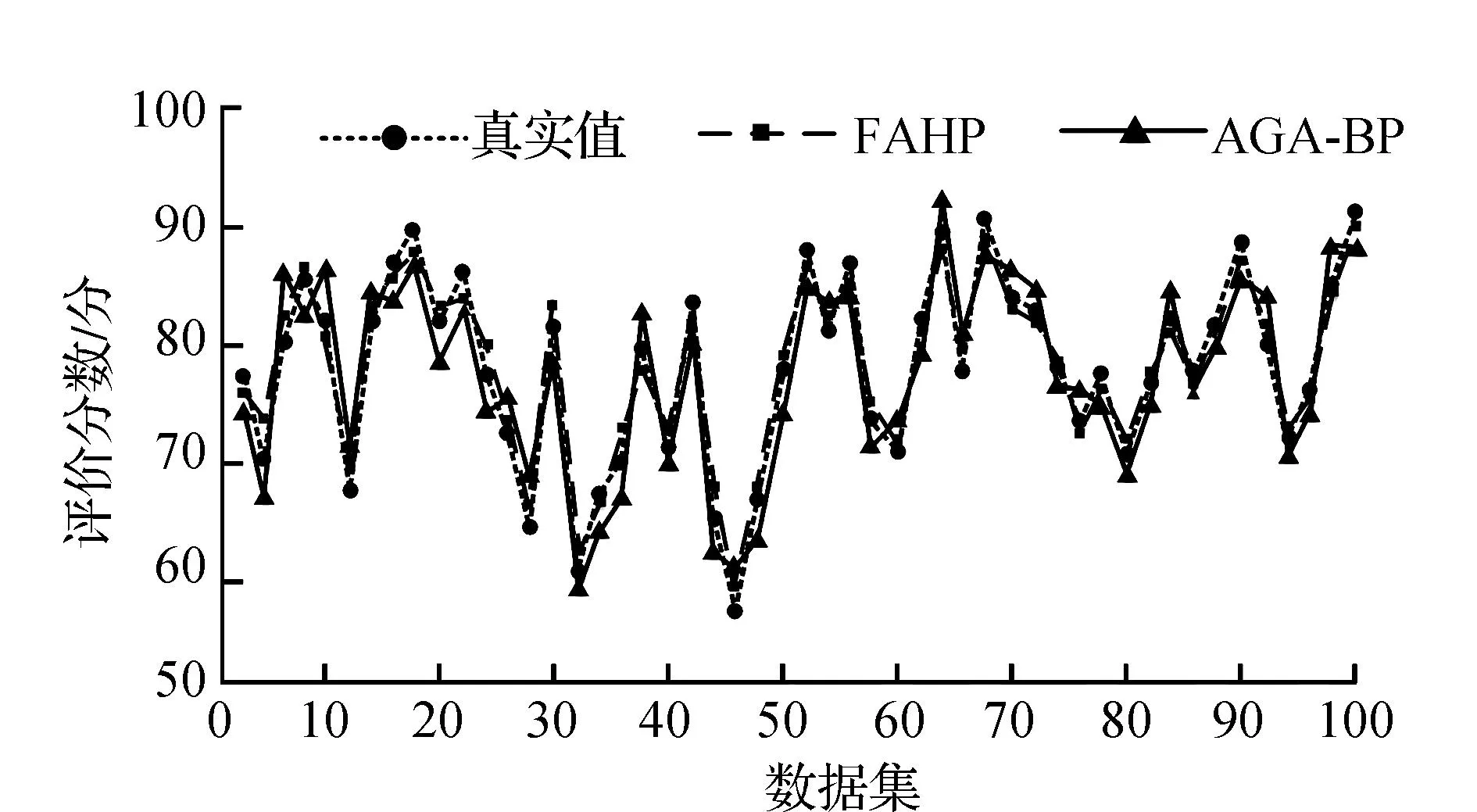
图5 不同数据集的评估值与实际值之间的对比

由图5可知，100组评价真实值平均得分为76.84分；FAHP模型输出的评价得分平均为75.98分；AGA-BP评价模型输出的评价得分平均为69.27分。FAHP模型真实值与评估值仅存在1.25%的差异，而AGA-BP评价模型真实值与评估值差异为8.36%。FAHP模型评价分数最大值为91.16分，出现在64组，其评价分数最小值为61.23分，出现在46组；AGA-BP评价模型评价分数最大值为93.12分，出现在62组，其评价分数最小值为67.83分，出现在46组。FAHP评价模型准确度高于AGA-BP评价模型7.11%。整体而言，FAHP模型评估值更接近真实值，并且FAHP每一组数据的测试结果更稳定，验证了FAHP模型的准确性和稳定性。为了进一步对FAHP模型AGA-BP评价模型的差异进行对比，此次研究随机选取了60组样本，其期望输出和模型实际输出的相对误差如图6所示。

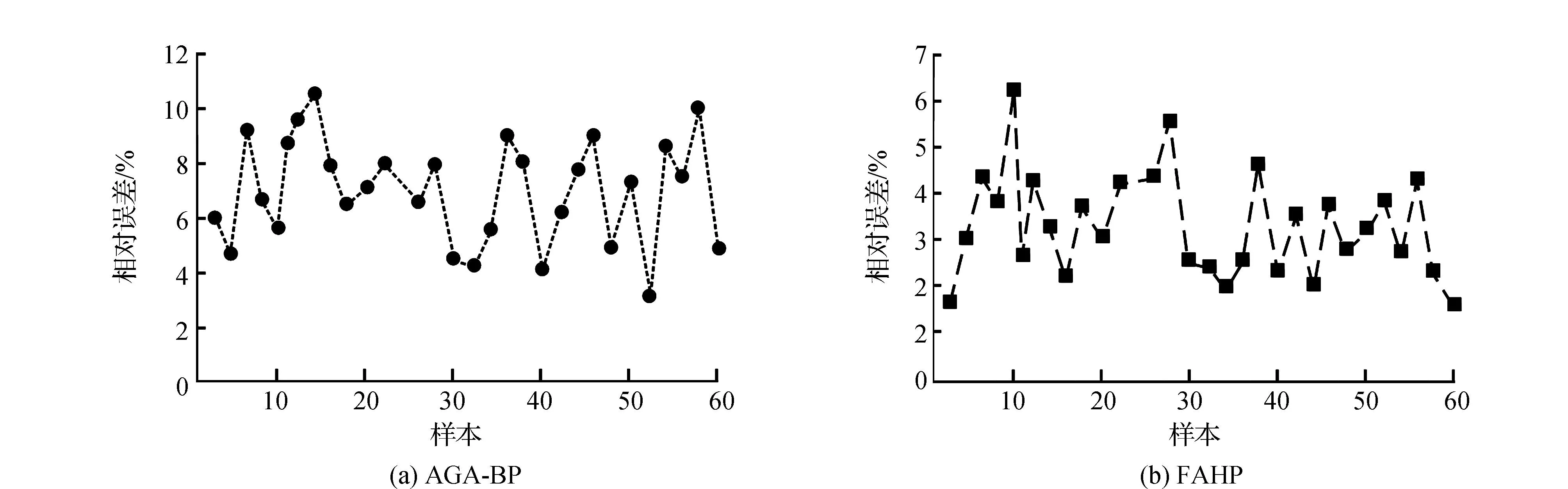
图6 模型的预期输出和实际输出之间的相对误差结果

如图6所示，图6(a)为AGA-BP评价模型期望输出值与实际输出值的相对误差，最低误差为2.56%，出现在52号样本中，最高误差为11.29%，出现在16号样本中，相对误差上下限差值为8.73%，60组样本的平均相对误差为7.36%。图6(b)为FAHP模型期望输出值与实际输出值的相对误差，最低误差为1.48%，出现在2号样本中，最高误差为6.12%，出现在12号样本中，相对误差上下限差值为4.64%，60组样本的平均相对误差为3.56%。整体而言，此次研究提出的FAHP模型期望输出与实际输出的相对误差更低，较AGA-BP评价模型降低了3.80%，并且FAHP模型相对误差上下差值更小，更稳定。为了验证了FAHP模型在河道治理工程评价上的适用性，将该模型运用到武汉某竣工河道中。将运用FAHP模型得到的结果与实际评价结果进行对比，测试其准确率。此竣工河道外观得分率如表2所示，与混凝土的强度检测数据结果，建立矩阵，确认模糊隶属度，得到工程项目的评价结果。

表2 河道治理工程外观质量评分

如表2所示，根据外观质量评判标准，对河道治理工程的外观质量进行评价，评价者根据实际情况对工程项目的外观质量指标进行打分，外观质量评级指标主要有外部尺寸、排水、砌缝、表明平整度、轮廓线、曲面与平面的连接，由表2可知，实际得分为75.2，应得分为83，计算得到外观质量的得分率为90.6%。满足外观质量得分率达到85%以上的条件，此河道外观质量被评定为优良。利用FAHP模型得到外观质量评价向量与混凝土强度质量评价向量，根据隶属度得到该工程质量属于良。此河道实际的质量评价结果也是良，与此次研究结果一致，验证了FAHP评价模型的准确度，进一步证明了FAHP评价模型在河道治理工程评价中运用有一定的适用性。

3 结 论

面对河流污染日渐加剧的严峻形势，河道治理任务越来越重，河道治理工程的质量评价是其中重要的一环。为了更加准确科学的对工程质量进行评价，此次研究选择FAHP对河道治理工程质量中的各个质量指标进行综合考虑评价。模型性能测试实验结果显示，FAHP评价模型准确度高于AGA-BP评价模型7.11%，证明此次研究提出模型性能更佳。将FAHP评价模型运用到实际的河道工程中，结果显示此工程质量为良，与工程实际的质量评价结果一致，准确度高，适合应用在河道治理工程的质量评价中。但是模糊评价法仍存在不足之处，其最大隶属度的选择方式可能会导致结果失真，后续工作将对此作出改进。