基于多特征融合的MIMO-OFDM系统单-混信号调制识别算法
邹 涵, 张天骐, 马焜然, 杨宗方
(重庆邮电大学通信与信息工程学院, 重庆 400065)
0 引 言
随着通信技术的发展,频谱资源愈发短缺,认知无线电因可以节约频谱而得到重视。其中,多输入多输出正交频分复用(multiple-input multiple-output orthogonal frequency division multiplexing, MIMO-OFDM)技术通过正交多载波进行传输,能够有效节约频带资源,因此在第三方通信中,正交频分复用(orthogonal frequency division multiplexing, OFDM)等多载波技术得到广泛应用。然而,信号调制类型识别的成功与否在一定程度上决定了信号盲处理质量的高低[1-2],因此多载波信号盲调制识别问题具有研究价值。同时,在通信系统中,通信双方可在同一频带上发送对称混合信号,从而节约带宽资源,提高系统吞吐能力。综上所述,研究MIMO-OFDM单-混信号的盲调制识别方法具有重大意义[3]。
自动调制分类(automatic modulation classification, AMC)技术用于识别接收端未知信号的调制格式[4]。AMC方法通常可以分为两大类:第一种是基于似然(likelihood-based, LB)的方法。LB方法主要通过比较不同调制信号的似然函数来实现调制识别,其中似然函数分为3类:混合似然校验比[5]、平均似然校验比[6]和广义似然校验比[7]。但LB方法需要先验信息,且计算量较大,不适用于盲处理。相比之下,第二种基于特征的方法适用范围更广,基于特征的方法在设计合理的情况下能够识别更多类型的调制信号并且计算复杂度较低,因此基于特征的识别方法得到了广泛应用。基于特征的方法是指首先从信号提取合理特征,然后再进行分类识别。其中提取的特征主要有以下几种,如高阶累积量[8-9]、星座图[10-11]、时频分析[12-13]、信号瞬时特性[14]等。分类判决是指利用支持向量机、决策树[15]等完成分类任务。近年来,人工智能等技术进一步成熟,其优异的数据处理能力引起广泛关注。2016年,O’Shea提出以时域同相正交分量作为输入端、以卷积神经网络 (convolutional neural network, CNN)作为训练网络的识别算法[16],但仅用CNN提取特征的效果不太明显。文献[17]利用双向长短记忆网络实现6种信号的盲调制识别。文献[11]使用基于深度学习的AMC方法,将星座图累积与同相正交分量作为输入特征实现低信噪比条件下的OFDM信号调制识别。文献[15]根据信道矩阵和相关矩阵的特点,提取特征参数,能有效识别正交空时分组码与非正交空时分组码。文献[18]将深度神经网络与多任务学习框架结合,实现OFDM信号信噪比盲估计与调制识别。但以上算法都只针对单信号,混合信号的调制识别算法都集中在单载波系统中,如杨洪娟等[19]等提出基于高阶累积量和星座图聚类算法的调制识别算法,该算法能够对卫星单-混信号进行有效识别。因此,针对多载波系统的调制识别算法还需要继续进行研究。
本文提出一种基于多特征融合和决策融合相结合的MIMO-OFDM单-混信号盲调制识别算法。该算法采用四次方谱、循环谱与高阶累积量作为输入,采用多端特征融合网络进行特征提取,合并决策融合作为判决输出。首先,估计发射天线数目,本文采用最小描述长度准则(minimum description length, MDL)进行估计,利用特征矩阵的联合近似对角化(joint approximate diagonalization of eigenvalue matrix, JADE)算法[1]恢复发送信号;然后,根据恢复信号计算出循环谱、四次方谱与高阶累积量,其中循环谱与四次方谱作为第一端输入,高阶累积量作为第二端输入;其次,搭建多端特征融合网络提取高维特征,再利用识别网络得到每一支路输出;最后,采用决策融合[19]方式对每条支路输出进行融合判决,得到最终输出结果,实现二进制相移键控(binary phase shift keying, BPSK)单混信号、正交相移键控(quadrature phase shift keying, BPSK)单混信号、八进制相移键控(8 phase shift keying, 8PSK)和16路正交振幅调制(16-ary quadrature amplitude modulation, 16QAM)单混信号共7种信号的调制类型分类。
1 系统模型与数据集的构造
1.1 系统模型
在本文中,MIMO-OFDM系统考虑为:发射天线、接收天线数分别为Nt,Nr,且两者满足Nt 图1 MIMO-OFDM系统模型Fig.1 MIMO-OFDM system model 发送信号考虑为对称混合信号。通常,对称混合信号具有相同的调制类型、调制速率,以及相同或细微差别的幅度、频率、频偏与时延等。由于OFDM信号抗时延性能优秀,因此接收信号可不考虑时延。在不考虑频偏的前提下,第nt根发送天线的发送信号可表示为 snt(t)= exp-j2πfcTsg(t-lTs) (1) (2) 信道考虑为平坦衰落信道,第nt根发送天线和第nr根接收天线间的信道转移系数为hntnr(t),则第nr根接收天线接收信号可表示为 (3) 因此,接收信号可以通过矩阵形式表示为 (4) 在MIMO-OFDM系统中,由于MIMO信道作用,接收信号原有的统计特性会被破坏[1]。因此,需要消除信道影响,恢复发送信号。信号恢复分为盲估计与半盲估计,在非协作通信中往往不能获得先验知识,为了切合实际,本文采用盲估计。文献[1]在MIMO系统框架下比较了常用的3种盲源分离算法。其中,JADE算法在更小数据输入时恢复效果更好,因此本文采用JADE算法进行发送信号的恢复。具体地,信号恢复分为3个阶段:① 采用MDL算法求解得到发送端天线数量;② 对接收端接收到的天线做白化处理以降低信号维数;③ 使用JADE算法根据估计的天线数目与白化后信号,恢复信号子载波。其中,天线数目估计步骤如下所示: (1) 求接收信号y(t)自相关矩阵: Ry=E[y(t)yH(t)] (5) (2) 对自相关Ry做特征分解,得到Nr个特征值并按降序排列; (3)估计发射天线数Nt: (6) 式中:L表示单根天线符号数;λi为第i个特征值。 为降低JADE算法复杂度,提高算法性能,对接收信号进行白化操作。 (1) 根据自相关矩阵Ry进行特征分解,将前Nt个大的特征值按降序排列组成矩阵D,且每一特征值对应的特征向量组成矩阵F; V=B2FH (7) 最终,信号可表示为 q(t)=V·Y(t) (8) 经白化处理后,信号维数从Nr×1 降低为Nt×1,降低了后续计算量。 在获得发射天线数与数据白化处理之后,便可使用JADE算法恢复发送信号。恢复步骤如下: (1) 求得白化矩阵q(t)的四阶累积量矩阵,记为C; (2) 对C进行奇异值分解,取模最大的Nt个特征值φi与其特征矩阵Ui构成矩阵A={φi,Ui|1≤i≤Nt}; (3) 对A作近似对角化,得到分离矩阵X,恢复信号可表示为 (9) 1.3.1 循环谱 对于混合的平稳随机信号,有: s(t)=s1(t)+s2(t) (10) s(t)循环自相关函数为 (11) 由于s1(t)与s2(t)为相互独立序列,因此有E[s1(t)s2(t)]=0。故混合信号s(t)的循环自相关函数可表示为 Rs(t,τ)=Rs1(t,τ)+Rs2(t,τ) (12) 式中:τ表示时延。 对Rs(t,τ)经离散傅里叶变换(discrete Fourier transform, DFT)后可得混合信号s(t)的循环自相关函数: (13) 对Rs(t,τ)作DFT得到循环谱密度函数: (14) 式中:f为信号频率;α为循环频率。 (15) 故带噪声的混合信号的循环谱可以表示为 (16) 本文采用时域平滑算法对循环谱进行估计[20]。以BPSK和16QAM为例,图2给出了BPSK单信号、BPSK混合信号、16QAM单信号、16QAM混合信号三位循环谱图。从循环谱可以看出,单信号与混合信号在谱峰数上有明显区别。图3分别给出信噪比为10 dB、子载波调制方式分别为MPSK(M=2、4、8),16QAM单信号与混合信号循环谱图与在f=0处的切片图。从图3可以看出,不同单信号谱峰特征在相同信噪比下存在差异,单信号与混合信号的谱峰宽度与谱峰数也有明显差异。因此循环谱在f=0处的切片可以作为特征1输入神经网络,以进行训练。 图2 部分调制信号的循环谱图Fig.2 Cyclic spectrum diagram of partially modulation signals 图3 各调制信号的循环谱切片图Fig.3 Cyclic spectrum slice diagram of each modulation signals 1.3.2 四次方谱 四次方谱的定义为 (17) 图4分别给出信噪比为10 dB、子载波调制方式分别为BPSK、16QAM单信号与混合信号的四次方谱图。从图4可以明显看出,BPSK只有单个高冲击分量,16QAM除了有更多冲击分量外,在零频附近也有冲击分量。因此,四次方谱可作为第二个输入特征,对信号的调制方式进行识别。 1.3.3 高阶累积量 高阶累积量具备能表征含基带噪信号星座图分布、抑制高斯噪声等特性。虽然进行载波调制会影响信号线性关系,导致高阶累积量误差较大,但每种调制信号高阶累积量具有差异。在基带MIMO-OFDM系统中,单信号高阶累积量与混合信号高阶累积量相比有明显差异,因此选用高阶累积量作为第三特征输入。高阶累积量具体计算步骤如下: 对平稳随机信号s(t),其a阶混合矩为 Mab=E{[s(t)a-bs*(t)b]} (18) 式中:a表示为s(t)阶数;b表示为s*(t)阶数。s(t)的k阶累积量定义为 Ckx(τ1,τ2,…,τk-1)= (19) 式中:Cum表示累积量;τ1,τ2,…,τk-1表示时延。s(t)的各阶累积量可以表示为 C20=Cum(s,s)=M20 (20) C21=Cum(s,s*)=M21 (21) (22) C41=Cum(s,s,s,s*)=M41-3M21M20 (23) (24) (25) (26) 设置单-混信号幅度比值为1∶1。基带单、混信号高阶累积量理论值如表1所示。 表1 单-混信号高阶累积量理论值Table 1 Theoretical values of high-order cumulants of single-mixed signals 通过表1可知,{BPSK}、{QPSK、8PSK}与{16QAM}有明显差距,并且对{BPSK混}有C21=C42=2E2,{QPSK混、16QAM混}满足C21=2C42。因此把C21、C42作为第三、第四输入特征。 仿真信道选取为平坦衰落信道且信道系数的均值为0,方差为1。其中,考虑到OFDM信号循环谱特点,选取循环谱f=0的切片特征,结合四次方谱以及高阶累积量作为网络输入。 本文设计的MIMO-OFDM系统调制识别算法原理如图5所示。对接收信号通过恢复、计算等一系列处理得到特征值,再将特征值输入训练网络进行特征提取和决策分类,最后进行决策融合。 图5 MIMO-OFDM调制识别原理Fig.5 MIMO-OFDM modulation identification’s principle 本文采用的特征提取模块如图6中的特征提取模块部分所示。 图6 多特征融合的CNN模型Fig.6 CNN model with multi-feature fusion 其中,一维CNN(one-dimensional CNN, 1D CNN)结构由5个一维卷积层和4个平均池化层组成,如图6中1D CNN结构部分所示。 利用神经网络模型融合循环谱、四次方谱和高阶累积量,利用三者特征在不同调制方式下的差异使得算法具有更优的识别性能。其中Fil表示卷积核的个数,Ker表示卷积核的大小。Conv 1D通过卷积核与数据的卷积运算来提取高维特征,Conv 1D层输出为 (27) 随后,采用平均池化层来降低输入数据长度。平均池化层计算公式为 (28) 输入的多端数据经一维卷积层和平均池化层后得到特征数据,为了充分利用各端特征数据,需将数据进行融合操作。融合操作可以分为相加(add)和拼接(concatenate)两种方式。相加操作通过添加值来获得新特征,但可能导致原数据失真。拼接操作可以叠加多段特征,且不会损失任何信息。因此,选择拼接操作来进行特征融合。 经过特征提取与融合得到的数据通过展平层(flatten)得到一维数据并以全连接方式连接到分类器模块。分类模块如图6中分类模块部分所示,包括2个Dropout层,2个全连接层(Dense层)和1个输出层。 全连接层FC-2特征矢量可通过全连接层FC-1特征yl1求得,表示为 yl2=σ(Wl2yl1+bl2) (29) 式中:Bl2和bl2分别表示网络参数训练权重和偏置。 Dropout在训练中将部分节点置零以减少过拟合,在本文中选择rate为0.3。 输出层采用Softmax函数,Softmax函数将数据转换为1×7的概率矢量p,p=[p1,p2,…,p7],分别对应其中的调制方式。第i种调制方式的概率具体表示为 (30) (31) 本文采用随机梯度下降(stochastic gradient descent,SGD)策略来更新网络权重W和偏置b。梯度下降算法对W和b的更新公式为 (32) (33) (34) 一个batch对应的损失函数为 LBCE(θ)= (35) 针对MIMO-OFDM系统,由于受到噪声影响程度不同,每路信号恢复效果不同,所蕴含的特征表达能力也不同,因此每一路特征融合网络对每一路信号的识别精度也有所差异。为了提升最终识别精度,本文采用决策融合[21]来汇总每一路信息,这种方式有助于提升识别精度,具体如图5所示。 2.3.1 投票决策 投票决策通过每条支路信息,使用少数服从多数操作来给出最终判决结果V(x): (36) (37) 2.3.2 置信度决策 投票决策依靠每路最终判决结果,而判决结果由Softmax激活层输出p决定,因此也可以直接将每种调制类别的预测概率矢量进行累加得到最终概率密度矢量,选择概率最大的对应的调制方式作为最终调制方式。具体地,数学上可表达为 (38) (39) 本文所提出的调制识别算法流程如算法1所示。 算法 1 MIMO-OFDM系统单混信号调制识别算法预处理利用MDL算法估计出发射天线数,再通过JADE算法得到发送信号,最后根据恢复信号得到3种浅层特征:高阶累积量、四次方谱和循环谱。输入提取循环谱f=0切片,与四次方谱构成2×2 048的二维数据,从第一端输入;C21,C42也构成2×2 048的二维数据,从第二端输入。网络训练(1) 随机打乱训练样本,按每个batch有128个样本进行划分,共划分为m个batch;(2) 将m个batch输入训练网络;(3) 采用SGD方法更新网络权重W和偏置b,并保存最优模型。 本节对本文所提的MIMO-OFDM系统单-混信号调制识别算法进行仿真。本文环境考虑为基带MIMO-OFDM系统,发送天线数为3,接收天线数为5。首先,进行仿真实验并采样得到MPSK单(M=2,4,8)、MPSK混(M=2,4),以及16QAM单和16QAM混共7种信号。具体地,采样频率为100 kHz;载波频率为15 kHz[1,15];混合信号时两混合信号载频分别为15 kHz和16 kHz;码元速率为2 kbit/s;信噪比范围为0~20 dB且间隔为2 dB,按照每种信噪比下每种调制信号训练样本数为1 000条,测试样本数为500条,训练集总共包含样本数77 000条,测试集总共包含样本数38 500条。 实验 1算法性能测试。本节验证所提识别算法的性能。图7给出信噪比在4 dB、10 dB、16 dB、20 dB下的混淆矩阵。在信噪比为4 dB时,由于BPSK类信号高阶累积量与四次方谱相比其余调制信号特征差别较大,因此BPSK单、BPSK混合信号识别率达到100%,而QPSK和8PSK同为PSK类信号,其3种特征差异较小,因此这两类调制信号识别率较低。但随着信噪比升高,当信噪比为10 dB时,BPSK单、BPSK混、QPSK单、8PSK、16QAM单信号识别率达到100%,QPSK混和16QAM混识别率也达到95%以上。这是由于带通信号载波影响会导致高阶累积量在一定范围内浮动,对识别精度产生一定影响,这种影响随着信噪比提高逐渐减小。从图8可以看到,在信噪比达到12 dB时,各个信号调制识别率均达到98%及以上。 图7 不同信噪比下的混淆矩阵Fig.7 Confusion matrix under different signal-to-noise ratios 图8 各调制信号识别精度Fig.8 Recognition accuracy of various modulation signals 实验 2比较不同决策方式对模型精度的影响。本节将投票决策、置信度决策和3条支路输出作比较,识别精度为所有测试样本统计所得。观察不同决策方式对模型精确度的影响。从图9可以看出,采用多路信号决策融合的方法得到的模型比单一支路的决策模型性能更加优秀。由于QPSK单、QPSK混和8PSK信号均属于PSK类信号,因此这3种信号之间特征差异较小,易受噪声影响。另外QPSK混和16QAM混在高阶累积量上差异较小,由于信道噪声影响,容易造成两信号高阶累积量混淆,因此单一支路模型识别效果较差。相比单一支路的决策识别方法,决策融合方法克服单一支路决策中存在的由噪声引发的问题,得到的模型精度提高了5%~10%,且随着信噪比增加,噪声干扰逐渐减小,决策融合模型与单一支路模型误差逐渐减小。另外,在投票决策融合过程中,每条支路的输出判决结果会导致置信概率信息丢失,因此投票决策融合相比于置信决策融合,精度减少了2%~5%。因此,在本文仿真中,均采用置信决策融合。 图9 不同决策方式下的模型精度Fig.9 Model accuracy under different decision methods 实验 3不同算法下的对比实验。本节将本文所提调制识别算法与其他算法进行比较,识别精度为所有测试样本统计所得。文献[1]为传统调制识别方法,将高阶累积量与四次方谱最大值与次大值之比作为特征值,使用BP(back propagation)神经网络作为分类器。文献[21]将循环谱与四次方谱作为输入特征,然后利用1D CNN训练来进行调制识别。文献[22-23]提取信号同相正交分量,然后分别利用InceptionNet与ResNet来完成调制识别。 从图10可以看出,BP神经网络性能最差,一是选取特征值不足以表征各信号特征,导致识别效果较差;二是BP神经网络性能差,可能出现局部最小点。对于利用循环谱、四次方谱的1D CNN,其两特征值对混合信号特征表达能力较弱,因此对混合信号的识别精度差,其整体识别精度也受到一定影响。而利用同相正交分量作为特征值的Inception与ResNet,由序列直接提取特征值,易受噪声影响,所获得的调制识别性能略低于本文所提算法。 图10 不同算法的识别精度Fig.10 Recognition accuracy of different algorithms 本文以循环谱、四次方谱和高阶累积量作为特征,提出了针对MIMO-OFDM系统的混合信号调制识别算法。首先通过MDL估计发射天线数,再利用JADE恢复发送信号并计算每条发射支路的循环谱、四次方谱与高阶累积量。然后将循环谱与四次方谱作为第一端特征输入,将2阶累积量和4阶累积量作为第二端输入,完成对多载波系统的子载波的调制识别。最后,再利用置信决策融合方式融合每条支路结果,减少由噪声带来的误差,提高识别精度。实验结果表明,本文算法对MIMO-OFDM单-混信号盲调制识别精度较高,在信噪比为6 dB时,所提算法对各单-混信号识别精度可达90%以上。此外,该方法在应用中不需要任何先验信息,仅需从发送端对信号进行采样,适用于第三方通信等无需先验知识的通信场景。


1.2 MIMO-OFDM信号恢复
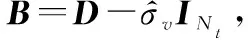
1.3 特征提取

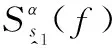




Cum[s(t),s(t+τ1),…,s(t+τk-1)]
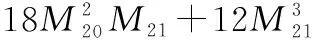

1.4 数据集构造
2 识别算法

2.1 特征提取


2.2 分类器模块


2.3 决策融合模块


2.4 算法流程

3 仿真实验及结果分析





4 结 论

