天文/惯性组合系统中重力扰动补偿方法
冷 悦, 钟 胜
(1. 华中科技大学人工智能与自动化学院, 湖北 武汉 430074; 2. 多谱信息智能处理技术全国重点实验室, 湖北 武汉 430074; 3. 华中光电技术研究所武汉光电国家研究中心, 湖北 武汉 430223)
0 引 言
现代战场环境对导航系统在强干扰、复杂电磁环境下长航时、高精度、高可靠工作的需求愈发迫切。天文导航系统能够提供误差不随时间累积的姿态和位置信息,但其易受天气条件限制[1-2],与惯性导航系统自主连续、定位误差随时间发散的特性形成强烈的互补[3]。天文/惯性组合导航系统综合了天文导航、惯性导航的技术优势,独立自主且不受外部电磁环境干扰,被广泛应用于长航时、高精度导航领域[4-6]。
天文/惯性组合导航系统的精度主要受时间精度、测星精度、惯性水平基准(本质上为惯导)精度等因素的影响[7-9],随着原子钟技术、测星传感器技术的发展,时间精度、测星精度已不再限制天文/惯性组合导航系统的极限精度。相反,惯性水平基准精度已逐步演变为制约天文/惯性组合导航精度进一步提升的关键因素。在长航时、高精度导航领域,随着惯性器件精度的不断提高,受到地形、地质影响的重力扰动成为高精度惯导的主要误差源[10-17]。相关研究表明,水平方向的重力扰动分量每增加10 mGal时,对应高精度舰载惯导的位置误差约增加130 m[18],而全球重力扰动最大可达500 mGal[19-22]。
针对重力扰动的补偿,文献[23]证明了EIGEN-6C4模型以及重力数据插值对惯导系统进行重力扰动补偿的效果相同。文献[24]利用全球定位系统(global positioning system, GPS)等辅助信息对重力扰动进行在线估计并将其引入惯导系统中。文献[25]研究了基于EIGEN-6C4重力场球谐模型的高精度惯性导航系统重力扰动补偿方法。文献[26]分析了重力扰动在高精度惯导系统中的传播特性,并提出了重力扰动补偿方法对重力场球谐模型阶数的要求。文献[27]基于2190阶EIGEN-6C4重力场球谐模型获取极区重力扰动数据,并将扰动数据补偿到极区高精度惯导系统中。文献[28]通过实际飞行试验,验证了所提出的重力扰动补偿方法可以有效提升惯导的姿态精度。综上所述,虽然国内外学者针对重力扰动对惯性导航设备的影响及补偿技术做了大量的研究,但重点都是重力扰动对惯性导航设备定位误差的直接影响,没有将重力扰动补偿技术、天文测星导航技术相结合,通过重力扰动补偿提高惯性水平基准的水平姿态精度,进而利用高精度水平姿态实现天文导航定位精度的提升。通过两种信息源的融合,有望进一步发挥重力扰动数据与天文测星数据对惯导定位误差的修正效果。
基于以上背景,本文开展天文/惯性组合系统中重力扰动补偿方法的研究,通过建立误差模型,分析重力扰动、惯性水平基准姿态测量误差与天文/惯性组合导航系统中定位误差之间的传播机理,研究重力扰动建模与修正方法,并应用于惯性水平基准的导航解算回路中,提高惯导水平姿态精度,进而提升天文/惯性组合导航系统的定位精度。最后,通过跑车试验对补偿方法的有效性进行验证。
1 惯性水平基准误差对天文导航定位误差影响的理论分析
现代天文导航组件主要以惯性导航组件作为其测星水平基准信息源。同时,天文测星导航信息又用于修正惯性导航解算信息[29-30]。天文导航组件与惯性导航组件共同构成了天文/惯性组合导航系统,其基本原理如图1所示。

图1 天文/惯性组合导航系统原理示意图Fig.1 Schematic diagram of celstial/intertial integrated navigation system
根据惯性水平基准误差方程,有
(1)
式中:φx,φy,φz分别表示惯性水平基准的姿态误差在地理坐标系下沿东向、北向、天向三轴的分量;L为惯性水平基准解算输出纬度;δL,δλ表示惯性水平基准导航解算输出的纬度误差和经度误差。在忽略惯性水平姿态误差的情况下,有

(2)
(3)
(4)
在惯性水平基准的姿态解算过程中,若由重力扰动引起0.1 mg的水平加速度测量误差,将导致20″的姿态测量常值误差,考虑舒勒振荡影响,姿态测量误差的幅值将超过40″。针对海上船载平台,虽可通过外接计程仪对舒勒振荡进行速度阻尼,但速度阻尼对舒勒振荡的抑制需要至少84.4 min(即舒拉振荡的周期[31]),对于变化较快的重力扰动存在严重响应滞后,速度阻尼对由重力扰动引起的惯性水平基准姿态误差的抑制效果较差。因此,有必要研究重力扰动的修正方法,以降低其对式(4)中水平姿态的影响。当惯性水平基准的水平姿态精度获得提高时,天文导航定位解算的理论残余误差Δ将变小,进而天文导航的定位精度得以提升。
2 天文导航重力扰动误差传播机理
2.1 重力扰动对惯性水平基准的影响机理
重力扰动主要通过惯性水平基准的比力方程体现,比力方程[31-32]如下:
(5)
式中:gn为重力矢量在地理系下的投影,导航过程使用重力矢量:
(6)
(7)
分析式(5)和式(7)可知,重力扰动引入的误差量等效为额外引入加速度计的测量误差,因此重力扰动对惯性水平基准的影响可等效为加速度计测量误差。
2.2 由重力扰动引起的姿态测量误差模型
由重力扰动对天文导航惯性水平基准的影响可等效为加速度计测量误差对惯性水平基准的影响,因此首先给出加速度计测量误差与惯性水平基准姿态测量误差之间的关系,在此基础上推导出重力扰动与惯性水平基准姿态测量误差之间的关系模型。
加速度计测量误差与惯性水平基准姿态测量误差之间的关系模型[31-33]为
(8)

同理,根据加速度计测量误差与重力扰动之间的关系模型,可直接推导出重力扰动与惯性水平基准姿态测量误差之间的关系模型为
(9)
式中:φx,Δg,φy,Δg为重力扰动引起的x轴向和y轴向水平姿态误差。
联立式(8)和式(9),重力扰动和加速度计测量误差对惯性水平基准姿态误差的综合影响模型为
(10)
式(9)为仅由重力扰动引起的惯性水平基准姿态测量误差模型,式(10)则为实际工程系统中重力扰动和加速度计测量误差综合作用引起的惯性水平基准姿态测量误差模型。
根据式(4)和式(10)可知,重力扰动与天文导航定位误差之间的关系模型为
(11)

参考EGM2008等全球重力场模型和相应垂线偏差数据[19-22],全球重力扰动在水平方向上主要在[-450,+470]mGal范围内变化,引起的姿态测量误差最大可达90″,对应的天文导航定位误差最大可达2 700 m;平均重力扰动为5 mGal,对应的天文导航定位误差约为150 m。因此,重力扰动对水平姿态测量误差的影响不可忽略,为提高天文导航精度,必须修正重力扰动的影响。
3 重力扰动修正策略
根据第2.1节的分析可知,重力扰动通过影响惯性水平基准姿态测量精度,进而影响天文/惯性组合系统的导航精度。因此,有必要研究重力扰动修正惯性水平的基准策略,实现天文/惯性组合系统的重力扰动补偿,具体的补偿流程如图2所示。

图2 改进天文/惯性组合导航算法流程图Fig.2 Flowchart of improved celestial/intertial integrated navigation algorithm
在图2中,重力扰动补偿主要作用于惯性水平基准,即在水平基准的惯性导航解算过程中,引入重力扰动数据库以及匹配重力扰动两个功能模块,在实际工程中可采用EGM2008等模型或者数字天顶仪获取重力扰动数据库,进行异常重力的匹配计算。
为了定量分析重力扰动对天文/惯性组合导航精度的影响,需要获取准确的局部重力扰动数据。因此,本文首先通过数字天顶仪测量并构建重力扰动数据库,然后在匹配重力扰动功能模块中,依次输入导航位置信息、提取重力扰动矢量和补偿重力矢量。其中,重力扰动矢量提取是重力扰动补偿的前提,具体包括构建拓扑计算图、确定数据库曲面拟合模型,以及计算当前位置点的重力扰动。
(1) 构建拓扑计算图

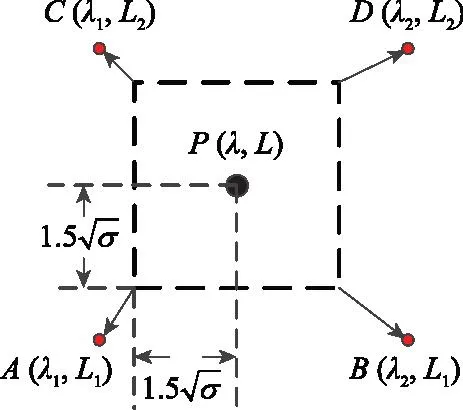
图3 重力扰动局部查询区域Fig.3 Local query area of gravity disturbance
将正方形4个顶点分别向外拓展,将重力扰动数据库中距离顶点最近的点标记为A、B、C、D。将A、B、C、D4个点继续向外扩展,得到12个点A、B、C、D、A1、B1、C1、D1、A2、B2、C2、D2,如图4所示。

图4 重力扰动提取示意图Fig.4 Schematic diagram of gravity disturbance extraction
由载体位置点、12个扩展参考点共同构成重力扰动提取拓扑计算图。12个参考点的重力扰动值已知,若载体恰好停在任意一个重力扰动参考点对应的位置,则在惯性水平基准计算中可直接补偿该重力的扰动值。若载体处于12个网格参考点之间,则需根据12个参考点,采用数据库曲面拟合的方式,推算P点的重力扰动值。
(2) 基于数据库的曲面拟合模型
为不失一般性,假设P(λ,L)位置处重力扰动值用函数G(λ,L)表示。构造以位置P为自变量的三阶二维曲面拟合方程如下:
G(λ,L)=aλ3+bL3+cλ2L+dλL2+eλ2+fL2+
gλL+hλ+jL+i
(12)
式中:a、b、c、d、e、f、g、h、j、i为待拟合曲面参数。根据已知12个重力扰动参考点G1(·),G2(·),…,G12(·)及其经纬度,形成12个联合方程,有:

(13)
将该方程组转换为向量及其求解形式:
(14)
式中:X即为通过最小二乘待求的三阶二维曲面参数,用于对P点重力扰动值进行拟合。
(3) 计算当前位置点重力扰动
将P点位置信息(λins,Lins),代入多项式式(12),可得P点处的重力扰动测量值(λins,Lins)为
G(λins,Lins)=a(λins)3+b(Lins)3+c(λins)2(Lins)+
d(λins)(Lins)2+e(λins)2+f(Lins)2+g(λins)(Lins)+
h(λins)+j(Lins)+i
(15)
式中:G(λins,Lins)表示gn一个方向上的重力扰动,与12个点同方向的重力扰动参考值有关。
本文基于东向和北向各12个重力扰动参考值,经两次匹配分别获取两组曲面参数,拟合出P点的重力扰动,分别表示为η、ξ。惯性水平基准比力方程所用重力矢量为gn,则重力扰动修正方程为
(16)
其中,天向方向重力扰动分量对惯性水平基准姿态影响较小,且数字天顶仪无法获取该方向的参考值,因此本文不做补偿。
4 试验验证
为了验证本文提出的天文/惯性组合导航系统中重力扰动补偿方法的性能,进行了跑车试验,并与无重力扰动修正条件下天文/惯性组合导航系统定位精度进行对比,以验证重力扰动修正对天文/惯性组合导航定位精度的提升效果。
4.1 试验设计
跑车试验地点选在重力扰动较大的湖北襄阳市南漳县山区,在试验车中放置了1套天文/惯性组合导航设备;1套水平定位精度优于10 cm的差分卫星导航接收机并将其作为导航位置基准;1套重力扰动测量精度优于0.1″的数字天顶仪(1″约为4.9 mGal),用作制备当地重力数据库;1套数据录取装置,用作同步存储天文测星原始数据、惯性水平基准原始陀螺加表数据、重力扰动数据以及卫星导航位置基准数据。
其中,天文/惯性组合导航系统中惯性水平基准采用50型激光单轴调制惯导(陀螺精度为0.01°/h),纯惯性定位精度约为2 nmile/(8 h)。天文导航组件采用短波红外测星传感器,具备昼夜测星能力,测星精度优于8″。
(1) 跑车行驶轨迹
试验车按照南漳县市政路线行驶,基于卫星地图绘制出跑车行驶轨迹,如图5所示。

图5 试验跑车行驶路线Fig.5 Driving route of test sports car
在正式的跑车评估算法性能试验前,先借助数字天顶仪沿着跑车路线测量当地的重力扰动,以提前备制跑车路线区域的重力数据库。
(2) 重力扰动测量结果
在进行正式算法评估试验时,跑车累计行驶20 h,跑车沿线多数区域重力扰动在10″左右,如图6所示。

图6 高精度数字天顶仪重力扰动测量曲线Fig.6 Gravity disturbance measurement curve of high-precision digital zenith instrument
当天文/惯性组合导航设备受到天气条件限制无法获取恒星观测数据时,设备此时主要进行纯惯性导航;当天气条件允许观星时,设备此时主要利用天文观测数据修正惯性水平基准的定位误差。
4.2 试验结果
跑车试验结束后,基于存储的天文测星原始数据、惯性水平基准原始陀螺加表数据、重力扰动数据以及卫星导航位置基准数据,解算输出纯惯性导航、天文/惯性组合导航重力扰动修正前以及修正后的定位误差曲线,如图7所示,其局部放大图如图8所示。

图7 纯惯性、天文/惯性组合、天文/惯性组合+重力扰动修正的导航误差对比Fig.7 Comparison of navigation errors among intertial, celestial/intertial, celestial/intertial with gravity disturbance correction

图8 重力扰动修正前后天文/惯性组合导航误差放大图Fig.8 Enlargement diagram of celestial/intertial integrated navigation error before and after gravity disturbance correction
当气象环境满足天文导航测星条件时(如图7中的10 h、12 h、14 h、18 h),天文/惯性组合导航系统的位置误差显著降低,此时再结合重力扰动修正,天文/惯性组合导航系统的定位误差幅值总体变小、舒拉振荡幅度变小,表1为扰动修正误差对比。

表1 纯惯性、天文/惯性组合、天文/惯性组合+重力扰动修正的误差对比Table 1 Comparison of navigation errors among intertial, celestial/intertial, celestial/intertial with gravity disturbance correction n mile
从理论上分析,天文导航主要对惯性导航位置地球振荡误差、积累误差有修正作用,对舒拉振荡误差影响较小。天文导航修正惯导后的位置残余误差主要由惯导水平姿态误差决定。在重力异常区域,水平姿态受重力扰动影响而变大,增加重力扰动修正,可提高惯性水平姿态精度,进而提升天文/惯性组合系统的定位精度。上述实验结果与理论分析结果相符合,具体说明如下:
(1) 在图7中对比粗实线与虚线可以看到,在使用重力扰动修正前,天文/惯性组合导航相对纯惯性导航,虽然位置误差得到了修正,但舒拉振荡误差的幅值并没有出现明显变化。因此,经过多次修正后,舒拉振荡误差逐渐成为其位置误差的主要来源。
(2) 在图7中对比细实线与虚线可以看到,在使用重力扰动修正后,不仅位置误差得到了修正,并且舒拉振荡得到很好的抑制,定位精度得到了明显提高。
(3) 在图8中对比细实线与虚线可以看到,当第18 h天文测星有效时,天文/惯性组合导航系统的定位误差从2.7 n mile抑制到0.24 n mile,重力扰动修正后定位误差舒勒振荡幅值从1.6 n mile抑制到0.5 n mile。修正重力扰动后,定位误差的振荡幅值以及系统总体定位误差均大幅下降。
5 结 论
本文分析了重力扰动通过影响惯性水平基准姿态进而影响天文导航定位精度的误差传播机理,提出了天文/惯性组合导航中重力扰动建模与补偿方法。首先,基于惯性导航推算出载体位置点,在重力扰动数据库中搜索并匹配当地的重力扰动参数,然后在惯性导航解算回路中补偿重力扰动,提升惯性水平姿态精度。跑车试验结果表明,本文提出的重力扰动修正方法可以降低重力扰动对天文/惯性组合导航定位精度的影响,天文/惯性组合导航系统定位误差的振荡幅值由1.6 n mile降低至0.5 n mile,定位精度显著提升。

