基于MDCFT与水平集的高海情弹载雷达成像检测方法
周 利, 胡杰民, 付连庆, 凌三力
(1. 西南电子技术研究所, 四川 成都 610036; 2. 浙江理工大学信息学院, 浙江 杭州 310018)
0 引 言
主动雷达探测具有高分辨、全天时、全天候和可以直接观察等优点,是弹载平台对海面目标探测采用的主要体制之一,在实际应用中占有相当重要的地位。弹载雷达成像的距离向分辨能力通过发射宽频带信号获得,横向分辨力是通过积累时间内雷达视线相对目标的转动获得。时至今日,海战环境日益复杂,特别是高海情探测环境,给弹载雷达精确制导带来了巨大挑战。主要表现在:① 高海情条件下,海浪的剧烈涌动会造成舰船三维摆动,由三维摆动引起的多普勒频率具有随机性和不稳定性,使得长时间的相参积累不一定能达到提高舰船多普勒分辨力的效果。② 高海情下破碎浪的存在会导致大量海尖峰出现在成像平面内,从而引入大量虚检,增加弹载雷达探测识别的不确定性。因此,开展针对弹载平台高海情下的目标成像检测方法研究,对于反舰导弹全天候作战能力的提升具有重要的支撑作用。
由于高海情下实测试验的高风险性以及应用方向的敏感性,目前公开报道高海情下海面目标成像检测研究成果的文献寥寥无几。从可查阅的文献资料来看,现有高海情探测的研究成果主要集中于海杂波与舰船电磁回波模拟以及成像等方向。
文献[1]研究了破碎波对海面电磁散射的影响,将破碎波散射近似为劈结构散射,然后用射线追踪方法计算电磁特性数据。这种方法具有较好的稳定性且计算效率较高,其缺点是没有考虑海面与舰船以及海面各面片之间的耦合效应。文献[2]对目标与复杂地海面复合电磁散射建模的研究现状进行了综述,并指出了可供参考的研究方向。
在高海情下舰船目标成像研究方面,文献[2-4]对复杂运动目标的成像研究进行了综述;文献[5-8]研究了基于成像时间段的高海情舰船逆合成孔径雷达(inverse synthetic aperture radar, ISAR)成像方法。文献[6]将平均多普勒展宽最大的时间段作为最优成像时间段;文献[7]和文献[8]分别根据角速度矢量和海面探测先验信息(海况等级、舰船速度以及风速等)确定成像平面稳定、分辨率较高的时间段,这类方法的优点是只需要传统距离多普勒(range-Doppler, RD)算法就能完成目标成像,缺点是只选取多普勒近似定值的时间段,成像积累时间受限。针对时间选取方法的缺陷,文献[9-10]将方位慢时间回波建模为高阶相位信号,并分别基于时间-调频率分布积分以及乘积型高阶匹配相位变换的思路,利用Clean方法逐个获得目标散射点。由于Clean方法存在迭代过程,对于散射点较多的舰船目标,这类方法的计算量很大。文献[11]提出基于三阶改进离散chirp傅里叶变换(modified discrete chirp Fourier transform, MDCFT)的ISAR成像算法,算法实现过程不涉及Clean方法的迭代步骤且可通过快速傅里叶变换(fast Fourier transform, FFT)进行快速运算,运算效率较高。
在海面目标检测方面,文献[12-14]针对海面微弱目标研究了基于特征的检测方法,文献[15]对基于特征的检测方法进行了总结。然而对于弹载高海情应用背景而言,其面临的主要技术难点是舰船能量的散焦以及由海尖峰导致的虚警问题。文献[16]利用改进小波变换处理结合高低帽滤波与闭运算完成海面目标检测,该方法具有一定的消除海尖峰的能力,但作者没有进行进一步分析。
舰船三维摆动和海尖峰的存在是制约高海情环境弹载雷达探测性能的关键因素之一。本文面向弹载雷达高海情探测应用场景,提出一种新的舰船成像检测思路。首先,建立高海情下舰船与海杂波回波模型。针对由舰船三维转动引入的相位高次项导致的多普勒散焦问题,本文采用MDCFT算法实现高阶相位信号的相参积累;其次,提出一种基于水平集算法的舰船检测方法,初步检测目标可能存在区域;在此基础上,利用聚类算法获取每个目标的区域,提取目标特征并判决目标是否为舰船。最后,利用仿真实验与现有算法进行了比较,验证了所提算法的有效性。
1 高海情下弹载雷达回波建模
1.1 海杂波建模
目前,国内海环境模拟系统尚不具备构造大于3级海情海面的能力,高海情电磁散射特性数据主要通过仿真手段获取,高海情杂波建模并非本文主要工作,这里借鉴已有的研究成果[1]进行实现,如图1所示。海杂波模拟过程可归纳如下:首先,根据风速、风向以及海谱类型生成高海情下的海面几何模型;其次,对海面进行剖分和离散化处理,每个海面上面片的散射系数根据雷达散射截面(radar cross section, RCS)随入射角的变化规律计算[17],破碎波的存在是造成海尖峰的根本原因:通常情况下,海表面的斜率越大,越容易出现表面破碎现象,就越容易产生海尖峰。这里将海面上斜率超过设定门限的面片筛选出来。在这些面片上,回波将由后向散射系数很强的海尖峰替代,通过所有面元回波合成得到海面面元回波。
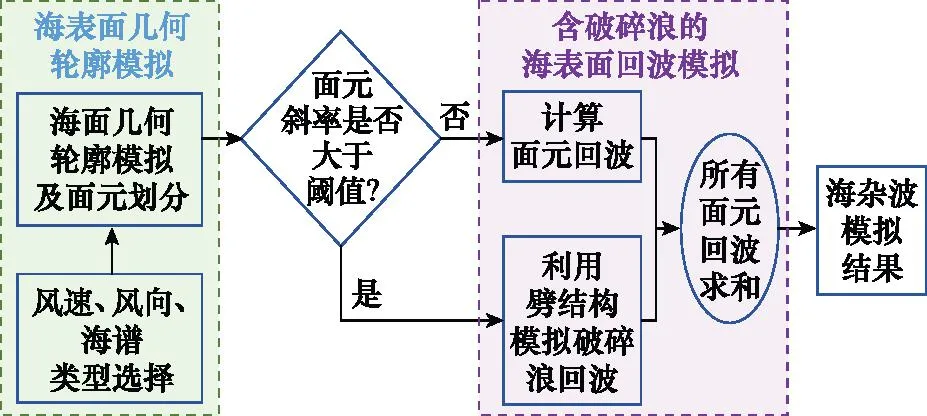
图1 高海情下的海杂波模拟流程图Fig.1 Flowchart of sea clutter simulation process with high sea conditions
采用线性滤波法并考虑风向影响建立的二维海面几何轮廓如图2所示,海面被划分为2 m×2 m的面元,每个面元的斜率分别通过计算得到,本文将斜率大于预设门限(仿真中将门限设为最大门限的0.9倍)的面元设定为破碎波所在的位置,如图2(b)所示,该位置回波用海尖峰替代。含破碎波海面的总散射场可以表示为
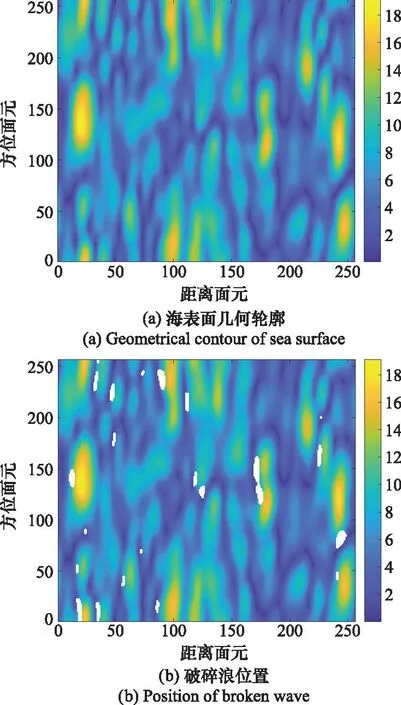
图2 高海情下的海表面及破碎浪位置Fig.2 Sea surface and broken wave’s position with high sea conditions
(1)

1.2 舰船回波建模
三维摆动舰船成像几何模型如图3所示,舰船坐标系假定为OXYZ,其中坐标系的原点O为舰船参考成像中心,舰船三维旋转角速度可表示为矢量ω;雷达视线在OXYZ中的归一化矢量为n; 角速率矢量ω在雷达视线方向的投影为ωR,在垂直雷达视线方向的投影为ωe,ωR和n平行,不会产生多谱勒频移;ωe和雷达视线垂直,该旋转分量将会导致多谱勒频移,是方位聚焦和散焦的主要原因。假设目标上第p个散射点到坐标原点O的矢量为rp,则可以通过计算得到该点的线速度为ωe×rp,对应的径向分量为(ωe×rp)·n。

图3 三维摆动舰船成像几何模型Fig.3 Geometric model of three-dimensional swinging ship imaging
假设雷达发射LFM信号并采用去斜处理的方法,发射信号为
(2)

目标距离-慢时间回波为
(3)
式中:B=γTp为发射信号带宽;r为距离取值(距离分辨率c/2B的整数倍);σp为散射点p的强度。在tm时刻,Rrpy(tm)=rp·n为散射点p与参考成像中心的距离(即rp)在径向n的投影。
根据图3可知,随着时间推移,Rrpy(tm)为散射点p线速度径向分量(ωe×rp)·n的积分,即

(4)
假设散射点p的坐标为(xp,yp,zp),ωe在坐标轴上的分量分别为ωex,ωey,ωez,对于复杂运动目标,它们都是时变的,可以进行二阶近似:
(5)
式中:ωx,ωy,ωz,λx,λy,λz,γx,γy,γz分别表示为角速度的常数分量系数、线性分量系数以及二次分量系数。将式(5)代入式(4)可得:
(6)
式中:‘·’表示两矢量内积;ω=[ωx,ωy,ωz];λ=[λx,λy,λz];γ=[γx,γy,γz];r=[(ypzR-zpyR),(zpxR-xpzR),(xpyR-ypxR)];Rrpy(t0)为初始时刻t0,散射点p与成像中心O的距离(即rp)在径向n的投影。
根据式(6)可知,Rrpy(tm)将造成越距离单元走动,其线性距离走动借助Keystone变换校正。若目标的某个距离单元中包含P个散射中心,可得到对应的方位向回波为
(7)

(8)

2 高海情下舰船成像
高海情下的舰船三维摆动,使得雷达观测到的角速度矢量随时间不断变化,其中模值变化将导致海面舰船目标的转动速度时变,而指向的变化将导致ISAR成像平面的改变。时间段选取的思想是从三维摆动过程中寻找转速和成像平面稳定的时间窗,在该时间窗内采用RD方法进行成像。考虑到时间窗由海浪涌动下舰船的摇摆特点决定,难以保证多普勒分辨率的要求。
本文通过对高阶信号的MDCFT处理[11]提高雷达回波的相参积累时间。成像算法流程如图4所示,成像具体步骤如下:
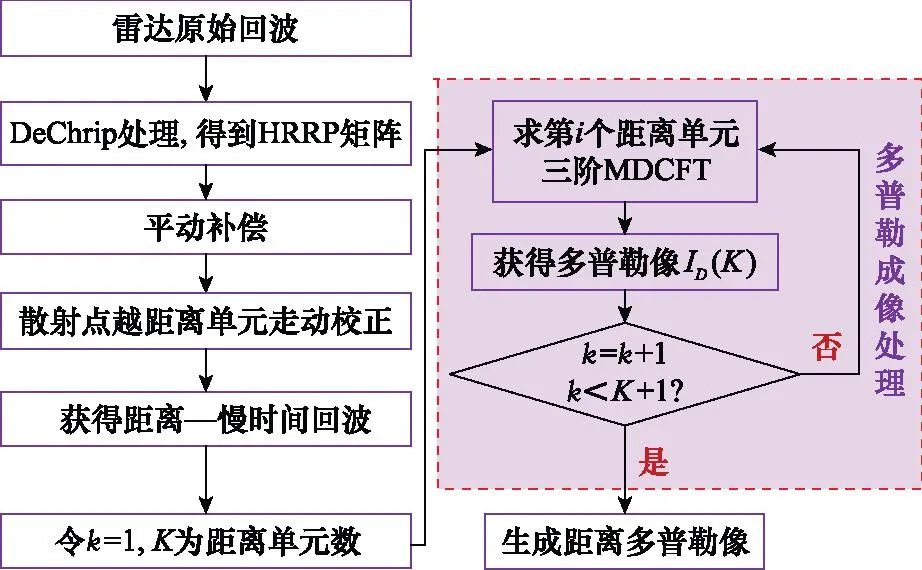
图4 三维摆动舰船成像流程图Fig.4 Imaging flowchart of three-dimensional swinging ship
步骤 1根据式(8),s(nr) 的离散chirp傅里叶变换(discrete chirp Fourier transform, DCFT)为
(9)
步骤 2在三维DCFT域(k,l,m) 中,Sc(k,l,m)沿l轴和m轴的积分后的结果反映了在k轴的多普勒聚焦效果。因此,通过沿l轴和m轴的积分可获得该距离单元对应的多普勒成像结果ID(k)。ID(k)可表示为
(10)
步骤 3综合所有距离单元,可获得目标RD。
假定目标散射中心分布如图5(a)和图5(b)所示,舰船航行径向速度及加速度分别为vr=10 m/s和ar=10 m/s2。在初始时刻t0,雷达和舰船目标的初始距离为R0=40 km。雷达及舰船三维旋转参数如表1和表2所示。ISAR成像相干累积时间为TCPI=0.7 s,则信号采样点数为Nr=TCPI·PRF=700。图5(c)和图5(d)分别给出了RD方法和MDCFT方法的成像结果,由图可见,舰船目标的多普勒维存在散焦现象,且舰首和舰尾的散焦尤为明显,这是因为RD成像的适用条件是成像时间内目标上各散射中心多普勒恒定,而三维摆动舰船的多普勒频率具有随机和不稳定性(舰首和舰尾最为明显),使得信号无法实现相参积累。而MDCFT方法将多普勒回波建模为三阶相位信号,对多普勒频率的变化感知更加准确。从图5(d)可见,舰船在多普勒维具有良好的聚焦效果,成像结果表明,MDCFT方法更适用于三维摆动目标的雷达成像。

表1 雷达参数Table 1 Radar parameters
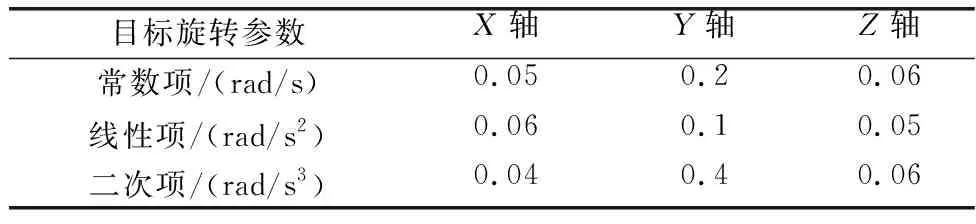
表2 舰船三维旋转参数Table 2 Three-dimensional rotation parameters of ships


图5 三维摆动舰船成像仿真结果Fig.5 Imaging simulation results of three-dimensional swinging ship
3 基于ISAR图像的弹载雷达导引头海面目标检测方法
高海情下,采用上述方法对海面舰船的典型成像结果如图6所示。由图6可见,由于海尖峰的大量存在,采用传统恒虚警率(constant false alarm rate, CFAR)检测必然会出现虚检。高海情下舰船目标检测的关键在于海杂波特性的深度认知、精细感知和充分利用[15]。通常采用杂波和目标回波的差异性特征实现检测,特征是用以描述杂波与目标之间差异性的指标,根据海尖峰与舰船回波在RD图像中的尺度特征差异,本文提出一种基于水平集方法的舰船目标检测思路。
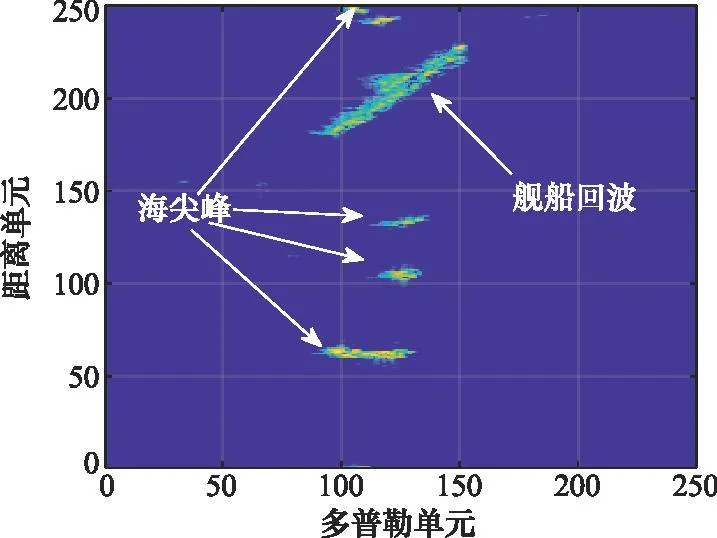
图6 高海情环境下舰船典型成像结果Fig.6 Typical imaging results of ships in high sea conditions
3.1 基于水平集的舰船与海面区域划分
水平集方法是计算机视觉中的用于形状建模的数值计算方法。其优点是可以对演化中的目标轮廓进行数值计算,而不必对轮廓参数化。另一个优点是可以便捷地追踪目标轮廓的改变。例如,当目标的轮廓一分为二、产生空洞等。这些特点使得水平集方法成为随时间变化的物体建模的有力工具。图7给出了不同时刻的水平集的轮廓演化示意图。

图7 水平集的轮廓演化示意图Fig.7 Outline evolution schematic diagram of level set
基于水平集的区域划分包含如下步骤:

步骤 2曲面轮廓的迭代方程可表示为
(11)
式中:F为梯度函数,表示迭代速度的大小,对于t=nΔt,离散化的迭代方程可表示为
(12)
步骤 3假定φ0曲面与实际雷达图像的大小一致,建立一个C(0)对应的闭合轮廓S0,使其满足如下表达式
(13)

(14)
式中:ε为较小的常数;kij为(i,j)处的斜率;M1和M2为本文算法分别分割的在对应区域的平均值;fij为坐标(i,j)处的像素值。

本文利用仿真数据进行验证,实验结果表明,经过500次左右的迭代,水平集的划分结果将趋于稳定,此时对应的划分结果可作为目标区域二值分割的结果。
3.2 高海情下舰船目标检测策略
水平集算法具有无需人工干预、自主迭代、无需大量数值计算等优点,适用于弹载雷达对海探测的应用背景。本文将水平集算法应用于高海情下的舰船目标检测,其基本策略流程如图8所示。

图8 基于水平集的舰船目标检测流程Fig.8 Ship target detection process based on level set
检测流程包含4个步骤。首先对雷达基带回波采用MDCFT算法进行成像处理,获得包含目标与海杂波的距离多普勒图像,由于海尖峰位置相对固定,与舰船运动规律存在差异,MDCFT算法对杂波信号具有一定的抑制能力;然后,采用水平集方法对RD图像进行二值分割,由于水平集方法得到的结果是多个区域的闭环曲线,因此,输出结果具有初步的聚类属性;在此基础上,采用经典的DBscan算法即可实现对输出区域的有效聚类;最后,分别对不同目标区域进行特征提取,并根据提取得到的特征判断目标真实身份,从而实现高海情下舰船的有效检测。
在高海情下,破碎浪的位置通常是海表面斜率最大的位置,该位置的浪通常以大致相等的速度运动,而对于大型舰船而言,不同位置受到的浪涌的推力存在差异,造成舰船首尾先对雷达的速度存在一定差异,因此多普勒展宽更加明显。同时,距离分辨率由带宽决定,径向距离是雷达图像中最可靠的特征。本文将径向尺寸和多普勒展宽作为判断检测区域是否为目标的依据,判决表达式如下:
(15)
式中:L为目标径向长度;LD和LU分别为舰船目标的长度上限与下限;LU取值通常为舰船目标可能的实际最大长度,本文中LU取值为LD=LU/5;BDoppler为方位向多普勒展宽程度;BD为展宽门限,在实际应用中通过海情等级和雷达信号积累时间估算得到。
4 实验验证
假定高海情下的海表面轮廓与破碎浪位置如图2所示,目标散射中心分布如图5(a)和图5(b)所示,舰船航行径向速度及加速度分别为vr=10 m/s和ar=10 m/s2,仿真初始时刻为t0,舰船目标到雷达的距离为R0=40 km。雷达工作参数与舰船三维转动参数总结如表1所示。图9分别给出了海表面和舰船的一维距离像,将距离像矩阵相加获得舰船与海表面复合的距离像回波。

图9 海杂波与舰船一维距离像矩阵Fig.9 HRRP matrix of ships and sea clutter
采用MDCFT算法对其进行二维成像,得到的成像结果如图10(a)所示,图10(b)和图10(c)分别给出了二维恒虚警率(constant false alarm rate, CFAR)检测方法和水平集方法的检测结果,其中二维CFAR检测需要对目标窗口、保护窗口、背景窗口3的大小进行设置,本仿真中分别设置为1,20和50。可见,当参数设置合理时,采用水平集方法和CFAR方法均能有效提取目标区域。若将3个窗口对应的参数分别设置为1,5和10时,对应的CFAR检测结果如图10(d)所示,存在连片状目标中间强散射点无法检测的情况,而本文方法不需要对检测窗进行设置,避免了由于参数设置不合理带来的影响。需要指出的是,采用仿真软件进行计算,所提方法步骤1的迭代收敛的计算时间为554.07 ms,这相对弹载实际应用而言,还存在一定的差距,后续需要针对弹载平台硬件条件及应用环境对算法进行优化设计,以满足实际应用需求。


图10 高海情舰船成像及初步检测结果Fig.10 Imaging and preliminary detection results of ships with high sea conditions
采用DBScan聚类算法对水平集算法输出区域的聚类结果如图11所示,由于水平集的输出结果是闭合的,因此在进行聚类时只需要将闭合区域进行聚类即可,由结果可知,聚类算法能够实现对RD图像中各个目标的有效聚类。将径向距离和多普勒展宽作为区分舰船与海杂波的特征,分别对每个目标进行提取,得到的特征值如表3所示。可见舰船(目标1)的径向长度与多普勒展宽等特征与海尖峰存在明显的差异,为高海情下海面舰船的检测提供了一种可行的思路。

表3 目标特征估计结果比较Table 3 Comparison of target feature estimation results

图11 DBScan聚类结果Fig.11 Cluster results of DBScan
5 结 论
高海情下弹载雷达探测面临两方面的挑战,一是舰船三维摆动造成RD图像散焦;二是海尖峰的存在增加了虚检概率。本文将MDCFT与水平集算法组合,提出一种新的成像检测思路。首先通过MDCFT算法对三维摆动的舰船回波进行多普勒聚焦,消除回波相位高阶项带来的RD图像散焦;其次,利用水平集算法初步检测图像中的目标区域,然后利用聚类算法获取每个目标的区域;最后提取目标特征并用于判决目标是否为舰船,检测过程不需要设置目标窗、保护窗、背景窗等参数,避免了参数设置导致的性能下降;最后利用仿真实验验证了算法的有效性。该方法综合考虑了目标成像与检测性能的提升,具有较好的检测性能。需要指出的是,由于缺乏实测数据,本文根据相关参考文献[1]仿真了海杂波并用于算法验证,后续将利用实测数据进一步验证并优化所提算法的性能。

