考虑乘客旅行时间价值的市域轨道交通列车开行方案

罗 晋 朱海燕 刘志钢 戴卫杰

(1. 上海工程技术大学城市轨道交通学院, 201620, 上海; 2. 上海申通地铁集团市域铁路运营筹备组, 200122, 上海)

列车开行方案反映了铁路乘客经营策略和服务质量水平[1]。针对列车开行方案的理论与方法,学者们进行了深入的分析与研究。文献[2]构建了以运输部门效益最大、乘客时间最小化为目标的列车开行方案优化模型;文献[3]建立了运力浪费和乘客等待时间最小化的优化模型;文献[4]基于铁路收益和乘客出行构建了多目标模型;文献[5]以乘客旅行时间和城市轨道交通总成本最小为目标,构建了双目标规划模型。

列车开行成本与乘客出行成本是影响列车开行方案编制的主要因素。现有研究在分析乘客出行成本时,往往只考虑旅行时间而忽视时间价值。时间价值是时间的货币表现[6],时间价值差异体现在出行目的、收入等乘客属性上,不同乘客的时间价值不同,因此单位时间内的出行成本也不相同。市域铁路客流具有通勤化、潮汐性等特点,包含了通勤通学、商务公务、旅游休闲,以及日常购物、就医等不同种类的客流,既具有干线铁路速度快、越行运输的组织特点,又具有城市轨道交通运量大、开行密度大、公交化的特点。考虑乘客旅行时间价值的列车开行方案对满足市域铁路不同乘客的旅行时间需求,凸显市域铁路的功能及定位,增强与其他运输方式的竞争实力,以及提高社会经济效益具有重要意义。

1 考虑乘客旅行时间价值的列车开行方案模型构建

1.1 目标函数

1.1.1 出行成本

乘客出行成本由旅行时间和时间价值构成。旅行时间包括列车运行时间、停站时间及候车时间,其中:列车运行时间由路程以及设备设施条件来决定,而停站与候车时间与开行方案关系密切。由于运输设备、旅行距离等原因导致列车运行时间基本不变,因此乘客由于列车运行时间产生的出行成本不变。而停站和候车时间可以通过优化运营组织进行改变,因此应使这部分时间产生的出行成本目标函数Zp最小。如式(1)所示:

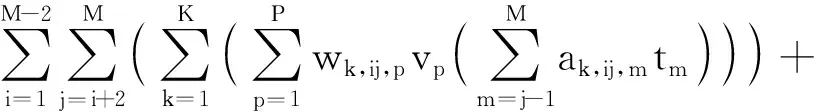
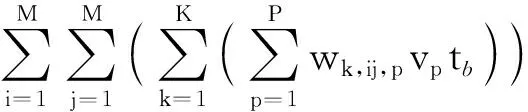
(1)

式中:

wk,ij,p——车站i(起点)至车站j(讫点)且类型为p的乘客,选择停站方案为k的乘客人数;

ak,ij,m——0-1变量,当车站m是停站方案k在径路车站i至j的中间站停站时,其值为1,否则为0;

tm——列车在车站m的停留时间,包括停站与起停附加时间;

vp——类型为p的乘客的单位旅行时间价值;

tb——乘客平均候车时间。

1.1.2 开行成本

列车开行成本是指开行1列列车所必须支出的能耗、设备折旧,以及其他费用。不同编组列车的车辆数不同,而在固定线路上每辆车的单位运行成本基本不变,因此不同编组列车的开行成本不同。本文的列车开行成本由列车开行数量与列车编组构成,因此开行成本最小化的目标函数Zs为:

(2)

式中:

Ca——列车开行编组方案a的运行成本;

qka——0-1变量,当停站方案k采用方案a时,其值为1,否则为0;

xk——停站方案为k的列车开行数量。

1.2 约束条件

1.2.1 列车定员约束

列车在停靠时存在乘降客流,在车的乘客数量会发生变化,但列车在站间运行时乘客数量保持不变,任一区间的在车人数都不能超过列车定员。延伸到任一停站方案,在有多个车辆编组选择的情况下,列车定员都可以表示为1个约束集合,即列车定员约束集合Sk:

(3)

式中:

wk,lm——车站l至车站m且停站方案为k的乘客人数;

wk,ij——车站i(起点)至车站j(讫点)且停站方案为k的乘客人数;

η——列车上客率;

据说人类迟早要被人工智能控制，而电子产品是人工智能派来的先遣小分队。在我看来，如果非得拧巴着不做“低头族”，和这支小分队誓死对抗，不但反人性，还反智性，显然是没有胜算的，不如缴枪算了。

Qa——编组方案a的列车定员。

1.2.2 站间客流约束

列车流不仅要满足总的客流需求,也要保证站间的客流需求,即线路上所有列车从车站i到车站j所带走的客流不能低于需求量ROD,ij。所有站间客流约束集合ROD为:

(4)

式中:

ROD,ij——车站i至车站j的客流需求。

1.2.3 列车开行数量约束

停站方案是指开行各列车的停站序列。线路上列车的开行数量由各停站方案开行的列车数决定,即:

(5)

式中:

N——列车开行数量。

线路上的最大断面客流量决定了列车的最低列车开行数量。为了满足客流需求,列车开行数量最少应满足站间最大断面客流,即:

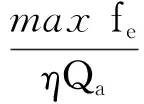
(6)

式中:

fe——区间断面e的客流量。

但列车最大开行数量不应超过线路的通过能力,即:

(7)

式中:

di——开行停站方案i的列车通过能力扣除系数;

to——线路运营时间;

tg——最小发车间隔。

1.3 帕累托模型求解

本文所构建的是一个多目标规划模型,帕累托曲线是解决多目标问题的较好选择。该曲线完全基于原始数据,未将问题转化成单目标问题分析,亦不需要设定或引入新的参数,不会丢失目标函数和解的信息,解的优劣可以较好保证。帕累托模型提供了客观的最优决策点,但需结合决策者的主观偏好,确定最终的最优决策点。该模型求解的关键是确定不同乘客的时间价值,以及不同编组列车的开行成本,即主要是对式(1)和式(2)中的vp及Ca进行标定。目前研究中确定时间价值及开行成本的方法较多,采用不同方法得到的结果不同,为避免误差,本文采用比值的形式对上述两参数进行标定。

2 实例分析

上海轨道交通市域线机场联络线(以下简称“机场线”)是上海市在建的市域轨道交通线路之一,线路呈“Y”字型结构。机场线线路见图1。机场线单向远期高峰小时预测客流量见表1。考虑了4节编组及8节编组两种列车编组方案;组织了两个交路:① 上海南站站→三林南站→上海东站站;② 虹桥站→三林南站→上海东站。本文主要研究机场线虹桥站→上海东站站方向高峰小时的列车开行方案。

图1 机场线线路图

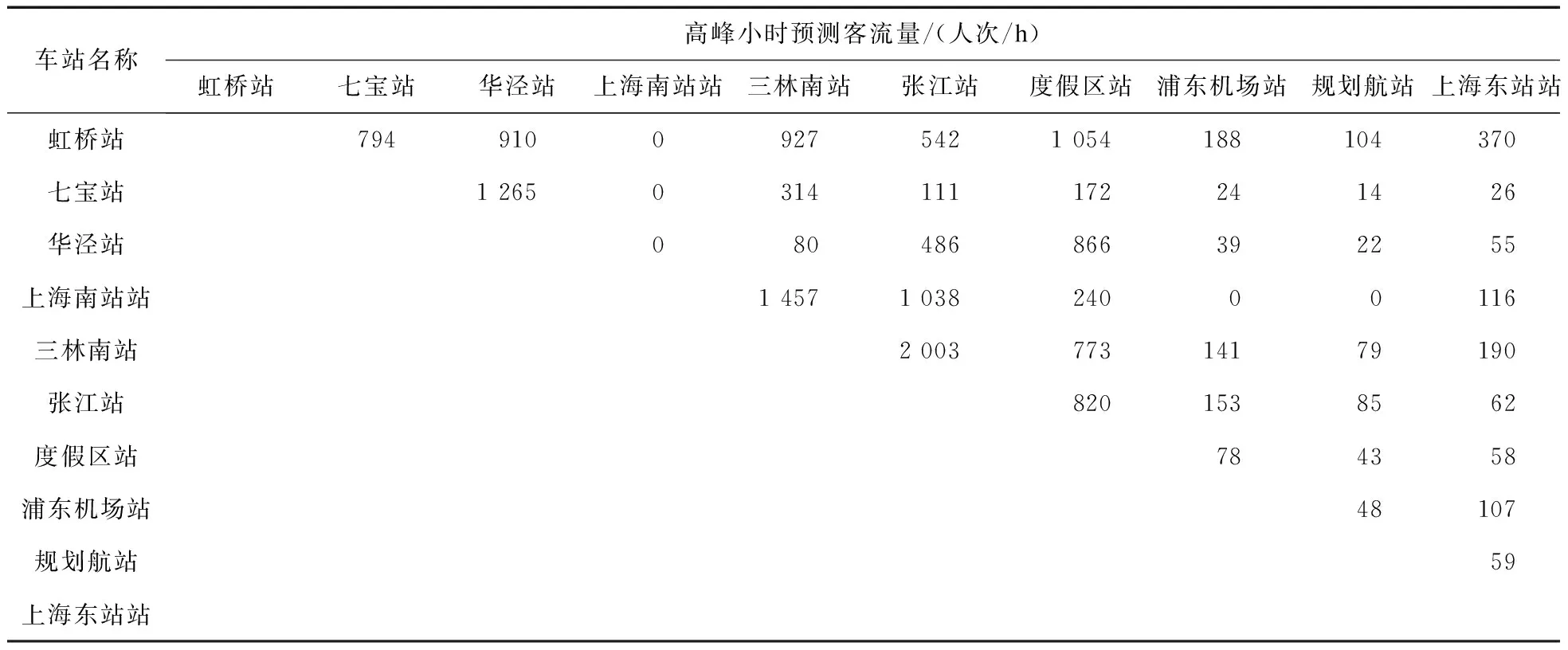
表1 机场线单向远期高峰小时预测客流量

基于线路功能特征对乘客进行分类,机场线中目的地为火车站及机场的客流要求停站少、旅行速度快,时间价值较高,节省下来的时间可以创造更多的社会价值;而机场线沿线其他车站间的客流以通勤为主,对旅行速度的要求相对较低,时间价值较低。将乘客划分为两类:P1为其他目的地的乘客;P2为目的地为机场及车站的乘客。机场线的基本参数取值见表2。

表2 机场线的基本参数取值

本文考虑4节编组及8节编组两种列车编组方案,由此定义两种编组下的列车开行成本比C1/C2=1.00∶1.75。乘客旅行时间价值可分为v2/v1=1及v2/v1≠1两种情况:当v2/v1=1时,代表两类乘客的时间价值无差别,即未考虑时间价值的情况;当v2/v1≠1时,v2/v1为不同取值下的结果不同。

2.1 不同乘客旅行时间价值下的模型结果

通过计算得到考虑乘客旅行时间价值前后v2/v1不同取值下的帕累托解(见图2)。解集中的每个个体都对应1种列车开行方案。乘客旅行时间价值与不同编组列车的开行成本采用比值确定。

由图2可以看出:考虑乘客旅行时间价值后,制定的列车开行方案的出行成本均不低于考虑乘客旅行时间价值前制定的列车开行方案的出行成本;随着v2/v1取值增大,考虑乘客旅行时间价值后制定的列车开行方案的出行成本与考虑乘客旅行时间价值前的差距也逐渐增大。由此可以得出,考虑乘客旅行时间价值制定的列车开行方案能最大限度地减少乘客出行成本。

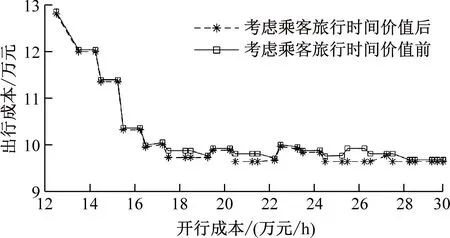
a) v2/v1=1.25

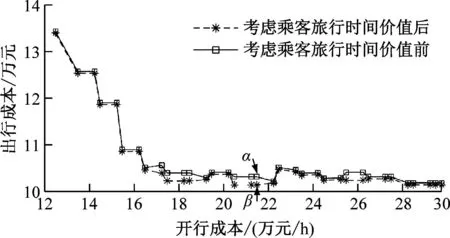
b) v2/v1=1.50

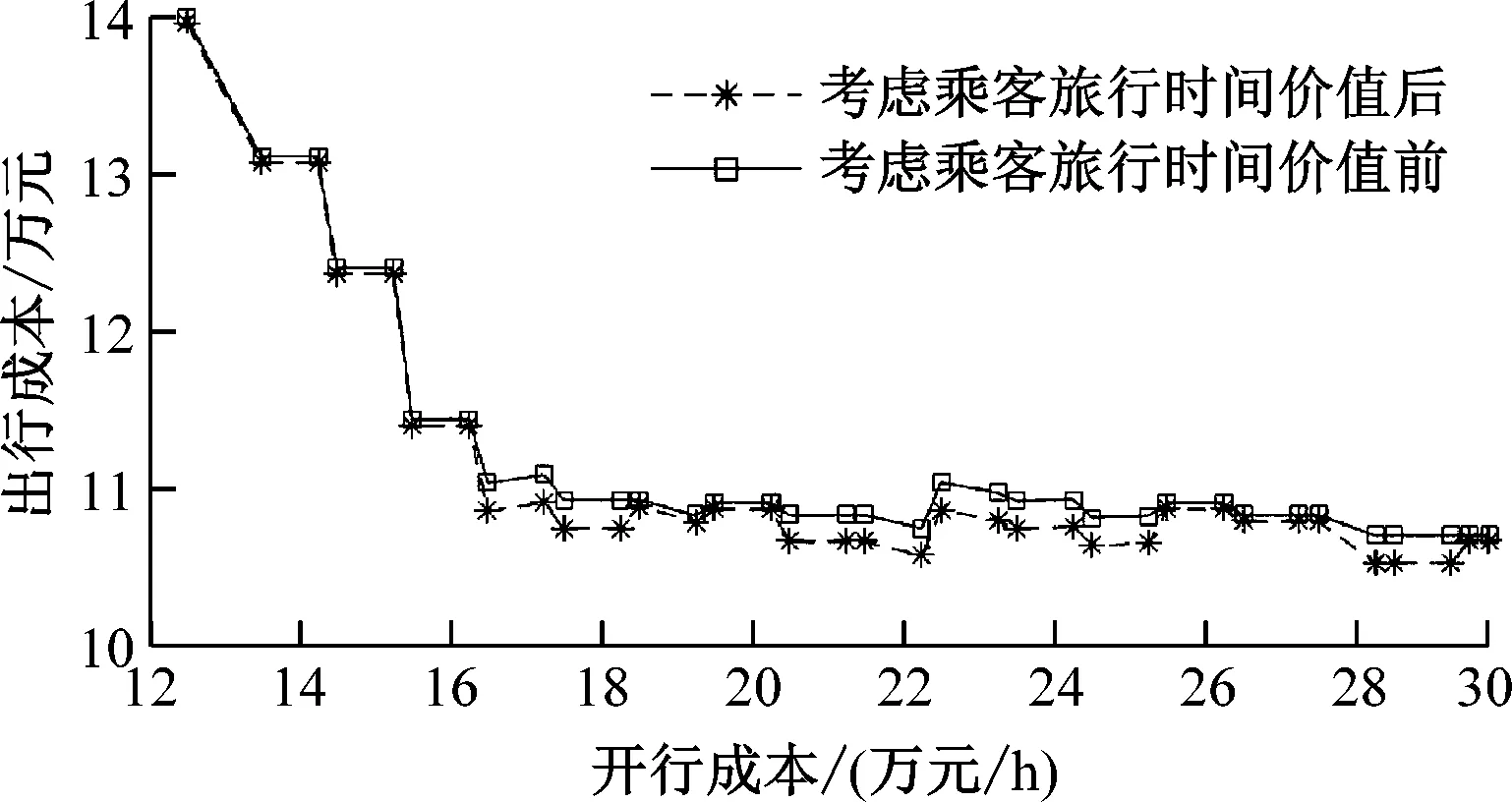
c) v2/v1=1.75

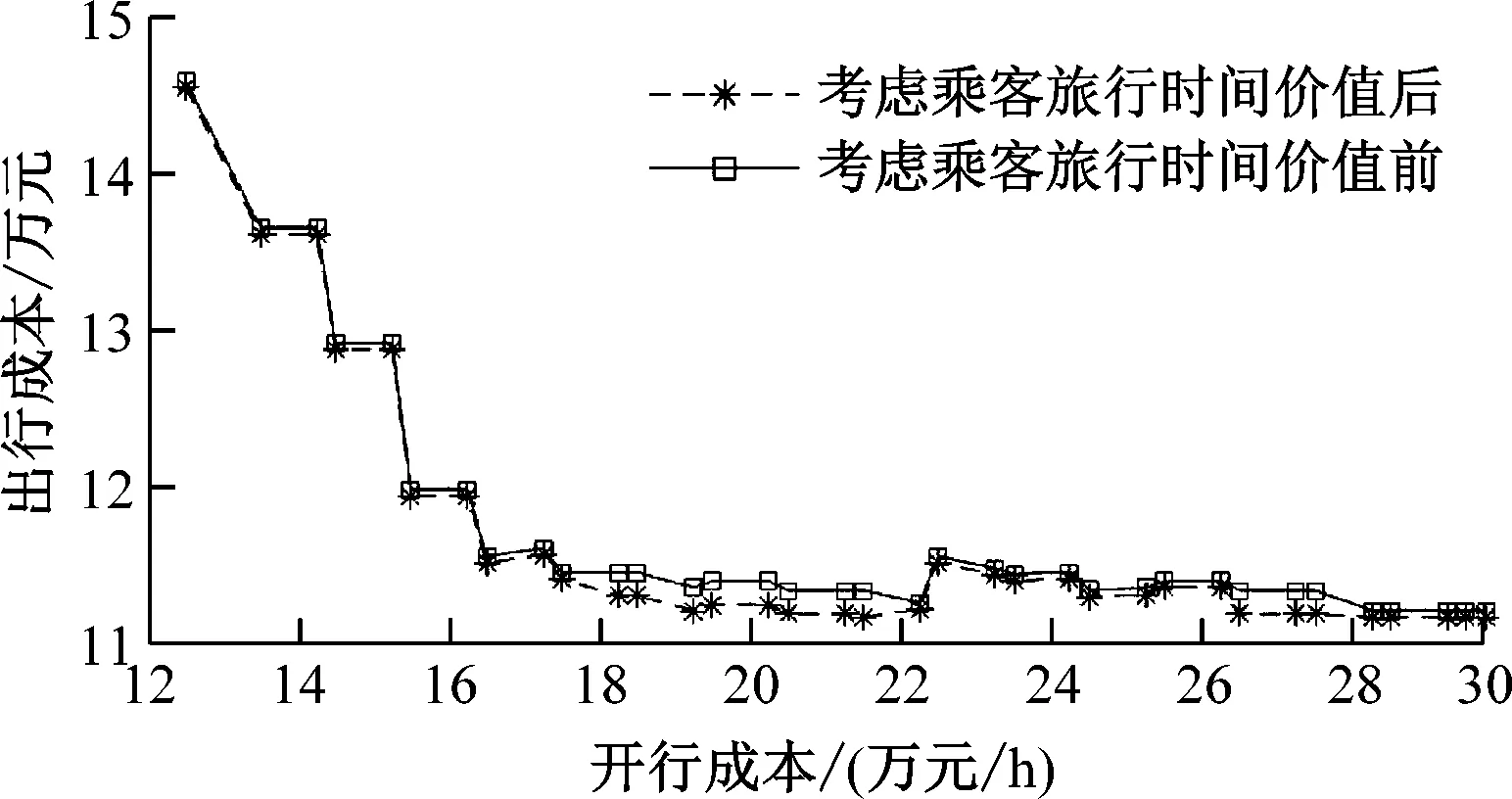
d) v2/v1=2.00

2.2 列车开行方案对比

选取开行成本与时间价值一定的情况下,考虑时间价值前后的开行方案进行分析。选取图2 b)中的α、β两点所代表的开行方案A、B进行对比分析,乘客旅行时间价值比v1/v2=1.5,开行成本为21.5万元/h,越行站设定在张江站及浦东机场站。机场线的停站方案见图3。机场线列车编组方案见表3。机场线列车开行方案评价指标见表4。

a) 停站方案1

b) 停站方案2

c) 停站方案3

d) 停站方案4

表3 机场线列车编组方案

表4 机场线列车开行方案评价指标

由表4可见:相较于方案A,方案B在开行成本一定的情况下,减少了列车总停站次数,降低了乘客的停站等待时间;方案B减少了乘客的停站候车出行成本和总停站候车时间,乘客P1的平均停站候车时间增加了0.36 min,乘客P2的平均停站候车时间减少了0.15 min。由于乘客P2的乘客旅行时间价值要高于乘客P1,虽然小幅度增加了P1的旅行时间,从而增加了这类型乘客的出行成本,但从经济角度上看,增加的成本能通过减少乘客P2的出行成本进行弥补,同时获得更大的经济效益。

3 结语

本文构建了考虑乘客旅行时间价值的列车开行方案模型,并以机场线为研究对象,对该模型进行了分析。结果表明,考虑乘客旅行时间价值后制定的列车开行方案能最大限度地减少乘客出行成本;从宏观经济的角度上看,增加乘客旅行时间价值较低的乘客旅行时间,缩短乘客旅行时间价值较高的乘客旅行时间,能更好地发挥列车开行方案的经济效益。