干式电抗器的建模与故障预警方法研究

刘 轩，郑 璐，荀 华，付晓艺，曹 懿

（1.内蒙古电力（集团）有限责任公司内蒙古电力科学研究院分公司，呼和浩特 010020；2.内蒙古电力（集团）有限责任公司乌兰察布供电分公司，内蒙古 乌兰察布 012300；3.内蒙古电力（集团）有限责任公司包头供电分公司，内蒙古 包头 014000）

0 引言

干式电抗器作为远距离交流输电系统的主要辅助设备，在系统中发挥补偿容性电流、维持系统电压水平、提高线路传输能力等作用，一定程度上促进了电网的发展[1-5]。但是在长期运行中，部分干式电抗器会发生匝间短路等故障，严重时会导致火灾，对电网的安全性造成极大威胁[6-11]。干式电抗器的热点温度与其寿命直接相关，准确计算干式电抗器的温度场分布有助于故障预警，现场运维人员收到预警信息后及时采取措施能够降低故障发生概率，提高电网运行的安全性与稳定性[12-16]。

目前，国内外学者主要采用流体-温度场耦合法对干式电抗器的温度场进行研究[17]。该方法利用有限元计算，通过赋予电抗器表面不同的对流换热系数，给出电抗器绕组径向上的温度变化，但该方法仍然依靠经验公式来确定对流换热系数。文献[18]采用有限容积法对三维模型的稳态流体场与温度场进行直接求解，获得温度场分布特性，研究包封轴向及径向的温度分布规律。文献[19]采用流体-热力学耦合的仿真计算方法，结合温升实验，对干式平波电抗器的温度场分布特性进行了研究。文献[20]以干式铁心电抗器为研究对象，通过多物理场耦合仿真探究了电抗器的温升及振动机理，并搭建了干式铁心电抗器系统级协同优化模型，提出了提高金属导体利用率的协同优化设计方法。文献[21]按照电抗器实物尺寸利用仿真软件建立了三维流场-温度场模型，并采用迭代计算方法得出干式空心并联电抗器的温度场。以上文献中的模型未与磁路模型进行融合，未进行简化和降阶，计算复杂程度高。基于此，本文对相关模型进行融合与简化，提出一种基于多物理场耦合模型的干式电抗器故障预警系统，旨在提升故障诊断与预警的精准性、快捷性。

1 干式电抗器多物理场融合模型构建

本文以35 kV、2000 kvar 干式电抗器为研究对象，提出建模与故障预警方法，其总体原理如图1所示。

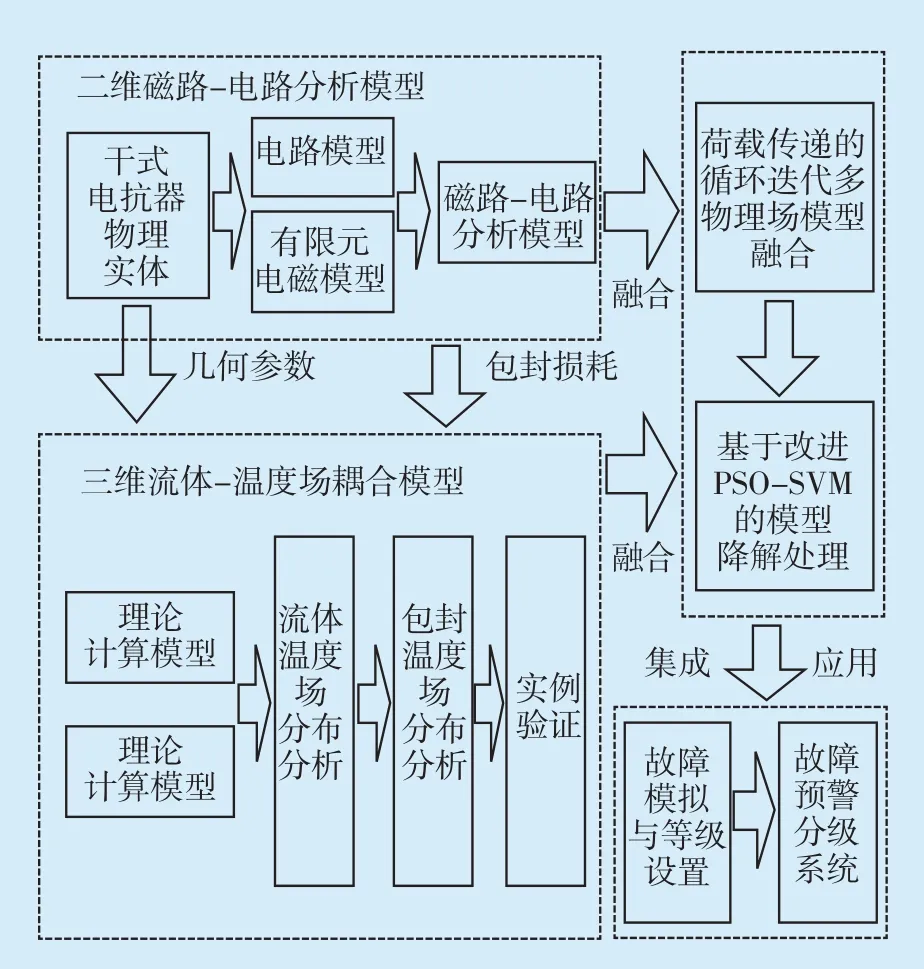
图1 干式电抗器建模算法示意图Fig.1 Schematic diagram of dry reactor modeling algorithm

电抗器上下两端各有一星型支架作为进出线汇流，同时给包封提供机械夹紧力。在电抗器包封之间沿径向布置若干细小的聚酯撑条，撑条之间的气道构成包封间的散热通道。包封中的绕组由多层线圈并联构成，每层线圈由多股圆形铝导线并联绕制而成，每层线圈表面绕有聚酯薄膜和浸渍环氧胶的无纺布，包封表面的绝缘材料为玻璃纤维增强环氧树脂。干式电抗器的主要参数如表1所示。

表1 干式电抗器的主要参数Tab.1 Main parameters of dry reactor

1.1 电磁-电路二维模型构建

按照干式电抗器的型号和实际尺寸，建立包括空气、绝缘介质以及线圈的二维分析模型，该模型包括有限元磁场模型和电路模型两部分。采用三角形网格对干式电抗器进行剖分，该剖分方法对于二维模型的描述较为细微平滑。干式电抗器由n层同轴螺线管并联而成，绕组层数为m，每层线圈均可等效为一条支路，支路中包含该层线圈的电感Wi与线圈直流电阻R（ii=1，2，…，n），每两条支路之间存在互感Mmn，如图2（a）所示。当发生匝间短路故障时，干式电抗器会形成一个短路环，如图2（b）所示，其中短路环的直流电阻为Rn+1；电感为Wn+1。根据法拉第电磁感应定律，短路环中会产生感应电流。短路环与其余各层线圈之间产生互感M（in+1），剩余各层线圈中的互感也发生改变。

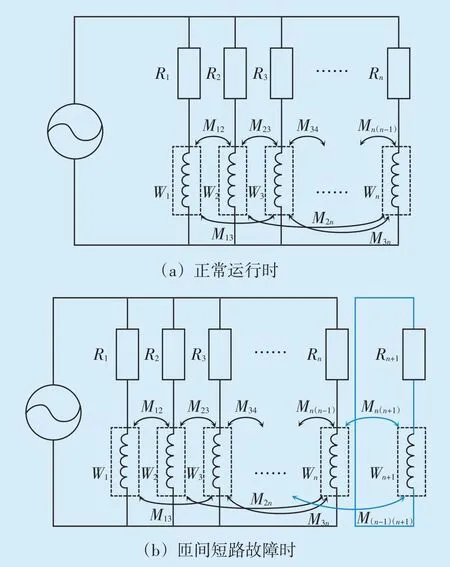
图2 电磁-电路分析模型Fig.2 Electromagnetic-circuit analysis model of dry reactor

根据以上搭建的模型对干式电抗器运行过程中的磁场进行仿真计算，得到电抗器的磁场分布，如图3所示。

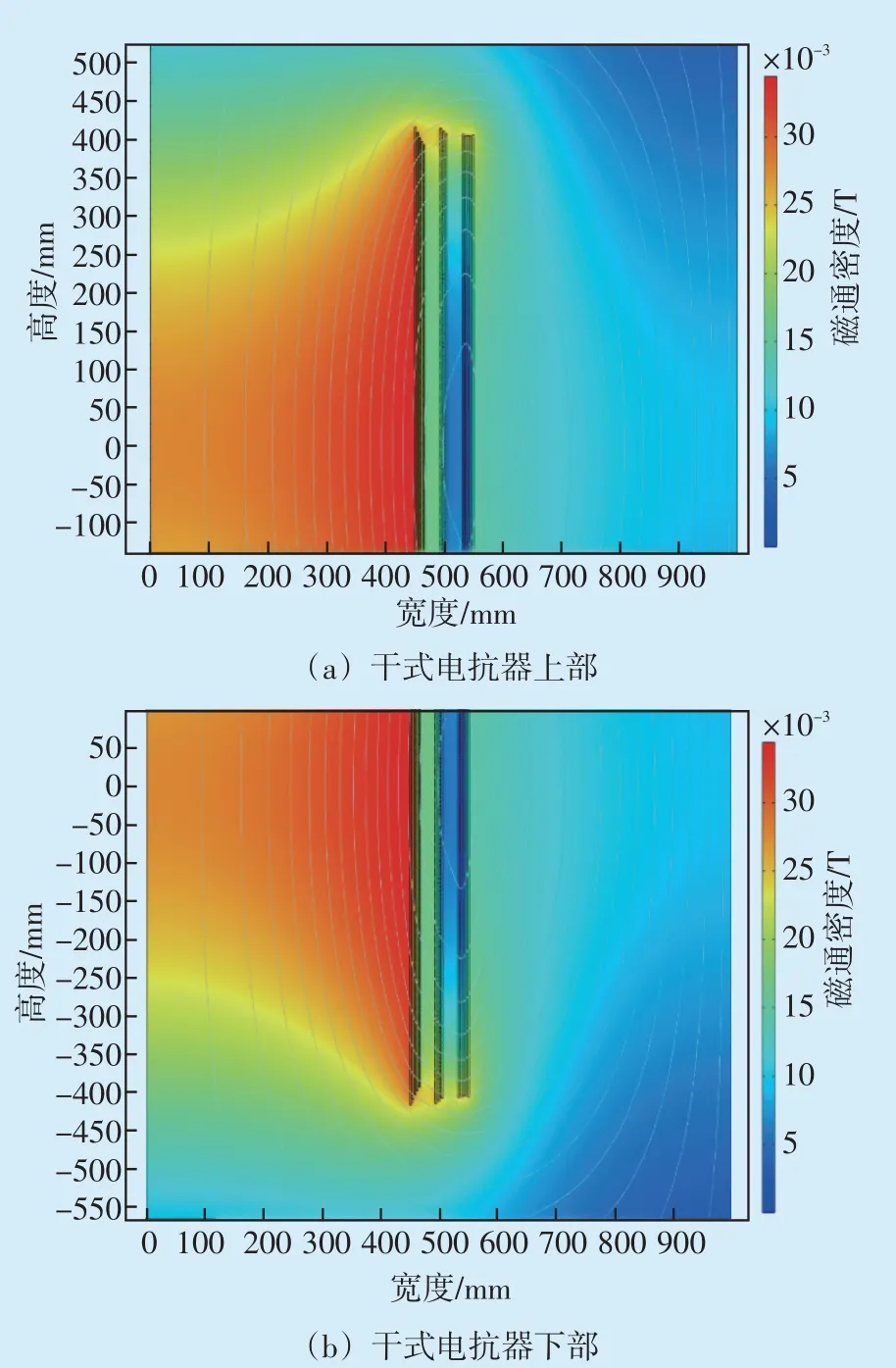
图3 干式电抗器磁场分布图Fig.3 Magnetic field distribution of dry reactor

1.2 三维流体-温度场有限元模型构建

本文在建立三维流体-温度场耦合计算模型时，利用式（1）计算得到包封损耗，并将其作为三维流体-温度场的热源来计算电抗器的温度场和流场分布[22]。

式中：Pj为第j 匝绕组损耗，主要包括电阻性损耗Paj和涡流损耗Pbj。

Paj和Pbj的计算公式如下：

式中：Dj为第j 匝导线的线径；γ为铝导线的电导率；ωangel为施加激励的角频率；Ij为第j匝导线的半径；Bj为第j匝导线中心处的磁感应强度。

1.2.1 模型假设

（1）模型具有轴对称性，包封、防雨罩、星形支架对称面可视为绝热面。

（2）包封间温差较小，辐射传热占比小。电抗器内部的热交换以对流和传导为主，防雨罩外表面与外冷却空气的热交换以对流和辐射为主。防雨罩表面比辐射率的取值为0.9。

（3）包封视为同性材料整体，防雨罩与星形支架视为线性材料，不考虑材料参数与温度之间的非线性关系。

（4）计算模型的空气域为电抗器防雨罩、最外层包封、下星形支架之间的空气。

1.2.2 模型边界条件

（1）在计算域边界Γ1、电抗器固体和空气交界面Γ3上指定无滑移边界条件，即vx=vy=vz=0，表面比辐射率取0.9（Γ1、Γ3分别为第1类、第3类边界条件，vx、vy、vz分别为x轴、y轴、z轴方向上的空气流速）。

（2）在计算域边界Γ1上指定恒温边界条件，即T|Γ1=T0，设定电抗器周围环境温度为293.15 K。

（3）设置重力加速度为9.81 m/s2，方向为z轴的负方向。

（4）绕组包封内的热源大小由电磁场计算得到的绕组损耗决定。

划分网格、施加边界条件后，本文在干式电抗器第一层绕组高度7/8 的位置设置匝间短路故障，短路匝数为2 匝。电抗器在环境温度为25 ℃的条件下运行30 min后，进行温度场仿真，结果如图4所示。从图中可知，电抗器包封的温度高值集中在短路位置附近，温度最高值为219.0 ℃，故障包封的温度变化趋势为由故障绕组向非故障绕组逐渐降低。

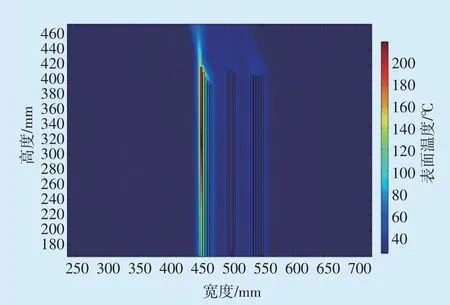
图4 干式电抗器匝间短路时的温度场分布图Fig.4 Temperature field distribution of dry reactor during inter-turn short circuit

2 多物理场模型融合与降阶

2.1 多物理场模型融合

采用载荷传递的循环迭代算法对多物理场模型进行融合。由于导体电阻率与温度有关，因此需要在电磁场中计算初始温度下电抗器每个包封中的电流和损耗，并施加边界条件进行磁场分析，同时对各绕组的电流和损耗进行仿真计算。将包封损耗作为三维流体-温度场有限元模型的热源，施加载荷、流场和温度场边界条件，进行温度场和流场分布计算。若相邻两次温度差小于设定值或者达到循环次数，则达到收敛条件、停止迭代，完成多物理场模型融合。本文中，迭代次数设置为100次，相邻两次温度差设定为5%。

2.2 三维流体-温度场有限元模型降阶

上述方法在流体-温度场模型计算上虽然精确、直观，但流程构建复杂、计算速度慢。为了在保证计算精度的同时简化模型构建流程、提高计算速度，引入PSO-SVM的代理模型算法对三维流体-温度场有限元模型进行降阶。但是，PSO 算法容易陷入局部最优解，出现局部收敛问题。为此，本文提出一种改进算法，即采用信息熵结合差分变异中的变异策略来解决该问题，可以有效弥补PSO算法在后期迭代中种群多样性迅速降低的缺陷。改进PSO优化SVM的过程如图5所示。

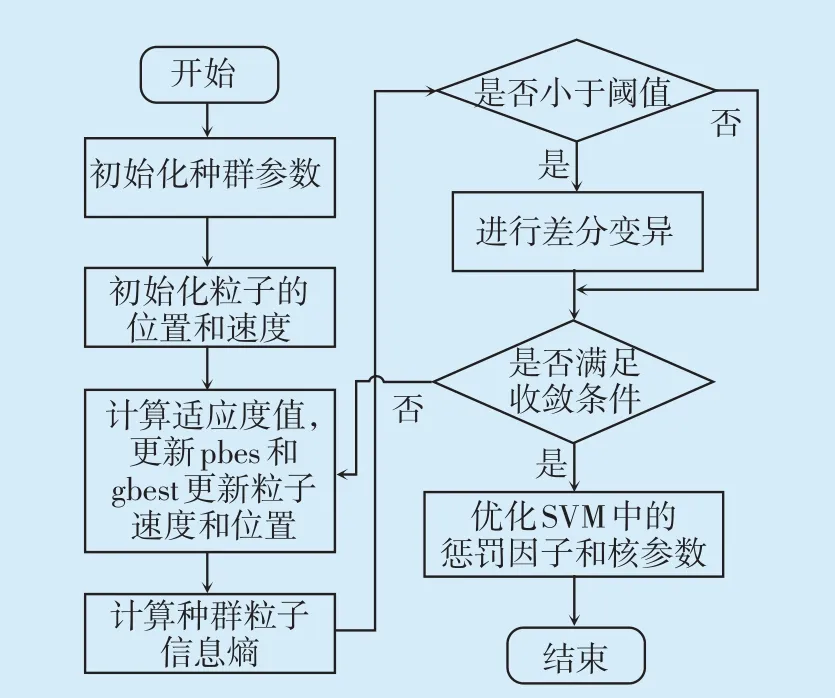
图5 改进PSO优化SVM流程图Fig.5 Flow chart of improved PSO-SVM model

由图5 可知，计算种群信息熵并与设定阈值进行对比，即可自动判断种群是否需要进行差分变异，从而避免种群重复变异，能够在提升计算效率的同时保证PSO算法不陷入局部最优解。其中信息熵的数学表达式为：

式中：U为信源符号；N为信源符号的数量；pi为不同信源符号所对应的概率。

确定变异后，在迭代前期采用DE/best/1/bin 变异策略，迭代后期采用DE/rand/1/bin策略，让算法在前期注重于全局搜索，在后期注重于局部精细化搜索。此外，改进过程中还对惯性权重因子ω做了修正。经计算，惯性权重c1从2.05减小至0.5时效果较好，而惯性权重c2从0.5 增大至2.05 时效果较好，用于修正的自适应公式如式（5）所示：

式中：c1max、c2max分别表示c1、c2的最大值，取2.05；c1min、c2min分别表示c1、c2的最小值，取0.5；t 为当前迭代次数；tmax为最大迭代次数；ωmax为最大惯性权重因子；ωmin为最小惯性权重因子。

绕组平均温度是评价电抗器工作状态的关键指标，温升趋势可以直观反映设备的运行情况。因此，本文以电抗器的电流与损耗作为输入参量，绕组平均温度作为输出变量。为验证改进PSO-SVM代理模型的预测精度，结合干式电抗器的运行工况参数，使用该模型进行不同工况下的仿真推演。仿真计算共得到90 组可以有效反映输入与输出关系特性的数据，选取75 组作为降阶模型训练数据，15组作为测试数据，对构建的降阶模型进行测试。采用均方误差和方差对误差进行判定。均方误差越接近于0、方差越接近于1，表明精度越高，降阶效果越好。训练集结果中均方误差为0.002110 1，方差为0.994；测试集结果中均方误差为8.783×10-5，方差为0.99977。由此可见，本文所建立的降阶模型具有较高的置信度。另外，还需为训练后的降阶模型选择合适的核函数，求解SVM 系数，构造相应的回归函数，根据回归函数构造输入与输出关系的响应面。改进PSO-SVM代理模型的响应面如图6所示。

图6 改进PSO-SVM代理模型的响应面Fig.6 Response surface of improved PSO-SVM model

3 干式电抗器匝间短路故障预警

3.1 故障设置

在干式电抗器实体上进行故障测试时存在实验数据难以测量，易造成经济损失等问题。在多物理场耦合模型上进行多种匝间短路故障模拟可有效避免对干抗器实体的破坏，减少经济损失，获取更完备的故障数据类型和预警划分等级。

在多物理场耦合模型中的不同位置设置不同程度的匝间短路故障，在故障模型中加入故障电流激励，分析不同故障程度下磁场沿中心轴向导线（Axial Traverse Conductor，ATC）方向和中心横向导线（Longitudinal Traverse Conductor，LTC）方向的空间分布情况。当k 层线圈发生匝间短路故障时，匝间短路故障程度（s通常为0～35%）定义如下：

式中：Hk为第k层线圈的高度；hs为短路环的高度。

磁场变化百分比用∇B来表示，定义如下：

式中：B0为磁场中的某一点正常运行时的磁场强度；Bs为匝间短路故障时的磁场强度。

为定量描述故障程度与磁场变化的关系，本文以观测点磁场变化百分比和故障程度作为变量，拟合函数关系式。故障发生时，将故障程度设置为自变量，将磁场变化百分比设置为因变量，建立故障程度预警函数，实现故障识别与预警。将故障程度预警函数简化为求解∇B和s 的拟合函数，如式（8）所示：

式中：∇BAs、∇BLs分别为沿ATC、LTC 方向的磁场变化百分比；dA为沿ATC方向的距离；dL为沿LTC方向的距离；λ1、λ2、λ3、λ4为待定拟合系数。

由干式电抗器多物理场耦合模型可知，径向第三包封附近的磁场强度变化百分比接近0，轴向则是越远离中心点位置，磁场强度越小，故一般选择第三包封的中心作为故障定位点，选择C点（沿ATC中心1 m）和E点（沿LTC中心3 m）作为测量点。设置三种故障程度，即轻度故障、中度故障、重度故障，分别对应的故障程度为0.28%、16.78%、33.29%。定义电抗器上部的1/3 为“上部”，中部的1/3为“中部”，底部的1/3为“底部”。故障发生时，沿ATC和LTC方向的磁场分布分别如图7和图8所示。

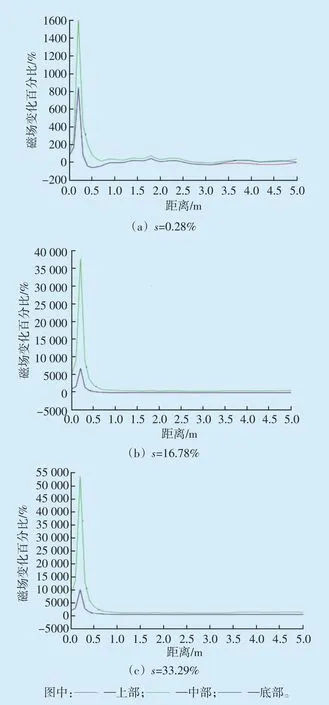
图7 沿ATC方向的磁场变化曲线Fig.7 Magnetic field variation curve along ATC direction

图8 沿LTC方向的磁场变化曲线Fig.8 Magnetic field variation curve along LTC direction

从图7可知，三种故障程度下，沿ATC方向的磁场变化百分比的最大值均大致在0.25 m处，当距离大于1 m 时，电抗器中部的磁场变化百分比大于0，上部和下部的磁场变化百分比小于0，且上部的磁场变化百分比小于下部。

从图8 可知，当故障程度为0.28%时，在LTC 方向上，干式电抗器近内壁（距离为1 m）处的磁场变化百分比大于外壁（距离为3 m）。同时，随着故障程度的增加，内外壁磁场变化百分比的差异逐渐减小。当故障程度为16.78%和33.29%时，近内壁的磁场变化百分比小于末端外壁，并且两端磁场的变化趋势基本一致。

整体来看，当电抗器同一位置发生故障时，磁场变化百分比随故障程度的增加而增大；在同一故障程度下，最内层线圈的故障对磁场的影响最大，最外层线圈的故障对磁场的影响最小。

3.2 故障程度检测函数

以上阐述了匝间短路故障程度与空间磁场变化百分比之间的关系，为了进行更直观地描述，本文将故障程度设为自变量，将磁场变化量设为因变量，建立故障程度检测函数，实现故障预警，如式（9）所示。

该式选择C点（沿ATC中心1 m）和E点（沿LTC中心3 m）作为测量点，指数拟合后获得故障检测函数表达式，相应的拟合曲线如图9所示。

图9 故障程度函数拟合曲线Fig.9 Fitting curve of fault degree function

利用多物理场耦合模型模拟其他匝间短路状态时，选取第11 层线圈中心为故障位置，短路匝数为96匝，故障程度设定为15%。仿真计算中，C点和E点处模拟的磁场变化百分比分别为483.8006%和5173.968%。由于在C点和E点上关于拟合函数的解是唯一的，因此可利用上述数据由式（9）得到故障程度计算值s′，并由式（10）求解设定值和计算值间的绝对误差e和相对误差e′，计算结果如表2所示。

表2 故障程度设定值与计算值间的误差Tab.2 Error between the set value and calculated value of fault degree

由表2 可知，采用故障检测函数计算出的s′与设定值s的绝对误差小于1，且相对误差在允许的范围内（0～8%）。因此，故障程度检测函数的准确性较高。

4 现场应用结果与分析

本文对某500 kV变电站多台66 kV并联干式电抗器进行了红外测温，测温结果如图10 所示；并对干式电抗器异常温升的红外图谱进行了分析。结果显示，匝间短路故障或由制造工艺不良造成的干式电抗器包封间距存在偏差会导致包封间温升明显增大。此外，本文还对某500 kV 变电站35 kV 并联干式电抗器进行电磁场测量与数据比对。结果显示，干式电抗器股线间若存在不规则间隙则会引起局部电磁场强度增大2～8倍。

图10 某500 kV变电站66 kV干式电抗器红外温度测量现场Fig.10 Infrared temperature measurement site of 66 kV dry reactor in a 500 kV transformer station

5 结语

本文提出一种干式电抗器的建模与故障预警方法。该方法通过建立干式电抗器电磁-电路二维分析模型计算包封损耗，通过多物理模型融合建立三维流体-温度场有限元模型，引入并改进PSO-SVM 的代理模型算法对温度场模型进行降阶处理，完成模型构建。为验证方法的有效性，在上述模型建立的基础上进行多种匝间短路故障模拟实验，进行故障识别与预警，并将该方法分别应用于某500 kV 变电站35 kV 及66 kV 并联干式电抗器的电磁场强度和温度测量。应用结果显示，本文提出的故障预警方法能够对干式电抗器的匝间短路等故障进行准确诊断与预警。