针对电力系统数据缺失的暂态电压稳定评估方法

姜鸣瞻，杨楚原，蒋何为，崔梓琪，袁铭洋，刘颂凯，张 磊

（1.国网宜昌供电公司，湖北 宜昌 443000；2.三峡大学电气与新能源学院，湖北 宜昌 443002）

0 引言

随着电网互联规模、复杂度日益增加，高比例新能源日益普及，电力系统运行的电压稳定水平接近稳定极限[1-3]，而电压稳定问题中，暂态电压失稳可能造成发电机组脱网、大范围停电等连锁反应。因此，迫切需要研究安全、快速、可靠的电力系统暂态电压稳定实时监测方法。

传统的电力系统暂态电压稳定评估（Transient Voltage Stability Assessment，TVSA）方法包括时域仿真法和能量函数法[4]，这两种方法均依赖精确的系统建模和大量的时域仿真计算，对测量数据的完整性和计算准确性要求较高，且不能实现实时TVSA，同步相量测量单元（Phasor Measurement Unit，PMU）的测量数据会随着时间的推移而积累，因此需要寻找一种能够在及时准确处理缺失数据的同时保持快速、精准的暂态电压稳定评估计算新方法[1]。

近几年，随着大数据技术的发展，基于数据驱动的人工智能方法被研究者广泛使用[5-8]。基于数据驱动的TVSA 模型有更好的学习能力，可以适应更大规模的数据量，评估速度更快。因此，数据驱动方案被认为是实现故障后实时TVSA的一种有效方法。文献[9]提出了一种故障后短期电压稳定性（Short-Term Voltage Stability，STVS）评估的时间序列形状集分类方法。文献[10]利用决策树（Decision Tree，DT）来预测电压稳定状态。然而，上述所有数据驱动的研究都假设模型输入是完整的，而实际的电力系统会由于PMU故障、通信延迟和网络攻击等问题导致测量数据丢失，进而影响现有的机器学习模型性能。考虑数据缺失的影响，文献[11]通过利用可用数据填充缺失数据，但该方法计算复杂度高，不适用于实时故障后的电压稳定评估。文献[12]中，退化决策树（Degenerate Decision Tree，DDT）使用大量的单个决策树来填充缺失数据，但其性能受到树状结构的限制。上述方法均取得了一定成果，但经模型填补后的数据误差较大，且耗时长，难以保证模型在线应用的准确性与时效性。

本文提出一种基于多视图缺失数据填充（Multi-view Missing Data Imputation，MMDI）和门控图神经网络（Gated Graph Neural Network，GGNN）的TVSA 方法，其中，MMDI 模型利用数据间的时空相关性，形成4个互补的时空视图，考虑从多个时空角度对缺失数据进行填补，修复缺失数据；GGNN模型通过修复数据集，基于图网络，提高了电力系统暂态电压稳定情况的评估精度。

1 算法介绍

1.1 MMDI

从含m 个节点的系统采集PMU 数据进行在线监测，给定采样时间Twin，采样时间间隔T，依次从各个节点上获取不同类型的PMU测量值，形成不同类型的测量矩阵X=[x1,x2,…,xm]T，xi=[xi1,xi2,…,xin] ，表示节点i（1≤i≤m）某一特征的时序测量值，n=Twin/T。

考虑构建4 个互补的时空视图，从多个时空角度对缺失数据进行填补[13]，即全局时间视图、全局空间视图、局部时间视图和局部空间视图，以X中的缺失数据x（ij1≤j≤n）为例从多个时空角度进行填补，如图1所示。

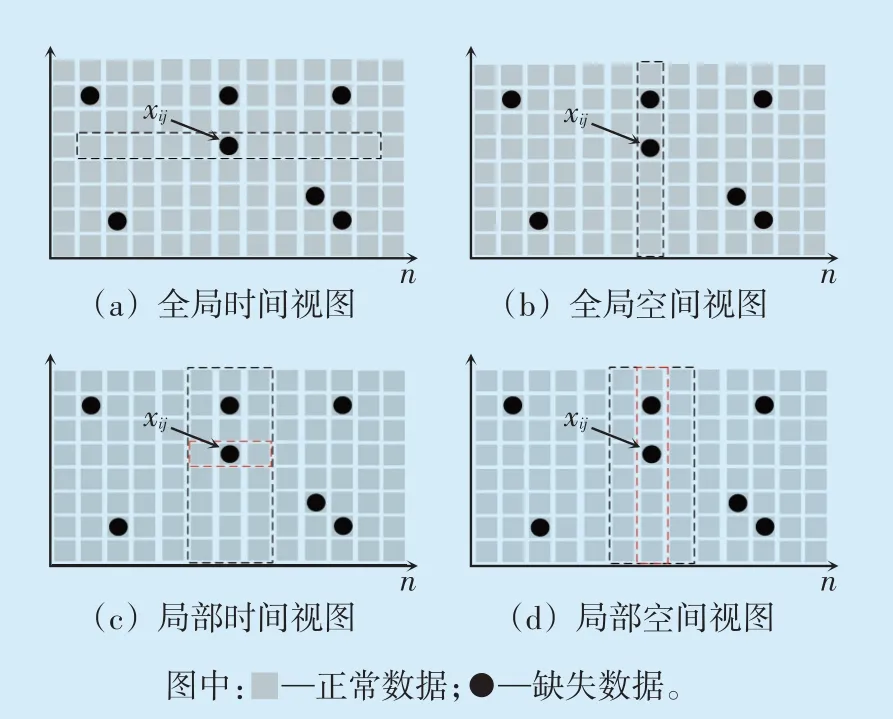
图1 多时空视图Fig.1 Multiple spatio-temporal views

（1）全局时间视图：从第i 个节点的时序测量中提取1 个以xij为中心，含有2l+1（1≤l≤n/2）个数据点的时序相邻数据点数组，如图1（a）所示，xij在全局时间视图下的估计值xij1为：

式中：xik为时序相邻数据点数组中的元素；|k-j|为xij和xik之间的时间戳差，（j-l)≤k＜（j+l）；β为衰减系数，β∈( 0,1) ；λik为判断xik是否为缺失数据点的特征函数，若xik是缺失数据，则λik为0，否则为1。

（2）全局空间视图：给定系统的导纳矩阵Y，对应的阻抗矩阵为Z。从第j 个时间戳获得系统不同节点的PMU 测量值数组，如图1（b）所示，基于逆距离加权的定义，xij在全局空间视图下的估计值xij2为：

式中：xkj为从第j 个时间戳线获得系统不同节点的PMU 测量值数组中的元素；Dki为基于Z 计算出的k、i节点间的电气距离，可以近似估计节点之间的空间相关性；λkj为判断xkj是否为缺失数据点的特征函数，若xkj是缺失数据，则λkj为0，否则为1。

（3）局部时间视图：给定1 个以xij为中心的m(2p+1) 大小的矩形窗口，如图1（c）所示。根据矩形窗中的第i行，推断出xij在局部时间视图下的估计值xij3为：

式中：S(j,k)为从时间戳j和k(j-p≤k＜j+p)获得的第i个节点测量值之间的相似性。

（4）局部空间视图：与局部时间视图类似，提取矩形窗口，如图1（d）所示，从局部空间的角度来看，通过第j列元素推导出xij在局部空间视图下的估计值xij4为：

式中：W(i,k)为节点i和k(1≤k≤m)的时序测量值之间的相似性。

基于局部时间视图和局部空间视图的缺失数据估计方法涉及数据矩阵的提取，若提取的数据矩阵中存在多个缺失数据，会导致和不够可靠。为解决上述问题，可以使用基于全局时间视图和全局空间视图的缺失数据估计方法来填补数据矩阵中存在的多个缺失数据值，直到矩阵中只存在1个缺失数据的情况为止，再将的均值作为缺失数据xij的预测填补值。

1.2 GGNN

GGNN 是一种基于门控循环单元（Gate Recurrent Unit，GRU）的经典空间域消息传递模型，通过增加门控装置可有效缓解反向传播时参数梯度消失的问题[14-16]。GGNN 通过将有固定节点的实际电力系统看作一个静态结构图网络，以节点的时序数据作为特征来实现电力系统的暂态电压稳定评估。

构造1个无向图G=(V,E)，V表示系统中的节点，每个节点由其特征和相关节点来描述，evw∈E 表示节点v 和节点w 之间的关系，可以用节点的数量和线路的长度来表示。如果节点数量和线路长度数值较大，则表明节点之间的相关性较小。GGNN 的目标是获取嵌入状态fv，fv∈Rs，包括节点v的所有相邻节点信息，是1 个s 维向量，表示节点v 的隐藏状态。fv对应的输出Ov表示节点的得分。G=(V,E)有1个图标签LG，用来表示系统的暂态电压稳定状态，每个节点对应1个描述该节点一系列特征的特征向量d，节点v的特征向量dv含有的元素为p、q、u、δ、η，分别表示节点v 的有功功率、无功功率、电压幅值、电压相角和节点v是否受扰的情况。

GGNN模型的基本递归性如式（5）—（9）所示：

式中：Mz、Mr、Nz、Nr为用于计算z和r的矩阵，z和r为更新门和复位门；σ为一个s型函数；为节点v在t时刻的相邻节点信息的向量。

式中：tanh(x)为激活函数；M 和N 分别为节点v 的相邻节点信息向量和节点v的信息向量在tanh激活函数中对应的权重矩阵。

当模型图输出时，将图的表示向量fg定义为：

最后，利用fg来评估电力系统的暂态电压稳定性，如果fg≤0.5，则令LG=0，表示系统暂态电压不稳定；否则，令LG=1，表示系统暂态电压稳定。

2 暂态电压稳定评估流程

本文提出的针对电力系统数据缺失的暂态电压稳定评估方法流程如图2所示。整个流程主要分为离线训练、模型更新和在线应用三部分。

2.1 离线训练

收集离线仿真数据后，建立包含电力系统暂态运行时各种变量的数据库。手动删除部分数据信息，重复多次，通过MMDI 来估计缺失数据的值，再通过GGNN 模型对系统暂态电压稳定状况进行评估。进行时域仿真时，通过暂态电压稳定实用判据对系统的暂态电压稳定性进行判别，建立包含母线电压幅值、母线电压相角、机端电压幅值、机端电压相角、发电机有功输出和发电机无功输出等多维特征及其对应稳定标签的样本集，80%的随机样本作为训练集，其余20%为测试集。将样本的特征部分作为GGNN 评估模型的输入，对应稳定标签作为评估模型的输出，通过对模型参数进行调整，使其性能达到最佳[17]。最后，在测试集上对模型性能进行测试。

2.2 模型更新

由于在离线训练阶段已基于多种运行工况对GGNN模型进行训练，得到一系列候选评估模型，所以当电力系统的运行工况发生改变时，首先判断改变的系统运行工况是否已被记录在数据库中，若有，则用对应的训练好的GGNN模型进行评估；若没有，则生成新的样本集，训练新的GGNN 模型，并将新的模型加入模型库中[1]。

2.3 在线应用

系统工作人员接收到实时的电力系统运行测量数据时，将数据立即发送到MMDI 中，然后再将MMDI输出的完整数据经过GGNN进行实时暂态电压稳定评估。

2.4 模型评价指标

本文采用式（11）、（12）所示的准确率ACC和漏判率LA来衡量评估模型的性能[18-20]，采用式（13）所示的均方根误差RMSE衡量缺失数据填充模型的性能。

式中：Ts和Fs为模型预测为稳定而真实标签为稳定和失稳时的样本数；Tu和Fu为模型预测为失稳而真实标签为失稳和稳定时的样本数。

式中：f(xi)为真实值；Y为预测值；N为预测次数。

3 算例分析

3.1 构造数据集

本文在PSASP 和MATLAB 仿真平台上以IEEE 39节点系统作为模型进行仿真，该系统有10台发电机、39条母线及46条交流线路，系统中的39条母线部署了PMU进行在线监控。基于系统的基准负荷，设置负荷水平以10%的增幅从80%增至120%，发电机出力随负荷波动而变化。故障设为最严重的三相短路故障，位于各母线端以及距离线路首端20%、35%、50%、65%、80%处，故障持续时间分别设为100 ms、150 ms和200 ms，仿真时长5 s。共生成5234组样本，包括3910组稳定样本和1324组失稳样本。

3.2 缺失数据填充模型性能分析

3.2.1 缺失数据填充效果

在离线训练样本集中随机选择1个样本进行说明，考虑到图像的清晰度，图3中只展示了7个随机节点电压幅值特征的曲线。

图3 含缺失数据电压波形的填充效果Fig.3 Filling effect of voltage waveform with missing data

图3（a）与图3（b）的曲线基本保持一致，表明缺失数据的预测结果与实际值的误差可能非常小。

3.2.2 缺失数据填充模型的性能对比

为验证所提填充缺失数据模型的性能，本文选取自回归滑动平均模型（Autoregressive Moving Average Model，ARMA）算法、K- 近邻（K-Nearest Neighbor，K-NN）算法[12]与MMDI 进行对比，样本集中设置不同数量的缺失数据，使用5 倍交叉验证。模型性能使用RMSE指标来表示，测试结果见图4。

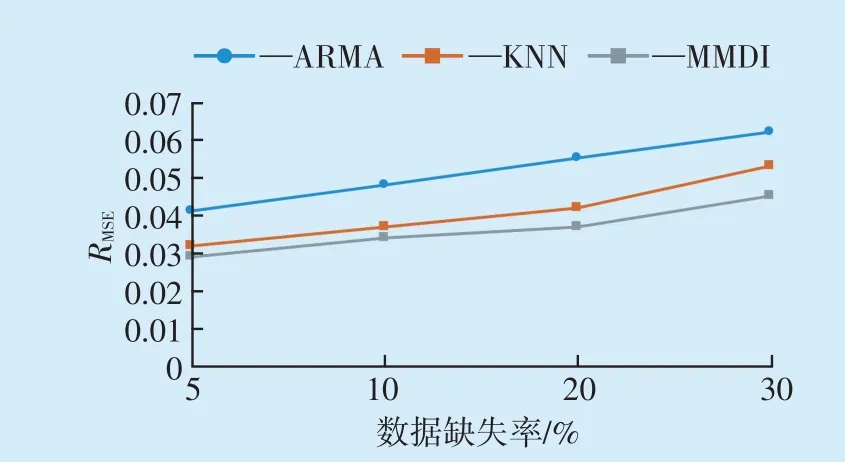
图4 填充模型的RMSE对比Fig.4 RMSE comparison of the fill model

3.3 评估模型性能分析

为验证本文所提模型进行TVSA 的性能，在同等仿真条件下使用缺失率为0%、5%、10%、20%和30%的训练数据和5 倍交叉验证，选取SVM、CNN、GRU与GGNN进行对比测试。先基于MMDI对不同缺失比例的训练数据进行填补，再将完整数据输入TVSA 评估模型，采用准确率ACC和漏判率LA来衡量模型的评估效果，测试结果如图5所示。

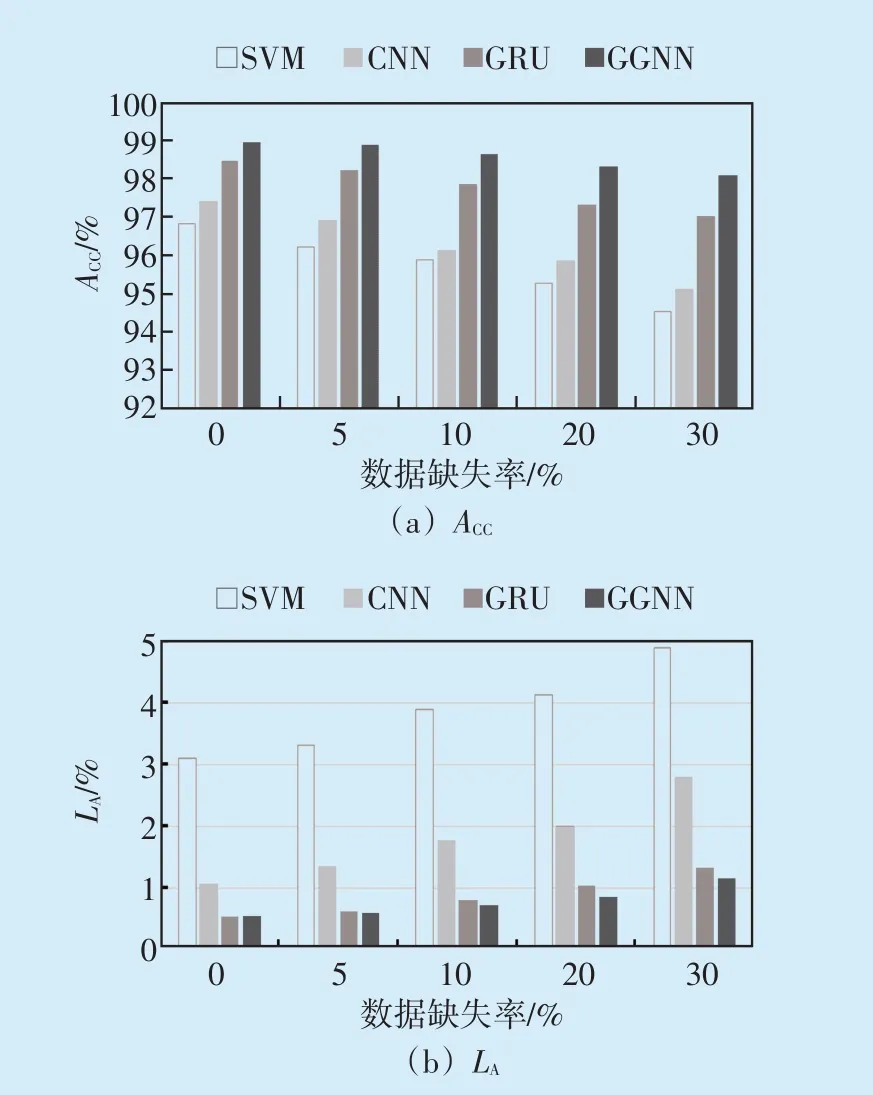
图5 不同评估模型的性能对比Fig.5 Performance comparison of different evaluation models

4 结论

本文提出一种针对电力系统数据缺失的暂态电压稳定评估方法，该方法由MMDI 缺失数据填充模型和GGNN 评估模型两部分构成。在IEEE39 节点系统中的仿真结果表明：

（1）与其他数据填补方法对比，MMDI 在不影响其他特征数据前提下，通过四个互补的时空视图完成了对缺失数据的估计，再由评估模型基于完整数据进行暂态电压稳定评估，其评估结果精度较高；

（2）与其他暂态电压稳定评估方法相比，本文提出的基于MMDI 和GGNN 模型构建的TVSA 方法既考虑了对缺失数据问题的处理，还采用具有图网络的神经网络表征系统的拓扑结构及其系统节点间的关系，使整个模型在性能方面具有显著优势。