Discreet investors exert greater influence on cooperation in the public goods game
Hong-Wei Kang(康洪炜), Zhan-Yao Jin(金展瑶), Ming-Yuan Li(李明远), Mie Wang(旺咩),Xing-Ping Sun(孙兴平), Yong Shen(沈勇), and Qing-Yi Chen(陈清毅),†
1School of Software,Yunnan University,Kunming 650000,China
2College of Information Science and Engineering,Northeastern University,Shenyang 110004,China
Keywords: public goods game,heterogeneous investment,discreet investors,cooperation
1.Introduction
Various studies have examined how to reduce free-riding behaviors.[1-3]In the traditional public goods game,[4]players are divided into cooperators and defectors.The cooperators contribute investments to the common pool,[5,6]whereas the defectors will do nothing.The total investments are multiplied by a synergy factor and then distributed equally to all players.Therefore, the cooperators improve the group payoffs, the defectors obtain larger payoffs by free-riding[2,7]and the payoffs are greater than those of cooperators.Rational players often choose to betray others.Therefore, the conflict between personal interests and collective interests leads to the tragedy of the commons.[8,9]Both in the biological world and in human society, cooperative behavior is a common phenomenon.[10-13]The evolution of cooperative behavior in social dilemmas has been constantly explored.[14-16]Based on previous work,Nowak[17,18]summarized five mechanisms to promote cooperation: kin selection,[19,20]direct reciprocity,[21-23]indirect reciprocity,[24,25]group selection[26,27]and network reciprocity.[28]In past studies,reputation,[29-33]alliance,[34,35]punishments,[36-42]rewards[43-45]and other mechanisms have been proposed to solve this problem.
Heterogeneous investment[46-48]strategies are adopted widely by individuals and firms in economic markets.In this way,the investment risk is reduced,cooperative behavior can survive effectively and it is easier for individuals to cooperate.Zhanget al.[49]proposed a spatial public goods game model with dynamic allocation of investment.Partners tend to invest more in groups more favorable to them in early rounds.Meloniet al.[50]allowed participants to redistribute their investments according to historical returns and found that the Pareto distribution of returns naturally occurred.The Pareto distribution describes the phenomenon that 80%of the wealth in society is held by the top 20%of the population.
In our work,we propose a discreet investor model whose heterogeneous investment strategies[51,52]affect the direction of evolution of the system.Researchers can introduce this information asymmetry in specific cases to explore its impact on the outcome of the game.In real life, individuals usually have some information about other players.Our discreet investors are similar to investors in an investment company.[53]In modern society, information resources are relatively easy to obtain.Investors in real life can pay a certain price to obtain credit information[54]and the criminal record[55]of the investee.The discreet investors in our model can obtain the investment behavior of their neighbors in the games.If one neighbor is a defector, the discreet investor does not invest in this neighbor.When one neighbor shows cooperative behavior, a discreet investor should also check the cooperation value of this neighbor.Based on the investment behavior and cooperation value of the neighbor, final investments are calculated for each individual.The greater the cooperation value of neighbors, the greater the final investments of the discreet investor in the common pool.Concerning the timing of the discreet investor’s information acquisition,players evolve randomly in the initial time step to simulate the initial state of the population.Subsequently,the discreet investor obtains the cooperation value information for other players starting from the second time step.This information is obtained based on the results of the player’s last round of the game.Section 2 of this paper describes the discreet investor model and method in detail.In Section 3,the results of the experimental numerical simulation and a discussion are presented.Finally, Section 4 provides our conclusions.
2.Model and method
2.1.Public goods game
In this paper,we consider evolutionary game experiments on two-dimensional regular square lattice networks.[56]The system scale is set toM=10.Each player plays in a group withNindividuals.On a square lattice, nearest neighbors of each player are four individuals,soN=5.At the end of each game,the participants in the group center imitate the strategy of the neighbor with greater payoffs with a certain probability.With the change in the strategy,the behavior of the players in the next round changes accordingly.
In the traditional public goods game, the cooperator in each group will contribute a costIcto the common pool whereas the defector will do nothing.Then, the total contributions in the common pool are multiplied by a synergy factorrand distributed equally to each individual in the group irrespective of their strategy.The payoff formula of the traditional public goods game model is as follows:
whereπcis the payoffs of the cooperator,πdrepresents the payoffs of the defector,Ncis the number of cooperators,ris the synergy factor andIc=1.
The traditional game model of public goods has only cooperators and defectors.In this paper, we add discreet investors based on the traditional model and observe the changes to the direction of evolution of the traditional model.Cooperators,defectors and discreet investors are evenly distributed in the network.A discreet investor positioned at the center can access more information,whereas a discreet investor located at the edge can only acquire limited information.The positional information indirectly influences the neighbor behaviors that the discreet investor can observe.Furthermore, a discreet investor positioned at the center wields more influence within the network, and its investment decisions might have a larger impact on other nodes within the network.Within the same group, a discreet investor at the center might emphasize the overall cooperative dynamics of the network more when making investment decisions,while a discreet investor at the edge might be less influenced by its neighbors.Therefore, within a group, as shown in Fig.1(a), when the discreet investor is a central node, the discreet investor needs to consider four neighbors when investing in the common pool.In Fig.1(b),when the discreet investor is the neighbor node, it needs to consider the central node when investing in the common pool.
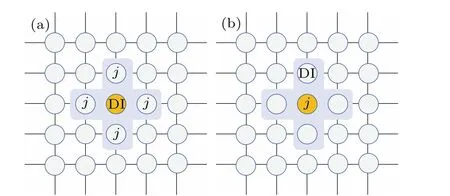
Fig.1.(a) The discreet investor (DI) is the central node of the group.(b)The DI is the neighbor of the group.
First, we calculate two kinds of expected investments based on the different positions of the discreet investors in the group.This is because a discreet investor investing in the common pool needs to consider the cooperative value of its neighbors.In Fig.1(a), the discreet investor is the central node in the group and it has to consider the cooperative value of four neighbors.In Fig.1(b), the discreet investor is at the edge of the group,and it only needs to consider the cooperative value of its direct neighbor.The expected investment of the discreet investor takes into account the number of neighbors,and there are two possible numbers of neighbors of the discreet investor within a group, so the discreet investor has different ways to invest.
The expected investment here is not the discreet investor’s direct investment to its neighbors.The discreet investor’s investment in the common pool needs to consider the cooperative value of its neighbors: the sum of the product of the discreet investor’s expected investment and the cooperative value of each neighbor is the discreet investor’s investment in the common pool.When the discreet investor is the central node in the group it hasN-1 neighbors,the total fundSDIdivided byN-1 is the discreet investor’s expected investment to its neighbors.When the discreet investor is an edge node in the group, it has only one neighbor, and the total fundSDIis the expected investment of the discreet investor to the neighbor.


A discreet investor judges the cooperative value of a near neighborjdepending on the number of cooperators and discreet investors amongj’s neighbors.Although the cooperative behavior ofj’s neighbors does not affect the discreet investor,the behavior of defectors amongj’s neighbors affectsj.Whenjimitates the strategy of defectors it indirectly affects the discreet investor.When discreet investor’s right neighborjis a cooperator(Fig.2(a)),jhas three neighbors that are defectors.In Fig.2(b)jhas three neighbors that are cooperators.jis in the process of continuous evolution due to the free-riding behavior of the defector and Fermi’s rule;in Fig.2(b),the more cooperators amongj’s neighbors,the greater the possibility of their continued cooperation.In Fig.2(a), the fewer cooperators amongj’s near neighbors, the greater the possibility of their choosing the betrayal strategy, and whenjchooses the betrayal strategy,jwill influence the discreet investor.

Fig.2.(a)The right nearest neighbor j of discreet investor DI is a cooperator (C) and all three neighbors of j are defectors.(b) The right nearest neighbor j of discreet investor DI is a cooperator and all three neighbors of j are cooperators.
Next,discreet investors need to examine the cooperation valueVjof each neighbor,so how do we calculateVjof neighbors? As shown in Fig.1,the neighbor of the discreet investor DI isj.The more cooperators and discreet investors amongj’s neighbors, the higher the payoffs ofjthe after the game,so the greater the value ofj’s cooperation.When the discreet investor’s neighborjis a defector,jis no cooperation value.The formula for the cooperation value ofjcan be expressed as
whereV(DI,j)represents the cooperation value of the discreet investor’sjth neighbor when a discreet investor is the central node of the group, as shown in Fig.1(a).V(j,DI)represents the cooperative value of the discreet investor’s only neighborjwhen discreet investor is the edge node of the group,as shown in Fig.1(b).N(j,C)andN(j,DI)represent the number of cooperators and discreet investors amongj’s neighbors in a group where the center node isj.
Therefore, the final investments invested by discreet investors in the common pool can be formulated as
whereI(DI,j)represents the final investments invested in the common pool when the discreet investor is the central node of the group,as shown in Fig.1(a).I(j,DI)represents the final investments invested by discreet investors into the common pool when discreet investors act as neighbors in the group,as shown in Fig.1(b).
The investments of the cooperators and the defectors are
In the real world,investors often need to pay costs in time and money to investigate the investment object and market environment.The cost of discreet investors assessing the cooperation value is quantified byCDI.When calculating the payoffs,we multiply the contributions of all players in a group by a synergy factorrand distribute it equally to each player in the group.We calculate the payoffs of discreet investors by subtractingCDIand the final investment,then calculate the payoffs of cooperators minus the investmentsIc.Defectors get payoffs at no cost.Therefore,after each group game,the players’payoffs are
The meaning of each parameter is shown in Table 1.
Each player participates in both a self-centered group game and a neighbor-centered group game.Therefore,the total payoffs of an individual are the sum of the income obtained by the group centered on them and the payoffs obtained by the group centered around their neighbors.The formula can be expressed as
whereΩirepresents the set of groups with individualiand its neighbors as the central nodes, andujrepresents the payoffs ofiin the corresponding group.

Table 1.Parameter table of formula(6).
2.2.Replicator dynamics
Players’different investment methods lead to inconsistent payoffs.After accumulating payoffs, all players update their strategies through the Fermi rule.The probability that playerxrandomly learns the strategies of neighboryis
whereUxandUyrepresent the total payoffs of playersxandy,respectively.krepresents the random noise(k=0.1)[57]generated by the adoption of strategies.This parameter quantifies the uncertainty of strategy adoption,which means that the strategies of players with better performance are more likely to be adopted,although the strategies of players with poor performance may also be adopted.
We simulated 104evolutionary time steps,and the experiment adopted synchronization updating.To avoid the uncertainty of the experiment,our experimental data are the average of the data from 10 experiments.
3.Experimental simulation results and analysis
We first compared three different strategy combinations forr=2,namely,the evolutionary results of cooperators and defectors (C+D), discreet investors and defectors (DI+D),and discreet investors,cooperators and defectors(DI+C+D).The results in Fig.3(a) show that in the early stage of evolution,the cooperators cannot resist the invasion of the defectors,and the proportion of cooperators decreases rapidly and finally reaches zero.In Figs.3(b) and 3(c), discreet investors dominate the evolutionary process in the system.The experimental result indicates that the heterogeneous investors effectively resist the invasion of defectors and significantly improve the cooperation level of the system.

Fig.3.For r=2,the blue line represents discreet investors,the green line represents cooperators,the red line represents defectors,the horizontal coordinate represents the time step and the ordinate represents the proportion of strategies used by the players.
To further explain why heterogeneous investment strategies affect the evolution of the system, we provide snapshots of three different sets of strategies C+D, DI+D and DI+C+D forr=2; snapshots are provided to highlight the evolution of different strategies.In Figs.4(a1)-4(a6), the cooperators briefly form cooperative clusters at the beginning but ultimately lack an effective mechanism to protect themselves from the defector’s invasion and gradually die out.In Figs.4(b1)-4(b6), where discreet investors and defectors are randomly and uniformly distributed,defectors are invaded by discreet investors, and the heterogeneous investment strategy has an overwhelming advantage.The difference between our discreet investors and our cooperators is that in the face of different investment environments,the heterogeneous investment mechanism of discreet investors can effectively prevent them from being over-exploited by defectors.The clusters formed by discreet investors are difficult for defectors to invade, and at the same time they are constantly exploring and expanding to the edges of the square grid network.We also discovered an interesting phenomenon where discreet investors cannot completely drive out defectors.Although a discreet investor does not invest in the defectors,when the four neighbors around the defector are all discreet investors its free-rider attribute makes its payoffs greater than its four discreet investor neighbors,and there are discreet investors imitating the defector’s strategy.After the newly generated defectors form tiny clusters,the average gain of defectors decreases,and the defectors at the edge of the cluster are invaded by discreet investors after the payoff decreases.In the end,defectors can only continue to form small clusters within a limited range,then they are invaded by discreet investors and form small clusters when they are going to die.This also explains why in Fig.3(b)the fraction of discreet investor strategies never reaches 1.
For the snapshots of DI+C+D,as shown in Figs.4(c1)-4(c6).In the initial state,our players are homogeneously distributed in the lattice network.This distribution state is particularly conducive to the early use of cooperative strategies by defectors.Observing the snapshots,we can see that the number of defectors increases rapidly,while the numbers of cooperators and discreet investors are decreasing.Defectors invade most areas in the square grid network, but discreet investors and cooperators benefit from each other in the network, and they survive in clusters where cooperative behavior is effective.However,after the cluster of the cooperators and discreet investors has formed, the cooperators at the edge of the cluster are constantly over-exploited by the defectors and unable to resist the invasion of the defectors,so the discreet investors ultimately dominate the evolution of the system.
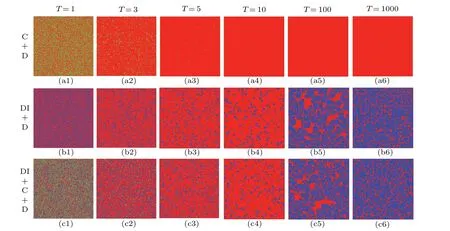
Fig.4.Snapshots of players at different time steps under the three strategy combinations(C+D,DI+D and DI+C+D)for r=2, where the blue dots represent discreet investors,the green dots represent the cooperators,the red dots represent the defectors and T refers to the time step.
The results in Figs.3 and 4 show that the heterogeneous investment mechanism of discreet investors can promote cooperative behavior in evolutionary games.To better explain the evolutionary process,we further studied the details of the relevant payoffs of the above mentioned three different strategy combinations in the evolutionary process.
Observing Fig.5(a),we can see that in strategy combinations with discreet investors,the average payoffs of all players are significantly improved, indicating that heterogeneous investment strategies can affect the direction of evolution of the traditional public goods game.In Fig.5(b), the payoff levels of defectors decrease and finally reach zero.The cooperators have been losing money,and finally the payoffs are not shown.Corresponding to the snapshot map of our C+D strategy combination in Figs.4(a1)-4(a6),the cooperators are invaded until the defectors occupy our lattice network.The decreasing number of cooperators leads to the decreasing payoffs of cooperators from cooperation.The continuous reduction of the number of cooperators leads to the continuous reduction of the average payoffs obtained by the defectors from exploiting the cooperators.In the end, the cooperators are completely expelled, and no one contributes to the common pool.Observing Fig.5(c), we can see that average payoffs of discreet investors at the beginning are higher than those of the defectors because the advantage of the heterogeneous investment strategy of discreet investors makes them much less exploited than the cooperators;instead,they can extend their evolutionary advantage.After the system evolves, the average payoff of discreet investors increases.When discreet investors form a cluster,discreet investors at the center of the cluster make a high investment in marginal discreet investors,so the payoffs of discreet investors at the edge of the cluster are greater than the payoffs of being exploited by defectors, the advantages of clusters continue to expand and discreet investors gradually dominate the evolution.Interestingly,the average payoffs of defectors decrease first and then increase.This is because when the living space of the defectors is continuously compressed,the money for exploitation is limited and the number of defectors drops sharply,so the average income of the defectors increases instead.

Fig.5.For r=2.(a)The overall average payoffs of the players at different time steps under the three different strategy combinations.(b)The average payoff curves of the cooperators and defectors at different time steps under the C+D strategy combination.(c) The average payoff curves of discreet investors and defectors at different time steps under the DI+D strategy combination.(d)The average payoff curves of discreet investors,cooperators and defectors at different time steps under the DI+C+D strategy combination.
In Fig.5(d), under the DI+C+D strategy combination,we find that the average return of the cooperators before and after 10 time steps is greater than that of the discreet investors and the defectors.Then, it decreases and disappears.Combined with snapshots of DI+C+D in Figs.4(c1)-4(c6), it is found that in the early stage of evolution,cooperators and discreet investors help each other,which slows down the speed of the invasion by defectors,and the cooperators and discreet investors form a cluster of mutual benefits.After there is no exploitative behavior within the cluster,the cooperators continue to develop great advantages and the cooperation strategy at the center of the cluster begins to spread.The average income of the cooperators becomes larger during this period, and such clusters gradually form with the cooperators as the main body.As the number of discreet investors continues to decrease,such clusters are soon invaded by defectors.In the end,the proportion of cooperators gradually becomes zero.After the cooperators disappear, their average payoff also disappears.Only the discreet investors who have formed clusters at the beginning continue to exert their strategic advantages; finally, the discreet investors dominate the evolution, the payoffs of cooperators and defectors decline and the returns of discreet investors continue to increase.This result also corresponds to the evolutionary process of the system under the snapshots of DI+C+D strategies in Figs.4(c1)-4(c6).
The above mentioned experiments were based on the simulation experiments where discreet investors did not payCDIfor heterogeneous investment.When the three strategy combinations(C+D,DI+D and DI+C+D)are compared regarding simulation evolution and all the parameter conditions are consistent,it is proved that a discreet investor promotes the cooperation of the system because of the discreet investor’s strategy advantage.WhenCDIis taken into account, the DI+D and DI+C+D combinations have an additional parameter condition ofCDIcompared with the C+D combination.Next, we describe the impact ofCDIon our experiments.
From Fig.6(a) it can be found that whenris small(2<r <3) the cooperation level of the system is extremely high.Whenris fixed,as the costCDIincreases,the cooperation level of the system decreases,indicating that the high cost reduces the cooperation level of the system.Figures 6(b)and 6(c)explain this phenomenon: as theCDIincreases,the average payoffs of the discreet investor keep decreasing,the ability to resist the invasion of defectors keeps decreasing, the number of discreet investors keeps decreasing and the cooperation level of the final system keeps decreasing.At the same time,comparing Figs.6(c) and 6(d), we can observe an interesting phenomenon.Asrcontinues to increase, the proportion of discreet investors decreases and the proportion of cooperators increases.This is because when the return on investment of the environment is high,that is whenris at a relatively high level,the cooperators under the traditional model can survive;at this time,discreet investors pay the price to understand the rational exercise of investment behavior and cooperation value of other players, so the payoffs obtained by them begin to be smaller than those of the cooperators.At the same time, in Fig.6(a),we can see that when the cooperation factorris constant, as the costCDIincreases, the cooperation level of the system is not linear.To explore the reason for this, we selected snapshots at different costs forr=3.5.
Looking at snapshots in Figs.7(a1)-7(a6) and 4(c1)-4(c6), we can see that asrincreases, the cooperators begin to have room to live.Forr=2, the discreet investors have strategic advantages and continue to expand their living space.However, when the living space of the defector is extremely small, for example when the four neighbors of a defector are all discreet investors,its free-rider property makes its payoffs greater than that of its neighbors, so the defector always survives under this condition.The cooperators are slowly invaded by the defectors and are ultimately unable to survive.Forr=3.5, although the defectors are free-riding, the payoffs of the discreet investors are always greater than those of the defectors,so the defectors can be completely expelled.In this case,the cooperators can begin to survive.In Figs.7(b1)-7(b6) and 7(c1)-7(c6), although the parameter conditions of the two sets of snapshot graphs are the same, forr=3.5 andCDI=0.3,we can observe two interesting results.The system evolved into two states, one where all are discreet investors and the other where all are defectors.For this phenomenon,we repeated the experiment 100 times: the probability of the system reaching a steady state with all of them being defectors was 6% and the probability of all of them being discreet investors was 94%.In Figs.7(b1)-7(b6),the cooperators and discreet investors form clusters at the beginning, the cooperators at the edge of the cluster are always invaded by the defectors and the discreet investors at the edge of the cluster can resist the invasion of the defectors.However, the payoffs of cluster-centered cooperators are greater than for others.Such cluster-centered cooperators keep invading discreet investors;they first evolve into cooperators as the main body and are then invaded by defectors.Only the clusters formed by discreet investors that gradually become the main body at the beginning can survive and dominate the evolutionary process.In Figs.7(c1)-7(c6),when discreet investors dominate the lattice network and keep spreading their strategies,if a small number of cooperators and defectors survive in the center of the system the discreet investors keep invading the defectors to the edge of the system,and the cooperators at the center keep invading the discreet investors.At the same time,the defectors keep invading the cooperators in the center of the system and the cooperators, as the middle layer,isolate the defectors and discreet investors.Ultimately, defectors dominate the evolutionary process.This also explains why in Fig.6(a),when the synergy factorris fixed,the cooperation level of the system is not linear with the increase in costCDI.

Fig.6.(a) The cooperation level of the system.(b) The average payoffs of the discreet investors.(c) The proportion of discreet investors.(d)The proportion of cooperators in the system.The horizontal axis represents the cost to discreet investors to obtain the investment behavior and cooperation value of their neighbors,and the vertical axis is the synergetic factor r.
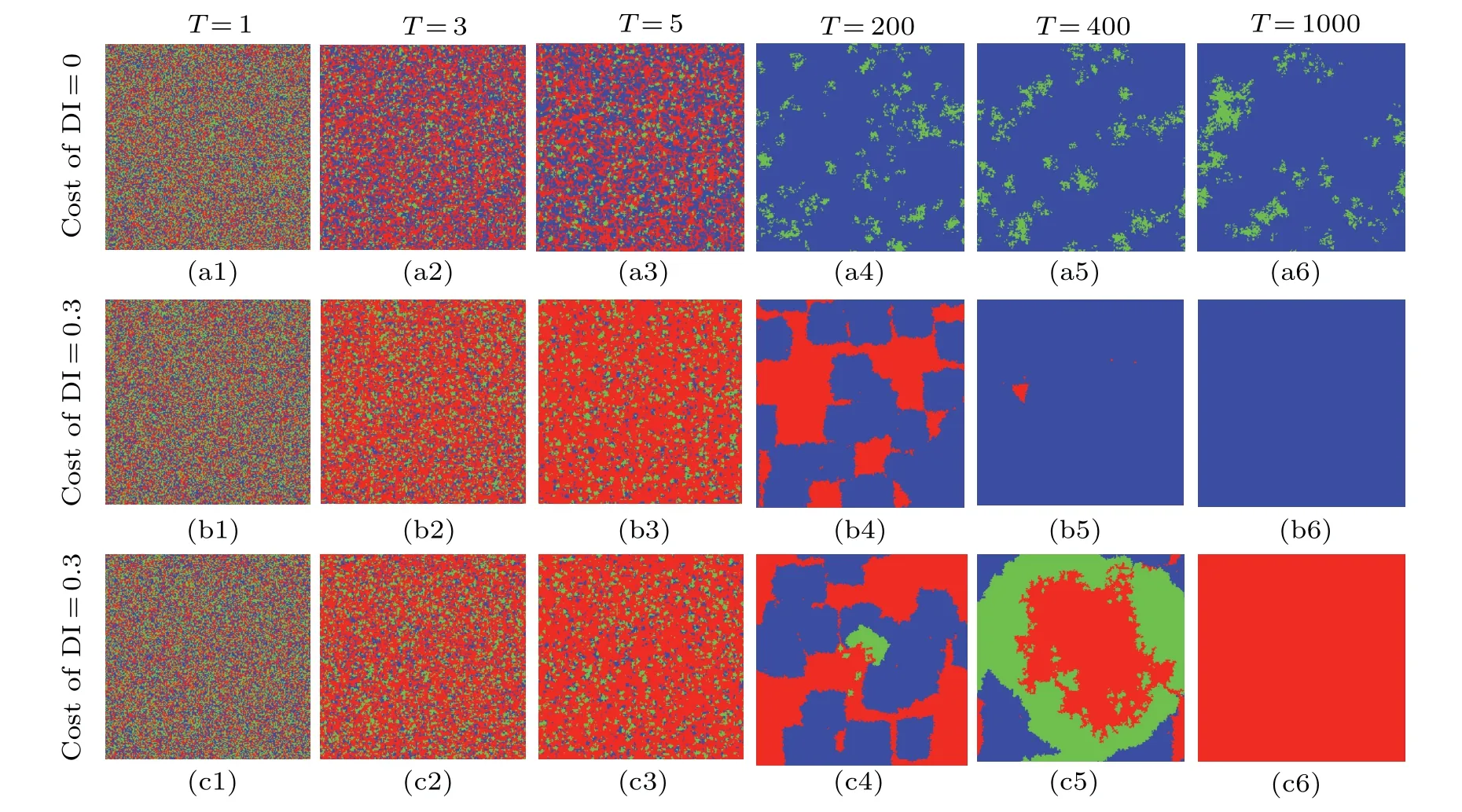
Fig.7.For r=3.5,the costs CDI are 0 and 0.3.Snapshots of the system at time steps 1,3,5,200,400 and 1000 are given under the combination of DI+C+D strategies.
4.Conclusion
How to promote collaborative behavior is a popular research topic.The sustainability of cooperation is often based on the input of participants being proportional to the return.Effective investment is also one of the ways to promote cooperation.This paper studied the evolutionary dynamics under a system where cooperators, defectors and discreet investors coexist.The difference between discreet investors and cooperators in this article is that the investment strategy of a discreet investor is heterogeneous investments while that of a cooperator is homogeneous investments.Discreet investors are more rational when contributing to the common pool.By analyzing the two parameters of synergy factor(r)and cost(CDI),we can conclude that whenris small the heterogeneous investment strategy of discreet investors is effective and spreads continuously.Whenris large, cooperators dominate the direction of evolution of the system.AsCDIincreases,the strategic advantage of discreet investors gradually disappears.The experimental results explain certain social phenomena.In an environment of low return on investments,individuals with heterogeneous investments can turn losses into profits compared with individuals who have been losing money on fixed investments.When the overall return on investment in the environment is high,altruistic behavior is encouraged and widely spread.Although the edges of a system have a strong ability to resist external intrusion and expansion,internal collapse is not dealt with in time and the system is eventually fully invaded.
Acknowledgement
Project supported by the Open Foundation of Key Laboratory of Software Engineering of Yunnan Province (Grant Nos.2020SE308 and 2020SE309).
- Chinese Physics B的其它文章
- Does the Hartman effect exist in triangular barriers
- Quantum geometric tensor and the topological characterization of the extended Su–Schrieffer–Heeger model
- A lightweight symmetric image encryption cryptosystem in wavelet domain based on an improved sine map
- Effects of drive imbalance on the particle emission from a Bose–Einstein condensate in a one-dimensional lattice
- A new quantum key distribution resource allocation and routing optimization scheme
- Coexistence behavior of asymmetric attractors in hyperbolic-type memristive Hopfield neural network and its application in image encryption

