Wave nature of Rosensweig instability
Liu Li(李柳), Decai Li(李德才), Zhiqiang Qi(戚志强),Lu Wang(王璐), and Zhili Zhang(张志力)
1School of Mechanical,Electronic,and Control Engineering,Beijing Jiaotong University,Beijing 100044,China
2Beijing Key Laboratory of Flow and Heat Transfer of Phase Changing in Micro and Small Scale,Beijing 100044,China
3State Key Laboratory of Tribology,Tsinghua University,Beijing 100084,China
Keywords: ferrofluids,Rosensweig instability,hexagon-square transition
1.Introduction
Ferrofluid is a novel stable colloidal solution composed of nano-magnetic particles and non-magnetic carrier liquids.The standard Rosensweig instability of ferrofluids is the pattern of spikes emerging on the flat surface of ferrofluids under the vertical external magnetic fieldHwith the field intensity greater than the critical fieldBc.[1-4]There is a minimum requirement for magnetizationMcunder the field ofBcfor the spikes’activation based on the theory of Rosensweig’s linear stability analysis

where the constantσandρare the surface tension and density of ferrofluids, respectively.The parametergis gravitational acceleration constant.The constantsr0,µc, andµtare relative permeabilities calculated by magnetic field intensityHand magnetic flux densityB.
According to the superposition principle of magnetic field, the critical magnetic flux densityBccan be calculated as follows:

Another interesting phenomenon is that the pattern of spikes in Rosensweig instability exhibits unique hexagonal and square patterns.[5,6]The transition of hexagon-square pattern was firstly predicted by Gailitis in 1977.[2]The possible explanation of the construction of hexagon pattern under a low field intensity is the theory of “active ring” raised by Cao.[3]The transition from hexagon to square under a large field intensity could be attributed to the magnetic flux pinning effect proposed by Kubstrup.[7]This kind of transition is thought to be controlled by energy.Nonetheless,the nature of this transition is still unclear.
In this study, the key evidence of wave-like nature of spikes are searched carefully.The control equation of Rosensweig instability is established as well as the possible solution of such an equation is raised.Regarding the theory in this research, the wave-like nature of spikes in ferrofluids is systematically discussed.The final special spikes in external magnetic field with weak field intensity are determined as cosine wave, which is corresponded to the results of linear stability analysis theory raised by Rosensweig.[1]In contrast, the form of spikes tends to be hyperbolic tangent form,which is perfectly fitted to these uniform experimental results.Based on the theoretical results,the hexagon-square transition phenomenon of Rosensweig instability is systematically discussed,which is explained by the theoretical analysis of total energy.
2.Results and discussion
2.1.Fundamental control equation of Rosensweig instability
Ferrofluids are colloidal systems, which could be regarded as a kind of uniform liquid system.Therefore, the Navier-Stokes(NS)equation is a prior equation governing the balance of body force and the movements of liquid.In additional to viscous force and gravity, the magnetic force part should be taken into consideration.It is assumed that all the changing of ferrofluids in magnetic fields are quite slow and reversible.Therefore, this“quasi-static”approximation gives a conclusion that the velocity of liquid is able to be neglected(u ≈0).[8,9]The incompressible NS equation with viscosityηcan be expressed as

The parameter is defined as a single value of altitudez=z0(x,y).
After inducing the Young-Laplace equation into the NS equation,the synthetic NS equation of ferrofluids is
whereMnis defined as the magnetization perpendicular to the ferrofluids surface,which contributes to the magnetic pressure jump of ferrofluids’surface.
2.2.Experimental equipment
The stable ferrofluids with explicit physical-chemical properties were obtained from the prior work.[10-12]As shown in Fig.1, the ferrofluids are placed into a uniform magnetic field to observe the Rosensweig instability.For the purpose of ensuring the magnetic field to be a uniform field,the large coils with iron core and currents with strong field intensity are established.The area of uniform field is as large as a circular region with a diameter of 5 cm.The field intensity of magnetic fields could be controlled by the currents in coils.The voltage and currents could be controlled by 2 external DC power supplies.The platform is kept parallel to the sea level to ensure that gravity is parallel to the magnetic field.

Fig.1.Ferrofluids in vertical uniform magnetic field established by 2 coils.
2.3.Boundary shaping and potential well model
As depicted in Fig.2, the Rosensweig instability of engine oil based ferrofluids within square-shaped boundary condition is observed.When the field intensity is lower than 12.7 mT,the spikes are not able to be established.If the field intensity is increased to larger than 12.7 mT,the spikes show up.This phenomenon proves that there is a critical fieldBc,which could be the threshold field intensity of Rosensweig instability.Another result is that the peak distribution is regular hexagon.As the external field increases to 13.5 mT, a larger hexagon distribution of spikes composed of the former hexagon and other 12 spikes are constructed.When the field intensity increases to 15.5 mT, the spikes’ distribution presents a standard square shape.This is evidence of the hexagon-square transformation phenomenon.However, the Rosensweig instability in a square-shaped container could not provide the evidence of wave-like nature of Rosensweig instability in ferrofluids.In this study, one of target is to explain the hexagon-square transformation phenomenon through energy ways.
To convince the researchers of the wave-like nature of Rosensweig instability in this study, the square-shaped container is replaced by the triangle shaped container.When the magnetic field intensity is increased to a certain valve, the spikes distribution could follow the shape of container.As shown in Fig.3, the distribution of spikes follows the shape of the container (a triangular distribution).In contrast, the spikes follow a square distribution in a square container in Figs.2(c) and 2(d).Due to this “boundary shaping effects”,the distribution patterns of spikes could be controlled by the existence of boundary.It is concluded that the Rosensweig instability could have wave’s properties (wave could shaped by boundary conditions), which is highly consistent with the finite square well model in quantum physics explained by Schr¨odinger equation.[13]The resultant wave patterns are controlled by the boundary condition in potential well, which is highly corresponded with experimental result in this study.There must be a wave explanation of spikes’distribution and existence.Therefore, the focus is casted on the NS equation of the results.

Fig.2.Rosensweig instability of engine oil-based ferrofluids within squareshaped boundary condition.Magnetic fields’ strength: (a) 12.7 mT, (b)13.5 mT,(c)15.5 mT,(d)22.0 mT.

Fig.3.Rosensweig instability of engine oil-based ferrofluids within triangle shaped boundary condition.Magnetic fields’strength: (a)14.5 mT,(b)47.0 mT,(c)69.0 mT.
2.4.Elliptical wave equation of ferrofluids
The NS equation in ferrofluids is presented as Eq.(9).Here comes a definition of average magnetization:[1]
Therefore, the interfacial pressure balance equation of ferrofluids can be written as

This equation is an elliptical partial differential equation,which contains the wave properties of Rosensweig instability that is simply constructed by continuous magnetic field and stable ferrofluids.However, it is difficult to address the issue of such a second order partial differential equation without any assumption.The results of this NS equation are largely infected by the boundary conditions.As shown in Figs.2 and 3, the infinite plane model (low magnetic field intensity), the finite square well and the finite triangular well present different types of experimental results.It is important to define the boundary condition to obtain a certain solution of this static ferrofluids NS equation.Notably, the gravity and magnetism are both forces with intrinsic energy,which could be regarded as gravitational potential and magnetic energy.
Herein, the gravity and external pressure can be defined as the potential of force casted on the ferrofluids

2.5.Perturbation of magnetic field in Rosensweig instability
To solve the NS equation of Rosensweig instability under weak magnetic field, the perturbation of the field is assumed.There is a relationship that valid permanently
If the critical condition is put into consideration, a small perturbation could result in the tiny wave of Rosensweig instability.As shown in Fig.4, the perturbation of “tiny wave” only appears under the external magnetic field intensity slightly larger than the critical field strengthHc.In this case,the height variation of spikes could be very small,which leads to an estimation based on Eq.(16)

whereA=σ,B=ρg,andC=-Em+pr.Theoretically,theCcould be regarded as constant when the external magnetic field could be regarded as approximatelyHccritical state.For positiveAandB,this second-order ordinary differential equation(ODE)has a general solution form

ParametersD1andD2are determined by the boundary conditions.If the axis is placed at the center of spikes’ patterns,the solution of spikes formF(x)is an even function according to the experimental results in Fig.2.ThenD1=D2can be obtained.
The general solution can be in the form of

2.6.Rosensweig instability with large magnetic field
The perturbation condition of external magnetic fieldH=Hc+Hperturbationreveals the wave-like nature of Rosensweig instability.However,the linear stability analysis theory could only predict the Rosensweig instability when the external magnetic field is not far greater than the critical field intensityHc.According to the experimental results in Figs.2 and 3,the critical field intensity is 12 mT-14 mT, which is fitted to the results of other researchers.[3,5]If the field intensity increases above 20 mT,the perturbation model in linear stability analysis theory is no longer applicable.It is necessary to establish a new model to illustrate the Rosensweig instability accurately in strong magnetic field.
According to Fig.5,the spikes could become very sharp(∇Zcould be very large)due to the increment of external field.In this scenario,the new estimation based on Eq.(16)can be


To verify the validation of Eq.(31), the special Rosensweig instability spikes patterns under large-field intensity are observed and compared with the computational results obtained from the theoretical results.The densityρof ferrofluids in this work is 1.346 g/cm3, the surface tensionσof ferrofluids is 30.6 mN/m,the acceleration of gravitygis 9.8 m/s2and the saturated magnetizationMsof ferrofluids is 24.5 emu/g.As presented in Fig.6,the experimental results under norm magnetic field are carefully studied.As can be seen from Figs.2 and 3, the critical fieldHcof our ferrofluids is approximately 12 mT-14 mT from results.Therefore, the applied magnetic fields strengths in these experiments are increased to be greatly larger than critical fieldHc.For a certain kind of ferrofluids,the densityρand surface tensionσare regarded as constants.It is generally believed that the magnetization of a certain kind of ferrofluids(saturated magnetizationMsis a constant)satisfied the Langevin magnetization, indicating that the magnetization only relies on the external magnetic field(M=M(H))when the temperature does not varied.[3,18]In this case, the magnetic energyEmonly depends on the external fieldH.
From the experimental results,there are 3 kinds of spikes phenomenon in this study.Figure 6(a)exhibits a kind of symmetric spikes upside and down.The central spikes exhibit symmetric sharp spikes on the top of the roof and the down floor.Firstly, it is supposed that thenλof central spikes position is 0.The side spikes next to the central spikes could have a negative or positive value,nλ(n ∈Z).If the magnetic field intensity is not large enough, the magnetic energyEmis less than the external pressurepr(Em<pr).In this case,the separation of central spikes occurs.There is another special condition that the magnetic energyEmis equal to external pressurepr(Em=pr).The opposite central double spike can be connected through a single point, which can be seen from Fig.6(b).If the magnetic energyEmis larger than outer pressurepr(Em>pr), the opposite central double spikes can be melted with each other as figure 6(c) depicted.The equation obtained is perfectly fitted to this forementioned experimental results.

Fig.5.Rosensweig instability with large magnetic field condition.
Considering the wavelength partnλin Eq.(31), there is an interesting result.If thenis enlarged from 0 to 1,the side spikes show up around the central main spike,as presented in Figs.7(a) and 7(b).It can be seen from results that the amplitudeAof side spikes is smaller than that of central spikes’amplitude.This shrinkage of amplitude of side spikes is induced by the fading magnetic field intensity from the central spikes to margin spikes(the central magnetic field intensity is larger than the margin magnetic field intensity).As depicted in Fig.7(c),the side spikes generated by the parallel magnetic field between 2 central iron cores have an amplitude shrinkage effect.From the results obtained from Figs.6 and 7,it can be concluded that the amplitude of spikes is controlled by external magnetic field energyEmand the position of wave lengthnλ.There is a prerequisite that the magnetic field intensity decreases from central position to margin.If the field intensity is even from the center to the edge,each spike can be“central spikes”.The amplitudes of spikes in this even field intensity are equal to that of the amplitude of central spikes.

Fig.6.Central spikes of Rosensweig instability with norm large magnetic fields:(a)symmetric spikes upside and down,(Em <pr);(b)funnelshaped spikes connected by 1 point,(Em=pr);(c)funnel-shaped spikes partially fused,(Em >pr).Up: experimental results.Down: Computational results.

Fig.7.Central spikes and side spikes in Rosensweig instability with norm large magnetic field condition: (a)experimental results, (b)central peaks and satellite spikes,(c)spikes with different nλ.
2.7.Energy stability of hexagon–square pattern transition in Rosensweig instability
Before considering the factors that determine the spikes’distribution patterns, it is important to determine the energy part that forms the spikes.Part of energy is the potential of repulsive magnetic forces of spikes.As shown in Fig.8(a),it is reasonable to regard a single spike as a single magnetic momentum.The potential of repulsive forces between 2 spikes is defined as[19-21]
As presented in Figs.8(b) and 8(c), the spike distribution of hexagon pattern and square pattern follow a fixed pattern.It is believed that the repulsive potential decreases along with the distance of the third power (Er∝1/r3).Herein, the spikes are regarded as on the concentric circles centered on a central spike.The spikes on the same circle have the same distancerbetween themselves and central spike.This study could introduce a constant as coefficient to this infinite series, which could have a similar form as Madelung constant.[22]Therefore, the magnetic repulsive potential can be added on same circle and evaluate it by several constantsβn


Table 1.The magnetic repulsive potential constant βn.
Except for magnetic repulsive potentialEr,the formation of magnetic spikesEfand formation of external magnetic fieldEhare essential parts of energy:
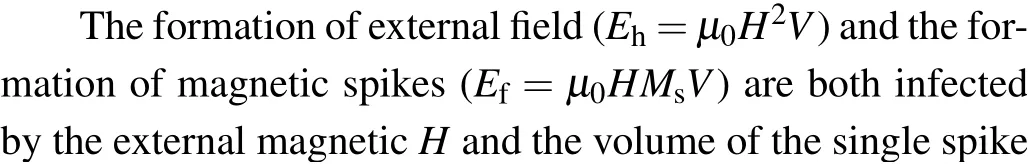


The equation of spike surface is presented in Eq.(24).The amplitudeAof a single spike could be defined as[3,8,23]
Based on these studies, the constantsa,b, andeare defined asa=0.00265,b=0.00293, ande=3.15×10-4,[3,8,23]respectively.According to the experimental results, the critical magnetic inductionBcis defined as 13 mT.The relative permeabilityµrof ferrofluids is persistently estimated as 1(1<µr<1.05).Therefore,the magnetic field is limited by the magnetization of ferrofluids.The approximation in Eq.(36)frequently applies.The total energyEtotis the sum of magnetic repulsive energyErand formation energy of spikesEfand external fieldsEhis
According to the results in Eq.(24), the total energy in hexagon spikes distribution pattern and square spikes distribution pattern can be obtained.(The densityρof ferrofluids in this work is 1.346 g/cm3.The surface tensionσof ferrofluids is 30.6 mN/m.The acceleration of gravitygis 9.8 m/s2.Saturated magnetizationMsof ferrofluids is 24.5 emu/g).As shown in Fig.9(a), the results of the total energy of a single spikeEtotin Rosensweig instabilityversusmagnetic fieldHin perturbation of magnetic field are obtained.Considering the perturbation field results,the total energy of hexagonal pattern is greater than that in square pattern.It is indicated that the energy used to construct spikes in hexagonal pattern is larger than constructive energy in square pattern.The part of contribution of repulsive potential is about 1 orders of magnitude smaller constructive energy of spikes.The hexagonal pattern has a denser packed-form of distribution than the square pattern,which ensures the hexagonal pattern become the final pattern with spikes’distribution under small perturbation field intensity.
In contrast, the Rosensweig instability with large magnetic field has a different control equation in Eq.(31).The wavelengthλand amplitudeAcould be largely affected by the strength of external magnetic field.The calculation results of the total energyEtotare summarized by Eq.(37).As depicted in Fig.9(b),the spikes patterns of Rosensweig instability under large magnetic field intensity are more complex than that under small perturbation field intensity.It has the same hexagonal patterns under compared weak magnetic field.As the magnetic field intensityHraises, the magnetic repulsive potentialErgradually becomes the main contribution to total energy of a single spikeEtot.There is a cross point between the total energy of a single spikeEtotof hexagonal patterns and square patterns,namely,hexagon-square transition point.When the field intensityHis larger than that of the transition pointHt,the spikes of Rosensweig instability exhibit standard square patterns.This is perfectly corresponded with the experimental results.
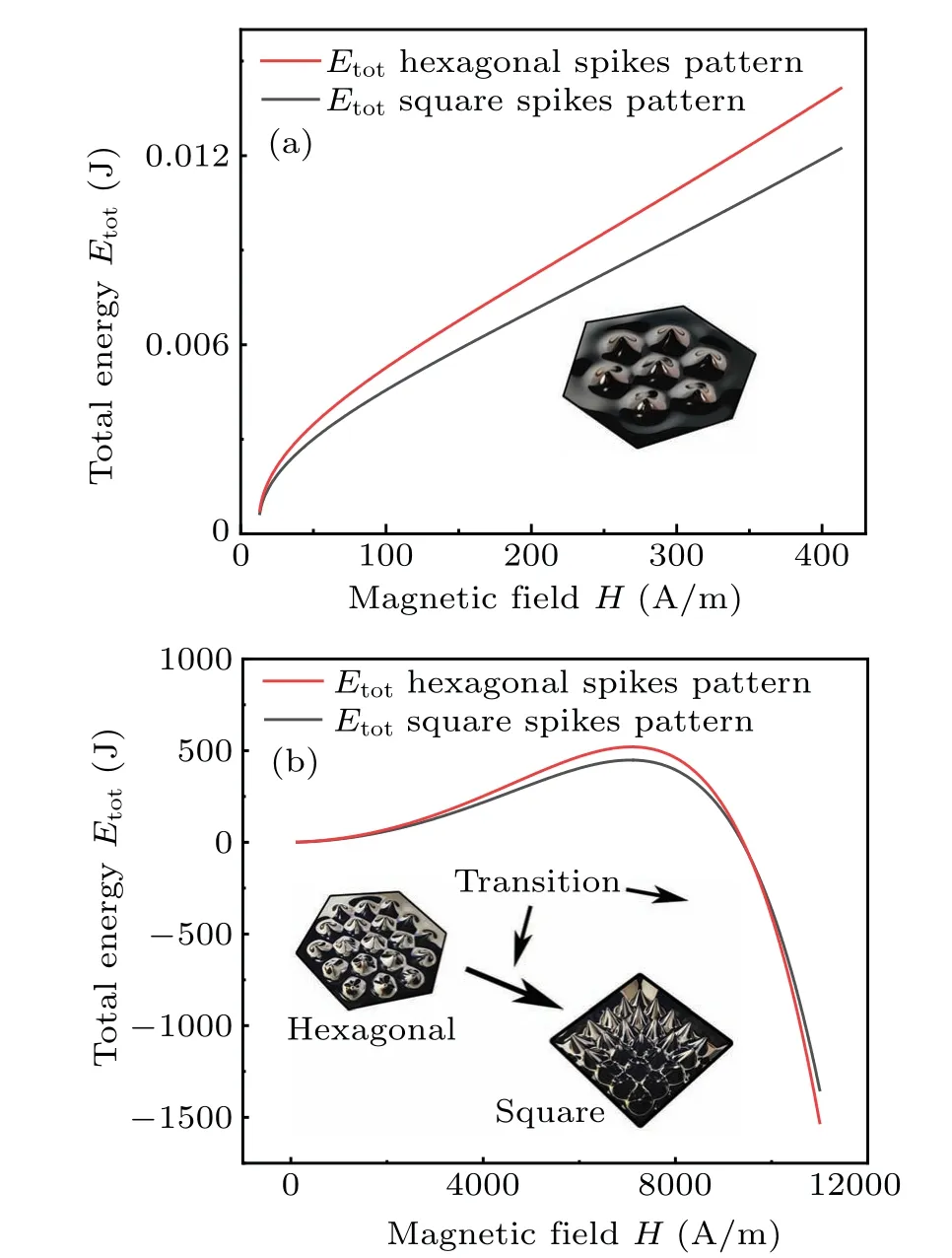
Fig.9.(a) Total energy of a single spike Etot in Rosensweig instability versus magnetic field H in perturbation of magnetic field, (b) total energy of a single spike Etot in Rosensweig instability versus magnetic field H with large magnetic field strength.
3.Conclusions
Rosensweig instability is a kind of mysterious phenomenon that has been discussed for many decades.In this study, the control equations of Rosensweig instability spikes are systematically discussed.Based on the NS equation, a standard elliptical equation of Rosensweig instability spikes is constructed, providing a conclusion that the spikes of Rosensweig instability have some nature of wave property,which is corresponded with the experimental results that the spikes’pattern can detect the container wall and spread evenly in the container.It is difficult to solve this NS equation directly.Inspired by the linear stability analysis theory proposed by Rosensweig, the magnetic field intensity could be divided into 2 parts.The perturbation part NS equation that has been solved gets a similar conclusion (cosine wave solution in Eq.(24)of the linear stability analysis theory raised by Rosensweig.However,the perturbation results are only suited for field intensityHclose to critical intensityHc(~13 A/m).Herein, this study has established a large field hypothesis to solve the other part that cannot be easily solved by perturbation model.Based on such a model, a final hyperbolic tangent form of solution of wave Rosensweig instability spikes is obtained, which is presented as Eq.(31).For the purpose of evaluating the accuracy of the equation, this study compares the results of experimental results of central spike and side spikes and theoretical results predicted by the hyperbolic tangent form of solution in Figs.6 and 7.The theoretical results are well fitted to the experimental results,which indicates that the spikes of Rosensweig instability have a hyperbolic tangent form when the magnetic field is greatly larger than the critical strengthHc.By introducing the hyperbolic tangent form model, this study successfully explaines the nature of hexagon-square transition of spikes theoretically.When the magnetic field intensity is less than the field intensity of transition point, the high efficiency of hexagonal close packing of spikes brings higher energy to construct the spikes with same field intensityHcompared with the square pattern of spikes distribution.As the field intensityHincreases to larger than transition field intensityHt, the repelling potentialErbecome the main obstacle for spikes’ pattern construction in Rosensweig instability.The hexagon-square transition is successfully explained through these theoretically results.This theoretical model results could be further adopted to explain other phenomenon of Rosensweig instability in future.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant Nos.51735006, 51927810, and U1837206) and Beijing Municipal Natural Science Foundation(Grant No.3182013).
- Chinese Physics B的其它文章
- A multilayer network diffusion-based model for reviewer recommendation
- Speed limit effect during lane change in a two-lane lattice model under V2X environment
- Dynamics of information diffusion and disease transmission in time-varying multiplex networks with asymmetric activity levels
- Modeling the performance of perovskite solar cells with inserting porous insulating alumina nanoplates
- Logical stochastic resonance in a cross-bifurcation non-smooth system
- Experimental investigation of omnidirectional multiphysics bilayer invisibility cloak with anisotropic geometry

