Comparative study on phase transition behaviors of fractional molecular field theory and random-site Ising model
Ting-Yu Liu(刘婷玉), Wei Zhao(赵薇), Tao Wang(王涛), Xiao-Dong An(安小冬),Lai Wei(卫来),†, and Yi-Neng Huang(黄以能),2,‡
1Xinjiang Laboratory of Phase Transitions and Microstructures in Condensed Matters,College of Physical Science and Technology,Yili Normal University,Yili 835000,China
2National Laboratory of Solid State Microstructures,School of Physics,Nanjing University,Nanjing 210008,China
Keywords: phase transition,molecular field theory,Ising model,Monte Carlo
1.Introduction
Although there is some overlap in time,the theoretical explorations of the phase transition for ferroelectricity,ferromagnetism,etc.can be divided into two main stages.The first one(approximately 1908-1975) mainly focuses on macroscopic crystalline materials with uniform distribution of components(commonly referred to as homogeneous systems).Specifically,all elements(atoms,molecules,ions,etc.) have the periodicity in spatial distribution on the crystal lattice or symmetry of space translation,such as barium titanate[1,2]and potassium dihydrogen phosphate[3,4]of ferroelectrics, as well as iron and nickel[5,6]of ferromagnets.While the second stage(approximately 1954 to now) mainly focuses on the macroscopic crystalline materials of component heterogeneous distribution, specifically the random distribution of some kinds of elements on the crystal lattice(no symmetry of space translation), also known as the crystals of component random distribution, such as lead magnesium niobate[7-10]and barium zirconate titanate[11,12]of ferroelectrics (including relaxorferroelectrics and dipole glasses), as well as gold iron,[13]bismuth manganese scandate[14,15]of ferromagnets(including relaxor-ferromagnets and spin glasses),etc.[16-20]
After the first stage of researches, a gradually mature theoretical system for ferroelectric and ferromagnetic phase transitions in the crystals of uniformly distributed components has been established, including the phenomenological theories (Weiss molecular field theory,[21,22]Landau theory,[23]Devonshire theory,[24-26]etc.), and the microscopic models(Ising model,[27]Heisenberg model,[28]etc.) as well as the corresponding solution methods (Weiss mean field,[22]Bethe mean field,[29]matrix transformation,[30,31]Wilson momentum space renormalization group theory,[32]and Kadanoff position space renormalization group theory[33]).
Although some research progress of the crystals of component random distribution has been made in the second stage, there are still many unsolved problems.For example, in terms of microscopic model and solution method studies, random-site Ising model,[34,35]random-site Heisenberg model,[35]random-bond Ising (Edwards-Anderson)model,[35,36]random-bond Heisenberg model,[35]etc.have been proposed,but the advances in solving the models are extremely limited so far,for these models have no spatial translation symmetry,the renormalization group method,which is extremely effective for systems with component uniform distribution,is no longer applicable.At present,there are mainly the replica method to the random-bond Ising model[35,36]and spin-string mean-field method to the random-site Ising model[37](it seems that this method is also effective for the random-site Heisenberg model).As for the researches on phenomenological theory,Kuehn and Kliem[38]proposed the fractional molecular field theory (FMFT), which seems to be related to the mesoscopic fractal structures[39,40]formed by the random distribution of components on crystal lattice.However, the effectiveness of this theory still needs to be further verified.
To solve this problem, this paper first briefly introduces FMFT,then uses Monte Carlo method(MC)[41-43]to simulate the phase transition behaviors(specific heat and susceptibility versus temperature)of the two-dimensional(2D)random-site Ising model(2D-RSIM),[35,37]and detailed comparative studies of the behaviors of FMFT and 2D-RSIM are conducted.
2.Fractional molecular field theory
The basic assumptions of FMFT[38]are made below.(i)Like Weiss molecular field theory, any pseudospin (magnetic or electric dipole)in a crystal of component random distribution is approximated as an Ising spin(σ=1 or-1),and(ii)the interaction energy between an Ising spin in the crystal and the other is-JFηγσ,whereη ≡〈σ〉is the thermodynamic statistical average ofσsuch as blow,JFthe interaction energy constant independent of temperature(T),andγa fractional factor(0<γ ≤1)also independent ofT,which is the reason why it is called FMFT.Therefore,in an external static fieldB(whenBdenotes magnetic field or electric field, then corresponding dipole is magnetic or electric dipole, respectively) along the Ising spin direction,the Hamiltonian(ℋF)of an Ising spin in the crystal is

The order parameter(ηs), i.e., reduced spontaneous magnetization or polarization of the crystal is obtained from Eq.(3),specifically,it is expressed as
The internal energy(U)and specific heat(C)per spin without external field are given below:
In addition, according to Eq.(3), the static susceptibility (χ)per spin is
whereµ0is the vacuum permeability.
Figure 1 shows the curves of calculatedC,χ,andηsversus reduced temperature (kBT/JF) by FMFT (Eqs.(4)-(7)).Forγ= 1, FMFT is simplified into Weiss molecular field theory.[21]At this point,Candχexhibit sharpλ-type peaks,and the peak temperature(Thc)of theCpeak is the same as that of theχpeak(Tsc).ηsfirst slowly,then rapidly decreases withTincreasing,and to 0 atThcandTsc.Asγdecreases: (i)theCpeak andχpeak become diffuse and gradually flatten;(ii)Thcmoves to low temperature,butTscfirst to high temperature and then to low one(Fig.3),and(iii)ηsfirst slowly,then rapidly,and slowly decreases again asTrises.
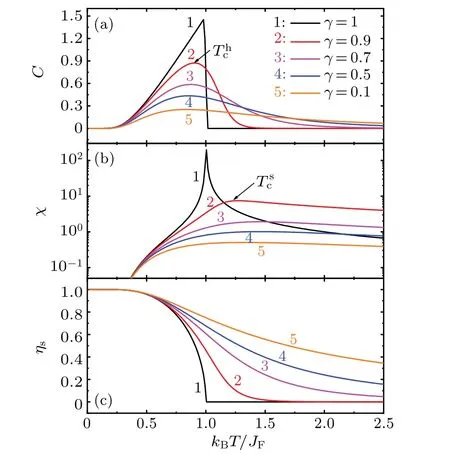
Fig.1.Curves of specific heat(C),susceptibility(χ),and order parameter (ηs) per spin of fractional molecular field theory versus reduced temperature(kBT/JF)for γ =1,0.9,0.7,0.5,and 0.1,respectively.
Mathematically,γ=1 is for the case of the second-order phase transition,andηs=0 above the transition temperature.But whenγ <1,ηs̸=0 at high temperatures becauseηγs>ηs,i.e.,ηsexpands to a high temperature region and exhibits a diffuse phase transition.Physically,γ <1 corresponds to the fractional feedback of the molecular field,i.e.,percolation effect,phenomenologically,which leads to the dispersion of the transition process.
3.2D random-site Ising model and Monte Carlo simulation
The Hamiltonian(ℋ)of 2D-RSIM[35,37]is

In addition, the above spin system is in a heat bath ofTwith which energy can be exchanged,that is,the spin system and the heat bath combine to form a canonical ensemble.[35,37]
When the model system is at thermal equilibrium,based on Boltzmann-Gibbs statistics,[35]the averageC,ηs, andχper spin are

where{σ}represents the sum of all spin states (σi,j=1 or-1)in the system,andβ ≡(kBT)-1.
According to Eqs.(9)-(10),in principle,C,χ,andηsof 2D-RSIM at thermal equilibrium can be calculated exactly,but as mentioned above, their exact solutions have not been obtained so far.The simulations ofC,χ,andηsof 2D-RSIM by using the MC method and the simulated results are provided in the following.
According to Boltzmann-Gibbs statistics,when calculating the thermodynamic parameters such asCandχof the Ising model,a certain spin-orientation configuration of the model is defined as a spin-orientation system, and the set of all such different systems is called a spin-orientation ensemble(SOE).Therefore, in the calculation of these parameters, only SOE needs to be statistically averaged.[30]However,when calculating the parameters of random-site Ising model,it is also necessary to consider the site distributionrφ i,jof spins on lattice,i.e.,not only does it require statistical averaging of the SOE with a certain site distribution,but also statistical averaging of spinsite distribution.[35,37]Here,the set of SOEs with all spin-site distribution is collectively referred to as spin-site superensemble.The specific MC simulation[43]of this superensemble is as follows.
(I)Selection of simulated lattice size
Because a macroscopic crystal contains a huge spin number, it can often be regarded as an infinite system.However,when simulating it, only a finite system can be selected due to limitations in computer memory and runtime.This work simulates a 2D-RSIM with a selected spin number of 2002,i.e.,.Due to the inevitable existence of boundaries in a finite system, we select a free boundary condition,which means that there is no interaction between the spins at the boundaries and the outside of the simulated system.
(II) Simulation of random spin distribution on a lattice

(III)Processing ofB →0
In this work,we takeB=0,and due to the possible multidomain formation in the simulation system,[31,43]the obtainedηsmay not be reliable,so it is not given here.
(IV)Simulation of spin flipping
Herein we select the Glauber dynamics of the spin flip,[35,37,43,44]i.e., the transformations in different spinorientation systems are caused by the single spin flipping,and the probability of achieving a flip fromσi,jto-σi,jduring each attempt is
whereFi,jis the local field ofσi,j,and
The simulation process of a single spin flip involves a random numberrbetween 0 and 1,which is generated by the random number function,and the spin flips forp >rbut not forp ≤r.Here, we choose that all spins in the system successively attempt to flip once as one MC step.
(V) Simulation of thermal equilibrium of spin–orientation ensemble

Because a canonical ensemble is simulated in this work,[35,43]we chooseℋlkthat varies withkas the criterion parameter of thermal equilibrium.Specifically,if the average value ofℋlkwithin a certain step interval is nearly unchanged withk,it is considered that the simulated system tends to thermal equilibrium.
Due to the fact that this work focuses on simulating the phase transition characteristics of 2D-RSIM,i.e.,the temperature range studied is near the phase transition,and the simulation results show that afterk >103, the systems substantially tend to thermal equilibrium.Here, the MC step(kE) selected to reach thermal equilibrium is 30000, and the total MC step(kF)is 35000.
(VI) Simulation of thermodynamic parameters of spin–orientation ensemble

4.Comparison of FMFT predictions and 2DRSIM simulations
TheγandJFin FMFT are the parameters which affect the peak height and peak position ofCandχ, respectively.Among them,γcontrols the height of the peak: the larger the value ofγ,the higher the peak height is;whileJFregulates the peak position: the larger the value ofJF, the higher the peak position towards high temperature is.
Figure 2 shows the fitting ofCandχversusTby FMFT to the simulation results of 2D-RSIM,with black squares representing the case ofφ=0.9 andn=211;red circles are the case ofφ=0.8 andn=224; blue diamonds are the case ofφ=0.7 andn=239, magenta stars are the case ofφ=0.6 andn=258).Figures 2(a)and 2(b)represent the preferential fits toC(Fig.2(a)) of 2D-RSIM by FMFT, with black solid line denoting the case ofγ=0.99 andJF/J=2.00; red solid line the case ofγ=0.86 andJF/J=1.80; blue solid line the case ofγ=0.70 andJF/J=1.65;magenta solid line the case ofγ=0.55 andJF/J=1.50),and thenχis calculated by the correspondingγandJF/J(Fig.2(b)).While figures 2(c)and 2(d)are those of preferential fits toχ,with black solid line referring to the case ofγ=0.995 andJF/J=1.90;red solid line the case ofγ=0.993 andJF/J=1.58;blue solid line the case ofγ=0.980 andJF/J=1.20; magenta solid line the case ofγ=0.950 andJF/J=0.75).
Figure 2(a) shows that FMFT performs poorly in fitting theCpeak shape of 2D-RSIM withφ= 0.9, but asφdecreases,the fitting becomes better and better.However,for the same values ofγandJF, the calculatedχhas significant deviations from the 2D-RSIM simulation results, including significantly higherTsc, different peak shapes, and 1-2 orders of magnitude smaller peak heights(Fig.2(b)).
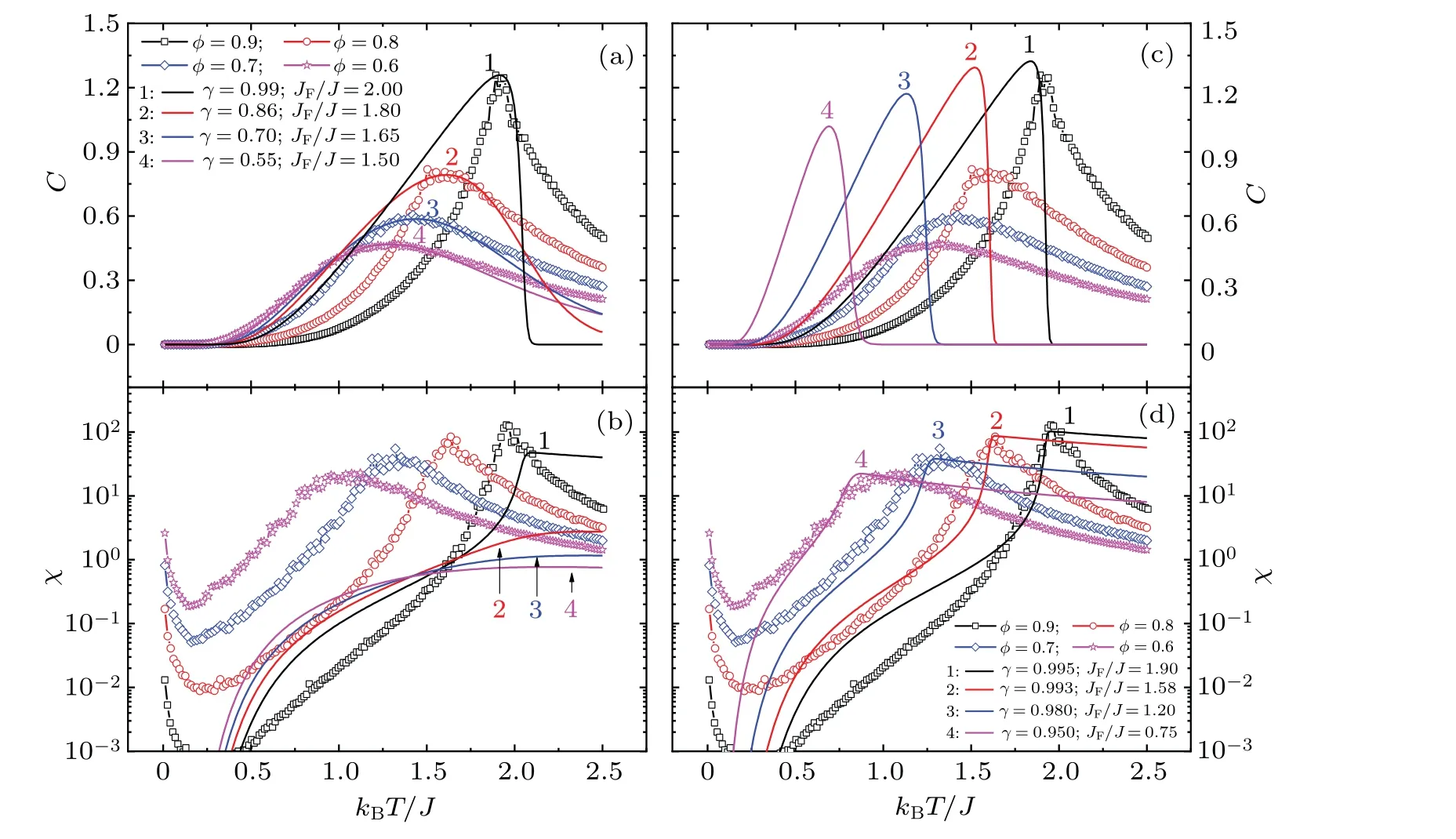
Fig.2.Fitting to simulated specific heat(C)and susceptibility(χ)results(symbol)of the 2D random-site Ising model versus temperature(T)by the fractional molecular field theory(solid line),where panels(a)and(b)represent the preferential fits to C,while panels(c)and(d)to χ.
Figure 2(d)shows that although FMFT fits well toTscand theχpeak height of 2D-RSIM, it has a poor fit to the peak shape, mainly manifested by large deviations from the hightemperature side.For the same values ofγandJF, the calculatedCnot only lowersThcand increases peak height significantly, but there is also a noticeable difference in peak shape(Fig.2(c)).
Figure 3(a)indicates thatThcandTscare equal forγ=1,and with decreasingγ: (i)Thcdecreases rapidly in the range of 1-0.9,and then slowly in 0.9-0.1,and(ii)Tscrapidly increases to its maximum between 1 and 0.6,and then slowly decreases in the range of 0.6-0.1, but keeps higher than that forγ=1.In Fig.3(b),it can be seen that whenφis greater than 0.8,Thcalmost coincides withTscof 2D-RSIM and decreases withφdecreasing.However, there is a bifurcation betweenThcandTscwhenφis less than 0.8, and comparing withTsc, the decreasing trend ofThcis slower withφdecreasing.
When comparingThcandTscof FMFT and 2D-RSIM,it is usually thought thatγ=1 in FMFT corresponds toφ=1 in 2D-RSIM.Some results can be seen from Fig.3 as follows.(i)Thcof 2D-RSIM first decreases rapidly and then slowly withφdecreasing, which is consistent with the change trend of FMFT;(ii)Tscof 2D-RSIM goes down withφdecreasing and is always lower than that forφ=1,whileTscof FMFT shows a trend of first increasing and then decreasing withγdecreasing, and is always greater than that forγ=1.This is one of the main differences between FMFT and 2D-RSIM.

Fig.3.(a) Peak temperatures of specific heat (Thc ) and susceptibility(Tsc) versus fractional factor (γ) of fractional molecular field theory.(b) Thc and Tsc versus spin concentration (φ) for 2D random-site Ising model.
The main reason for the significant deviations of FMFT from 2D-RSIM(Figs.2 and 3)is as follows.(i)Because 2DRSIM is a typical component non-uniform system,[34,35,37]its real order parameter must be spatially heterogeneous[39,40,45]and has no symmetry of space translation.However,the basic assumption of FMFT(Eq.(1))“eliminates”this spatial heterogeneity and restores the symmetry of space translation;and(ii)due to the random distribution of spins in the RSIM model,the interaction experienced by each spin is stochastic.However,FMFT averages this interaction, ignoring the corresponding random fluctuations.This is also the main reason why the introduction of local order parameter,[37]i.e.,the spatial nonuniformity considered,can achieve more accurate descriptions to the random-site Ising model.
5.Summary
This article compares the phase transition behaviors of FMFT with the simulation results of 2D-RSIM.The findings are as follows.(i)When FMFT is used to preferentially fitCof 2D-RSIM, the correspondingχhas significant deviations,manifested as significantly higherTsc, different peak shapes,and 1-2 orders of magnitude smaller peak heights.(ii)When fittingχpreferentially,the high-temperature side ofχdeviates significantly, and the corresponding deviation ofCis greater,including obviously lowerThc,higher peak height,and significant differences in peak shape.(iii) Especially whenγdecreases from 1 to 0,the predictedTscof FMFT is always higher than that forγ=1,which has opposite tendency to the results of 2D-RSIM(whereTscalways decreases withφdecreasing).In summary,the fitting accuracy of FMFT to 2D-RSIM is relatively low, and the main reason is that 2D-RSIM is a typical component non-uniform system,its real order parameter is spatially heterogeneous and has no symmetry of space translation,but the basic assumption of FMFT(Eq.(1))smooths out the spatial heterogeneity and restores the symmetry of space translation.
Data availability statement
The data that support the findings of this study are openly available in Science Data Bank at https://doi.org/10.57760/sciencedb.13807.
Acknowledgements
The authors thank Prof.Zhang Li-Li and Zhou Heng-Wei for inspiring discussion.
Project supported by the Open Project of the Key Laboratory of Xinjiang Uygur Autonomous Region, China (Grant No.2021D04015) and the Yili Kazakh Autonomous Prefecture Science and Technology Program Project, China (Grant No.YZ2022B021).
——王涛
- Chinese Physics B的其它文章
- Does the Hartman effect exist in triangular barriers
- Quantum geometric tensor and the topological characterization of the extended Su–Schrieffer–Heeger model
- A lightweight symmetric image encryption cryptosystem in wavelet domain based on an improved sine map
- Effects of drive imbalance on the particle emission from a Bose–Einstein condensate in a one-dimensional lattice
- A new quantum key distribution resource allocation and routing optimization scheme
- Coexistence behavior of asymmetric attractors in hyperbolic-type memristive Hopfield neural network and its application in image encryption

