考虑出力特性的光热参与电力平衡容量研究

孙 沛, 赵 亮, 田宏梁, 项 丽, 杨攀峰, 师 文, 秦博宇

(1. 中国电力工程顾问集团西北电力设计院有限公司, 陕西 西安 710075;2. 国网宁夏电力有限公司, 宁夏 银川 750001; 3. 西安交通大学电气工程学院, 陕西 西安 710049)

1 引言

电力电量平衡是电力系统规划运行的基础工具。其主要研究内容为评估发电系统的充裕度、计算各类电源的利用情况、发电机组检修计划的安排、确定系统备用等,进而实现水、风、光、煤等资源的优化利用[1-6]。

针对电力电量平衡,许多国内外的学者已经进行了深入的研究工作,文献[7,8]提出逐次切负荷法,文献[9,10]采用随机生产模拟计算平衡结果,文献[11,12]提出采用剩余容量日利用小时控制法等。逐次切负荷法主要是在日负荷曲线上通过平移水电工作位置计算其累计电量来安排水电机组所带负荷,剩余的负荷留给火电,并让火电带的负荷尽可能地平稳。随机生产模拟法考虑了机组的强迫停运和负荷的波动性,在持续负荷曲线上进行生产模拟,以概率性的指标来表述电力电量平衡结果。剩余容量日利用小时控制法根据各个电站的可用容量日利用小时(日发电量与可用容量的比值)由高到低的顺序安排水电机组,避免了人为指定电站顺序造成电量分配不公的问题。还有学者通过优化算法,采用机组组合和优化调度模型,求解电力电量平衡问题[4,13-16]。

为了应对日趋紧张的气候变化问题,我国提出了碳达峰和碳中和的战略目标[17-19]。在实现“双碳”目标的过程中,需要大力发展新能源发电技术。太阳能热发电技术(Concentrating Solar Power,CSP)基于其清洁、调节性能好等特点,在系统中逐步受到重视,近年来在全球迅速发展,预计2050年全世界光热发电量可能占全球总发电量的11.3%[20-23]。光热发电在我国也得到大力发展[24]。

伴随光热发电的大力发展,光热装机占比逐步升高,如若不考虑光热的容量效益,可能导致在规划运行时,常规火电装机开机过多,机组利用小时数偏低,新能源弃电严重;如若过分高估光热的容量效益,可能在极端天气时光热发电不足,影响系统供电可靠性。如何在既保证供电可靠性又兼顾风光等可再生能源消纳的前提下,评估光热机组容量效益、计算其参与平衡的容量,给规划运行人员提出了新的挑战。

国外已有文献研究分析光热的容量效益,国内对这方面研究较少。文献[25,26]提出了光热机组与风电联合优化运行,降低风电的不确定性,进而提高系统可靠性。文献[27,28]对比分析了是否含有储热的光热机组在可靠性方面差异,含有储热后,机组容量可信度由原来的60%～86%提升到79%～92%,文献计算的容量可信度较高是由于其使用峰荷负荷率法计算,且算例系统负荷发生在午高峰,并未考虑应对极端天气的情况。此外,文献[29-33]对光热电站建立数学优化模型。

本文在逐次切负荷法基础上,考虑光热历史出力统计特性,并结合光热运行的优化模型,求解光热在最大负荷典型日的工作出力,进而得到光热参与平衡的容量。

2 光热参与电力平衡容量计算思路

光热电站以经济性最优为目标,配置方案中会增加较大容量储热装置。储热装置能够存储热量,并且具有跨日调度热量的能力,可在合适时候释放,使得光热机组具有参加系统电力电量平衡的能力。

光热机组要替代火电装机,就必须在最长连续无光照的日子里仍然能够发电。在这些天里,光热机组只能由储热装置放热发电,最极端情况就是系统的电力平衡控制时刻发生在储热装置日放热量最小的一天内。

对于在特定地区的某一历史年份,光热机组经过优化调整之后,将汽轮机全年日耗费热能的最低值确定为该站在该年的日保证热量。统计多年的日保证热量,可以选择在保证率水平下的数值,并定义为该站的日保证热量。引入储热调节因子概念,此值等于电站的日保证热量除以最大蓄热量。

文中给出的主要思想是,首先根据光热出力特性,可以得出在连续极端气候下,光热机组在典型日中的有效可用热量;然后通过对典型日的模拟,引入上述有效热量,可以算出光热机组的工作出力;从而得到光热机组容量效益。本方法针对各种型式光热如塔式、槽式等都适用,后文将以塔式光热为例加以讲解。其主要过程如图1所示,具体如下:

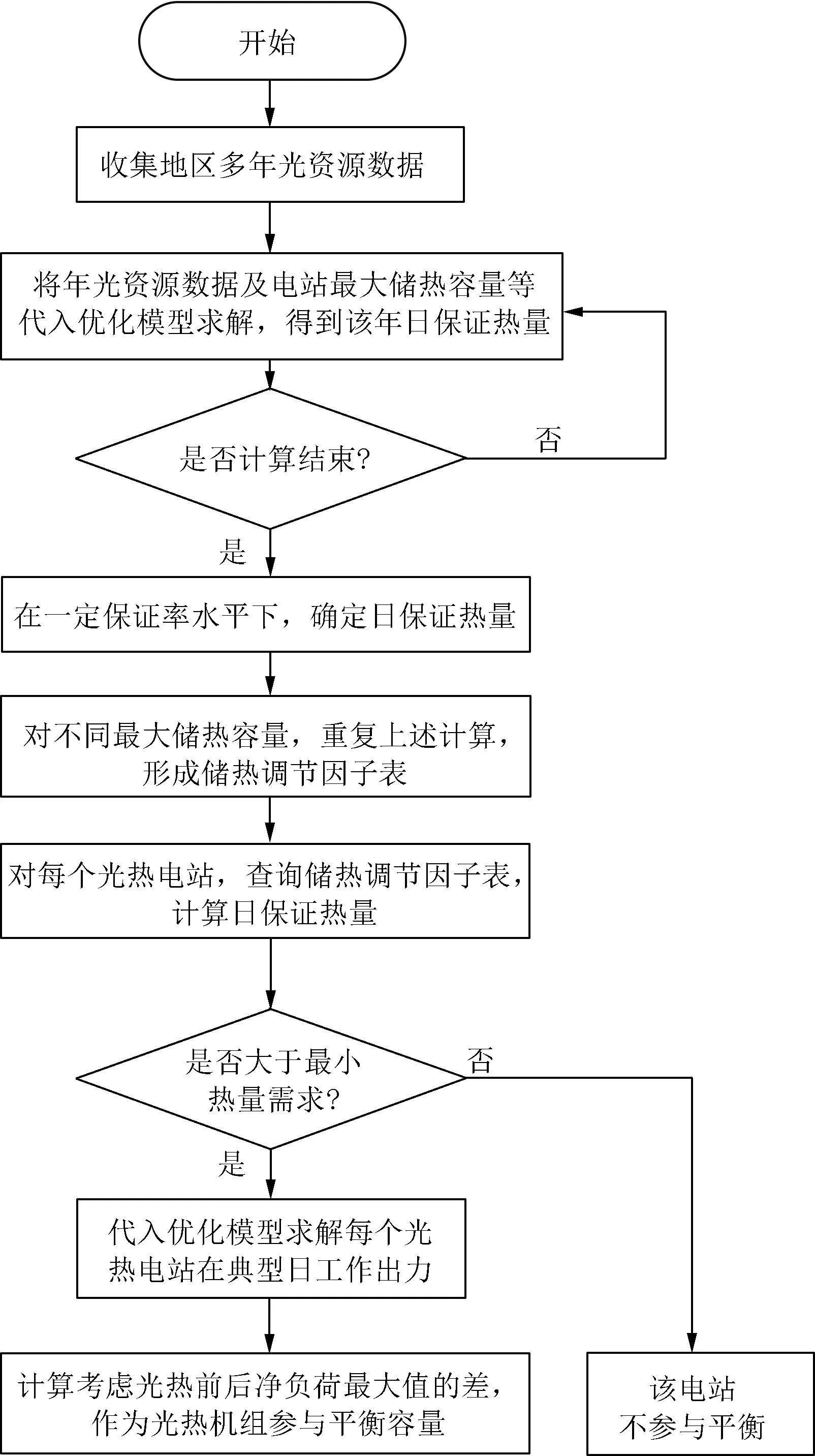
图1 光热电站参与电力平衡容量计算思路图Fig.1 Calculation of participating power balance capacity of solar thermal power station

(1)收集光热电站所在地的多个历史年8 760逐小时光资源数据。

(2)构建线性优化模型(优化模型1),通过考虑指定场所光热电站的光资源数据及机组储热容量等参数,计算得到其对应年份的日保证热量。

(3)将多个历史年份保证容量排序,考虑合适保证率水平,确定日保证热量,对不同储热容量,重复计算作业,得到调节因子表。

(4)对于待分析的光热电站,该电站的日保证热量为储热调节因子与储热装置容量的乘积。

(5)继而代入建立模型(优化模型2+3或2+4),求解光热电站典型日工作出力过程。

(6)最终考虑光热工作出力前后系统净负荷最大值的差即为光热机组参与平衡容量。

需要指出的是,本文重点分析只有光热这一种调节电源时,其对系统充裕度的贡献。当系统中含有水电、抽蓄、储能电源等多种调节电源时,光热的容量效益应与这些调节电源一起考虑,在计算光热工作出力的模型中加入上述调节电源模型即可,本文不展开说明。

3 光热电站日保证热量的确定

3.1 光热电站出力特性

光热电站不考虑系统需求时,典型日运行模拟如图2所示。光热电站配备了储热系统,可以在系统负荷高峰时发电带负荷,减少系统其他机组的开机,具有一定的容量效益。

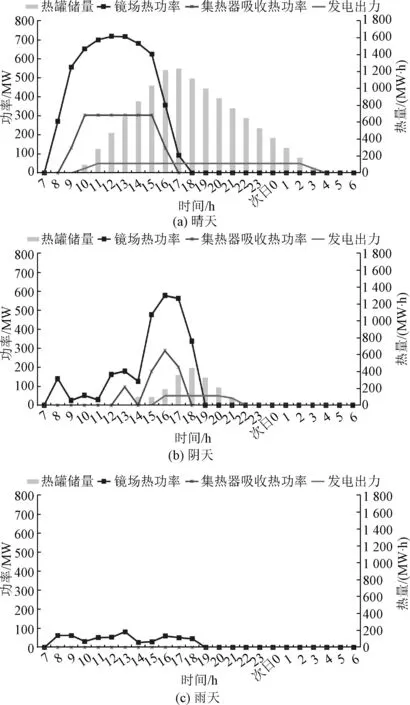
图2 光热电站不参与调峰时典型日运行图Fig.2 Typical daily operation chart when CSP power station does not participate in peak regulation

光热每日可发小时数日间波动较大且具有不确定性,其值可能为0～24 h。此外,也存在连续大发或者连续为0的天。如图3所示,对青海某地在某一年中光热机组运行模拟结果统计,光热机组有50天左右全天不启动。

图3 光热电站某年日出力特性图Fig.3 Characteristic diagram of solar thermal power plant’s daily output in certain year

3.2 光热电站日保证热量优化模型(优化模型1)

为了应对连续多日资源不好的情况,光热电站需要储存部分热量并进行跨日调节热量。光热电站具有这种跨日调节的能力:以塔式熔盐电站为例,其热熔盐储罐中熔盐温度为565 ℃,每天温降可忽略不计。

本文建立了以下线性优化模型,计算光热电站某一时间段内(本文为一年)的日保证热量。光资源具有统计学特征,再根据多年历史光资源数据计算光热电站的日保证热量。

(1)

考虑的约束条件为:

储热装置储热量连续约束,如下式所示:

(2)

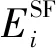
(2)不等式约束。

根据定义,光热电站的日保证热量为机组全年日汽轮机消耗热量的最小值,即满足以下约束:

(3)

储热装置存储的热量上限约束:

0≤Ei≤Emax

(4)

式中,Emax为储热装置存储热量上限。

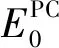
(5)

求解模型可得日保证热量。为了获取该电站的日保证热量,需要对每一历史年份的光照资源情况进行上述计算,从而得到多个年份的日保证热量。然后,在一定的保证率水平下,确定该电站的日保证热量。

山西省临汾市曲沃县的耕地面积约40万亩，当地樱桃种植较为集中，是万亩樱桃种植基地，所以种植户对葡萄的产量和品质要求较高。为了扩大云天化品牌在曲沃市场的知名度，让农民朋友感性认识云天化系列复合肥的优良效果，通过与当地农户交流、探讨，制定了本次试验示范。

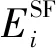
在本研究中,引入了一个新的概念,即储热调节因子α,其通过下述公式来确定:

(6)

对具有不同最大储热量的光热电站进行重复计算,从而得到储热调节因子表。对某一给定的地点,电站日保证热量仅取决于储热装置的最大存储热量。可通过一次计算得到不同储热时长(即储热装置的最大存储热量)的储热调节因子表,日后可通过查表得到保证热量,减少重复计算。

4 光热参与电力平衡的容量研究

4.1 光热电站参与电力平衡模型(优化模型2)

光热电站日保证热量只可供机组发电数小时,不可为系统提供长期备用。光热电站的容量效益体现在其带负荷能力上,不承担系统备用。要确定光热电站的容量效益,先要计算电站的工作出力。

目标函数为考虑光热电站参与平衡后,典型日系统净负荷曲线最大值和累积加和最小,即:

(7)

(8)

(9)

(10)

4.2 单个光热电站优化模型(优化模型3)

单个光热电站的出力模型如下所示:

(1)等式约束

(11)

(12)

储热装置热功率平衡约束为:

(13)

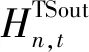
储热装置的吸热平衡方程为:

(14)

(15)

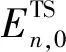
(16)

式中,αn为第n个光热电站储热调节因子。

输入汽轮机的热功率用于启动机组和发电:

(17)

光热电站的热与电转换函数为:

(18)

(2)不等式约束

光热电站发电热功率上限:

(19)

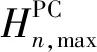
机组启停机时长约束:

(20)

光热电站启动时刻约束:

(21)

光热电站出力大小限制约束:

(22)

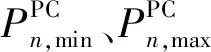
储热装置放热功率约束:

(23)

储热装置存储热量要满足约束:

(24)

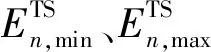
本文通过C++调用Cplex求解上述模型,得到光热电站的工作出力。光热电站参与电力平衡的容量为考虑光热电站出力的最大净负荷差。

4.3 光热电站典型日出力模型的简化(优化模型4)

当光热电站的日保证热量较小,且需电站尽可能多出力时,可作如下假设:每一光热电站在典型日只启停一次;且电站尽可能以高功率工况连续运行,不参与系统调峰,可认为机组电热效率恒定。

(25)

式中,ηn为第n个光热电站的电热效率。

满足以上假定条件的光热电站,可当作发电量给定的水电机组,等效水电机组考虑的模型如下:

典型日可发电量为:

(26)

其发电功率满足约束:

(27)

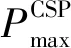
日发电量为:

(28)

求解上述模型,可以计算光热电站的工作出力,进而求解参与平衡容量。

5 算例与分析

对上述优化模型,本文以青海为算例进行计算分析。本文选取单个光热电站为50 MW的机组,储热时长14 h,其他参数见表1及图4。本算例采用青海某地光热电站吸收热量数据。数据样本为2005年～2014年(数据来自美国国家太阳辐射数据库(NSRDB))。

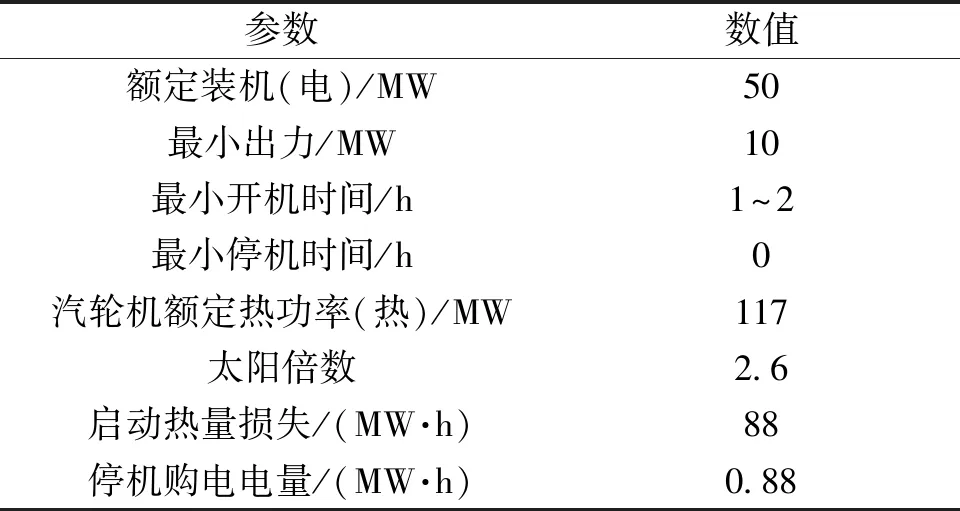
表1 光热机组主要参数Tab.1 Main parameters of CSP

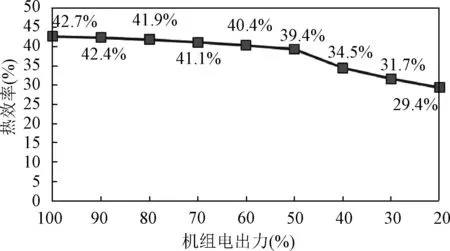
图4 光热机组汽轮机效率曲线图Fig.4 Steam turbine efficiency curve of CSP

5.1 储热时长与储热调节因子

因为信息量大,本例中只附部分数据。连续不利天气对光热电站参与平衡结果影响较大。以2005年为例,该地光照资源数据片段见表2。

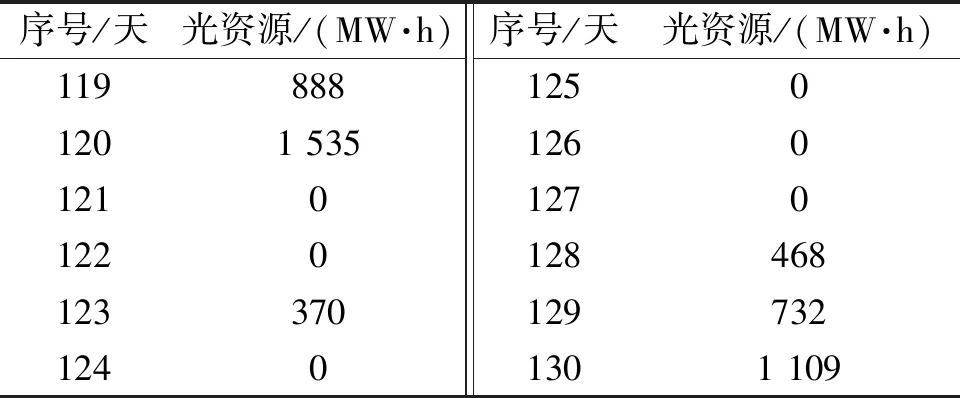
表2 典型年光资源数据(片段)Tab.2 Light resources in typical years (fragments)

将青海典型年天气数据,储热时长为14 h(最大储热量 117×14 MW·h)的光热机组参数代入优化模型计算。求解模型(优化模型1)得日保证热量为287 MW·h,储热调节因子0.175。在第120天结束时储热装置储满热量,需要应对最长连续7天(第121～127天)的不利天气,结果见表3。

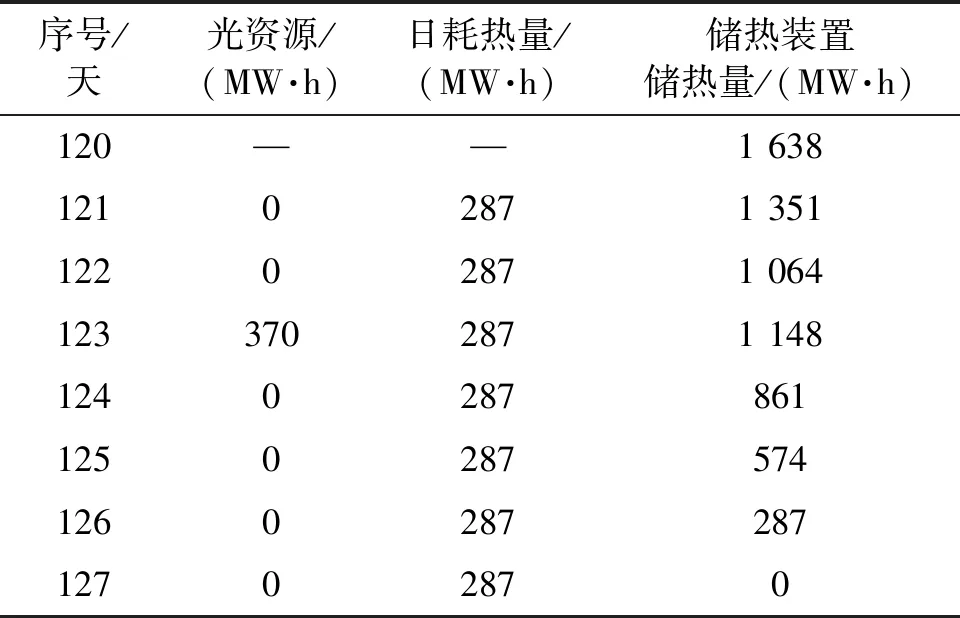
表3 电站应对连续不利天气时运行模拟结果Tab.3 Operation simulation results of power station in response to continuous adverse weather

为了指导光热电站调度运行,本文提出了一种基于优化结果的控制策略。以最长连续的不利天数7天为周期。在每一周期初始时刻,电站储热装置储热量达到最大可能值;光热每日消耗热量在计算周期内根据系统需求协调调度,但电站每日消耗热量不小于日保证热量;在计算周期结束时,储热装置尽量存满热量。

重复上述计算步骤,将得到数据样本中每一年的日保证热量,结果见表4。

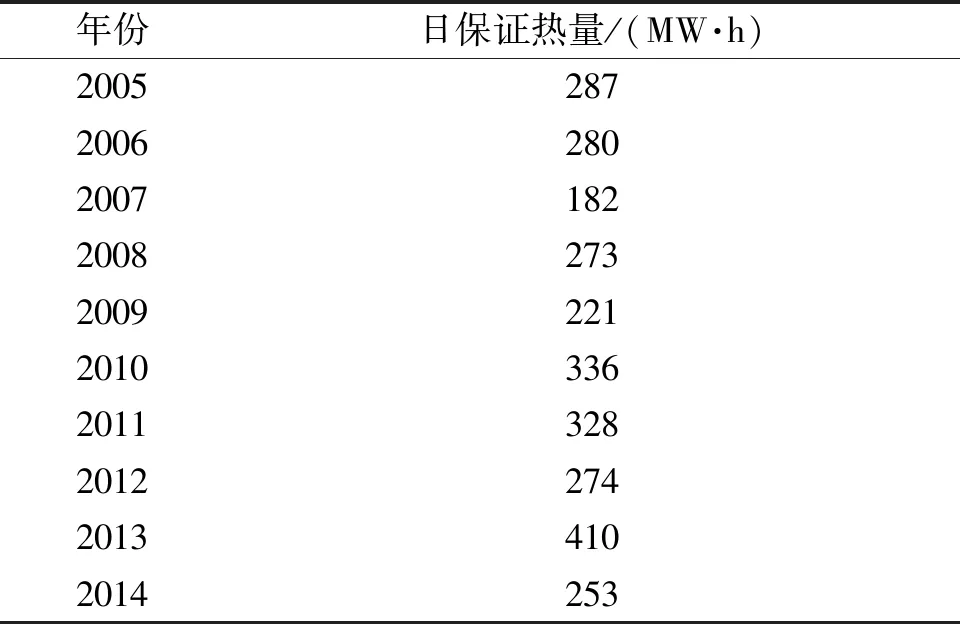
表4 2005～2014年的逐年日保证热量Tab.4 Guaranteed daily heat per year from 2005～2014

在90%的保证率下,光热电站的日保证热量为221 MW·h。

对选定的地区,光资源数据不变。仅改变光热电站的储热时长,代入模型(优化模型1)中计算,储热调节因子随储热时长的变化结果见表5。随着储热时长增长,日保证热量随之增加,储热调节因子随之降低。当储热时长过短时,机组的日保证热量过小,不能满足启动需求,电站容量不可参与电力平衡。

表5 电站储热调节因子表Tab.5 Power station heat storage adjustment factor

5.2 光热电站参与电力平衡容量计算与分析

图5为典型日算例系统的净负荷曲线。青海系统该年最大负荷11 000 MW。假设系统新增加光热装机2 000 MW。查表得到储热调节因子,确定日保证容量。假定系统机组参数统一:装机容量50 MW,储热时长14 h,储热调节因子0.175。

图5 日净负荷曲线图Fig.5 Daily net load curve

求解本文建立的优化模型(优化模型2+3),得到光热机组的工作出力如图6所示。系统共有40个光热电站,每个电站的日保证热量仅可保证机组发电约1.7 h。考虑光热参与平衡后净负荷最大值为10 265 MW,光热容量效益为735 MW,容量可信度为36.75%。若采用简化模型(优化模型2+4),用等效水电机组计算,光热电站总出力过程如图7所示,考虑光热参与平衡后净负荷最大值为10 255 MW,光热容量效益为745 MW,计算结果偏乐观。

图6 光热机组工作出力图Fig.6 Working output diagram of CSP unit

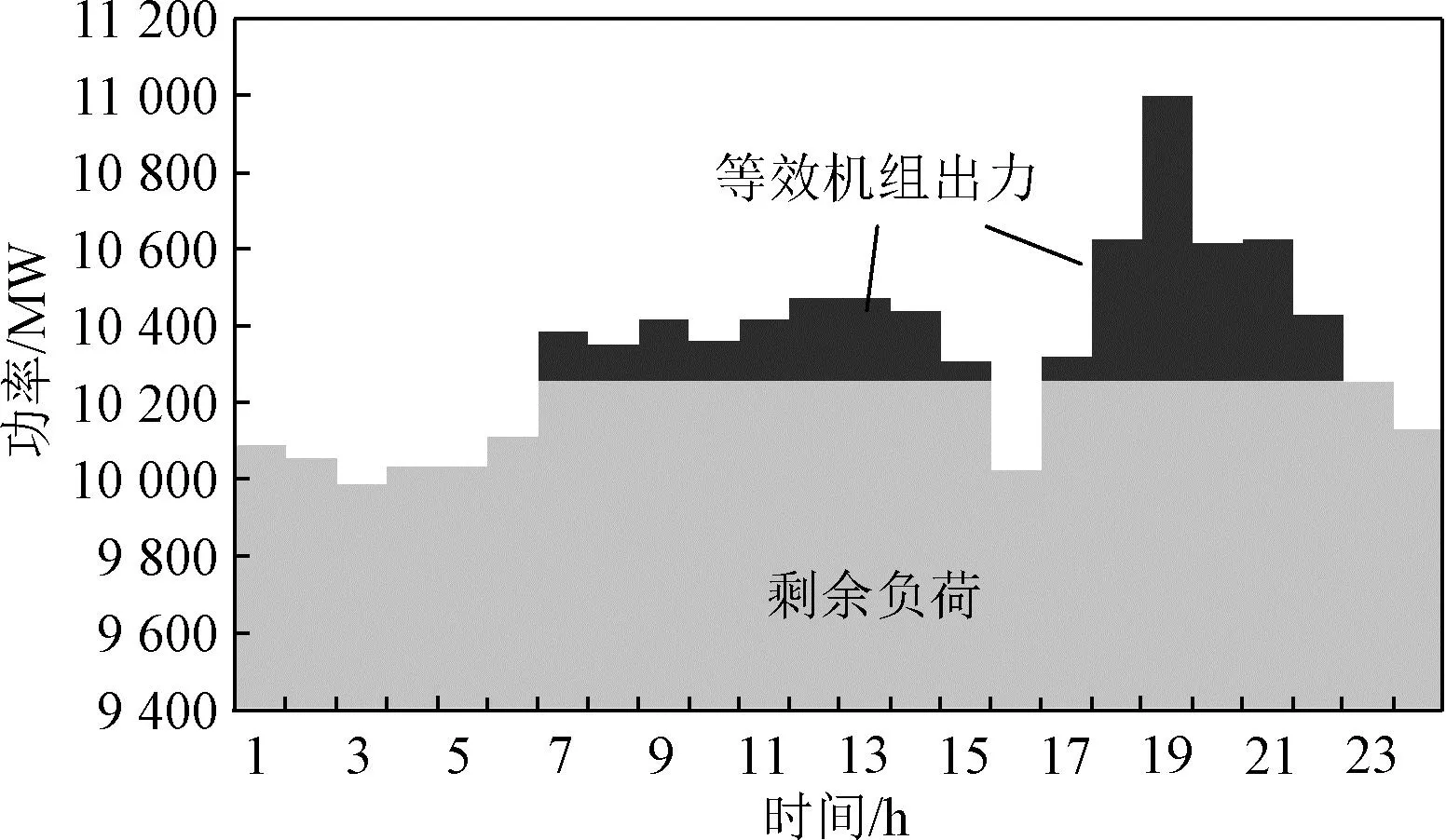
图7 等效机组工作出力图Fig.7 Working output diagram of equivalent unit

为了进一步比较两种方法的差异,改变系统中光热电站的装机规模及日保证热量,计算光热电站参与平衡的容量。当光热机组的装机规模为200～8 000 MW时,计算结果如图8所示。两种方法计算结果接近,等效为水电装机的方法计算结果略乐观一些;同时,随着光热装机规模的增加,其容量可信度由100%降至15%。

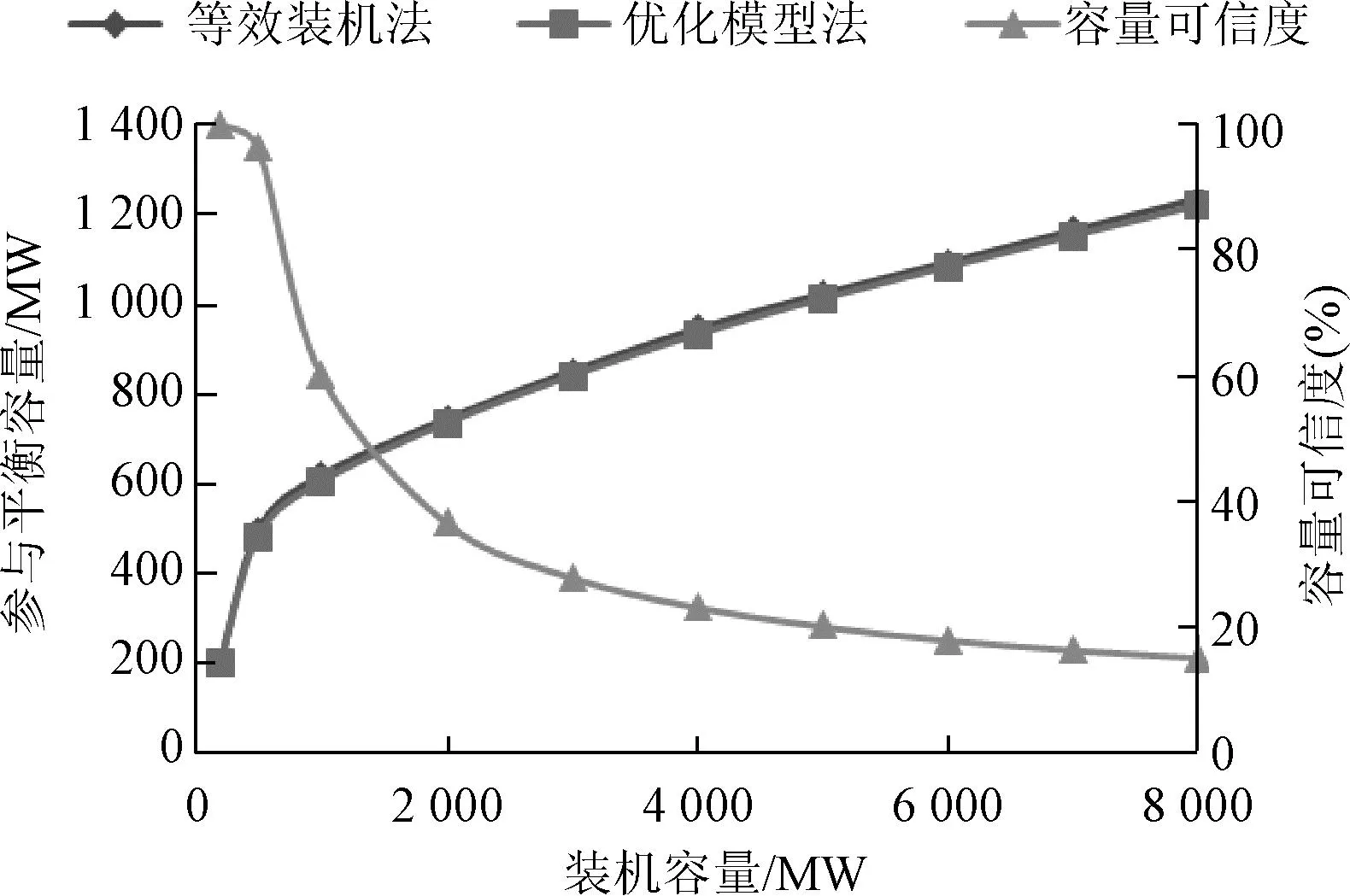
图8 光热机组容量可信度与装机容量关系Fig.8 Relationship between capacity reliability and installed capacity of CSP units

每一光热电站的日保证热量由170～460 MW·h变化时,计算结果如图9所示。两种方法计算结果在日保证热量较少时差异较大,日保证热量较大时接近;等效为水电装机的方法计算结果略乐观一些;同时,随着光热日保证热量的增加,其容量可信度由26%增至46%。

图9 光热机组容量可信度与日保证热量关系Fig.9 Relationship between capacity reliability of CSP units and daily guaranteed heat

经以上分析,在日保证热量较低时,电站无法满出力运行,机组运行效率下降较多,故用等效法算出的结果偏差较大,此时需用优化算法计算;其他结果表明二者计算结果接近,两种方法都适用。

5.3 光热电站调度方式对参与电力平衡容量影响

西北地区光资源丰富,青海、甘肃等地规划建设千万千瓦级光热装机。但光热电站单个电站装机较小,现常见的单机为50 MW。当光热装机规模较大时,机组数量过多,单一电站层面的优化调度较难实现。用5.2节的计算结果参与电力平衡,可能较为乐观,在实际调度中不易实现。

由于地理位置临近的光热电站,其光资源条件也较为接近。本文提出将临近的若干个机组当作一个集群,进行统一调度,随后再进行参与电力平衡的容量计算。

对5.2节算例中的光热电站进行调度集群时,当最小调度容量由50～2 000 MW变化时,计算结果如图10所示。随着集群容量增大,参与平衡的容量随之减少,容量可信度由37%降至26%。

图10 光热机组容量可信度与最小调度容量关系Fig.10 Relationship between capacity reliability of CSP units and minimum dispatch capacity

当最小调度容量为500 MW时,光热机组的工作出力如图11所示。全系统的光热电站,划分为4个集群,各个集群内的每个电站统一启停、统一调节出力,电站的灵活性较差,故参与电力平衡的容量比单独调度时低。

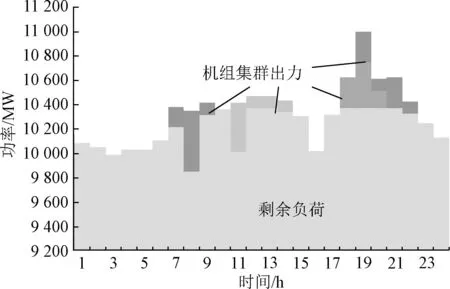
图11 光热机组集群调度时工作出力图Fig.11 Working output diagram of CSP cluster scheduling

6 结论

如何合理评估光热机组参与电力平衡的容量,本文提出了一种基于光热出力特性的计算方法,并对实际算例计算分析。主要结论如下:

(1)以地区典型年光资源条件及电站储热时长等参数为输入变量,建立了一个线性优化模型。通过求解这个模型,得到光热电站的日保证热量。本文引入储热调节系数,便于后续快速确定日保证热量。日保证电量基于多年资源数据,算例中取10年。

(2)以光热参与平衡后净负荷最大值、累积值均最小为目标函数,建立优化模型,并对光热模型简化,同时提出将光热等效为水电机组计算其工作出力,进而得参与平衡容量。

(3)通过算例表明,储热调节因子与储热时长负相关;当储热时长过短时,光热机组不可参加电力平衡;提出满足日保证热量的光热运行策略。

(4)光热机组的容量可信度与光热装机规模负相关,与日保证热量正相关。当装机规模较大时,应采用集群调度,此时只可用优化模型计算。