基于TOPSIS优化永磁同步电机预测控制成本函数

周 立, 薛孟娅, 金烜旭, 李京明, 尚治博, 刘金澍

(1.辽宁工程技术大学电气与控制工程学院, 辽宁 葫芦岛 125105;2.辽宁理工职业大学机电学院, 辽宁 锦州 121000;3.中南大学交通运输工程学院, 湖南 长沙 410075; 4.国网河南省电力公司商丘供电公司, 河南 商丘 476000)

1 引言

永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)因高功率密度、高性能、低能耗和强大的动态特性以及对环境的适应性等优点,被广泛地应用于中低功率高性能电动驱动器,如计算机外围设备、机器人、可调速驱动器和电动汽车[1,2]。

模型预测控制(Model Predictive Control,MPC)可将多个目标集成到单个成本函数(Cost Function,CF)中。由于其多变量控制适应能力强、计算效率高、复杂度低、非线性插入和局限性,它在PMSM研究中得到了广泛应用[3-5]。MPC的工业用途包括牵引传动[6]、电力船舶推进[7]、风力发电机[8]等。文献[9-11]将预测控制与直接转矩控制(Direct Torque Control,DTC)相结合,结果显示预测值与实验结果基本保持一致。连续控制集预测控制中的调制步骤可以用来获得固定的开关频率,但预测过程很困难。有限控制集预测控制在不使用外部调制步骤的情况下可优化开关状态[12]。

文献[13,14]中提出基于周期控制方法和扩展周期控制方法来获得有限控制集预测控制的固定开关频率。但是,连续控制集预测控制和有限控制集预测控制在权重因子(Weight Factor,WF)调整方面都具有显著的计算负担和成本函数优化问题,尤其是在多电平逆变器方面。由于成本函数的权重因子对PMSM驱动控制性能指标有直接影响,如开关频率和谐波失真率(Total Harmonic Distortion,THD)。因此,有必要调整MPC的成本函数权重因子以提高MPC的控制效果。如果采用试错方法来评估各种权重因子下的MPC性能,则优化过程确实会很耗时[15]。因此,文献[16-20]提出了几种解决这一问题的方法。离线优化方法主要旨在通过分割成本函数维度简化权重因子的难度。文献[18]中PMSM通过加权和方法实现成本函数优化,但该方法存在额外的计算负担。文献[19]消除了权重因子,以快速实现基于多电平逆变器的MPC的开关状态。文献[20]中通过合并可控的目标参数,采用无权重系数模型预测控制方法,但这种方法只适用于彼此密切相关的可控目标参数。权重因子对系统性能有显著影响,因为它分布了每个调节状态的值。这些参数是根据经验确定的[21]。文献[22]通过转矩和磁通变化以及定子电流的整体谐波失真用于确定最佳的权重因子。但是,使用转矩脉动误差最小方法选择权重因子,导致设备的成本会上升。通常,离线优化方法主要用于降低成本函数的难度,以使调整权重因子更容易,但这种方法不能用于彼此独立的权重因子。

在线优化方法通过改进观测器来跟踪和调整成本函数的权重因子。文献[16]中提出了一种动态计量优化切换矢量的在线优化方法,通过创建电压观测器以在减少转矩纹波的基础上优化权重因子。文献[17]使用双层变压器减少有限控制集预测控制转矩脉动的在线优化方法,将控制周期分为两部分:施加有源电压和零电压的有源周期和零周期。在该方法中以动态方式更新成本函数。通过预测要控制的目标误差轨迹优化权重因子。总之,在线优化方法经常使用类似观测器的方法来动态调整权重因子,与离线优化方法相比,在线优化方法增加了MPC的计算工作量。

综上,本文提出了一种多目标决策分析方法,即逼近理想解排序法(Technique for Order Preference by Similarity to an Ideal Solution, TOPSIS)[23],每个对象有多个属性,优化的目标是找到一个控制序列。为了实现TOPSIS,将逆变器的7个现有电压矢量作为预测控制中基于TOPSIS成本函数优化的控制序列,将电磁转矩和定子磁链纹波视为选择理想解的标准。为了降低本文所提控制方法的总体计算复杂性,根据先前的最佳状态来选择预定义的切换时刻。

2 永磁同步电机离散电流模型

实现预测控制方法需要对永磁同步电机进行离散建模。欧拉离散化方法可以对以导数形式表示的变量进行离散,例如在状态空间模型的情况下的状态矢量。以下是连续时间内的PMSM在旋转参考系下的建模方程:

PMSM的定子电压方程为:

ud=Rsid-ωrψq+ρψd

(1)

uq=Rsiq+ωrψd+ρψq

(2)

式中,ud、uq、ψd、ψq、id、iq分别为d、q轴上的电压、磁链和电流分量;Rs、ωr分别为定子电阻、转子机械速度;ρ为差分运算符。

定子磁链方程为:

(3)

式中,Ld、Lq分别为电感在d、q轴上的分量;ψf为转子磁链。

PMSM的电流方程为:

(4)

(5)

PMSM的电磁转矩方程为:

(6)

式中,Pn为极对数。

式(4)和式(5)生成了永磁同步电机的离散建模,代入欧拉公式得电流的导数为:

(7)

式中,Ts为采样时间;ik为当前状态值;ik+1为下一时刻的状态值。式(7)修改为当前状态和下一时刻的状态关系:

(8)

PMSM的离散电流方程为:

(9)

(10)

电流状态空间方程为:

(11)

3 基于TOPSIS的PMSM预测控制

3.1 TOPSIS方法及实现步骤

TOPSIS是一种对多目标问题进行优劣排序的基本方法,该方法首先由C.L.HWANG等人提出,它主要通过计算评价对象与理想解的接近程度来综合排名,以获取最优解。

假设TOPSIS标准值的增加或减少对结果的影响方向是一致的。在多目标问题中,归一化通常是必不可少的,因为参数的维数往往不一致。传统上只有一个成本函数,但为了实现TOPSIS方法,将单个成本函数分为两个成本函数,一个与转矩有关,用GT表示,另一个与磁通有关,用Gψ表示,如下:

(12)

(13)

TOPSIS的分析步骤如下所示:

(1)有m个可变电压和n个标准(Te和ψs),每个备选方案和标准的交集为yij,得矩阵(yij)m×n为:

(14)

(2)矩阵(yij)m×n标准化,得出归一化矩阵R为:

R=(rij)m×n

(15)

通过使用归一化方法,得:

(3)加权归一化判断矩阵为:

(16)

(4)根据归一化值,转矩和磁链的正理想切换状态和负理想切换状态程为:

(17)

(18)

(19)

(20)

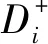
(21)

(22)

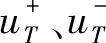
(6)计算相对接近度系数Ci如式(23)所示,以获得每个开关状态相对于正理想解的相对接近度。

(23)

(7)根据接近度系数值对切换状态从大到小进行排序,贴近度最大者为最优方案。

对于选定电磁转矩和定子磁链的误差,将逆变器的7个现有电压矢量作为预测控制的7种控制序列,考虑到系统性能稳定性,Ci最大值最优。基于TOPSIS预测控制的最佳可能切换状态用粗体表示见表1,当开关处于S1时,第i次转矩参考值与转矩预测值的差绝对值为0.31,第i次磁链参考值与磁链预测值的差绝对值为0.012,第i次正理想切换瞬间的欧氏距离为0.137 2,第i次负理想切换瞬间的欧氏距离为0.598 2,第i次相对接近度系数为0.813 5。

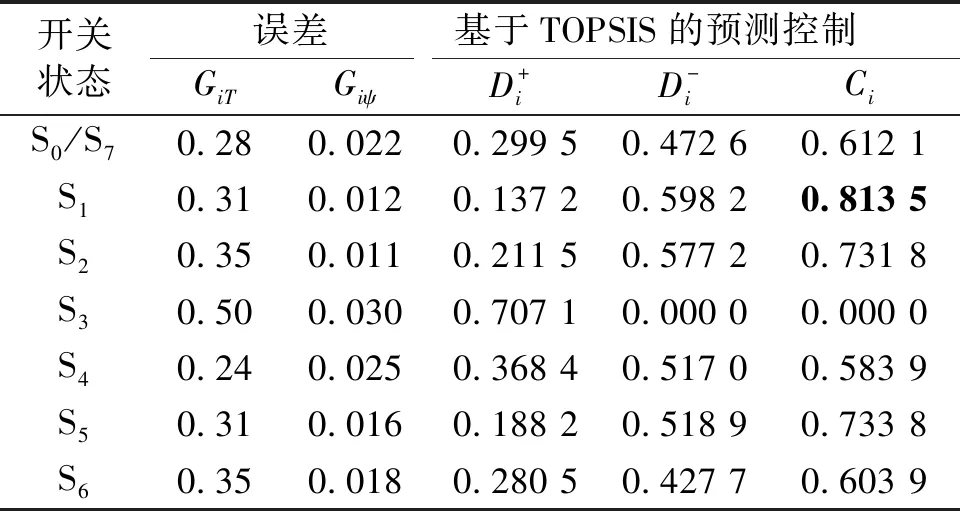
表1 基于TOPSIS预测控制的开关状态选择Tab.1 Switching state selection for predictive control based on TOPSIS method

3.2 基于TOPSIS的PMSM预测控制优化设计

图1 永磁同步电机控制框图Fig.1 Control block diagram of permanent magnet synchronous motor

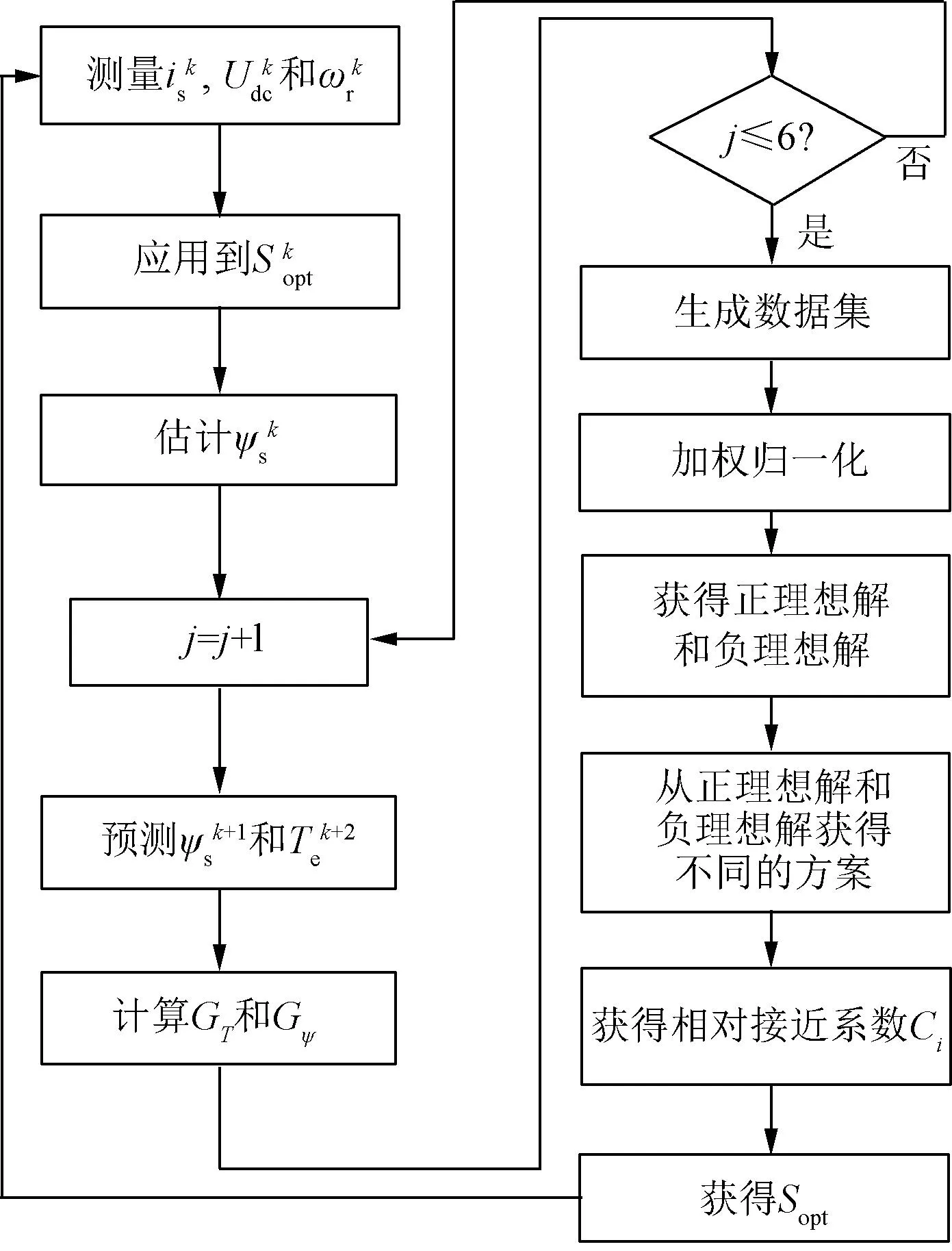
图2 TOPSIS成本函数优化方法流程图Fig.2 Flow chart of TOPSIS cost function optimization method

4 仿真结果与分析

为了验证基于TOPSIS预测控制的有效性,搭建Matlab/Simulink仿真平台进行验证,对所提控制方法和传统控制方法进行对比分析。系统中主要参数见表2。

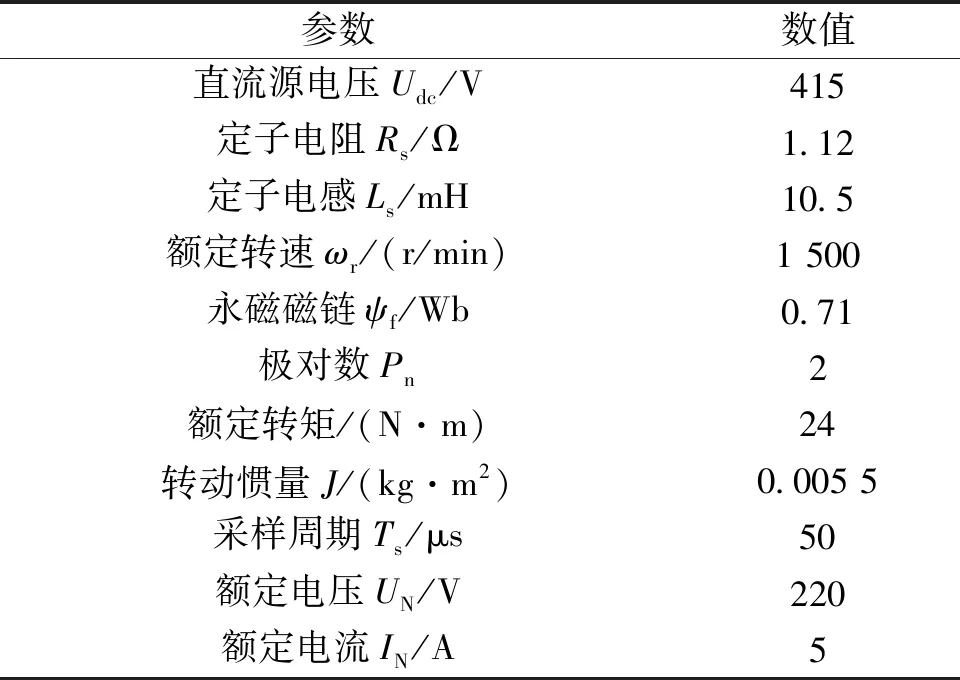
表2 系统仿真参数Tab.2 System simulation parameters

4.1 稳态性能

在电机转速为150 rad/s,负载为12 N·m的工况下。图3和图4分别为在直接转矩控制、预测控制和基于TOPSIS控制下的三相定子电流和电磁转矩脉动波形。

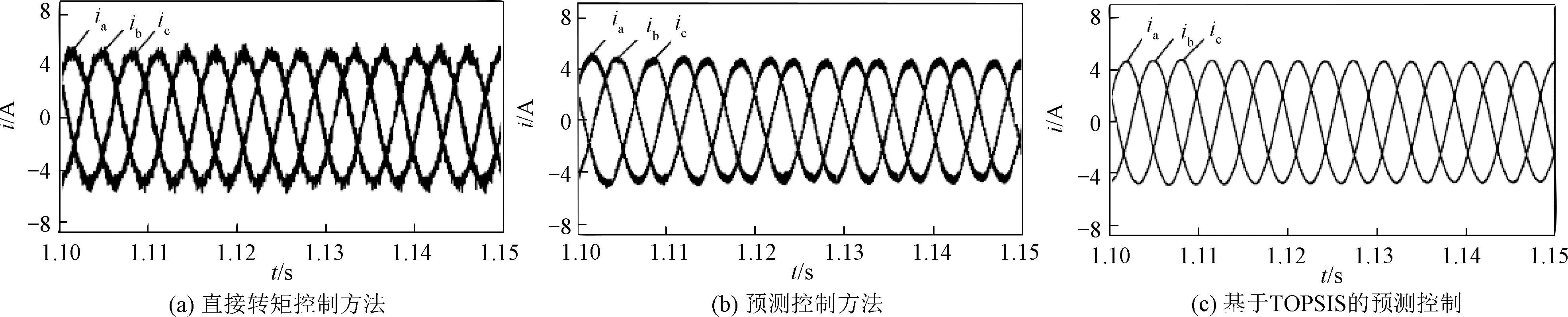
图3 三种控制方法下的定子电流波形Fig.3 Stator current waveforms under three control methods

图4 稳态下三种控制方法的转矩波形Fig.4 Torque waveforms under three control methods in steady state

图4(a)～图4(c)中,三相定子电流总谐波失真分别为7.13%、6.58%、3.41%。电磁转矩的纹波分别为8.35%、5.83%、2.51%。相比较于直接转矩控制和预测控制,可以看出基于TOPSIS方法有更好的电流质量和更小的转矩脉动。

4.2 动态性能

为了进一步验证PMSM改进型模型预测控制动态响应性能,给定初始负载为12 N·m,电机在0.2 s时给电机减载到6 N·m,稳定运行至0.35 s时给电机加载到8 N·m,电机在三种控制方法下的转矩波形和a相电流波形如图5和图6所示。

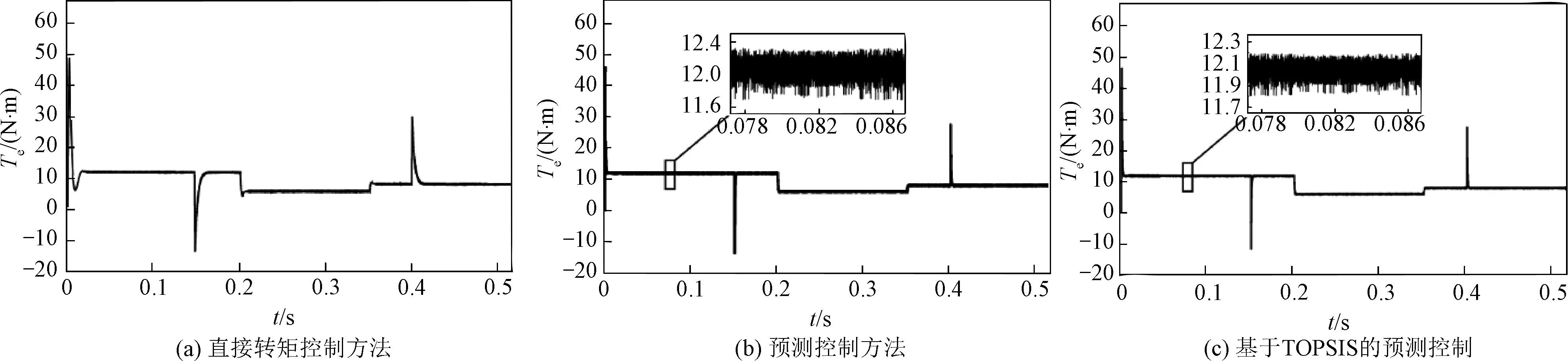
图5 动态下三种控制方法的转矩波形Fig.5 Torque waveform under three control methods in dynamic state

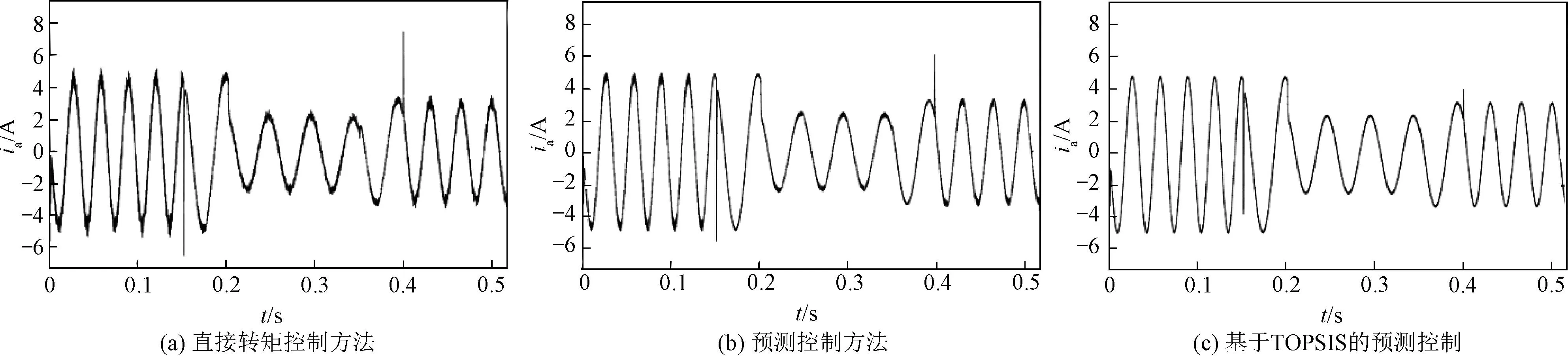
图6 三种控制方法下的a相电流波形Fig.6 Waveform of phase a current under three control methods

从转矩和a相电流的输出波形可以观察到,在加、减速时,电机转矩都分别略有降低和升高,但均能快速回到给定值。然而,对比电流纹波可见,基于TOPSIS的方法有较好的控制效果,进一步验证了本文所提控制策略的有效性。

5 实验结果与分析

在理论和仿真验证的基础上,构建PMSM控制实验平台,如图7所示。

图7 实验平台Fig.7 Experimental platform

控制系统的主处理器基于TMS320F28335的数字信号处理器。与传统方法相比,MPC类方法通常需要更复杂的计算和较大的存储空间,以实现对系统模型的预测和优化,所以控制周期有一定的延长。DSP控制器为电机驱动模块提供栅极脉冲,由电压源逆变器供电,实验中电机参数见表2。对永磁同步电机三种控制方法下的稳态和动态运行特性进行了对比分析。

5.1 稳态运行

在40 rad/s的速度和12 N·m的负载条件下。图8为PMSM在直接转矩控制、预测控制和基于TOPSIS方法的预测控制下的a相电流、电磁转矩、转速和定子磁链实验波形。

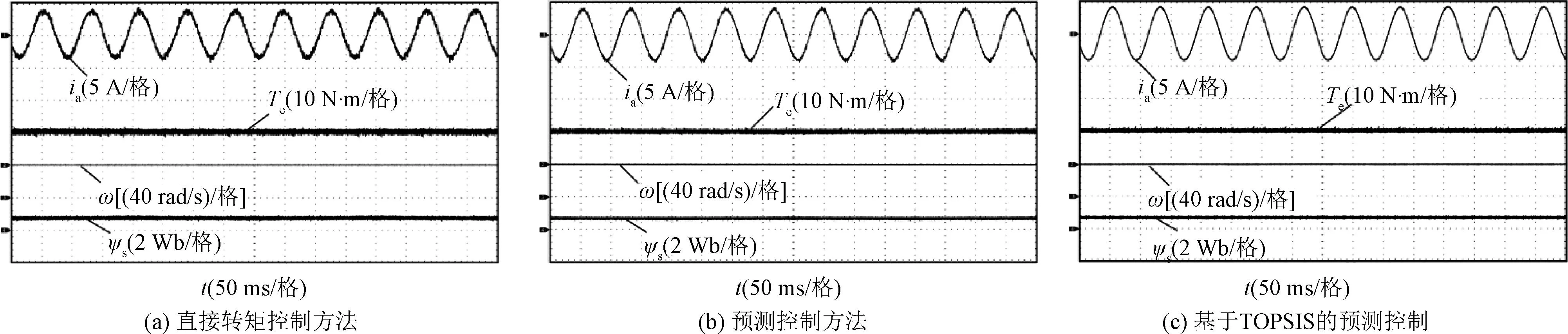
图8 PMSM稳态实验波形Fig.8 PMSM steady-state experimental waveform

图8(a)～图8(c)中,ia的总谐波失真分别为7.91%、6.43%和3.43%。Te的纹波分别为10.31%、8.38%和5.97%。ψs的纹波分别为18.82%、18.64%和18.41%。可以观察到,基于TOPSIS方法控制下减小了Te和ia的总谐波失真。与预测控制相比,基于TOPSIS的方法减小了ψs的纹波。

5.2 动态运行

图9为永磁同步电机的速度正反转下的动态性能。电机从+150 rad/s至-150 rad/s时的动态响应。可以观察到,三种控制方法均有近似的动态响应性能。与直接转矩控制、预测控制相比,TOPSIS方法转矩脉动明显减小,使电机控制系统具有更好的动态性能。

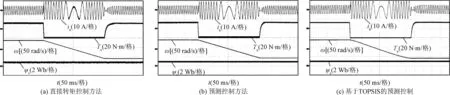
图9 动态响应实验波形Fig.9 Dynamic response experimental waveform

为了更直观对比三种控制策略的系统动态性能,降低模型计算量和减少计算时间问题,相同工况下对比三种控制策略的参考转速跟踪性能轨迹如图10所示,可以看出本文所提控制算法相比DTC和模型预测转矩控制(Model Predictive Torque Control, MPTC)转速在开始阶段超调量更小,系统动态响应时间相比于传统MPTC较快,相比于DTC控制较慢,但很快就能稳定跟踪参考转速。

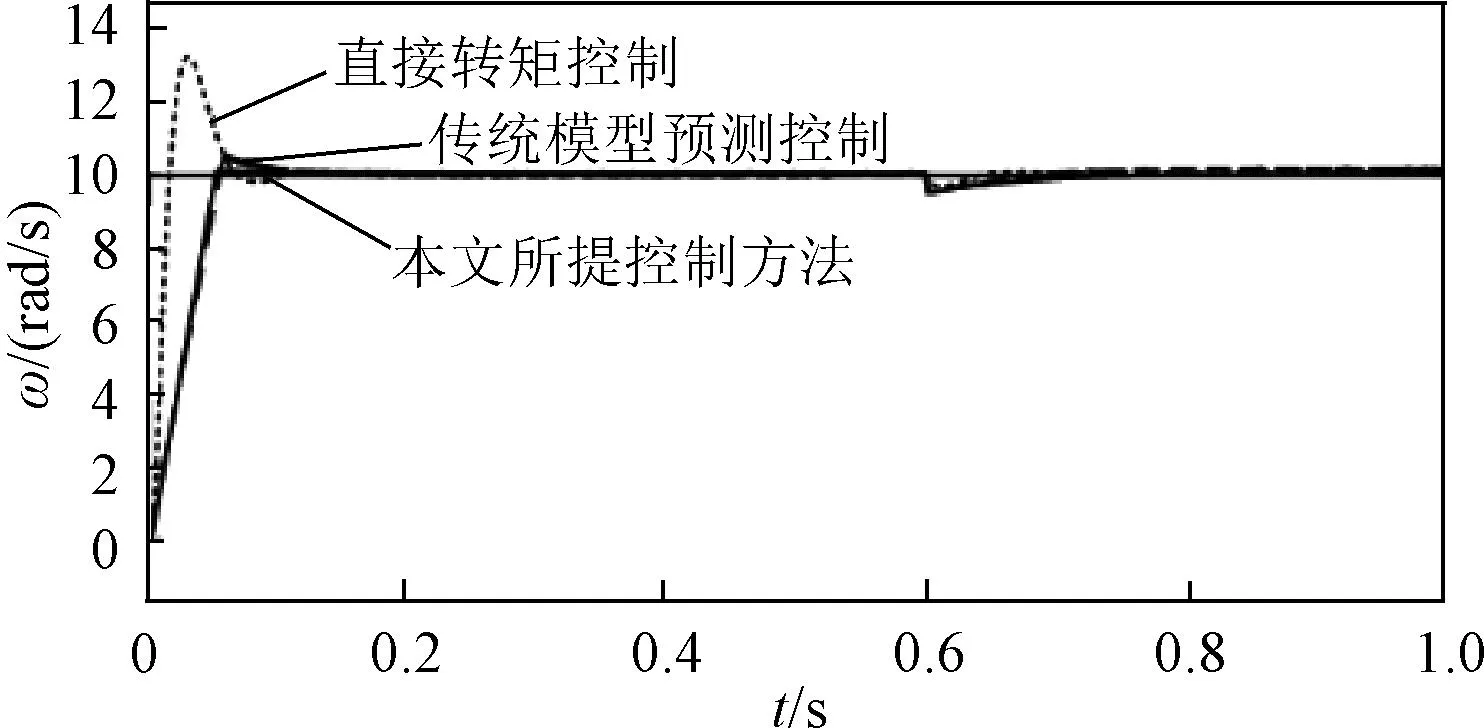
图10 三种控制策略的转速跟踪性能Fig.10 Speed tracking performance of three control strategies

图11为永磁同步电机在直接转矩控制、预测控制和基于TOPSIS方法不同速度下的平均开关频率。可以清楚地观察到,基于TOPSIS方法在电机的各种运行速度下给出了较低的平均开关频率。

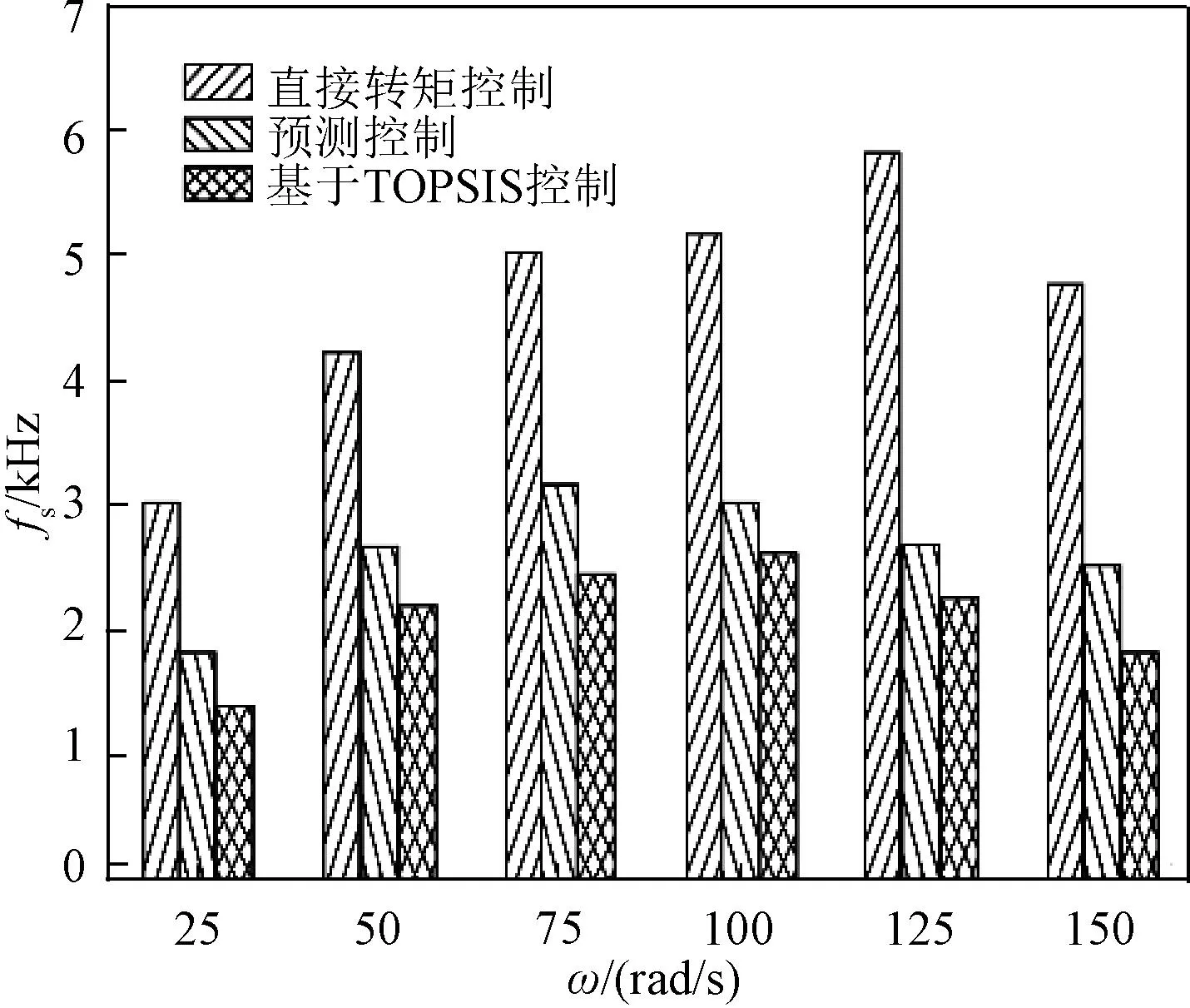
图11 PMSM不同速度下的平均开关频率Fig.11 Average switching frequency of PMSM at different speeds

在转速150 rad/s和12 N·m负载工况下,图12为两级电压源逆变器每相电压及其相应的总谐波失真。可以观察到,直接转矩控制、预测控制、TOPSIS方法的THD分别为32.1%、26.86%和22.14%。与直接转矩控制相比,基于TOPSIS方法的THD减少了31.03%,与预测控制方法相比THD减少了17.57%。

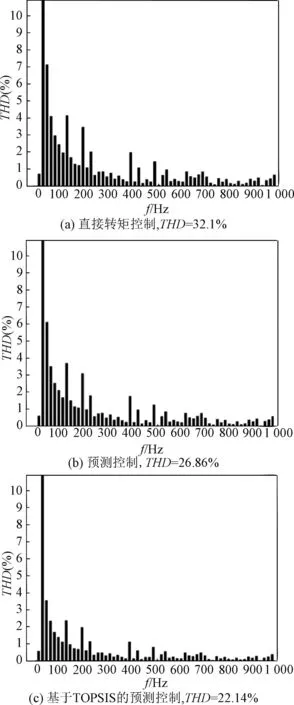
图12 每相VSI电压总谐波失真Fig.12 Total harmonic distortion of VSI voltage per phase

算法的执行时间是衡量控制策略复杂度的重要指标之一,通过DSP控制系统处理的时间作为所提控制策略与传统预测控制的计算复杂度的度量。传统预测控制策略的执行时间为35.2 μs,所提控制策略的执行时间为24.4 μs。所提策略与传统预测控制策略执行时间相比显著减少,DSP处理算法的时间更短,提高了控制系统的实用性。

6 结论

本文对永磁同步电机的控制策略进行研究,针对成本函数中选择适当的权重因子问题,提出了一种基于TOPSIS的永磁同步电机预测控制成本函数优化方法。根据系统需要,可以很容易地控制参数的比例,使用下一时刻的切换瞬间进行预测和CF优化,以减少实现TOPSIS方法的计算量。结果表明,所提控制方法在电磁转矩、定子电流计算量方面均优于传统控制方法,在稳态和动态状态下均表现出优异的性能特性。此外,所提控制策略在CF中可以作为一个可行解决方案应用于各种预测控制方法中。