小型混凝土铣刨机铣刨过程仿真
王寒煜
(广东博智林机器人有限公司,广东 佛山 528000)
0 引言
大型路面铣刨机是成熟的市政工程专用设备,一般适用于大面积的施工作业,但对于小面积的施工作业则不太适用,而小型混凝土铣刨机小巧灵活,能适应各种小面积的施工作业,主要应用于桥面凿毛、旧路面刨除、受损地面修复、室内地面灰浆清理、地面拉毛、住宅等场地的铣刨施工。铣刨施工是一种通过刀片切除表面材料来实现所需表面质量的施工方法,铣刨过程是一个非常复杂的过程,涉及地面与刀具之间的摩擦状态、地面材料的变形、断裂失效等,利用传统的解析研究方法,很难对铣刨过程进行定量分析[1],因此需要采用有限元数值模拟的方法对铣刨过程进行研究。目前业界对大型路面铣刨机的铣刨过程研究较多[2-4],而对小型混凝土铣刨机的铣刨过程研究较少,本文应用ABAQUS 有限元分析软件对小型混凝土铣刨机刀片铣刨水泥混凝土过程进行了有限元数值模拟,铣刨刀片对地面冲击力大小直接反映切削的难易程度,直接影响到设备的可靠性、效率、作业质量及刀片的寿命,是切削过程中最重要的参数之一,本文分析了不同的铣刨深度、铣刨速度、进给速度对冲击力的影响规律,为铣刨工艺研究提供了理论参考。
1 铣刨工作原理
小型混凝土铣刨机整体向前运动的同时,通过电动机驱动铣刨鼓高速旋转,由于硬质钨钢合金刀片内孔与刀轴存在间隙,铣刨鼓高速旋转时,铣鼓刀轴上的合金刀片被甩动并高速敲击地面,利用合金刀片上的刀齿来冲击与磨削水泥混凝土地面,从而实现水泥混凝土表面质量的预期效果,同时铣刨罩壳将整个铣刨鼓包围起来,可以起到抑制铣刨过程中扬尘的作用。
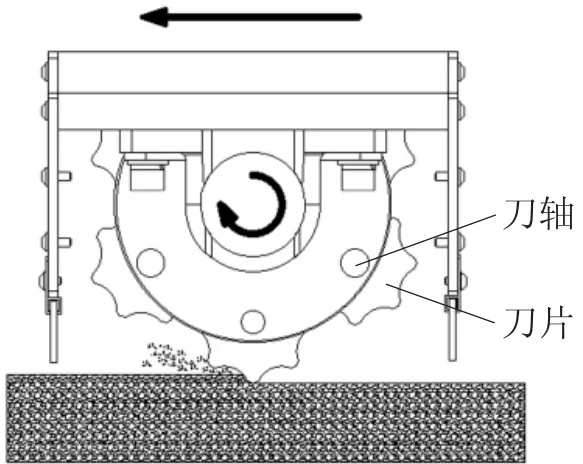
图1 铣刨工作原理
2 建模
2.1 几何模型及网格划分

图2 几何模型及网格
水泥混凝土路面长度为500 mm,宽度为100 mm;铣刨鼓外径为315 mm,刀片外径为150 mm,刀片孔与刀轴间隙为8 mm,由于刀片上的刀齿是均匀对称分布的,因此只模拟一片刀片的铣刨过程。刀片及刀轴被定义为刚体。水泥混凝土单元形状选择为Hex 六面体单元,采用扫掠方式对网格进行划分,扫掠路径为自下而上,选择Advancing Font 进阶算法,选择C3D8R8节点六面体线性减缩积分单元,同时引入了沙漏控制,水泥混凝土单元数为259 200。
2.2 Johnson-Cook模型
本文利用有限元分析软件ABAQUS 中的Johnson-Cook 材料本构模型和Shear Failure 失效准则建立水泥混凝土的有限元模型,水泥混凝土的有限元节点损伤失效判断的依据是该节点是否达到设计参数。Johnson-Cook 本构模型是针对混凝土材料提出的一种损伤本构模型,用来模拟计算混凝土高应变率下的大变形问题[5],能较好地描述混凝土在高速撞击与侵彻下的力学行为,此模型在相关领域中得到了广泛应用[6]。
等效应力方程为
σ=[A(1-D)+Bεn](1+Cln εs*)(1-T*m)。
式中:A、B、n、C、m 为模型参数;σ 为等效应力;ε 为等效塑性应变;εs*=ε/ε0为无量纲化应变率,ε0为参考应变率;T*=(T-Tr)/(Tm-Tr)为无量纲化温度,其中Tr为参考温度,Tm为材料的熔点温度,T 为试验温度。
损伤演化方程为:
εf=[D1+D2exp(D3σ0)](1+D4ln ε*)(1+D5T*)。
式中:D1~D5为模型参数;εf为有效断裂应变;△ε 为等效塑性应变增量;σ0=σH/σ 为应力三轴度,σH为平均应力;损伤参数D 为一个积累量,当损伤参数D达到1时,判断为损伤失效。
相关学者已经通过试验获得了水泥混凝土Johnson-Cook 本构模型参数[7-9],本文基于相关学者的试验成果,选取了一组比较合适的参数,如表1所示。

表1 水泥混凝土Johnson-Cook本构模型参数
2.3 定义接触
本文铣刨数值模拟过程中需要定义3 对接触:第1 对是刀片内孔与刀轴的接触,铣刨鼓旋转过程中,刀片将在离心力的作用下接触刀轴外表面;第2对是刀齿与混凝土的接触,铣鼓高速旋转时,铣鼓刀轴上的合金刀片被甩动并高速敲击地面;第3 对是混凝土的自接触,混凝土破碎后,混凝土碎屑之间、碎屑与未铣刨混凝土之间相互接触。
2.4 边界条件
约束刀轴中心的4 个自由度(U2=U3=UR1=UR2=0),刀轴中心只保留旋转及进给方向运动的自由度;约束混凝土路面的6 个自由度(U1=U2=U3=UR1=UR2=U3=0);约束刀片4 个自由度(U3=UR1=UR2=0),刀片中心只保留旋转及进给方向运动的自由度;刀轴中心与刀轴绑定。
3 铣刨路面模拟结果及分析
刀轴中心与刀轴采用刚体绑定约束并赋予参考点,对刀轴中心参考点施加铣刨深度、铣刨转速和进给速度,铣刨转速为1500 r/min,铣刨深度为1 mm(刀齿最低点侵入地面深度),进给速度为50 mm/s。数值模拟过程中,在刀尖与混凝土接触瞬间,网格变形剧烈,为了防止网格畸变导致的计算困难,铣刨层定义的最小网格尺寸为1 mm,删除完全损伤失效的网格单元。
根据实际作业工况,刀片铣刨水泥混凝土是一个冲击破碎和磨削过程,在刀片接触混凝土的瞬间,冲击力将会急剧上升,随着刀片的旋转,水泥混凝土的弹塑性变形、开裂失效、冲击力会出现一定范围的波动,直到刀片完全脱离地面后完成一次铣刨。由图3、图4 可知:冲击位置出现了剪切破坏,第9 μs 时刀片开始有冲击力;第126 μs 时冲击力达到最大值106 N,此刻铣刨深度也达到最大值,冲击力出现一定范围的波动,随着冲击过程的持续,冲击力不断减小,第504 μs 时冲击力降为0 N,整个铣刨过程持续495 μs。由此可见,有限元计算得出的冲击力变化规律与实际变化规律基本相符。
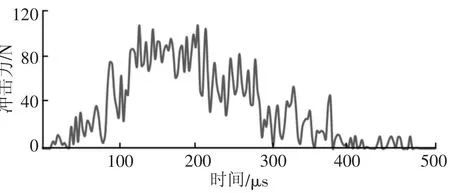
图3 冲击力变化曲线

图4 水泥混凝土应力云图(第126 μs 时)
3.1 铣刨深度对冲击力的影响
铣刨机刀片和刀轴之间存在8 mm 间隙,铣刨鼓高速旋转时,铣鼓刀轴上的合金刀片被甩动并高速冲击地面,取铣刨深度为1~8 mm,铣刨深度为9 mm,铣刨水泥混凝土地面,取铣刨转速为1500 r/min,进给速度为50 mm/s,分析不同的铣刨深度对冲击力的影响。
图5 为铣刨深度不同时冲击力峰值的对比。总体的趋势为:冲击力随着铣刨深度的增大而不断升高,其中铣刨深度在8 mm 以内时,铣刨深度每增加1 mm,冲击力增长5%~25%,铣刨深度为8 mm 时,冲击力为197.3 N,比铣刨深度为1 mm 时的冲击力增长85%;当铣刨深度超过9 mm 时,冲击力急剧增加,冲击力为1051 N,铣刨深度每增加1 mm,冲击力增长4 倍以上。原因是:铣刨深度在8 mm 以内时,在刀齿冲击地面的瞬间,刀片会立即反弹起来,冲击力不再增加;当铣刨深度超过8 mm 时,刀片冲击地面时,刀轴和刀片内孔接触,刀轴阻止刀片反弹,从而迫使刀片继续铣刨地面,造成冲击力急剧上升。因此,在实际施工过程中,需要控制铣刨深度,铣刨深度不能大于刀轴间隙,以防因冲击力过大而造成机器故障。
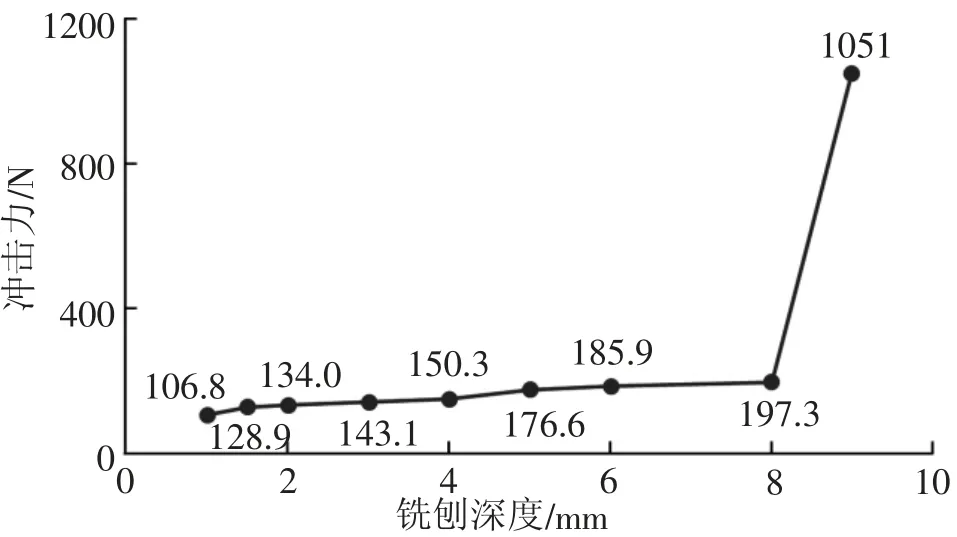
图5 不同铣刨深度对冲击力的影响
3.2 铣刨转速对冲击力的影响
铣刨水泥混凝土路面时,取铣刨深度为1 mm,进给速度为50 mm/s,铣刨转速为1500~2000 r/min,分析不同的铣刨转速对冲击力的影响。
图6 为铣刨转速不同时冲击力峰值的对比。总体的趋势为:冲击力随着铣刨转速的增加而增加,铣刨转速为2000 r/min 时,冲击力为182.4 N,相比于铣刨转速为1500 r/min 时的冲击力增长70%;铣刨转速每增加100 r/min,冲击力增长10%~18%。
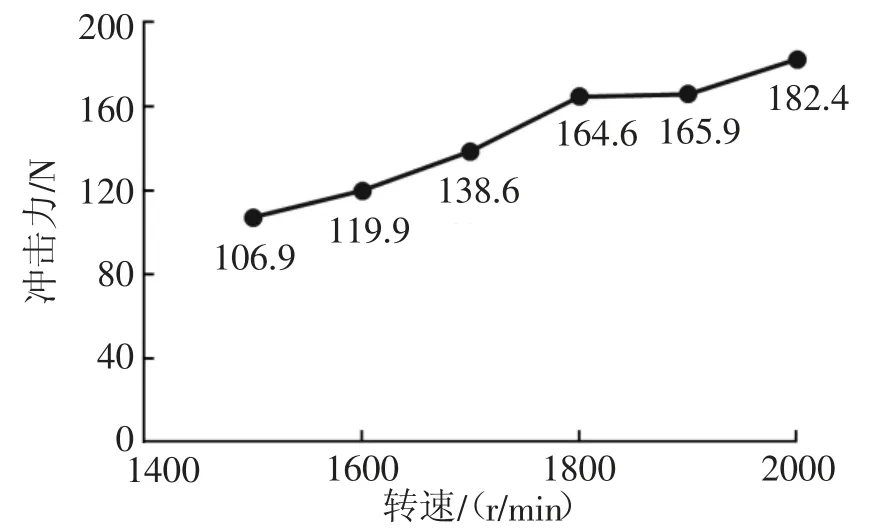
图6 不同铣刨转速对冲击力的影响
3.3 进给速度对冲击力的影响
铣刨水泥混凝土路面时,取铣刨深度为1 mm,铣刨转速为1500 r/min,进给速度为50~200 mm/s,分析不同的进给速度对冲击力的影响。
图7 为进给速度不同时冲击力峰值的对比图。总体的趋势为:随着进给速度的增加,冲击力的变化不大(约为±6%),进给速度为50 mm/s 时冲击力为106.9 N,进给速度为200 mm/s 时冲击力为103.3 N。由此可见,提高铣刨机的进给速度时,刀片对混凝土地面的冲击力变化不大,在保证施工表面质量的前提下,可以适当提高进给速度,从而提高作业效率。
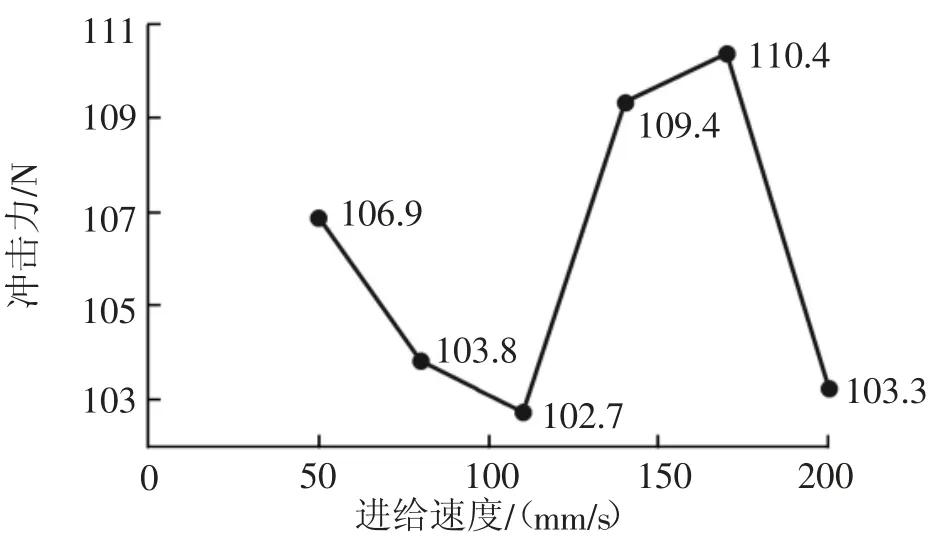
图7 不同进给速度对冲击力的影响
4 结论
本文应用ABAQUS 有限元分析软件对小型混凝土铣刨机刀片铣刨水泥混凝土过程进行有限元数值模拟,分析了不同的铣刨深度、铣刨速度、进给速度对冲击力的影响规律,为铣刨工艺研究提供了理论参考。
1)冲击力随着铣刨深度的增大而不断升高,当铣刨深度小于刀轴间隙时,铣刨深度每增加1 mm,冲击力增长5%~25%;当铣刨深度大于刀轴间隙时,冲击力急剧增加,铣刨深度每增加1 mm,冲击力增长4 倍以上。在实际施工过程中,需要保证铣刨深度小于刀轴间隙,以防因冲击力过大而造成机器故障。
2)冲击力随着铣刨转速的增加而升高,铣刨转速每增加100 r/min,冲击力增长10%~18%。
3)随着进给速度的增加,冲击力变化幅度约为±6%。提高铣刨机的进给速度时,刀片对水泥混凝土地面的冲击力变化不大,在保证施工表面质量的前提下,可以适当提高进给速度,从而提高作业效率。

