Uncertainty quantification of inverse analysis for geomaterials using probabilistic programming

Hongo Zho,Shojun Li,Xioyu Zng,Xinyi Liu,Lin Zhng,Jiolong Ren

a School of Civil Engineering and Geomatics, Shandong University of Technology, Zibo, 255000, China

b State Key Laboratory of Geomechanics and Geotechnical Engineering,Institute of Rock and Soil Mechanics,Chinese Academy of Sciences,Wuhan,430071,China

Keywords: Geological engineering Geotechnical engineering Inverse analysis Uncertainty quantification Probabilistic programming

ABSTRACT Uncertainty is an essentially challenging for safe construction and long-term stability of geotechnical engineering.The inverse analysis is commonly utilized to determine the physico-mechanical parameters.However,conventional inverse analysis cannot deal with uncertainty in geotechnical and geological systems.In this study,a framework was developed to evaluate and quantify uncertainty in inverse analysis based on the reduced-order model(ROM)and probabilistic programming.The ROM was utilized to capture the mechanical and deformation properties of surrounding rock mass in geomechanical problems.Probabilistic programming was employed to evaluate uncertainty during construction in geotechnical engineering.A circular tunnel was then used to illustrate the proposed framework using analytical and numerical solution.The results show that the geomechanical parameters and associated uncertainty can be properly obtained and the proposed framework can capture the mechanical behaviors under uncertainty.Then,a slope case was employed to demonstrate the performance of the developed framework.The results prove that the proposed framework provides a scientific,feasible,and effective tool to characterize the properties and physical mechanism of geomaterials under uncertainty in geotechnical engineering problems.

1.Introduction

In geotechnical engineering,inverse analysis is essential for determining the geological properties,geomechanical properties,and in situ stress.It has been widely used as an analysis tool for design,adjusting construction technology and optimizing the support scheme in geotechnical and geological engineering problems (Feng et al.,2004).However,due to the complex geological conditions,there are many uncertainties caused by the anisotropy and heterogeneity of geomaterials,for example the monitoring error,observation error,and simplicity of the computational model.Uncertainty is an intrinsic property in geotechnical and geological engineering.Uncertainty quantification provides an excellent way to handle uncertainty in the field of engineering.However,traditional inverse analysis cannot deal with uncertainty.

Inverse analysis has been applied to geotechnical and geological engineering over the past decades.Some researchers have proposed different inverse analysis methods using various models.These models are used to approximate and capture the complex nonlinear responses of surrounding rock mass based on the geotechnical and geological parameters (Yu et al.,2007;Zhao and Yin,2009,2016;Bozzano et al.,2012;Zhang and Yin,2014;Fazio et al.,2017;Lv et al.,2017;Sun et al.,2018).The response surface method is an excellent model to approximate the physicalmodel(Liet al.,2016a).However,it is challenging to characterize the physical model of the geotechnical structure because of the highly nonlinear relationship of the highdimensional unknown parameters(Guo et al.,2016).With development of the artificial intelligence,machine learning and soft computing were utilized to generate the surrogate model in the inverse analysis (Deng and Lee,2001;Shang et al.,2002;Feng et al.,2004;Yu et al.,2007;Zhao and Yin,2009;Zhao et al.,2015).Unfortunately,overfitting and local minimum trapping hinder the application of artificial intelligence and machine learning in geotechnical and geological engineering (Zhao et al.,2012).Moreover,the above models were only a universal approximator trained using a set of samples and did not reflect the physical mechanism of the geotechnical and geological structures (Zhao and Chen,2021).The reduced-order model(ROM)has been recently developed to capture some physical mechanisms of the engineering structure under consideration(Zhao,2021).The ROMisthe physics-baseddata-driven model and can capture well the physical mechanism of geotechnical structure.Compared with traditional and intelligent models such as artificial neural networks,support vector machines,decision trees,fewer parameters are needed in the ROM.Meanwhile,the ROM can predict the total physical field of structure responses for geotechnical engineering.This study adopted the ROM to capture the complex response based on unknown geotechnical and geological parameters.

Probabilistic technology has been applied in inverse analysis to handle uncertainty.The traditional inverse analysis usually adopts the deterministic method and ignores the uncertainty of the geomaterial parameters and monitoring information.The probabilistic inverse analysis method has been adopted to back-calculate the geomaterial parameters by combining the statistical method,inference model,and idea of inverse analysis(Li et al.,2016b;Jiang et al.,2020;Sun et al.,2021).The probabilistic inverse analysis method opens a space to extend back-calculation based on prior knowledge and field information.However,it is not easy to implement in practical engineering(Zhang et al.,2010).Uncertainty quantification provides an excellent tool to characterize uncertainty and has attracted considerable attention in engineering(Sun et al.,2021).The uncertainty quantification method is used to characterize the mechanical mechanism of a fully grouted rockbolt based on the pull-out tests(Zhang et al.,2022).This study combines uncertainty quantification with inverse analysis to capture uncertainty based on probabilistic programming.

An uncertainty quantification framework was developed in this context to characterize the geomaterial properties and the corresponding uncertainty by combining the ROM and probabilistic programming.The uncertainty quantification algorithm was implemented in the PyMC3 package,and the proposed framework was applied to analyze a circular tunnel and the Bachimen slope in Fujian Province,China.

2.Inverse analysis and ROM

2.1.Concept of inverse analysis

Sakurai and Takeuchi (1983) developed the inverse analysis technique to recognize rock properties by monitoring deformation in rock engineering.It provides a simple but effective technology to identify the properties of geomaterials,such as mechanical parameters and in situ stresses.The basic idea is to minimize the discrepancy between the monitoring response and the predicted response of the geotechnical and geological structure based on the monitoring data to obtain the unknown parameters.Fig.1 shows the framework of inverse analysis.

Fig.1.Schematics of inverse analysis.

In recent years,significant progress has been made on inverse analysis methods for geotechnical engineering(Sakurai,2017).The physical model,which characterizes the deformation and failure mechanism of the geological medium,is the main component of the inverse analysis.Numerical analysis is widely utilized to characterize the mechanical response of the geological medium (Jing and Hudson,2002).However,in practical geotechnical applications,numerical analysis is time-consuming.In order to improve the efficiency of the numerical model,ROM is regarded as an alternative in this study.

2.2.Model in inverse analysis: ROM

Due to the complexity and nonlinearity of the geotechnical and geological medium,it is impossible to obtain closed-form solutions,and numerical solutions are generally time-consuming.A model constructed based on orthogonal decomposition was utilized to approximate the response of the surrounding rock mass according to the theory of the ROM.The following equation can be obtained based on the proper orthogonal decomposition (Audouze et al.,2009):

Eq.(1) can be rewritten as follows:

where

A set of design variables,θj,is generated using Latin hypercube sampling(LHS)to obtain the basis vector φ and its coefficient β for ROM.Then,a set of the discrete responses (snapshots) of the geotechnical structure,wj=uh（θj）-（θj）,is determined using numerical models,such as the discrete element method.The spatial Gram matrix (Mx) is defined as follows:

wherewiwjdenotes the scalar product betweenwiandwj.The positive eigenvalues λ of Mxare presented in descending order:

The orthogonal principal direction of snapshots is obtained based on the firstKeigenfunctions φk（x）（k=1,2,…) Ifrk=is thekth eigenvector of Mx,then its dualkth eigenfunctions φk（x）are obtained by

whereKis the dimension of the proper orthogonal decomposition basis,can be determined as follows:

where ε is tolerance and specified by the user according to the problem.ε is generally 0.9999.

The penalized minimization method is utilized to determine the coefficient β as follows:

The parameter βjin Eq.(8) can be solved as follows:

where μ is a small regularization parameter.

To obtain the field variables of the spatial coordinatesxand unknown design variables θ,the coefficient βk（θ）is expanded based on Radial Basis Function (RBF) as follows:

where σ is the scalar parameters.

Based on the above equation,the following equation will be obtained for any θj′（j′=1,2,…,J）:

Eq.(11) can be rewritten in the compact form:

The unknown coefficient αkcan be solved using the following equation:

3.Uncertainty quantification and probabilistic programming

Recently,uncertainty quantification has been a hot topic in engineering systems (Clement et al.,2013).Uncertainty quantification has been a diverse analysis method appropriate for evaluating the uncertainty of measurements and computational processes.Since the uncertainty of fluid dynamics was evaluated by uncertainty quantification in 1986 (AIAA G-077-1998,2002),increasing attention has been paid in various engineering fields.In general,uncertainty quantification is divided into forwarding and inverse methods.The forwarding method,also called uncertainty propagation,investigates the effect of input uncertainty on the response uncertainty of engineering systems in engineering models.The inverse method evaluates the uncertainty corresponding to the properties because of the experimental,computational,measurement,and personal errors.Computational algorithms,such as polynomial chaos expansion,Karhunen-Loeve expansion,Bayesian methods,and Monte Carlo simulation,have been adopted in uncertainty quantification(Choi et al.,2007;Beck,2010;Hiriyur et al.,2011;Clement et al.,2013).In this context,probabilistic programming was employed to carry out uncertainty quantification to capture the mechanical and deformation behaviors of the surrounding rock mass under uncertainty.

Probabilistic programming,a subfield of artificial intelligence,deals with the relationship between uncertain input and output.Probabilistic programming allows the programmer to express uncertain knowledge in the form of probability distributions.It makes it possible to evaluate and quantify the uncertainty response of the engineering system from uncertain data.Probabilistic programming offers some advantages for artificial intelligence applications.They allow for the concise representation of complex models,and provide a way for uncertainty automatically.This can be compiled into efficient code.

Probabilistic programming is also a comprehensive crossover technique based on Bayesian statistics,machine learning,and process-based modeling.Probabilistic programming includes a probabilistic model and an inference algorithm.It works by building a new probabilistic reasoning model,and makes predictions and inferences about unknown things based on observations(Avi,2016).The basic idea of probabilistic programming is to represent probabilistic models by computer programs (Fig.2).The data simulator,which samples different sets of possible data based on the probabilistic model by calling the random number generator,is constructed based on a probabilistic model using probabilistic programming (Ghahramani,2015).It is easy to construct recursion and control flow statements using probabilistic programming,while it is impossible to implement using a finite graph.Any computable probability distribution can be handled by probabilistic programming.

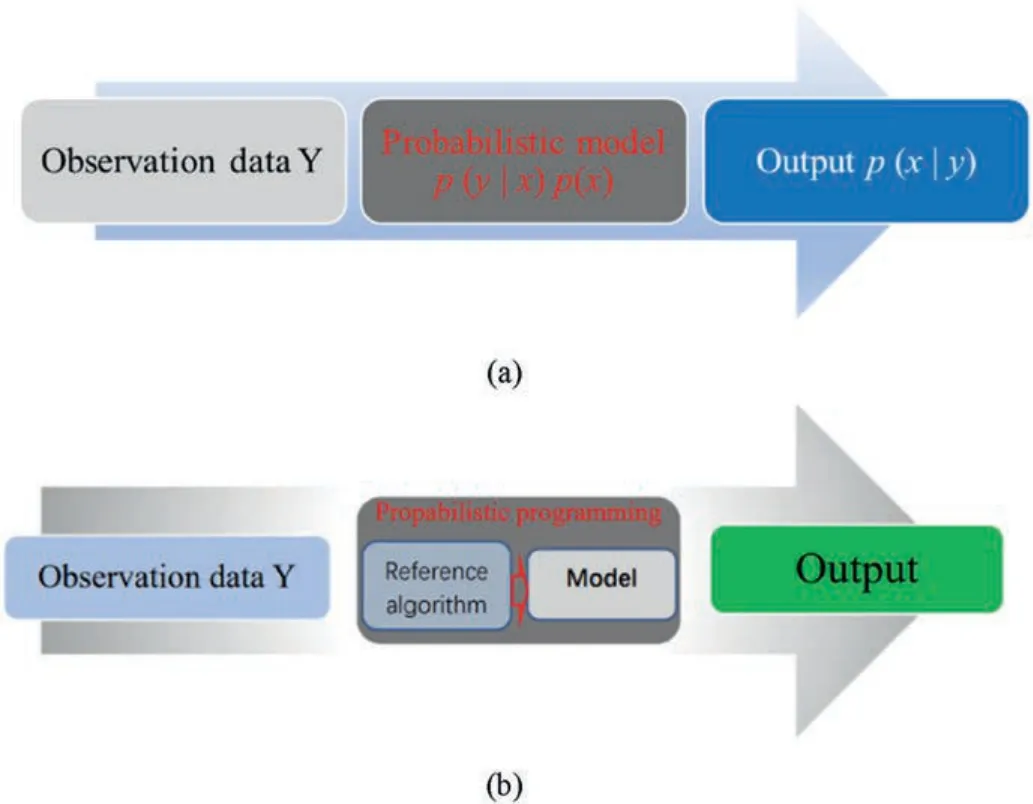
Fig.2.Probabilistic programming and statistical model: (a) Statistical model;and (b)Probabilistic programming.

Probabilistic programming can infer unobserved information from the observed data based on the physical model in an engineering system.The uncertainty of the system model can be captured by the probability feature used in the simulator.The inference algorithm can automatically infer the unknown mechanical behavior and other uncertain model parameters of the engineering system by constraining the output of the program according to the observed data.Many probabilistic programming has emerged recently,such as BUGS (Lunn et al.,2000),Stan,AutoBayes(Fischer and Schumann,2003),and PyMC3.We utilized PyMC3 to recognize the geomaterial properties and to evaluate their uncertainty.

In the past decades,various probabilistic programming systems have been built.A new generation of Markov chain Monte Carlo(MCMC) sampling techniques,such as Hamilton Monte Carlo(HMC) (Duane et al.,1987) and no-U-turn sampler (NUTS)(Hoffman and Gelman,2014),can be well adapted to high and complex posterior distributions,and many complex models can be applied without understanding fitting methods.The gradient method is utilized in HMC and NUTS to gain much higher efficiency than conventional sampling technologies,especially for largerscale problems such as those of geotechnical engineering.PyMC3 is a novel,open-source probabilistic programming package with an intuitive,readable,and powerful syntax that approximates the natural syntax statisticians use to characterize models (Salvatier et al.,2016).PyMC3 is adopted to solve general Bayesian prediction and statistical inference problems.

4.Uncertainty quantification of inverse analysis

We adopted uncertainty quantification to capture the uncertainty feature of the inverse analysis using PyMC3.The analytical model was utilized to characterize the relation between the geomaterial properties and corresponding responses of geotechnical and geological structure.PyMC3 was employed to determine the unknown geotechnical and geological parameters and to assess their uncertainty from the monitored data (prior knowledge).The mechanical behavior of the geotechnical and geological structure was evaluated and quantified by combining ROM,probabilistic programming,and field monitoring data.

4.1.ROM-based geotechnical model

To improve the efficiency of the computational model,the ROM was used to construct the computational model of geotechnical and geological engineering problems.The ROM was utilized to obtain the geotechnical and geological structure response based on the uncertainty variables.The ROM presented the relationship between the uncertainty of geomaterial property and the corresponding response.It can be presented as follows:

where X=（x1,x2,…,xn）,and xi(i=1,2,…,n) represents the geotechnical and geological parameters (such as cohesion,friction angle,Young’s modulus,and in situ stress);y represents the stress,displacement,and plastic zone.In this study,the algorithm of the ROM was programmed using Python 3.0.

4.2.Uncertainty quantification using PyMC3

To evaluate the uncertainty of inverse analysis,PyMC3 was adopted to evaluate the response of the geotechnical structure and the corresponding uncertainty based on the monitoring data and the surrogated model (ROM).The predicting deformationuis presented in normally distributed observations.The expected value σuis a nonlinear function of the uncertainty of the unknown variable of the geomechanical model.It can be approximated by the ROM as follows:

We applied uniform distribution [Xl,Xu] to geotechnical and geological parameters (X).XlandXuare the lower and upper bounds ofX,respectively.The uniform distribution corresponds to the weak information of actual unknown geomaterial parameters.According to the nature of geotechnical and geological engineering problems,some other distributions such as normal distribution can also be adopted based on the obtained information:

By using PyMC3 to specify the above model,a posterior estimation of unknown geotechnical and geological parameters is computed based on the ROM in the next step.Depending on the objective of the problem and the structure of the model,there are two ways to determine the regression coefficients,namely using an optimization method to find the maximum a posteriori(MAP)and using the MCMC sampling method to calculate a summary of the sample based on the posterior distribution.

4.3.Procedure

The flowchart of the proposed framework is presented in Fig.3.The detailed procedure is as follows.

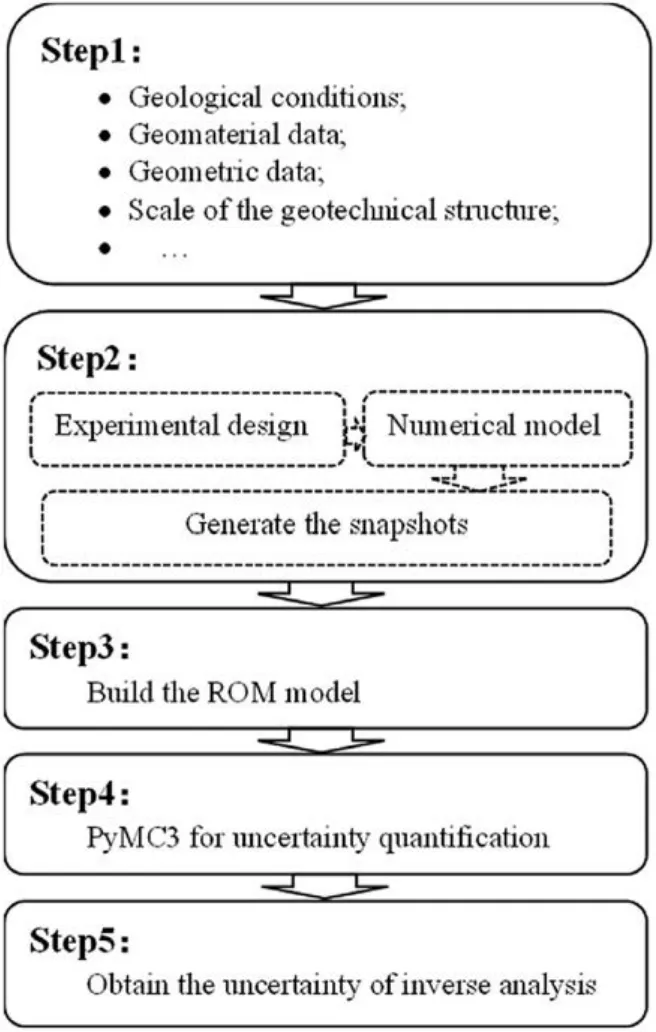
Fig.3.The flowchart of the proposed framework.

(1) Collect the projection data,including geological conditions,geomaterial data,geometric data,and scale of the geotechnical and geological structure,

(2) Construct the numerical model and generate snapshots based on the experiment design technology,

(3) Build the ROM based on the snapshots,

(4) Conduct the uncertainty quantification using PyMC3 based on probabilistic programming,and

(5) Obtain and quantify the uncertainty of geotechnical and geological parameters and their response.

5.Verification

A tunnel was utilized to verify and demonstrate the proposed framework.The shape of the tunnel is circular,and the rock is homogeneous,continuous,and isotropic.It is excavated under hydrostatic far-field stressp0and uniform support pressurepi(see Fig.4).Duncan Fama(1993)used the Mohr-Coulomb(M-C)model to study the deformation of tunnel walluipduring excavation:

Fig.4.A circular tunnel under hydrostatic far-field stress.

whereE,v,andrpare the elastic modulus,Poisson’s ratio,and plastic zone radius,respectively.The values ofpcr,k,s,andrpcan be determined by

wherecand φ are the cohesion and friction angle of the rock,respectively;pcris the critical pressure that determines whether or not a plastic zone occurs.A plastic zone will appear whenpiis less than the critical pressurepcr.

The radius of the tunnel is 1 m.TheE,v,c,and φ are 6800 MPa,0.2,3.2 MPa,and 32°,respectively.The in situ stress is 32 MPa.The radial deformations of five monitoring points (see Fig.4),with distances of 1 m,1.2 m,1.6 m,1.8 m,and 2 m from the center of the tunnel,are utilized to identify the mechanical parameters of rock mass in the circular tunnel.The synthetic displacements of five monitoring points can be calculated from the above analytical solution and are chosen as the monitoring data to characterize the mechanical property of the surrounding rock mass.

5.1.Analytical solution

Based on the proposed framework,the in situ stresses and geomechanical parameters (p0,E,c,and φ) of rocks were determined using the five synthetic displacements based on the analytical solution (Eq.(19)) and probabilistic programming.Table 1 presents the obtained mean value,corresponding uncertainty,and their comparisons.The maximum relative error between the obtained mean value and actual value is less than 6%.This shows that the framework can be adopted to compute the mean value of the rock mechanical parameters.The proposed framework is an excellent tool for inverse analysis.

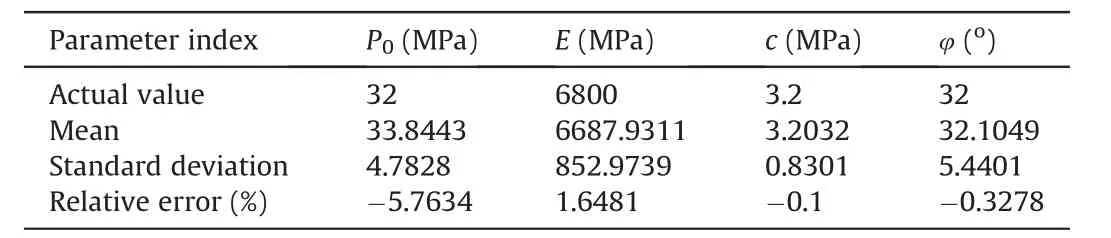
Table 1 Obtained mechanical parameters and their comparison with the actual properties.

Fig.5a compares the deformation curves of surrounding rock mass using actual parameters and the obtained mean values.The maximum relative error is less than 7%.The comparison between the stress curves of surrounding rock mass using the determined mean values and actual parameters is shown in Fig.5b,which shows that the proposed framework aptly characterizes the rock mechanical behavior in the tunnel based on the M-C model.The results further prove that the proposed framework can effectively identify the mechanical properties of rock using the displacement of the surrounding rock mass.

Fig.5.Comparison between the actual values and those obtained by the proposed framework: (a) Displacement of the surrounding rock mass;and (b) Stress of the surrounding rock mass.

The rock mechanical parameters and their uncertainty are exhibited in Fig.6.The proposed framework obtains the mean value and variance of mechanical parameters.Our investigations show that the proposed framework can capture the uncertainty of rock mechanical parameters by considering the monitoring information.This is helpful and useful for information construction and design of rock tunnels.Fig.7 illustrates the uncertainty of the deformation curve obtained by the proposed framework.The framework can characterize the uncertainty of the deformation induced by tunnel excavation.Moreover,it can characterize the deformation of the rock mass better than traditional inverse analysis.

Fig.6.Uncertainty distribution of rock mass mechanical parameters and the actual values: (a) In situ stress;(b) elastic modulus;(c) cohesion;and (d) friction angle.

Fig.7.The displacement curve of the surrounding rock mass and its uncertainty.

To investigate the robustness of the proposed framework,different uniform distributions were illustrated based on probabilistic programming.Three different search ranges cover the actual value of the unknown parameters,but the interval size of the three ranges is different.Table 2 presents the different uniformdistributions.Table 3 presents the identified rock mechanical parameters based on the proposed framework.The maximum relative error is less than 9%.Meanwhile,the relative error will decrease with the narrowing of the search ranges.The deformation curve of the surrounding rock mass is displayed in Fig.8 based on different uniform distributions,which shows that the framework has a good performance in terms of robustness.Fig.9 reveals the uncertainty variation of the surrounding rock mass,which is determined based on the different prior distributions using the proposed framework.It is clear that the distribution will narrow with decrease of the uniform distribution range.This proves that more information can be helpful and reduce the uncertainty of the unknown parameters.These observations suggest that the proposed framework is robust and has good global searching performance.

Table 2 Different range of uniform distributions for unknown parameters.

Table 3 The obtained results based on different uniform distributions.

Fig.8.The displacement curves of the surrounding rock mass and its uncertainty.

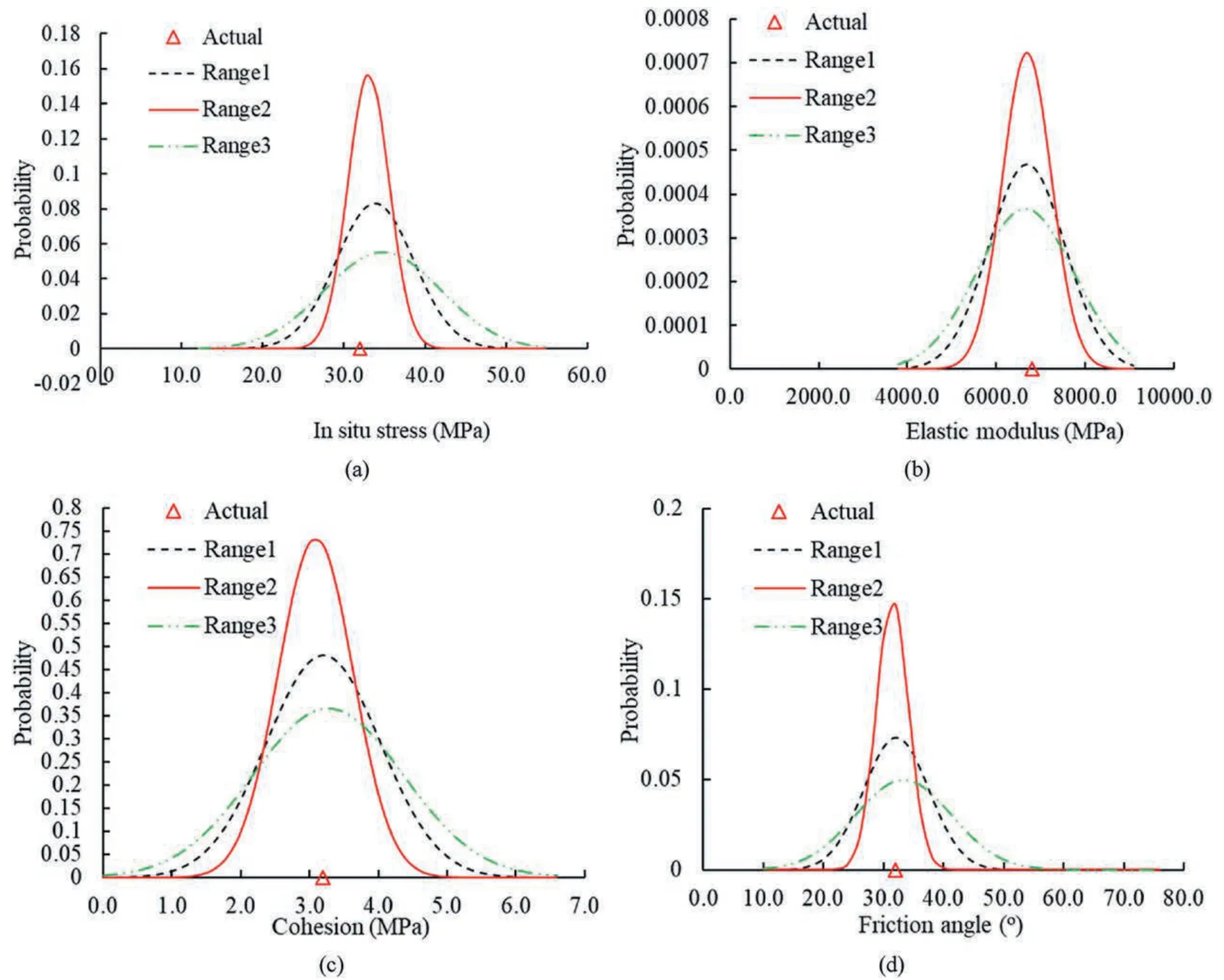
Fig.9.The displacement curves of the surrounding rock mass and its uncertainty: (a) In situ stress,(b) elastic modulus,(c) cohesion,and (d) friction angle.

5.2.ROM-based model

We utilized the ROM to characterize the rock mass response induced by the tunnel excavation.Fifty snapshots were constructed using the analytical solution.ROM was generated based on the 50 snapshots.The other 50 non-snapshots were utilized to demonstrate the ROM’s performance.Fig.10 depicts the relationship between the rock mass response and mechanical parameters using the analytical solution and ROM.Fig.11 displays the sensitivity of the unknown mechanical parameters to the rock mass response.As observed,the ROM is almost identical to the analytical model.Fig.12 compares the ROM and analytical solution.Our investigations prove that the ROM can capture the rock mechanical behavior well.It is feasible to predict the rock mass response during the excavation using ROM instead of analytical and numerical solutions.

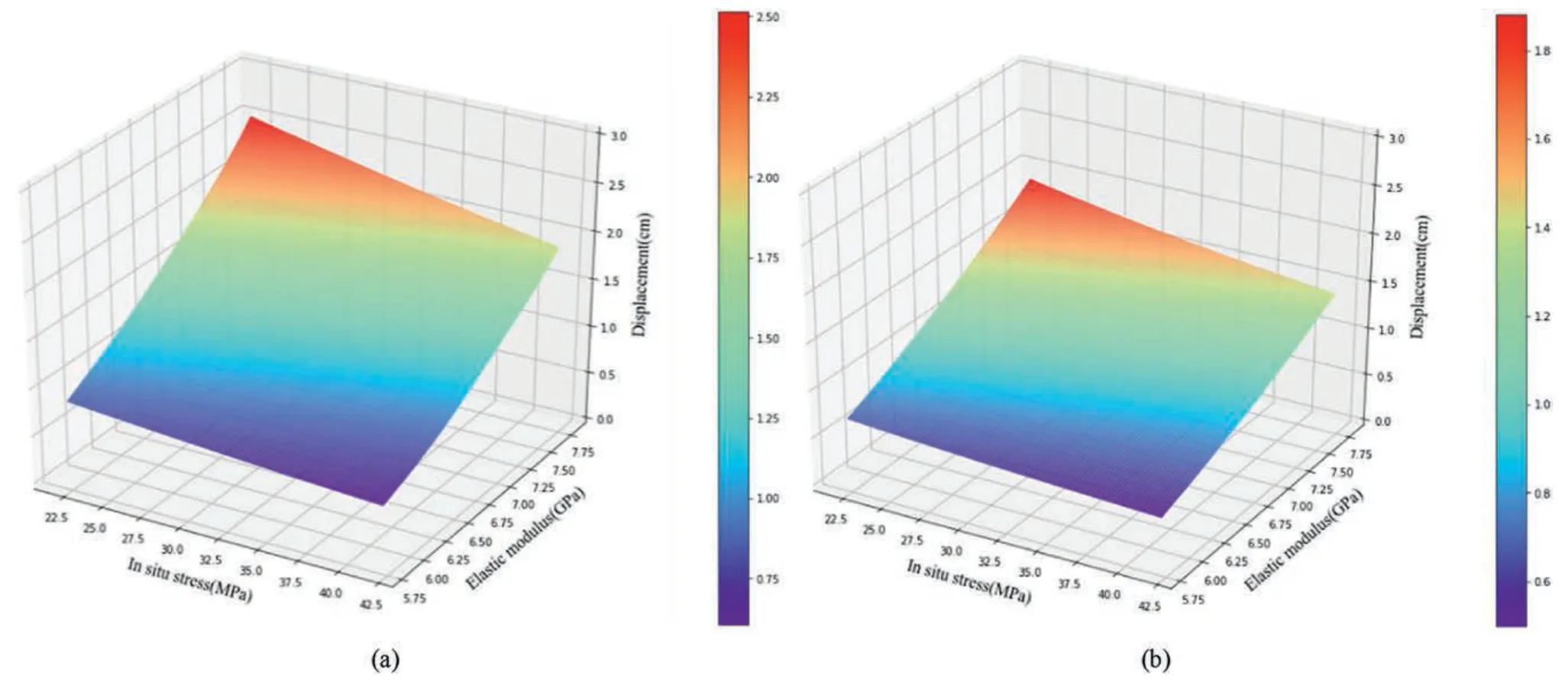
Fig.10.The in situ stress,elastic modulus,and displacement based on the analytical solution and the ROM: (a) Analytical solution,and (b) ROM.

Fig.11.The sensitivity of the unknown parameters to the rock mass response using the analytical solution and the ROM(Note:ST is the total sensitivity:(a)Analytical solution,and(b) ROM).

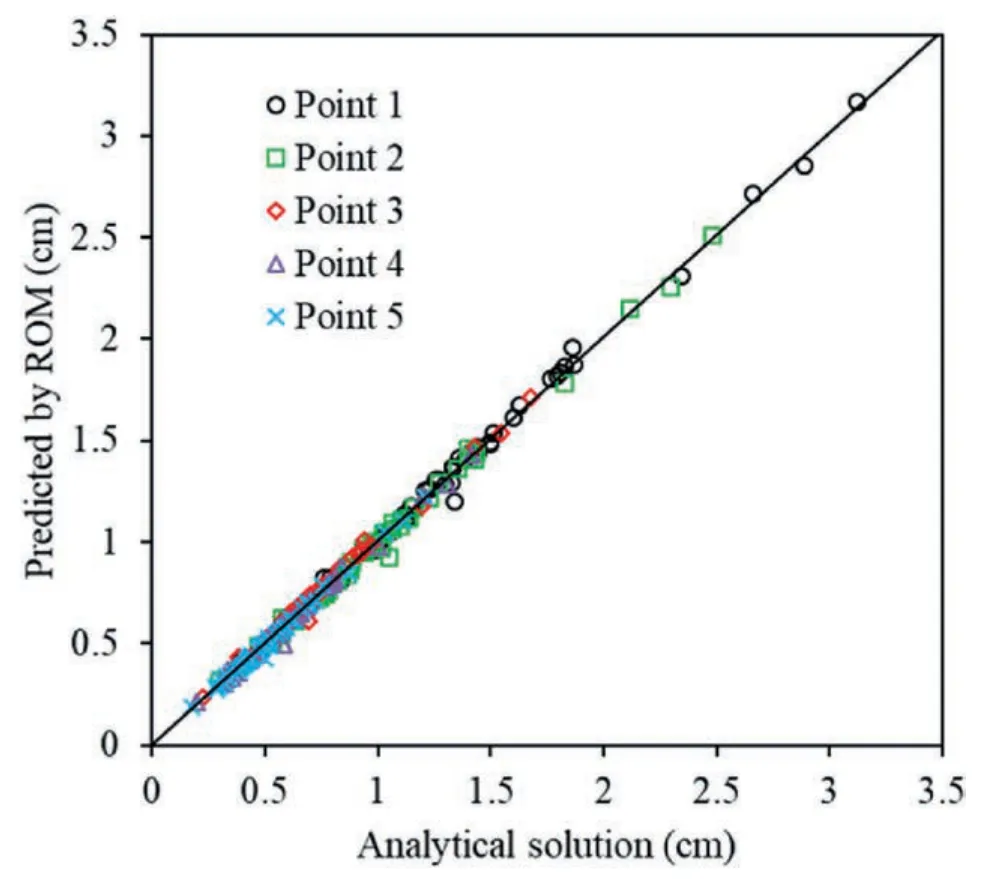
Fig.12.The displacement comparison between the analytical solution and ROM.

While the ROM was built,probabilistic programming was employed to acquire the rock mechanical parameters and their corresponding uncertainty.The results are presented in Table 4.The results show that the obtained rock mechanical parameters are in excellent agreement with the real values.The maximum relative error is less than 4.5%.Fig.13 shows the comparison of displacement and stress.It proves that the ROM can capture the rock mechanical mechanism well.It also proves that the ROM could replace the analytical model in the proposed framework,which is conducive to practical rock engineering.

Table 4 The obtained results based on the ROM.

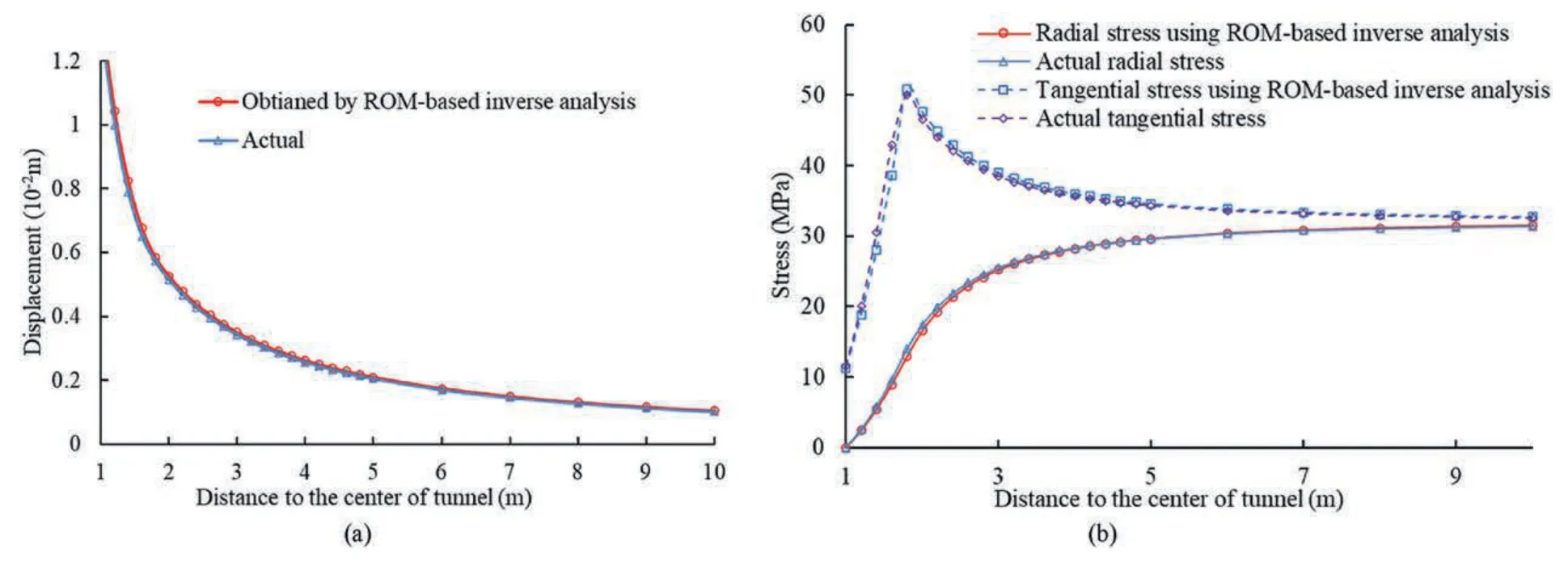
Fig.13.The rock mechanical behavior based on the rock mechanical properties obtained by the proposed framework: (a) Displacement,and (b) Stress.

We utilized PyMC3 to characterize the uncertainty of the unknown parameters based on probabilistic programming.Theuncertainty of the mechanical parameters for the rock mass is shown in Fig.14.The rock mechanical parameters almost follow the normal distribution.The uncertainty of the objective function error is displayed in Fig.15,which meets the normal distribution.

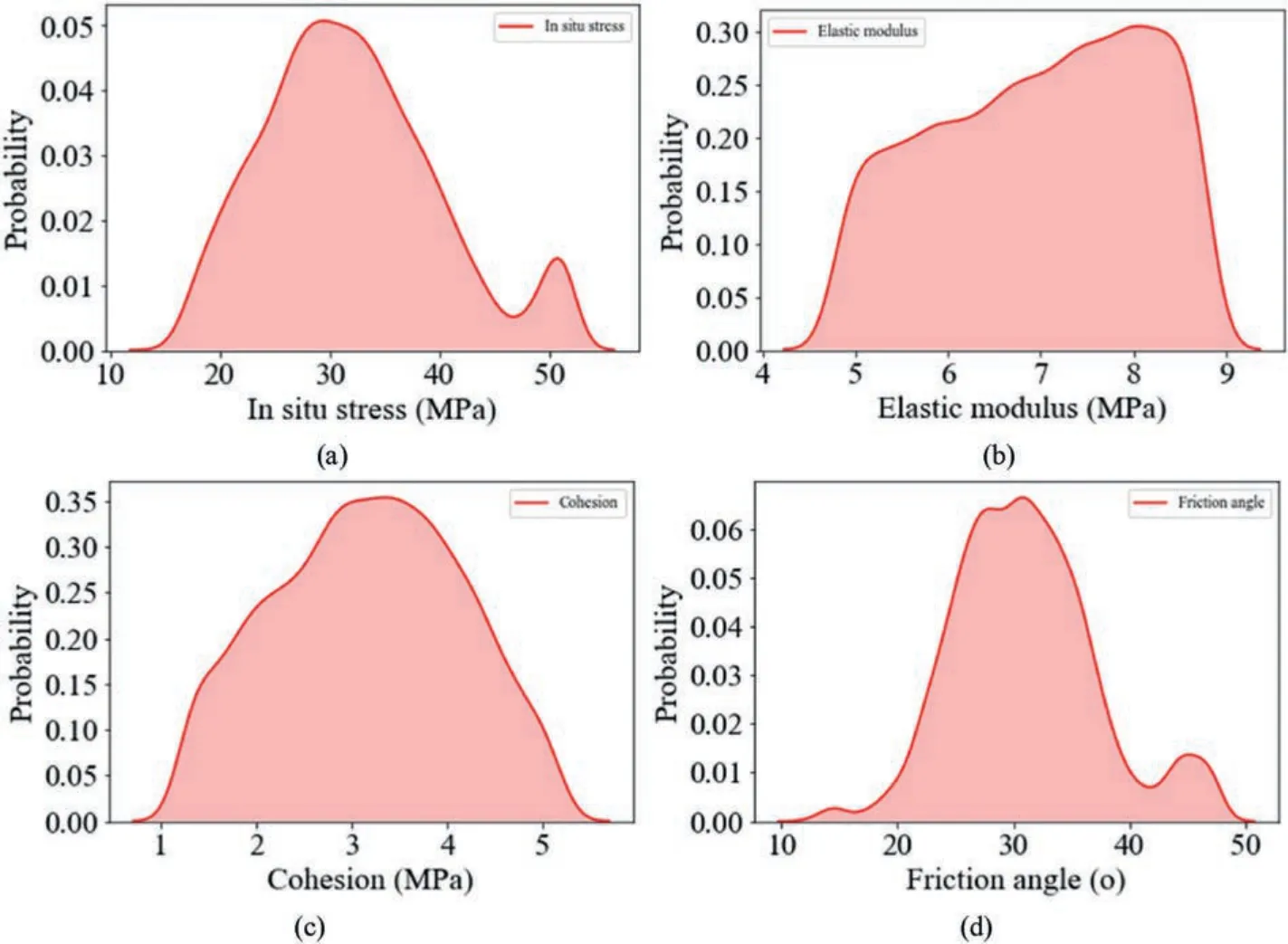
Fig.14.The displacement curve of the surrounding rock mass and its uncertainty: (a) In situ stress,(b) elastic modulus,(c) cohesion,and (d) friction angle.

Fig.15.The displacement curve of the surrounding rock mass and its uncertainty.

6.Case study

This section applies the proposed framework to the Bachimen slope.This slope was induced by the construction of the Funing expressway,which is located in Fujian Province,China(Feng et al.,2004).To avoid landslides and maintain stability during construction,the mechanical parameters of geomaterials are critical for Bachimen slope.The inclinometers have been installed at 60 boreholes to monitor displacements of the slope.This study adopted the proposed framework to identify the geomechanical and strength parameters(Young’s modulus,cohesion,and internal friction angle)and corresponding uncertainty based on the data of inclinometers during construction.The deformation values at different positions of inclinometer boreholes (BCX05 and BCX07)(Fig.16) are regarded as prior knowledge using probabilistic programming.

Fig.16.Inclinometer boreholes of BCX05 and BCX07 at Bachimen slope.

The numerical model (finite element method) was adopted to compute the deformation at different positions of the boreholes(BCX05 and BCX07).To build the ROM,50 snapshots and 10 validation samples were generated using the ortho-experimental design and numerical model.The ROM was constructed using 50 snapshots based on the proposed framework.Then,the ROM was validated and tested using the above 10 validation samples.Fig.17 exhibits the comparison of the displacement calculated by the numerical model and that predicted by the ROM.Our investigations demonstrate that the ROM aptly captures the deformation characteristics of the geomaterials in Bachimen slope.

Fig.17.Comparison of displacement computed by numerical model and predicted by the ROM.

The proposed framework was used to determine the unknown geomechanical parameters,with prior knowledge being a uniform distribution,as tabulated in Table 5.Table 6 presents the obtained results.Fig.18 depicts the uncertainty of the mechanical parameters of geomaterials.It shows that Young’s modulus of the sub-clay layer is of normal distribution,and other mechanical parameters have a uniform distribution.Based on the obtained geomechanical parameters,our framework predicted the horizontal displacements of boreholes BCX5 and BCX7.The results are displayed in Fig.19.For the borehole BCX7,the predicted displacement is in excellent agreement with the monitoring displacement,and the absolute error of the predicted displacement is less than that of the borehole BCX5.However,the maximum relative error of the borehole BCX5 is 13.83%.The results confirm that the proposed framework can identify geomechanical parameters in geotechnical engineering fields.

Table 5 The range of geomechanical parameters.

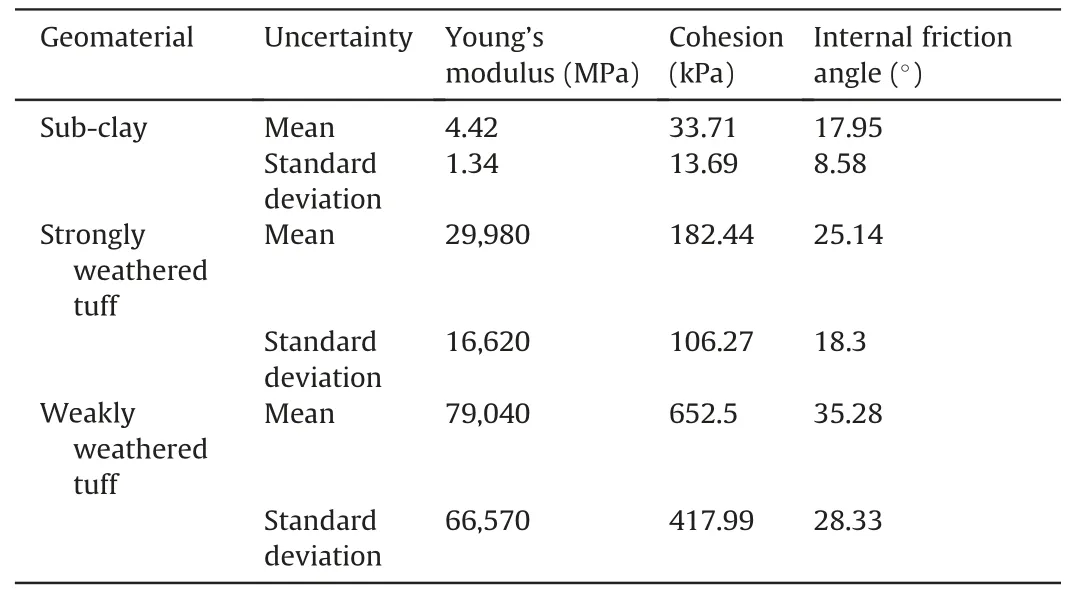
Table 6 The obtained mechanical parameters of geomaterials.

Fig.18.The uncertainty of the obtained mechanical parameters of geomaterials: (a) Young modulus of sub clay,(b) Cohesion of sub clay,(c) Friction angle of sub clay,(d) Young modulus of strongly weathered,(e) Cohesion of strongly weathered,(f) Friction angle of strongly weathered,(g) Young modulus of weakly weathered,(h) Cohesion of weakly weathered,and (i) Friction angle of weakly weathered.

Fig.19.Displacement comparison between predicted by ROM and monitored: (a) BCX07,and (b) BCX05.

In geotechnical and geological engineering,the monitoring error exists in the geotechnical and geological responses and can induce uncertainty of displacements.The displacement errors are shown in Figs.20 and 21 for the boreholes BCX5 and BCX7,respectively.The monitoring error has a significant impact on the deep displacement of the slope.Therefore,monitoring accuracy is essential for evaluating and quantifying the geomechanical parameters.In Figs.20 and 21,the predicted mean values of displacement at depths of 10mand 15 m (Fig.20c and d) are in excellent agreement with the monitoring value,but there are some differences at depths of 0mand 2 m(Fig.20a and b and Fig.21).The shallow monitoring points have a broader distribution than that of deep monitoring points in the borehole.This induces more significant error and uncertainty.It suggests that the data of deep monitoring points are essential and we should be pay more attention to the geotechnical and geological fieldwork.In order to better describe the geomechanical characteristics of surrounding rock,monitoring the deformation of deep surrounding rock is helpful and valuable in geotechnical engineering.

Fig.20.Displacement comparison under different monitoring errors at borehole BCX7: (a) Monitoring position of 0 m,(b) Monitoring position of 2 m,(c) Monitoring position of 10 m,and (d) Monitoring position of 15 m.

Fig.21.Displacement comparison under different monitoring errors at borehole BCX5: (a) Monitoring position of 0 m,and (b) Monitoring position of 5 m.

7.Conclusions

Determining the geomechanical and geological parameters is essential to the stability,design,support,and construction in geotechnical engineering.Inverse analysis is an effective method for this and is widely applied in practical engineering.However,failure and instability events still exist due to the uncertainty of geotechnical and geological engineering problems.For this,we proposed a framework for quantifying uncertainty in inverse analysis.The framework could determine the geomechanical properties under uncertainty by combining probabilistic programming,numerical model,inverse analysis,and field monitoring data.The actual cases (a tunnel and a slope) demonstrated the correctness of the proposed framework.The geomechanical parameters of the surrounding rock mass and their uncertainty were obtained using PyMC3.Based on the uncertainty of the geomechanical parameters,the uncertainty of the geomechanical behavior was evaluated and quantified using the proposed framework.Our investigations indicate that the developed framework can effectively evaluate the uncertainty of the geomechanical behavior.Therefore,it provides an excellent tool for quantifying the uncertainty of geotechnical and geological structures and scientifically captures the mechanical mechanism of geomaterials with uncertain parameters.The proposed framework is conducive to feedback analysis,guiding safe construction,and reliability-based designs of geotechnical and geological structures.The following conclusions are drawn in this study.

(1) The proposed framework provides a rational,scientific,and feasible way to deal with the uncertainty of geotechnical and geological engineering.A circular tunnel with an analytical solution and a practical slope with the numerical solution verified and illustrated the framework.

(2) The ROM is utilized to characterize the mechanical response of surrounding rock mass.It captures the nonlinear,highdimensional,and complex relationship between the geotechnical parameters and mechanical response.It provides an excellent tool for characterizing the geomaterial behavior in geotechnical engineering.The ROM depends on the snapshots obtained from the numerical model in this study.To obtain the excellent surrogated model for inverse analysis,numerical model that can characterizes the mechanical behavior and boundary conditions of the practical application is essential in the ROM.

(3) The monitoring data reflect the mechanical and deformation properties of surrounding rock mass,in situ stress,and geological conditions.The proposed framework makes full use of the monitoring data to explore mechanism of failure and deformation.In practical geotechnical engineering,the developed method can replace the traditional inverse analysis method to determine the geomaterial properties based on in situ monitoring data.

(4) Probabilistic programming is an excellent tool for dealing with uncertainty based on the Bayesian theory.PyMC3 is an easy and friendly package for probabilistic programming in Python and is suitable for complex problems such as those of geotechnical and geological engineering.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors gratefully acknowledge the support from the National Natural Science Foundation of China (Grant No.42377174),the Natural Science Foundation of Shandong Province,China(Grant No.ZR2022ME198) and the Open Research Fund of State Key Laboratory of Geomechanics and Geotechnical Engineering,Institute of Rock and Soil Mechanics,Chinese Academy of Sciences (Grant No.Z020006).