Anisotropic strength,deformation and failure of gneiss granite under high stress and temperature coupled true triaxial compression
Hongyuan Zhou,Zaobao Liu,Fengjiao Liu,Jianfu Shao,Guoliang Li
a Key Laboratory of Ministry of Education on Safe Mining of Deep Metal Mines, College of Resources and Civil Engineering, Northeastern University, Shenyang,110819, China
b Institute of Deep Engineering and Intelligent Technology, Northeastern University, Shenyang,110819, China
c University Lille, CNRS, Centrale Lille, UMR 9013-LaMcube-Laboratoire de Mécanique, Multiphysique, Multi-échelle, F-59000, Lille, France
d State Key Lab on Rail &Transit Engineering Informatization, China Railway First Survey and Design Institute Group Co.Ltd, Xi’an, 710043, China
Keywords: Anisotropic strength and deformation True triaxial compression Thermal mechanical coupling Deep rock mechanics High temperature rock mechanics
ABSTRACT The anisotropic mechanical behavior of rocks under high-stress and high-temperature coupled conditions is crucial for analyzing the stability of surrounding rocks in deep underground engineering.This paper is devoted to studying the anisotropic strength,deformation and failure behavior of gneiss granite from the deep boreholes of a railway tunnel that suffers from high tectonic stress and ground temperature in the eastern tectonic knot in the Tibet Plateau.High-temperature true triaxial compression tests are performed on the samples using a self-developed testing device with five different loading directions and three temperature values that are representative of the geological conditions of the deep underground tunnels in the region.Effect of temperature and loading direction on the strength,elastic modulus,Poisson’s ratio,and failure mode are analyzed.The method for quantitative identification of anisotropic failure is also proposed.The anisotropic mechanical behaviors of the gneiss granite are very sensitive to the changes in loading direction and temperature under true triaxial compression,and the high temperature seems to weaken the inherent anisotropy and stress-induced deformation anisotropy.The strength and deformation show obvious thermal degradation at 200 °C due to the weakening of friction between failure surfaces and the transition of the failure pattern in rock grains.In the range of 25 °C-200 °C,the failure is mainly governed by the loading direction due to the inherent anisotropy.This study is helpful to the in-depth understanding of the thermal-mechanical behavior of anisotropic rocks in deep underground projects.
1.Introduction
Anisotropic rocks exist commonly in deep engineering constructions,such as tunnel construction (Tonon and Amadei,2014;Mambou et al.,2015;Chen et al.,2017),oil and shale gas extraction(Gao et al.,2015;Yang et al.,2020;Kasyap and Senetakis,2022),radioactive waste disposal(Millard et al.,2013;Young et al.,2020;Zhang and Talandier,2023),and geothermal energy extraction(Wang et al.,2022a).It is known that the rock mass is often in a high geo-stress and high geo-temperature environment in the context of deep excavation (Wang et al.,2022b;Kang et al.,2023;Liu et al.,2023).Due to high geo-stress and high geo-temperature,the excavation of anisotropic rock mass often leads to engineering problems such as rockburst (Chen et al.,2014;Dammyr,2016),spalling (Dammyr,2016),and large deformation (Hu et al.,2021).Therefore,for the safe construction and operation of underground projects,it is necessary to fully investigate the mechanical behavior of anisotropic rocks under high stress and high temperature coupled conditions.
In the past decades,numerous laboratory experiments have been conducted on anisotropic rocks to study the influence of structural anisotropy on strength,deformation,and failure behavior.Shale(Cho et al.,2012;Bonnelye et al.,2017;Wang et al.,2018;Yang et al.,2019,2020),slate(Attewell and Sanford,1974;Tan et al.,2014;Chen et al.,2017;Alejano et al.,2021),layered sandstone(Yin and Yang,2018;Li et al.,2021),schist(Nasseri et al.,1997;Cho et al.,2012;Özbek et al.,2018),gneiss(Rosch et al.,2000;Nasseri et al.,2003;Cho et al.,2012),phyllite (Ramamurthy et al.,1993;Xu et al.,2018),and claystone (Niandou et al.,1997;Liu et al.,2015,2018;Zhang et al.,2019;Braun et al.,2020) are among the most commonly studied anisotropic rocks.Brazilian splitting(Cho et al.,2012;Tan et al.,2014;Yin and Yang,2018;Yang et al.,2019),uniaxial compression(Nasseri et al.,1997;Rosch et al.,2000;Cho et al.,2012;Hou et al.,2016;Chen et al.,2017;Wang et al.,2017,2018;Yin and Yang,2018;Yang et al.,2020),triaxial compression (McLamore and Gray,1967;Attewell and Sanford,1974;Ramamurthy et al.,1993;Niandou et al.,1997;Nasseri et al.,2003;Bonnelye et al.,2017;Chen et al.,2017;Xu et al.,2018;Braun et al.,2020;Yang et al.,2020;Alejano et al.,2021;Lu et al.,2022),and triaxial tensile tests (Liu et al.,2019a;Zhang et al.,2019) are the most widely used experimental methods.The results obtained provide a good understanding of the mechanical behaviors of anisotropic rocks under an axisymmetric stress state(σ1>σ2=σ3).In the deep underground,however,the nonaxisymmetric stress state (σ1>σ2>σ3) often exists around an excavation face (Stacey and Wesseloo,2022).Therefore,the mechanical properties measured at the axisymmetric stress state can only be applied in special field conditions (Haimson and Bobet,2012;Liu et al.,2022a;Ma et al.,2023).To overcome this limitation,true triaxial compression tests (σ1>σ2>σ3) have been carried out on gneiss (Liu et al.,2020,2022a,2022b),schist (Mogi,2006),shale (Vachaparampil and Ghassemi,2017),layered limestone(Zhou et al.,2016b),and layered sandstone (Cyrille Couture and Bésuelle,2023).It has been confirmed that the strength,deformation,and failure of anisotropic rocks are influenced not only by the magnitude but also by the loading direction of the intermediate principal stress (Mogi,2006;Xie et al.,2022;Cyrille Couture and Bésuelle,2023).Due to the coupling of inherent anisotropy and stress-induced anisotropy,the failure behavior of the anisotropic rocks in true triaxial compression was found to be more complex than that in uniaxial and triaxial compression.In the presence of bedding planes,an unusual failure mode,shear failure parallel to the direction of the minimum principal stress (σ3) has been observed in the true triaxial compression tests of anisotropic rocks(Mogi,2006).So far,the relationship between this failure,strength and deformation is unclear.In addition,the quantitative identification of this failure is crucial in deep excavation.However,attention has not been paid to this issue,and thus further study is needed.
On the one hand,the strength,deformation,and failure behavior of anisotropic rocks at high temperatures is a key concern in deep underground engineering(Liu et al.,2023).Currently,hightemperature uniaxial and triaxial compression tests have been carried out on typical anisotropic rocks including oil shale (Wang et al.,2021),Tournemire shale (Masri et al.,2014),layered sandstone(Meng et al.,2018),and argillite rock(Zhang et al.,2013).The effect of temperature on strength,deformation,and failure of anisotropic rocks under axisymmetric stress states have been analyzed in these former studies.However,the mechanical behavior of anisotropic rocks under true triaxial compression and high-temperature coupled conditions,as far as we know from the published materials,has not been studied yet.The relationship between temperature and stress-induced anisotropy remains unexplored.
To address these issues,the present study conducts a comprehensive series of high-temperature true triaxial compression tests in gneiss granite.The test was completed using the self-developed thermal-mechanical coupling true triaxial test system for hard rock.We aim for clarifying the effect of temperature and principal stress directions on strength and deformation anisotropy.We also characterize the anisotropic failure behavior of gneiss granite under high-temperature true triaxial compression.The deformation evolution during deviatoric stress loading is analyzed,and a method for quantitative identification of failure modes is studied.
2.Material and methods
2.1.Site geological condition
The samples were taken from a deep tunnel in China.The surrounding rocks of this tunnel are mainly diorite,monzonite,and gneiss granite,with gneiss granite comprising more than 80%of the composition.The tunnel is buried at a depth greater than 500 m,with a maximum depth of 1558 m.The in situ stress measurements show that the average value of the maximum horizontal principal stress is about 20 MPa.
Some geological boreholes were drilled to measure the geothermal gradient in the tunnel site and it was found that at a depth range of 115-779 m,the geothermal gradient ranges from 4.13°C/100 m to 11.98°C/100 m.Additionally,there are hot springs in the tunnel site area and its adjacent areas,with a maximum temperature of 92°C.Therefore,the surrounding rocks of the studied tunnel are situated in an environment of high-ground temperature and high-stress.
The representative rock core,approximately 6 cm in diameter and 85 cm in length,is shown in Fig.1,and the gneiss granite displays a layered structure and the angle between the bedding and the core axis is about 60°.Due to the layered structure,the strength and deformation of the gneiss granite may exhibit significant anisotropy.Therefore,it is necessary to investigate the anisotropic mechanical behavior of the gneiss granite under high-temperature and high-pressure conditions.

Fig.1.The representative rock core.
2.2.Sample preparation
According to the method for rock true triaxial compression recommended by International Society for Rock Mechanics and Rock Engineering (ISRM) (Feng et al.,2019a),cuboid specimens with a height of 50 mm and the ratio of height to width of two are prepared based on the gneiss granite core shown in Fig.1c.Gneiss granite samples are cut by a diamond wire saw and polished at each side.To investigate the influence of loading orientation on the strength and failure behavior of the gneiss granite,samples with different bedding orientations are prepared.The definition of the principal stress orientation and the representative samples is depicted in Fig.2.The orientation of intermediate principal stress(σ2) is the angle ω between intermediate principal stress and the strike of the bedding.The orientation of maximum principal stress(σ1) is the angle β between maximum principal stress and the sample’s axis.

Fig.2.The definition of the principal stress orientation and the representative samples.
Before the testing,the geometry and mass of each specimen are measured.Then,the samples with a geometrical error of±0.1 mm and a density of 2.81-2.83 g/cm3are selected as the final tested sample.The mineral composition and microstructure of the samples are identified by polarized light scanning,as shown in Fig.3.The gneiss granite consists of 50% plagioclase (PI),20% alkali feldspar (Afs),10% quartz (Q),10% biotite (Bt),and 10% Hornblende(Hbl).The plagioclase and alkali feldspar have a grain size primarily ranging from 0.3 mm to 1 mm,while hornblende,quartz,and biotite have particle sizes of 0.15-0.8 mm,0.4-1.2 mm,and 0.08-0.3 mm,respectively.As a result,the gneiss granite has a medium-coarse-grained structure.

Fig.3.The result of polarized light scanning of the gneiss granite: (a) Matrix and (b) Bedding.
2.3.Experimental device
The true triaxial compression tests with real-time high temperature are realized in an auto-compensated thermo-mechanical true triaxial system (see Fig.4) designed at the Key Laboratory of the Ministry of Education on Safe Mining of Deep Metal Mines of Northeastern University (Liu et al.,2021;Wang et al.,2022a).The test system is mainly composed of four modules: rigid loading module,confining pressure loading module,temperature loading module,and system software.

Fig.4.Thermal-mechanical true triaxial testing system and its deformation measurement method: (a) High temperature true triaxial test system;(b) Schematic diagram of the loading cell;and (c) Deformation measuring apparatus.
The maximum principal stress and intermediate principal stress are applied by the rigid loading module with a precision of 0.1 kN.The minimum principal stress is applied and maintained by the confining pressure loading module with a precision of 0.1 MPa.The real-time temperature is provided and maintained by the temperature loading module.The system software is used for experiment control and data acquisition.The test system can provide a maximum test force of 2000 kN,a maximum confining pressure of 70 MPa,and a maximum temperature of 250°C for carrying out coupled thermal-mechanical as well as permeability tests of rocks in the context of geothermal energy extraction,radioactive waste disposal,oil and shale gas extraction,etc.
As presented in Fig.4,three linear variable differential transformers (LVDT) are used to measure the deformation in the directions of minimum principal stress,intermediate principal stress,and maximum principal stress,respectively.The measurement range of LVDT is ±2.5 mm,and the measurement accuracy is ±1 μm.
2.4.Experimental program
The testing conditions and physical properties of the tested gneiss are summarized in Table 1.Three groups of true triaxial compression tests are designed to investigate the effects of principal stress orientation and temperature on the anisotropic mechanical behaviors.As shown in Table 1,the first group of tests aims to investigate the influence of the maximum principal stress direction,while the second group devotes to investigating the influence of the intermediate principal stress direction.The last group focuses on investigating the impact of temperature.The testing conditions are determined based on the following considerations.

Table 1 Some physical properties of samples and relative testing conditions.
Geological exploration shows that the maximum horizontal principal stress in the area where the rock core is extracted is about 20.2 MPa,and the representative stress ratio is 1.5.Therefore,a minimum principal stress of 20 MPa and an intermediate principal stress of 30 MPa are applied in each true triaxial test.
The principal stress orientations,the angles between the principal stresses and bedding planes (see Fig.2),are applied to describe the geometrical relations between the orientations of in situ stress and the strike of the rock formation.According to the outcomes of the site geological survey,the principal stress orientations with β=60°and ω=45°are determined as representative ones in the present high-temperature true triaxial test.β=0°,β=30°,ω=0°,and ω=90°are also used to comprehensively study the influence of the principal stress orientation.
Three representative temperatures of 25°C,100°C,and 200°C are selected to investigate the effect of temperature on the anisotropic mechanical properties of the gneiss granite.The temperature of the hot spring in the vicinity of the studied tunnel has reached 92°C.Thus,one can roughly evaluate the influence of the hot spring on the mechanical behavior of the surrounding rocks based on the test results obtained at 100°C.The studied tunnel is located in the Lhasa-Gangdis plate,where heat flow values are around 100 mW/m2.The Lhasa-Gangdis plate contains abundant geothermal resources,and the predicted temperature of the thermal reservoir is about 150-200°C.Therefore,the test data obtained at 200°C can provide a basis for the safety assessment of tunnels under extreme conditions and support geothermal energy extraction in adjacent areas.
The high-temperature true triaxial compression test mainly includes four loading stages,i.e.hydrostatic stress loading,temperature loading,biaxial stress loading,and deviatoric stress loading.The method for the stress loading is shown in Fig.5.In this study,both hydrostatic stress and biaxial stress are loaded by stress control mode at rates of 0.2 MPa/s and 0.5 MPa/s,respectively.To obtain the post-peak mechanical properties of gneiss under hightemperature true triaxial compression,the deviatoric stress is loaded at a constant stress rate of 0.5 MPa/s when it is smaller than the damage stress σcd,and a constant displacement rate of 0.006 mm/min in the ε3direction when it reaches σcd.
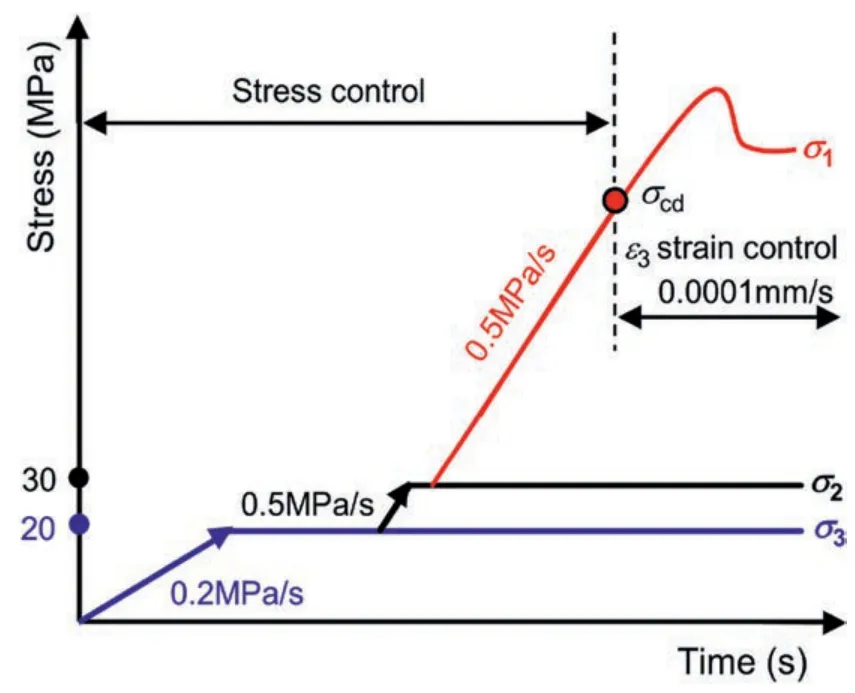
Fig.5.Applied stress path during the high temperature true triaxial compression testing.
2.5.Experimental procedure
Each high-temperature true triaxial compression test is mainly carried out in the following steps:
(1) Calibrate the deformation sensor (LVDT) and temperature sensor.
(2) Install the sample to ensure that the axis of the specimen is parallel to the loading direction.
(3) Load the sample in the hydrostatic state to a given level(20 MPa,e.g.) at a constant rate of 0.2 MPa/s.
(4) After the deformation is stabilized in the hydrostatic stress state,the temperature is applied to a selected value and held for 2 h (Gao et al.,2022;Liu et al.,2023).
(5) Apply the biaxial stress.The σ3is maintained at 20 MPa while σ1and σ2are simultaneously loaded to 30 MPa at a constant rate of 0.5 MPa/s.
(6) Apply the deviatoric stress.The σ1is monotonically loaded at an initial constant rate of 0.5 MPa/s with σ2and σ3are constant.When the deviatoric stress increases up to the damage stress σcd,σ1is loaded at a fixed strain rate of ε3=0.006 mm/min until the test is terminated(Wang et al.,2022a).
3.Experimental results
3.1.Stress and strain
A series of true triaxial compression tests was conducted on the gneiss granite samples according to the experimental program(Table 1).Fig.6 shows the stress-strain curves obtained under different maximum principal stress directions (β=0°,β=30°,β=60°)when the intermediate principal stress direction is 45°and the temperature is 25°C.Fig.7 presents the stress-strain curves obtained under different intermediate principal stress directions(ω=0°,ω=45°,ω=90°) when the maximum principal stress direction is 60°and the temperature is 25°C.Fig.8 gives the stressstrain curves obtained under different temperatures (T=25°C,T=100°C,T=200°C) when the maximum principal stress direction is 0°and the intermediate principal stress direction is 45°.To study the effect of temperature on inherent anisotropy,hightemperature true triaxial compression tests were also conducted at different conditions(β=30°,ω=45°;and β=60°,ω=90°),and the corresponding stress-strain curves are shown in Figs.9 and 10.Note that all tests were realized at σ2=30 MPa and σ3=20 MPa,respectively.

Fig.6.Stress-strain outputs of true triaxial compression tests carried out with three different σ1 directions at ω=45°and T=25 °C:(a)ε1 vs σ1-σ3,ε2 vs σ1-σ3,ε3 vs σ1-σ3;and(b)εv vs σ1-σ3.

Fig.7.Stress-strain outputs of true triaxial compression tests carried out with three different σ2 directions at β=45°and T=25 °C:(a)ε1 vs σ1-σ3,ε2 vs σ1-σ3,ε3 vs σ1-σ3;and(b)εv vs σ1-σ3.

Fig.8.Stress-strain outputs of true triaxial compression tests carried out with three different temperatures at β=0° and ω=45°:(a)ε1 vs σ1-σ3,ε2 vs σ1-σ3,ε3 vs σ1-σ3;and(b)εv vs σ1-σ3.

Fig.9.Stress-strain outputs of true triaxial compression tests carried out with three different temperatures at β=30° and ω=45°:(a)ε1 vs σ1-σ3,ε2 vs σ1-σ3,ε3 vs σ1-σ3;and(b)εv vs σ1-σ3.
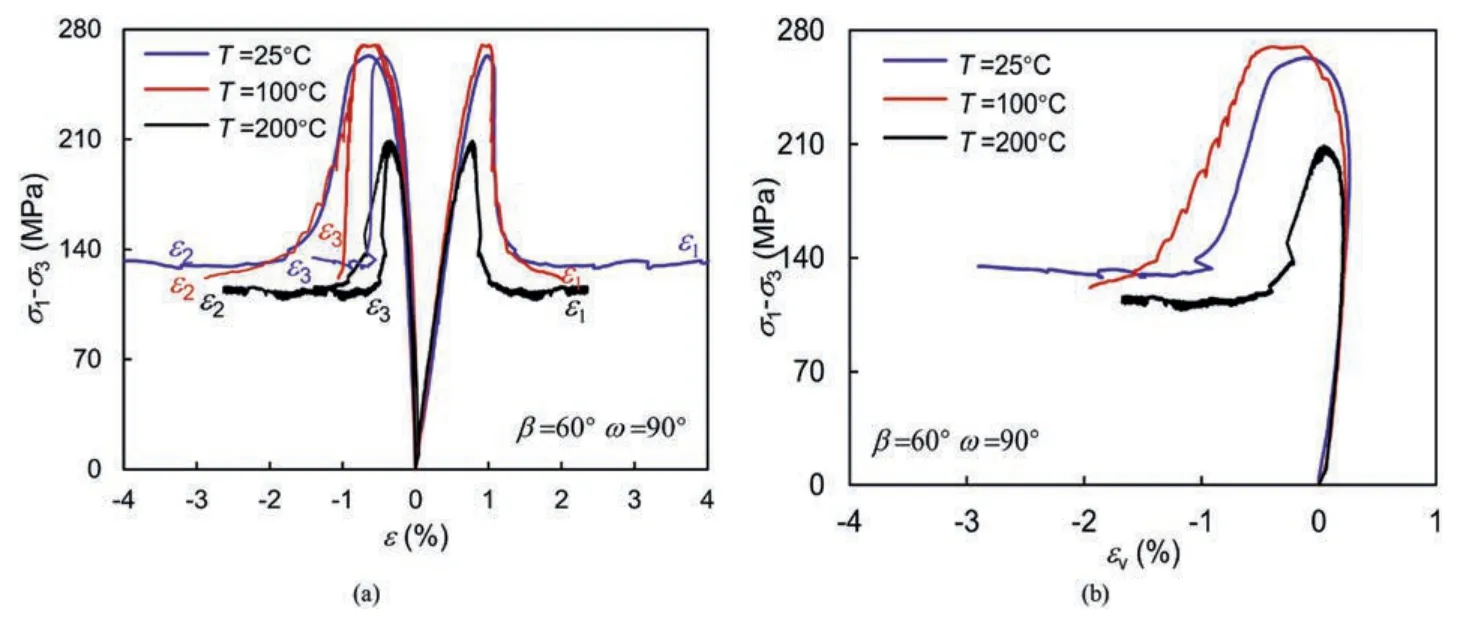
Fig.10.Stress-strain outputs of true triaxial compression tests carried out with three different temperatures at β=60° and ω=90°:(a)ε1 vs σ1-σ3,ε2 vs σ1-σ3,ε3 vs σ1-σ3;and(b)εv vs σ1-σ3.
The relationship between the strain and the deviatoric stress in three principal strain directions,and the relationship between the volumetric strain and the deviatoric stress are shown in Figs.6-10.In this study,σ1-σ3denotes the deviatoric,ε1,ε2,ε3are respectively the strains in the directions of σ1,σ2and σ3.εvrepresents the volumetric strain and it is calculated by εv=ε1+ε2+ε3.
From Figs.6-10,one can find that the stress and strain at failure vary with loading orientation and temperature,confirming that the gneiss granite in the present study exhibits an anisotropic structure,and its strength and deformation behavior are sensitive to changes in temperature.Additionally,as shown in Figs.7a and 10,in the post-peak stage,the value of ε2is greater than ε3when the intermediate principal stress is perpendicular to the bedding plane.In contrast,the value of ε2is smaller than ε3when the intermediate principal stress is parallel to the bedding plane.These phenomena indicate that the deformation behavior of the gneiss granite in true triaxial compression is significantly influenced by the direction of the intermediate principal stress.
3.2.Strength and deformation parameters
The effects of temperature and principal stress orientation on the anisotropic mechanical behavior of gneiss granite under true triaxial compression can be well evaluated by the changes in strength and deformation parameters.The parameters obtained from the stress and strain curves shown in Figs.6-10 are the peak stress σp,crack damage stress σcd,crack initiation stress σci,residual stress σr,strains at peak stress εpeak,elastic modulusE,and Poisson’s ratio υ.The method for the determination of strength and deformation parameters is as follows.
The peak stress is the maximum value of the deviatoric stress on the stress-strain curve.The crack damage stress corresponds to the reversal point of volumetric strain and deviatoric stress curves.In this study,crack initiation stress σciis identified by using a lateral strain model (Nicksiar and Martin,2012).The strains at the peak stress are the peak strain εpeak.The elastic modulusE,Poisson’s ratio υ12,and Poisson’s ratio υ13are calculated bywhere dε1,dε2,and dε3are the strain increments in the direction of σ1,σ2and σ3respectively.
The strength and deformation parameters of the gneiss granite under different principal stress directions and different temperatures are given in Table 2.Based on these parameters,we analyze the anisotropic mechanical behavior of the gneiss granite under high-temperature true triaxial compression in the next section.
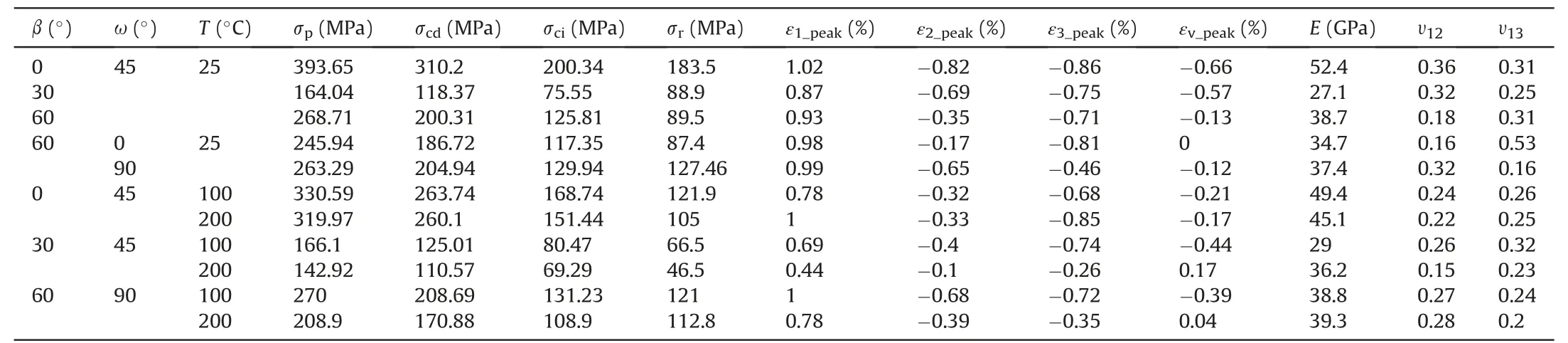
Table 2 Strength and deformation parameters obtained from high-temperature true triaxial compression tests in gneiss granite.
4.Analysis and discussion
4.1.Strength anisotropy
The value of σp,σcd,σciand σrare good indicators quantifying the rock’s strength characteristics.The effect of the principal stress direction on σp,σcd,σciand σrof the gneiss granite under true triaxial compression is presented in Fig.11.For a given temperature of 25°C and a constant ω of 45°,the minimum strength is observed at β=30°,and the strength measured at β=0°is higher than that obtained at β=60°.These results are consistent with those obtained in uniaxial and triaxial compression tests for typical anisotropic rocks (Nasseri et al.,2003;Cho et al.,2012).

Fig.11.Strength parameters of the gneiss granite versus principal stress directions under true triaxial compression:(a)σp,σcd,σci,and σr under different β;and(b)σp,σcd,σci,and σr under different ω.
Different from uniaxial compression and triaxial compression,a true triaxial compression test can study the influence of intermediate principal stress loading orientation ω on the mechanical properties of rocks with inherent anisotropy.The change of σp,σcd,σciand σrof gneiss granite with intermediate principal stress direction,is illustrated in Fig.11b.As ω increases,the values of σp,σcd,σciand σrtend to increase.Notably,σp,σcd,σciand σrmeasured at ω=90°are higher than those obtained at ω=0°.Therefore,a large ω can enhance the strength behavior of gneiss granite both in the pre-peak and post-peak stages.
Experimental values of σp,σcd,σciand σrin high-temperature true triaxial compression tests are depicted in Fig.12.In Fig.12ac,σp,σcdand σcitend to respond differently in increasing the temperature under different principal loading directions.As the temperature increases from 25°C to 200°C,the σp,σcdand σcidecrease continuously at (β=0°,ω=45°),while increase slightly and then decrease at (β=30°,ω=45°) and (β=60°,ω=90°).These results indicate that,in the pre-peak stage,inherent anisotropy can affect the thermal effects of the strength behaviors of granite gneiss.Previous studies have found that the thermal expansion coefficient of anisotropic rocks such as such as slate(Ding et al.,2020) and layered sandstone (Zhou et al.,2016a) can exhibit strong anisotropy.Moreover,it is widely believed that the thermal effects on the mechanical properties of rocks are closely related to the thermal expansion (Zhou et al.,2022).This means that if the thermal expansion of anisotropic rocks is anisotropic,their thermomechanical behavior can be anisotropic.These results further support our findings that,in the pre-peak stage,the thermal effects of the strength behavior of granite gneiss samples vary with the principal stress loading direction.

Fig.12.Strength parameters of gneiss granite as a function of temperature at different principal stress directions:(a)Peak stress;(b)Crack initiation stress;(c)Crack damage stress;and (d) Residual stress.
In the post-peak stage,as shown in Fig.12d,σrcontinues to decrease as temperature increases from 25°C to 200°C for different loading orientations.The variation of σrof gneiss granite under high temperature true triaxial compression can be roughly attributed to the following two mechanisms.The first is that the σris thought to be governed by frictional behavior.It has been found that a high temperature can induce a decrease in the friction coefficient of quartz and feldspar (Masuda et al.,2019),which drives the thermal degradation of the strength of rocks that contain a larger amount of quartz or feldspar.The gneiss granite samples used in this study contained up to 50% feldspar and 10% quartz(Fig.3).Thus,for a given loading orientation and a constant stresslevel,it is reasonable that the σrdecreases continuously with increasing temperature.The second mechanism involves changes in the rock structure.In the residual stage,the original complete structure of the rock is broken.Hence,σrcontinues to decrease as temperature increases from 25°C to 200°C for different loading orientations.
4.2.Stress and strain
The deformation characteristics of anisotropic rocks under true triaxial compression are important for theoretical analysis and engineering practice.The elastic modulus and Poisson’s ratio under different principal stress orientations are illustrated in Fig.13.One can find in Fig.13a that the maximum and minimum values of elastic modulus appear respectively at β=0°and β=30°.The Poisson’s ratios υ12and υ13at β=0°are higher than those at β=45°and β=60°.Fig.13b shows theE,υ12and υ13measured at different intermediate principal stress orientations (ω=0°;ω=45°;ω=90°).The value ofEis 34.7 GPa at ω=0°,and when ω=45°and ω=90°,values ofEare 38.7 GPa and 37.4G Pa,respectively.Hence,the value ofEincreased with increasing intermediate principal stress orientations ω.For υ12and υ13,the values of υ12increase continuously as the ω increases.On the contrary,the values of υ13decrease continuously as the ω increases (Fig.13b).

Fig.13.Deformation parameters of the gneiss granite versus principal stress directions under true triaxial compression:(a)E,υ12,and υ13 under different β;and(b)E,υ12,and υ13 under different ω.
In the linear elastic stage,the loading rate of the deviatoric stress in all experiments is 0.5 MPa/s.According to the definitions ofE,υ12and υ13given by Eqs.(1)-(3),for a given deviatoric stress increment Δq=0.5 MPa/s,the smaller theE,the smaller the deformation in the direction of σ1.Moreover,when the deviatoric stress increment and the deformation in σ1direction are given,the smaller the υ12and υ13,the smaller the deformation in σ2and σ3directions.
Based on the above analysis,it is confirmed that the principal stress directions significantly affect the linear elastic deformation behavior of gneiss granite under true triaxial compression.The increase of ω strengthens the deformability in the σ1and σ2directions while weakening that in the σ3direction.
The effect of temperature on the deformation behavior of gneiss granite under true triaxial compression are illustrated in Fig.14.As shown in Fig.14a,the changes ofEare not only related to the temperature level,but also to the principal stress orientation.The values ofEdecrease with increasing temperature at (β=0°,ω=45°),while at (β=30°,ω=45°) and (β=60°,ω=90°),the response ofEto a temperature increase is opposite to that obtained at(β=0°,ω=45°).The thermal effect of υ13also exhibits loading orientation dependence(Fig.14c).υ13continuously decreases with increasing temperature at(β=0°,ω=45°).However,at the other two principal stress orientation combinations(β=30°,ω=45°and β=60°,ω=90°),υ13first increases and then decreases as the temperature increases from 25°C to 200°C.υ12decreases continuously with increasing temperature,as shown in Fig.14b.
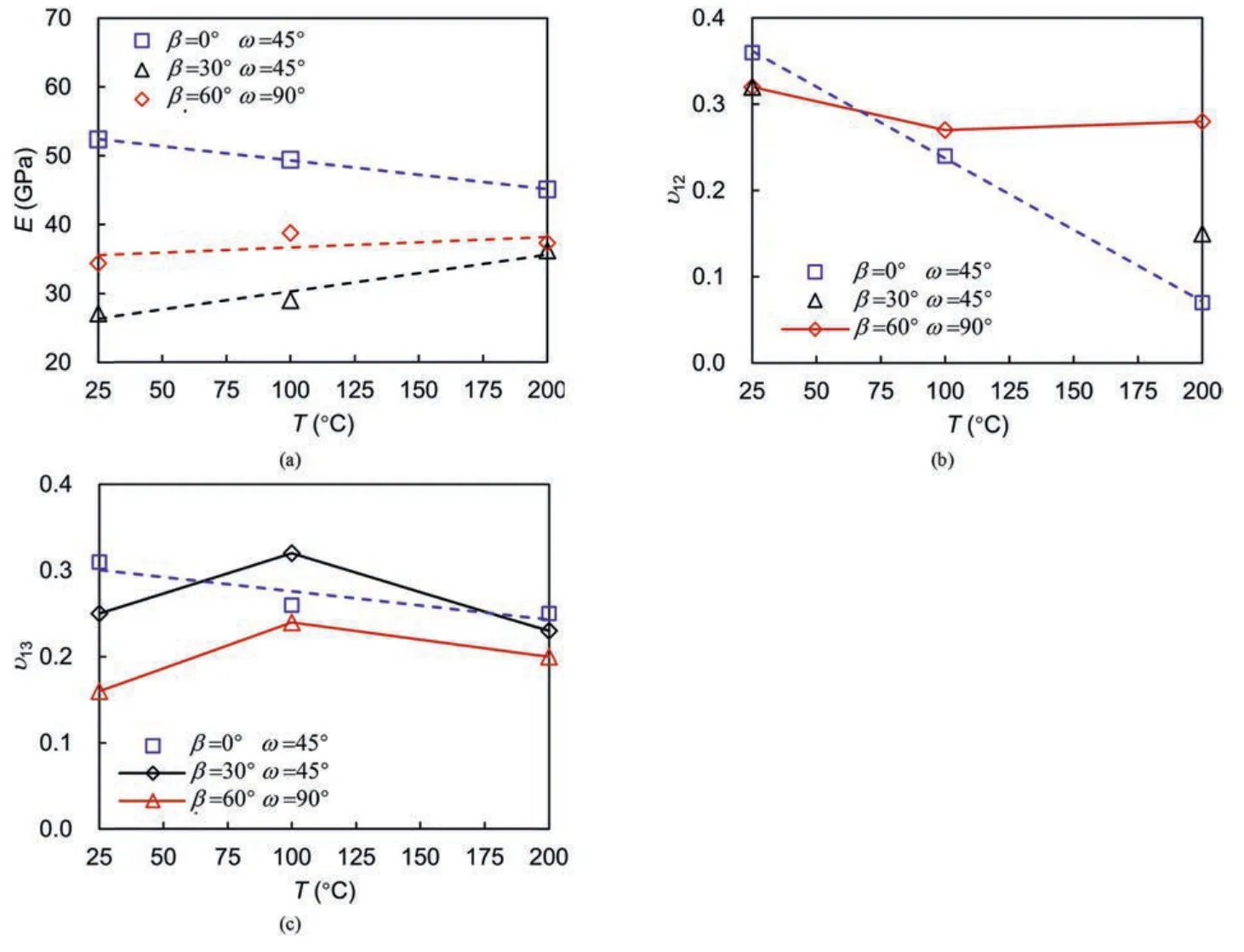
Fig.14.Deformation parameters of gneiss granite as a function of temperature at different principal stress directions:(a)Elastic modulus E;(b)Poisson’s ratio υ12;and(c)Poisson’s ratio υ13.
Therefore,under true triaxial compression,the principal stress orientation and temperature play a key role in the deformation behavior of the gneiss granite.Importantly,the influence of temperature on the deformation differs when the principal stress orientations are different.
4.3.Stress-induced anisotropy change by temperature
The stress-induced anisotropy is defined as the anisotropy of the physical-mechanical properties of rock due to non-hydrostatic stress (Wu and Hudson,1991;Bruno,1994;Feng et al.,2019b).Under a true triaxial compression stress state,the difference between deformation in the σ2direction and deformation in the σ3direction is a common illustration of the stress-induced deformation anisotropy.To understand the stress-induced deformation anisotropy of gneiss granite under high-temperature true triaxial compress,the stress-induced deformation anisotropy coefficients are proposed in Eqs.(4) and (5):
Fig.15 shows the variation of stress-induced deformation anisotropy with temperature at different loading stages.One can find that for a given temperature,ζ and η obtained at β=60°,ω=90°are significantly higher than those obtained at β=0°,ω=45°and β=30°,ω=45°.As shown in Fig.18,at β=60°,ω=90°,the macroscopic fracture only develops along the direction parallel to σ3.However,at β=0°,ω=45°and β=30°,ω=45°,the macroscopic fracture develops along both the σ2and the σ3directions.Therefore,it is logical the deformation difference between the σ2direction and the σ3direction at β=60°,ω=90°are higher than that at β=0°,ω=45°and β=30°,ω=45°.These results indicate that ζ and η can quantify the stress-induced anisotropic deformation under true triaxial compression.
One can also see in Fig.15 that both ζ and η decrease with increasing temperature at β=0°,ω=45°and β=30°,ω=45°.Moreover,when β=60°,ω=90°,ζ and η obtained at high temperatures (100°C and 200°C) are smaller than those obtained at room temperature(25°C).Therefore,it can be concluded that high temperatures weaken the stress-induced deformation anisotropy under true triaxial compression.
4.4.Inherent anisotropy change by temperature
The strength and deformation of the studied gneiss granite exhibit obvious anisotropy in high-temperature true triaxial compression.In uniaxial and triaxial compression,strength anisotropy degree and elastic modulus anisotropy degree are widely used to evaluate the inherent anisotropy (Nasseri et al.,2003).However,in true triaxial compression,the complex combination of principal stress directions makes it difficult to determine these parameters.Therefore,this study uses the strength ratio φ and elastic modulus ratio ψ to quantify the inherent anisotropy of gneiss granite:
The values of φ and ψ under different principal stress directions,as a function of temperature,are plotted in Fig.16.For a given temperature,the values of φ and ψ at β=0°,ω=45°are different from those at β=60°,ω=90°,indicating the inherent anisotropy of the gneiss granite.For a given principal stress direction,one can observe that the values of φ at high temperatures of 100°C and 200°C are generally lower than those at room temperature of 25°C.As the temperature increases from 25°C to 200°C,the value of ψ decreases continuously (Fig.16b).These results imply that high temperature weakens the inherent anisotropy of gneiss granite.

Fig.16.Change of inherent anisotropy with temperature at different principal stress directions: (a) Strength ratio vs T;and (b) Elastic modulus ratio vs T.
4.5.Mechanism of the effect of loading orientation and temperature
The failure behavior of anisotropic rocks is closely related to their strength and deformation.Therefore,this section discusses the mechanism of how loading orientation and temperature affect the mechanical properties of gneiss granite from the perspective of multi-scale failure behavior.It is well known that single diagonal shear failure with the strike parallel to the σ3direction is the most common failure of rocks under true triaxial compression(Fig.17a).In the presence of bedding planes,however,anisotropic rocks have another typical failure under true triaxial compression,single diagonal shear failure with the strike parallel to the σ2direction(Fig.17b).Such a failure has been observed in the true triaxial compression tests of schist (Mogi,2006),gneiss (Liu et al.,2020),and layered limestone (Zhou et al.,2016b).The schema of the typical failures of the anisotropic rocks in true triaxial compression tests and the definition of the failure surfaces and failure angle is given in Fig.17.

Fig.17.Schema of the typical failure of the anisotropic rocks in true triaxial compression:(a)Diagonal shear failure with the strike parallel to the σ2 direction;and(b) Diagonal shear failure with the strike parallel to the σ3 direction.
The post-failure of the gneiss granite in the true compression tests under different loading orientations and temperatures are shown in Fig.18a-k.As shown in Fig.18,three failure patterns were observed on the tested samples:mixed shear failure(Fig.18a,b,c,f,g,h,k),diagonal shear failure with the strike parallel to the σ2direction(Fig.18e),and diagonal shear failure with the strike parallel to the σ3direction (Fig.18d,i,j).In Fig.18,dashed lines mark the outline of the sample’s failure surface.The color of the dashed lines corresponds to the specific failure pattern.Among them,yellow represents mixed shear failure.Blue and dark pink respectively represent diagonal shear failure with the strike parallel to the σ3and σ2directions.The white dashed line represents the localized cracks.

Fig.18.Failure pattern and cracking feature of gneiss granite in thermal-mechanical coupled true triaxial compression test: (a) T=25 °C,β=0°,ω=45°;(b) T=25 °C,β=30°,ω=45°;(c)T=25 °C,β=60°,ω=45°;(d)T=25 °C,β=60°,ω=90°;(e)T=25 °C,β=60°,ω=0°;(f)T=100 °C,β=0°,ω=45°;(g)T=100 °C,β=30°,ω=45°;(h)T=200 °C,β=30°,ω=45°;(i) T=100 °C,β=60°,ω=90°;(j) T=200 °C,β=60°,ω=90°;and (k) T=200 °C,β=0°,ω=45°.
The failure behavior of the gneiss granite under true triaxial compression is greatly dependent on the loading orientation,as shown in Fig.18.When σ2is inclined at an angle of 45°with respect to the bedding plane,the samples experience mixed shear failure under different temperatures and σ1loading directions(Fig.18a,b,c,f,g,h,k).In addition,at β=0°,ω=45°,the mixed shear failure of gneiss granite is dominated by matrix shear,and the failure surface is partially along the bedding plane (Fig.18a,f,k).However,at β=30°,ω=45°,the mixed shear failure of the samples is dominated by bedding shear,and the failure angle values are close to the inclination angle of the bedding (Fig.18b,c,g,h).Therefore,if the strength of the bedding planes is lower than that of the matrix,then it is reasonable for gneiss granite to reach a minimum strength at β=30°(Fig.11a).
The failure behavior depicted in Fig.18 also indicates that,for a given σ1loading direction of β=60°,the samples experience diagonal shear failure at both ω=0°and ω=90°.Specifically,the strike of the failure surface is parallel to σ2when ω=0°(Fig.18e),and parallel to σ3when ω=90°(Fig.18d,i,j).These results confirm the influence of σ2direction on the failure of the gneiss granite.Meanwhile,the change in the failure pattern well explains the observed variation of strength and deformation with σ2direction in Figs.11b and 13b.
In the case of diagonal shear failure,the force that acts on the sample can be resolved into components normal and parallel to the failure plane.The normal stress component directly confines the propagation of the macro cracks,thereby controlling the strength and deformation behavior of the rocks (Mogi,1967).In Fig.18,the sample has the same failure angle at ω=0°and ω=90°.Therefore,given σ2=30 MPa and σ3=20 MPa,it can be inferred that the normal stress component at ω=90°is higher than atw=0°.This results in gneiss granite having a higher strength and elastic modulus at ω=90°than at ω=0°(Fig.11b).Based on the failure pattern(Fig.18),the main crack propagates perpendicular to the σ3direction at ω=0°,and perpendicular to the σ2direction at ω=90°.This crack propagation pattern causes the sample to laterally dilate mainly along the σ3direction at ω=0°,and mainly along the σ2direction at ω=90°.Consequently,the deformation in the σ2direction is greater at ω=90°than at ω=0°,which explains the increase in υ12with increasing ω and the decrease in υ13with increasing ω (Fig.13b).
On the other hand,at a given stress level and loading direction,there are no considerable differences in the shear plane between the gneiss granite samples tested at 25°C,100°C,and 200°C.Nonetheless,we observed many localized shear and tensile cracks around the shear plane for the sample that failed at 200°C,as depicted in Fig.18k.These findings are in good agreement with our earlier observations from high-temperature triaxial compression tests on granite (Liu et al.,2023) and claystone (Liu et al.,2019b).Hence,it appears that localized cracks may serve as an indicator of the thermal effects of rock.The localization of cracks also proves that for anisotropic gneiss granite,their failure is affected by the coupling of stress direction and temperature.Among them,the principal stress direction dominates the macroscopic failure pattern in the temperature range from room temperature to 200°C.
To further characterize the thermal effect of the failure behavior of gneiss granite in the thermal-mechanical coupled true triaxial compression test and to reveal the thermal degradation mechanism of the strength behavior,we analyze the representative zones on the failure surface of the samples that failed under different temperatures by the ultra-depth three-dimensional microscope and scanning electron microscope.Fig.19 shows the multiscale features of the failure surface of gneiss granite that failed at temperatures of 25°C,100°C,and 200°C when the loading direction are β=0°and ω=45°.

Fig.19.Multiscale features of the failure surface of gneiss granite in thermal-mechanical coupled true triaxial compression test.
Fig.19a-c shows the macroscopic morphology of the failure surface,indicating that at a temperature of 200°C,the failure surface of the gneiss granite is covered by a large amount of rock powder.Additionally,obvious friction scratches were found on the failure surface of the specimens failed at each temperature(Fig.19d-f).This suggests that the rock powders are formed during shear sliding.Therefore,friction plays a critical role in the deformation and failure of gneiss granite under thermal-mechanical coupled true triaxial compression.From Fig.19a-f,the failure surface formed at 100°C and 200°C is smoother than that formed at 25°C.The amount of rock powder at 200°C is significantly higher than that at 25°C.Our previous high-temperature triaxial compression tests on granite have revealed that these variations in the failure surface indicate that the high temperature weakens the friction between the failure surfaces(Zhou et al.,2022).Therefore,the change in friction is closely linked to the thermal effect of the strength and deformation of gneiss granite.
Fig.19g,h and i depicts the microscopic morphology of the failure surface of the gneiss granite that failed at 25°C,100°C,and 200°C,respectively.The presence of river lines and shear steps on the grains indicates that,at the microscopic scale,the failure of the samples under thermal-mechanical true triaxial compression is primarily due to shear fracture and cleavage fracture.At 25°C and 100°C,most of the grains remain intact,with clear grain boundaries and noticeable transgranular and intergranular cracks.It is worth noting that the damage of the grains appears slightly more severe at 100°C than that at 25°C,manifested as the crushing of edges in a small number of grains.At 200°C,the majority of grain edges,and even some grains,are crushed,and the boundaries of most grains cannot be distinguished.These findings indicate that the rock powder on the failure surface is essentially crushed rock grains.Thus,the high temperature of 200°C appears to alter the strength of rock grains and the cementation strength between rock grains,further impacting the microscopic failure mechanism of rock grains.
Hence,the thermal degradation mechanism of the strength and deformation of gneiss granite in thermo-mechanical coupled true triaxial compression can be explained as follows.At the macroscopic scale,weakening of friction between the shear failure surfaces is one of the primary factors that can cause a reduction in the rock’s shear resistance.At the microscopic scale,changes in grain failure mechanisms also contribute to thermal degradation.
5.Failure pattern identification
The identification of failure patterns in rock mass under in situ stress conditions is crucial for assessing the stability of deep underground engineering.Many studies (Mogi,2006;Zhou et al.,2016b;Liu et al.,2020) have revealed that anisotropic rocks typically exhibit three types of failure patterns under true triaxial compression:Type A-mixed shear failure(Fig.18a,b,c,f,g,h,k);Type B -diagonal shear with the strike parallel to the σ2direction(Fig.18e);and Type C-diagonal shear with the strike parallel to the σ3direction (Fig.18d,i,j).This section proposes a method to identify the unusual failure pattern of Type C.
The failure of rocks under true triaxial compressive stress depends on the difference in the deformation in intermediate principal stress and the minimum principal stress directions.Hence,the change in deformation difference with deviatoric stress is the key to identifying failure modes.In view of this,the deformation ratio,ξ is proposed:
whereD2andD3are the deformation in the direction of σ2and σ3,respectively.The value of ξ quantities the difference in the deformation in the direction of σ2and σ3.The positive value ofD2indicates compression,whereas the negative value ofD3refers to compression.
Fig.20a-k illustrates the evolution of ξ with deviatoric stress for gneiss granite specimens with different failure patterns in thermomechanical-coupled true triaxial experiments.For the samples undergoing Type C failure(Fig.20a-c),it can be observed that during the post-peak stage,the value of ξ is greater than or equal to one and increases with the decrease in deviatoric stress.Thus,we have:
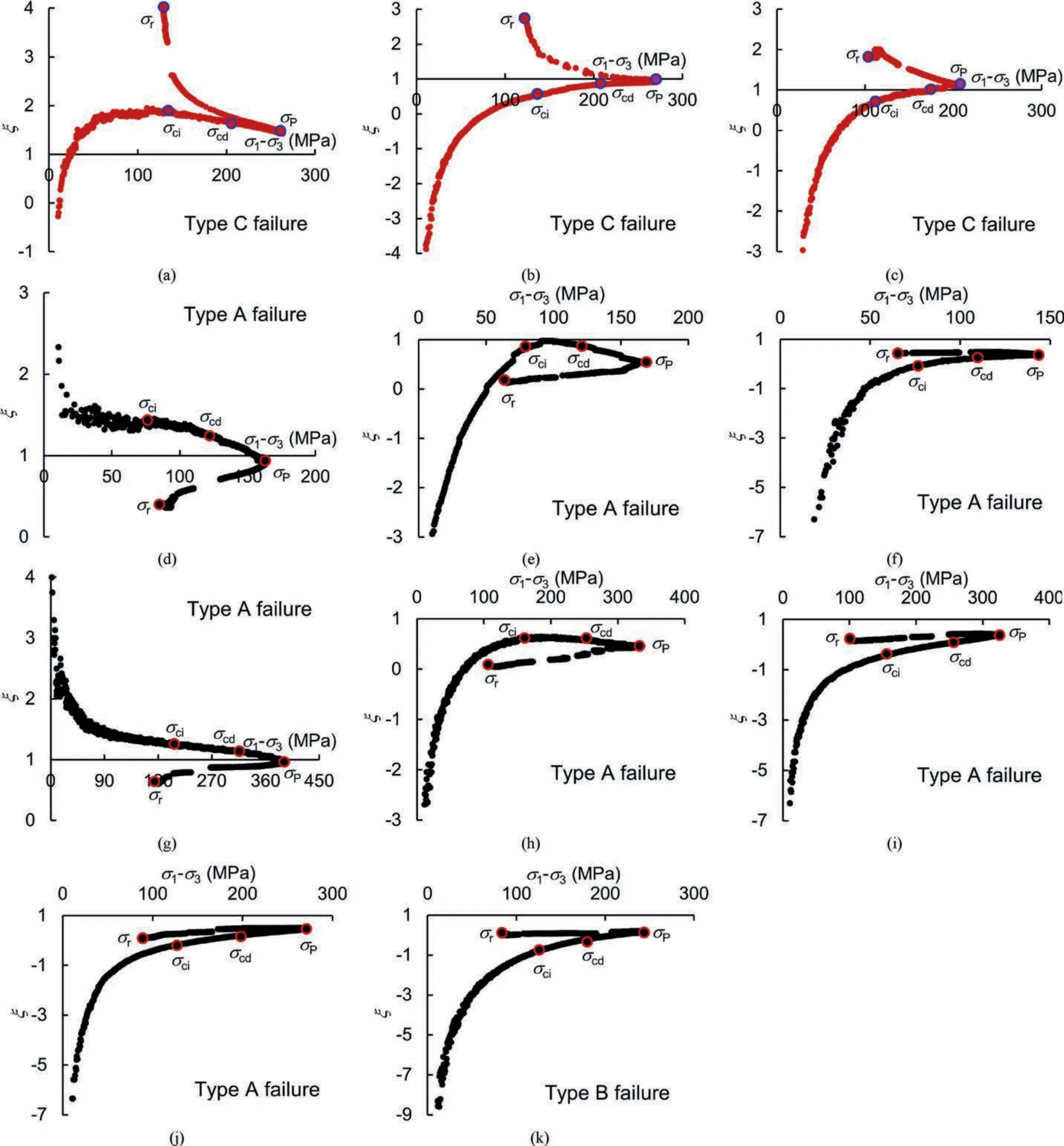
Fig.20.Differences in deformation ratio under different failure patterns in thermal-mechanical coupled true triaxial compression:(a) T=25 °C,β=60°,ω=90°;(b) T=100 °C,β=60°,ω=90°;(c)T=200 °C,β=60°,ω=90°;(d)T=25 °C,β=30°,ω=45°;(e)T=100 °C,β=30°,ω=45°;(f)T=200 °C,β=30°,ω=45°;(g)T=25 °C,β=0°,ω=45°;(h)T=100 °C,β=0°,ω=45°;(i) T=200 °C,β=0°,ω=45°;(j) T=25 °C,β=60°,ω=45°;and (k) T=25 °C,β=60°,ω=0°.
where Δξ and Δqare the increment of ξ and deviatoric stressq.q=σ1-σ3.
For the specimens undergoing Type A failure (Fig.20d-j) and Type B failure (Fig.20k),one can find that during the post-peak stage,the value of ξ is less than one and decreases or keep constant as the deviatoric stress decreases.These results can be expressed as follows:
From Eqs.(10)-(12),it is concluded that if the variation of ξ with deviatoric stress satisfies both Eqs.(9) and (10),then it indicates that the specimen experienced Type C failure under true triaxial compression.
Based on Fig.20,the evolution of ξ with the deviatoric stress during the pre-peak phase is analyzed and compared for the gneiss granite that underwent different failure patterns.We found that among the three types of failure patterns observed,the following two characteristics of ξ appear together only for the samples that underwent Type C failure.The first one is that ξ increases as the deviatoric stress increase when the deviatoric stress is smaller than the crack initiation stress.The second one is that the ξ is greater than or equal to one during the unstable crack propagation stage.Therefore,one can identify and predict the Type C failure by:
6.Conclusions
The anisotropic mechanical behaviors of gneiss granite were investigated by several groups of high-temperature true triaxial compression tests.Effects of temperature and principal stress direction on strength,deformation,and failure were studied.The thermal degradation mechanism of strength was discussed in terms of the failure pattern change.The method for the quantitative identification of the failure patterns was proposed.Based on the obtained experimental results,the main conclusions can be drawn:
(1) The principal stress direction with respect to the bedding plane plays an important role in controlling the strength and deformation of the gneiss granite in true triaxial compression.The peak stress,crack damage stress,crack initiation stress,residual strength,and elastic modulus are greater at ω=90°than at ω=0°.
(2) The thermal effects of the strength and deformation of anisotropic gneiss granite depend on the temperature magnitude and principal stress direction.Within the range of 25°C-100°C,the response of strength and deformation to temperature increase varies with the principal stress direction.The high temperature of 200°C leads to an obvious thermal degradation of strength.The residual stress continues to decrease with the increase of temperature in the range of 25°C-200°C.
(3) In thermal-mechanical coupled true triaxial compression test,gneiss granite exhibits stress-induced deformation anisotropy and inherent anisotropy.Increasing the temperature weakens both types of anisotropy.The failure of gneiss granite mainly shows shear sliding of bedding and matrix at the macroscopic scale and shear fracture and cleavage fracture at the microscopic scale.The principal stress direction dominates the macroscopic failure pattern in the temperature range from 25°C to 200°C.The weakening of friction between shear sliding surfaces and the failure mechanism transition of rock grains contribute to the thermal degradation of strength and deformation.
(4) The loading direction of σ2has a significant influence on the failure of the gneiss granite in true triaxial compression test.When σ2is perpendicular to the strike of the bedding,the sample experiences diagonal shear with the shear plane strike parallel to the direction of σ3.In the case of this failure pattern,the ratio(ξ)between the deformations in σ2and σ3direction is characterized as follows.In the post-peak stage,ξ≥1.In the pre-peak stage,ξ increases as the deviatoric stress increases when the deviatoric stress is smaller than the crack initiation stress,and ξ ≥1 in the unstable crack propagation stage.
It is confirmed in the present study that temperature and principal stress direction significantly affect the anisotropic mechanical behavior of gneiss granite under true triaxial compression.It is known that the anisotropic mechanical behavior of rocks is closely related to the degree of inherent anisotropy.To verify the findings of this study and further study the anisotropic mechanical properties of rocks under the high temperature and true triaxial stress coupled conditions,more high-temperature true triaxial compression tests will be conducted on different types of anisotropic rocks in the next step.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work was supported by Natural Science Foundation of China (Grant No.52278333),the Fundamental Research Funds for the Central Universities (Grant No.N2101021).The work is under the framework of the 111 Project (Grant No.B17009) and Sino-Franco Joint Research Laboratory on Multiphysics and Multiscale Rock Mechanics.
List of symbols
σ1Maximum principal stress
σ2Intermediate principal stress
σ3Minimum principal stress
σciCrack initiation stress
σcdCrack damage stress
σpPeak stress
σrResidual stress
εpeakStrain at peak stress
εkStrain in the principal directionk(k=1,2,3)
dεkStrain increment in the principal directionk(k=1,2,3)
εvVolumetric strain
EElastic modulus
υklPoisson’s ratio of the directionkcaused by the stress in the directionl(k,l=1,2,3)
ω The orientation of intermediate principal stress
β The orientation of maximum principal stress
ζ The degree of stress-induced deformation anisotropy at the linear elastic stage
η The degree of stress-induced deformation anisotropy at failure
φ The strength ratio
ψ The elastic modulus ratio
ξ The deformation ratio
Δξ Increment of the deformation ratio
DkDeformation in the principle directionk(k=1,2,3)
qDeviatoric stress
LLength of the sample
WWidth of the sample
HHight of the sample
ρ Density of the sample
TTemperature
 Journal of Rock Mechanics and Geotechnical Engineering2024年3期
Journal of Rock Mechanics and Geotechnical Engineering2024年3期
- Journal of Rock Mechanics and Geotechnical Engineering的其它文章
- Limit load and failure mechanisms of a vertical Hoek-Brown rock slope
- Limit state analysis of rigid retaining structures against seismically induced passive failure in heterogeneous soils
- Bearing capacity of circular footings on multi-layered sand-waste tire shreds reinforced with geogrids
- Experimental investigation on the permeability of gap-graded soil due to horizontal suffusion considering boundary effect
- Damage constitutive model of lunar soil simulant geopolymer under impact loading
- Wetting-drying effect on the strength and microstructure of cementphosphogypsum stabilized soils
