基于并行粒子群算法的电力系统极限负荷预测研究
刘 卓,许 晨,叶 攀,卢 波
(国网湖北省电力有限公司黄石供电公司,湖北 黄石 435000)
0 引 言
随着现代社会的飞速发展,电力系统的负荷预测成为一个关键环节,对于城市电网规划设计具有重要作用。在电力系统的负荷预测过程中,如何提高预测的准确性是当前电力系统研究的重要方向。运用负荷预测能够保证电力系统的稳定运行,防止设备损坏。通过不断集成电力需求,能够准确预测电力系统的极限负荷。在电力系统中,运行方式正在发生深刻变化,导致实际操作存在许多不确定性因素,而可再生能源的输出变化更复杂。预测过程中,针对不同时期的预测需求提供相应的解决方案,能够提高负荷的预测精度。为避免负荷造成大量的经济损失,满足电能供需平衡,需要提升预测准确性来确保电网运行的安全稳定性,以达到节约成本的目的。在电力负荷预测过程中,预测电力的需求量,选择电力系统需要新增的容量,有助于提升电网的供电质量。通过全面掌握负荷发展规律,有利于实时分析数据安全,实现对故障的有效预防,同时需要校验和多级协调负荷预测结果,制订合理的调度计划,完成负荷预测。传统的负荷预测方法难以满足现代电力系统的需求,当电力需求波动时,可能影响电力系统的极限负荷[1]。规律性方面的处理能力不足,会导致预测误差较大,电力系统过载,严重时可能引发电网崩溃,造成大面积停电,使负荷预测结果难以达到预期[2]。本文以电力系统极限负荷预测为研究对象,运用并行粒子群算法,结合实际情况进行实验与分析。
1 电力系统极限负荷预测
1.1 电力系统极限负荷数据预处理
电力负荷根据供电地区的重要程度分成多种类型。在负荷结构中,掌握电力负荷特性是达成电力系统整体调度的前提[3]。根据已知的负荷序列,可预测未来一段时间内的电力负荷值。为减少预测误差,需要建立科学合理的负荷预测模型,选择真实的电力负荷数据,并预处理原始负荷序列数据。预测过程中,原始负荷序列数据中不符合规律的值为异常值。根据电力负荷具有的周期性,处理误差数据的公式为
式中:y为采样时间;d(y)为设定阈值;d(x,y)为不同时刻的负荷值。运用式(1)将差值与阈值进行比较,处理发现的异常值[4]。在消除异常值后,对数据进行归一化处理,经过归一化处理得到的数据为
式中:xmax为最大值;xmin为最小值;x'为计算值。如果数据不在区间内,则需要标准化处理数据,使数据能够按照一定的比例缩放后存放在特定的区间中,即为无量纲数据。通过一系列数据处理后能够补偿电力系统的缺失数据。根据负荷的实际情况选择合适的模型,将信号分解成负荷序列,并运用算法进行优化,将数据重构后带入预测模型。
1.2 并行粒子群算法在模型中的极限负荷预测
根据电力负荷历史数据的变化规律预估未来的负荷需求。在并行预测体系中,根据不同日期的负荷在相同时刻的相似性,建立一天中不同时刻点的预测模型进行单独预测[5]。从历史预测数据出发,结合未来电力负荷的时间与空间分布,安排电力系统的调度运行。具体的并行预测模型体系结构如图1 所示。

图1 并行预测模型体系结构
训练模型时,选择灰色神经网络的输入变量减少预测偏差[6]。将预处理后的数据输入模型中进行训练与反归一化处理,得到预测结果。使用粒子群算法进行预测,通过群体中个体间的相互协作与信息共享得到最优解。设定模型中存在一组粒子,不同粒子表示不同解的维数空间,通过改变粒子的位置得到最优解。在当前时刻,第i个粒子搜索到的最好位置记为pi。通过迭代能够得到当前时刻的最优粒子,粒子的位置更新公式为
式中:t+1 为粒子更新位置;t为初始位置;v为当前速度。为了防止v过大,需要进行约束,约束范围为v∈[-vmax,vmax]。确定随机初始化粒子的位置,并计算不同粒子的适应度函数。对比粒子的适应度值与当前个体的解,并进行位置更新。引入惯性权重w来增加全局与局部的搜索能力,通过调整w进行动态取值。调整公式为
式中:w0为权重初始值;w1为权重最终值;tmax为迭代最大值。通过调整可增强粒子搜索能力[7]。在搜索过程中,比较当前种群的适应度值与最佳适应度值,位置更优则进行替换,直到满足条件后结束。如果预测结果满足预先设定的阈值,则停止,反之则继续寻优。通过并行粒子群算法在模型中预测短期负荷数据,可有效改善算法的收敛问题,提升全局的预测能力。
2 实验测试与分析
2.1 搭建实验环境
实验在Python 2.3.6的Keras 1.2学习框架下进行。实验所用的数据集包含历史负荷数据等,采集数据的频率为30 s/次。训练数据并生成训练集与预测集,经过筛选后将数据作为模型的输入数据,归一化处理数据并输入全连接层,得到最终的预测结果。运用3种方法进行预测,其中本文方法预测的小组为实验组,传统方法预测的小组分为对照A 组和对照B 组。采用独热编码处理日期数据,并设置模型参数,具体设置如表1 所示。

表1 模型参数设置
运用不同预测方法迭代训练模型,并计算所有实验需要的数值。
2.2 结果与分析
针对3 个小组的输出模型,得到1 月30 日—4 月10 日的预测负荷曲线对比图,如图2 所示。
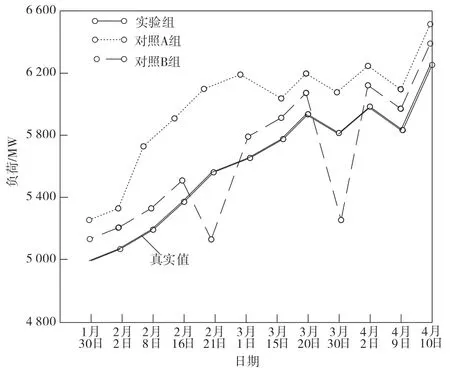
图2 模型预测对比图
由图2 结果可知,2 个对照组的模型预测结果不太理想,对照B 组存在2 个波谷阶段,增大了预测过程的误差,预测结果与真实值存在差异。相比对照组,实验组模型的表现较好,其预测结果与真实值更相符,说明使用本文预测方法能够较好地处理具有时序性特征的问题,使极限负荷预测结果更加准确和理想。
运用本文预测方法计算模型输出评价指标中的平均绝对误差值,计算公式为
式中:m为预测样本个数;(x,y)为样本预测值;G为样本平均值。10 次预测后,得到计算的平均绝对误差结果,判断该模型的拟合效果(规定误差范围为0.00 ~0.40 MW),结果如表2 所示。
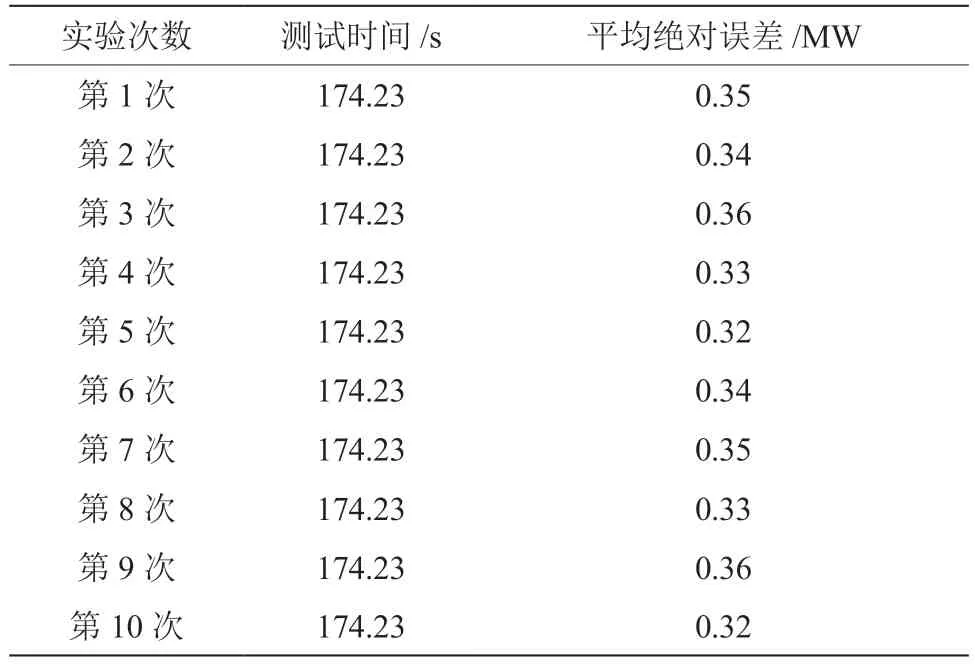
表2 预测平均误差结果
由表2 数据可知,10 次实验后,计算的平均误差结果为0.32 ~0.36 MW,在规定误差范围内,符合预期要求,说明运用本文预测方法能够提升电力系统极限负荷预测的准确性,使整体的预测效果更佳。通过负荷变化特征,可达到对未来负荷的准确预测。
综上所述,运用本文电力系统极限负荷预测方法,当负荷变动频繁时能够提高预测稳定性,提取极限负荷的高维动态特征,使曲线拟合效果分别在不同阶段达到最佳。通过挖掘电力负荷的内在规律,可提升预测精度。
3 结 论
本文探究基于并行粒子群算法的电力系统极限负荷预测,分析短期电力负荷的特性,归类负荷,充分考虑温度和气象等因素,实现对电力系统极限负荷的有效预测。方法中存在不足,如非线性预测能力、不同频率特征分量及负荷数值相似性等问题。在今后的研究中,运用并行粒子群算法进行预测,避免网络在寻优过程中陷入局部最小值。通过使用预测方法得到较好的泛化能力,不断提高预测结果的准确度。

