基于频点影响的频域盲源分离排序算法

张 奇,肖 瑛

(大连民族大学 信息与通信工程学院,辽宁 大连 116605)

盲源分离是在未知源信号和传输信道参数的情况下,从观测信号中恢复源信号的信号处理技术[1]。在实际信号处理中,由于传输延迟、干扰等情况的影响,接收端采集到的信号不是简单的线性混合信号,而是复杂的卷积混合形式。卷积混合信号的盲源分离,在语音识别[2]、图形信号处理[3]、频谱检测[4]、医学信号处理[5]等多个领域都具有实际应用价值。

目前,解决卷积混合盲源分离分时域和频域两种方法。时域方法的主要核心是在时域找到一个分离滤波器[6],它的滤波阶数与混合滤波器阶数相同或更大,当滤波器阶数过大时,时域方法会存在复杂的卷积运算。频域方法是利用短时傅里叶变换(Short-time Fourier transform, STFT)将信号进行时频转换,并利用目前成熟的独立分量分析(Independent Component Analysis, ICA)等[7]算法进行频域盲源分离得到解混信号,因此频域方法在卷积混合形式中扮演着重要角色。频域方法操作简单、易于实现,但ICA算法引入了幅度歧义性和排序歧义性[8],频域方法的准则主要取决于信号频点排序的准确性,故在进行反傅里叶变换之前,必须解决各频点估计信号的歧义性问题,其中排序歧义性问题更为重要。

当前有多种解决排序歧义性问题的方法。Ikram等[9]利用信号间频谱相位信息,估计各频点波达方向角(DOA)来确认源信号,再以此为特征进行独立分量聚类,确定所对应的信号源,这种算法需明确源信号的实际位置和环境,属于半盲算法。Murata等[10]利用频点的幅度相关度排序,依据相邻频点的频谱幅度具有很高的相关性对频点依次排序,但该性能不稳定、鲁棒性差,某一频点排序不准确将影响信号其他频点的准确性。随后薄祥雷等[11]演变出的IF-Murata算法提高了幅度相关性算法的频点相关性,但依然存在着性能不稳定的缺点。

针对以上排序算法的不足,本文提出了基于频点影响的改进频点排序算法。该算法通过权重系数控制分离矩阵的一致性,保持频点之间的相关性,并将得到的分离矩阵作为频点排序的依据;再利用影响因子控制频距和频质对频点排序的影响;最后找到一组相关性最大的频点排列顺序,解决排序歧义性问题,提高算法的稳定性和分离效果。

1 卷积混合的频域盲源分离

假设有N个统计独立的源信号si(t),i=1,2,…,N,卷积混合后传感器接收到M个混合信号xj(t),则线性卷积混合模型可以表示为

(1)

式中:rk为时延参数;hij(k)表示为第i个源信号到第j个传感器的混合滤波器参数;k为FIR滤波器的阶数。当k>1时,为卷积混合模型,其线性卷积形式可以表示为

X(t)=H*S(t) 。

(2)

式中:S(t)=[s1(t),s2(t),…,sN(t)]T为源信号向量;混合信号向量为X(t)=[x1(t),x2(t),…,xM(t)]T;H是M×N的滤波器混合矩阵。

将式(2)两边进行时频变换,得到各个信号的频域混合模型:

X(f,τ)=H(f)S(f,τ) 。

(3)

式中:f为频点;τ为帧序号;S(f,τ)=[s1(f,τ),…,sN(f,τ)]T和X(f,τ)=[x1(f,τ),…,xM(f,τ)]T分别为傅里叶变换后频带f上的第τ帧的源信号和观测信号。

由此可得,频域盲源分离的解混模型为

Y(f,τ)=W(f)X(f,τ) 。

(4)

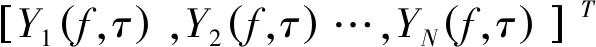
本文通过联合对角化方法[12]对信号各频点进行分离,得到的分离信号需要解决幅度歧义性和排序歧义性问题。对于幅度歧义性可利用分离矩阵归一化[13]得到解决。

(5)

其中Ws(f)为消除幅度歧义性的结果。排序歧义性的消除方法将在第2节进行叙述。

2 改进的幅值相关性排序算法

2.1 幅度相关性排序法

幅度相关性排序的含义是指同一信号相邻频点的相关性要比不同信号相邻频点的相关性要强,利用这一点可实现各频点分离信号的重新排序。相邻频点相关系数定义如下:

(6)

式中:α和β为两个实数向量;E(·)表示求均值;σα和σβ为方差。

Murata等人对于排序信号的频点,以部分领域范围内|f-g|≤L的信号作参考,找到以相邻频点幅度相关度之和的最大一组排列,作为该频点的正确排列方式,目标函数如下:

(7)

经仿真实验得到,Murata算法并不能有效分离复杂信号,主要是因该算法以权重对待各邻近频点所得的幅值相关性,没有考虑频点信号的质量和可靠性,如以质量差的频点作为参考,将影响到整个频点排序的准确性。

当频点的距离逐渐增大时,同源信号不同频点之间的相关性逐渐减小,可能就会出现同一源信号比不同源信号的相关性还要小。在频域中计算频点间的相关性得到如图1。图1(a)表示同源信号频点之间的相关性,图1(b)表示不为同一源信号频点之间的相关性,图1(c)表示同一源信号与不为同一源信号频点之间的差值。可以看到,存在着同一源信号比不同源信号频点间相关性要小的现象,而这些不可靠频点的存在,有可能引发频点排序错误的现象。

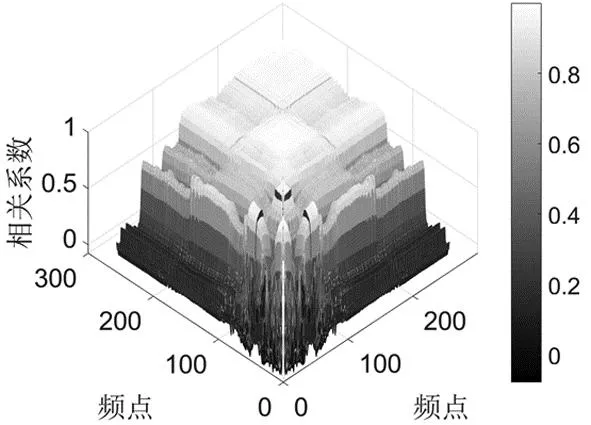
(a) 同源信号频点相关性

2.2 IF-Murata排序法

IF-Murata算法在Murata算法的目标函数上加入了影响频点分离质量和频点距离的影响因子η,根据不同频点观测信号特征设定不同的影响因子,来提高频点排序的正确率。该算法原理是当不同信号之间的相关度大于同一信号的相关度时,频点的距离大,而此时频点间的距离与η成反比;而当分离子信号排序因分离质量差的频点影响越小时,频点间的距离和η成正比。为方便表述,以两路源信号为例,IF-Murata排序法的目标函数可以表示为

(8)

(9)

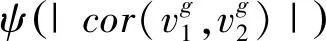
(10)

(11)

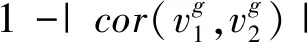
图2 不同δ值的信噪比

综上,可以得到关于影响因子η的排序公式:

(12)

(13)

虽然IF-Murata算法可在一定程度上提高频点排序的正确率,但是该排序法仅通过控制影响因子抑制频点距离过大或分离质量较低的频点,得到的信号分离效果并不理想。

2.3 基于频点影响的排序算法

根据以上阐述可以得到,Murata和IF-Murata的排序算法,都未考虑到频点行列式的连续性[14]对频点排序的重要作用。

在分离矩阵行列式的均值与幅度|det(W(f))|相差较大的情况下,表明行列式的差异大,连续性较差,使频点间的相关性下滑。衡量分离矩阵行列式连续性的差值为

(14)

(15)

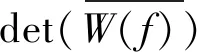
卷积混合信号排序单个相邻频点存在干扰的情况下,将导致信号的顺序歧义性,故应考虑频点的界限范围,范围过长将增大算法的复杂度、分离性能下降,会出现同一源信号相邻频点幅值相关性大于不同源信号的幅值相关性不成立的现象,因此界限范围的表达式为

μ2(g)=|g-f| 。

(16)

其式(16)表示为已排序频点g对未排序频点f的影响。其频点间距越大则μ2(g)-1越小,减小了频距对信号排序的作用,故μ2(g)与权重系数为反比关系。

从以上分析可以得到,已排序频点g对待排序频点f的权重系数为

(17)

式(17)中可以得出需要考虑两个界限范围,分别是分离矩阵行列式的均值界限范围L1和频点排序相邻频点的界限范围L2。

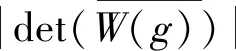
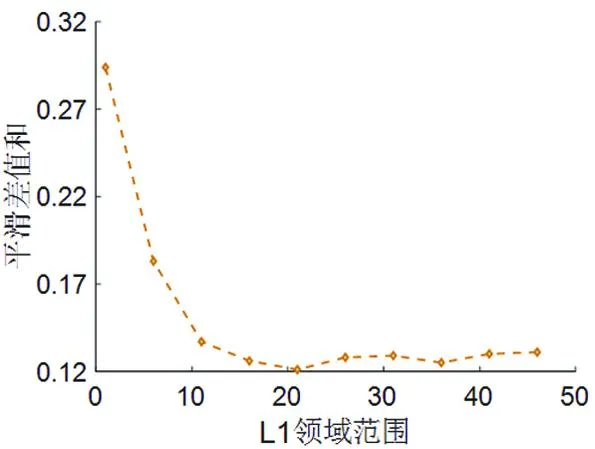
图3 分离矩阵行列式界限范围不同时平滑差值

以两路语音信号为例,利用源信号卷积混合后的混合信号来确定L2的值。设定L1为18时,取L2的不同值,可以得到L2变换值的分离信号信噪比如图4。从图4中可以得到,1≤L2≤9时分离信号信噪比不稳定;L2高于9时分离信号信噪比逐渐平稳。

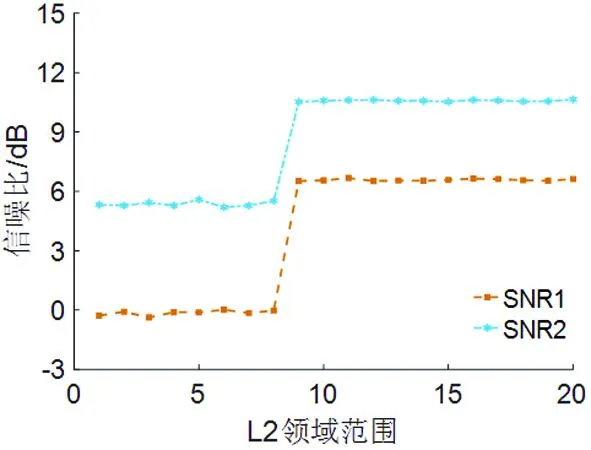
图4 幅度相关性界限范围不同时分离信号信噪比

基于实验结果设定14≤L2≤18,据以上所述,设定权重系数的函数为

(18)

综上,关于权重系数的目标函数为

(19)

经以上分析,本文结合IF-Murata法的影响因子进一步对Murata法改进,得到频点影响的排序算法,实现分离效果更优的卷积混合信号盲源分离,本文改进的算法叫做FR-Murata算法。该算法原理是利用权重系数κ对频点和分离矩阵行列式的限制,再利用影响因子η对频点距离和频点分离质量的控制,提高算法的稳定性和分离信号排序的准确性。

对于多源多路混合信号模型,将式(13)求两信号相关度改为求两两组合相关度的平均值,则本文算法的目标函数为

(20)

(21)

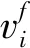
为检验本文频点的排序顺序,采用不同算法对语音信号进行分离,再利用下式(22)判定排序是否正确,若频点排序正确置为0;否则置为1,如图5。Murata算法各频点得到的分离信号M-y(f,τ)与源信号s(f,τ)相关分析的曲线图如图5a,同理可得分离信号FR-y(f,τ)与源信号s(f,τ)的相关分析曲线图5b。

(a)Murata算法频点排序 (b)FR-Murata算法频点排序

cor(y1(f,τ),s1(f,τ))≥cor(y2(f,τ),s1(f,τ)) 。

(22)

对比图5各频点排序的结果可以看出,图5a中一部分的频点相关性较高,而一部分的频点出现了不相关现象,是因频点排序时以错误频点为依据,导致后面频点连续出错。加入影响因子和权重系数的FR-Murata算法是以可靠频点为依据对频点排序,保证了各频点的相似性,因此,该方法排序正确率高,使分离信号有较高的准确性和稳定性。

3 仿真实验与分析

3.1 实验设置

为了检验在室内环境下信号的分离效果,利用模拟工具箱创造一个人为可控的真实室内环境[15]如图6。图6中描述了实验中的房间大小、声源位置和传感器位置。实验使用三路不同的纯净语音,每组语音分别为英文男音、英文女音和中文男音。其中,传感器的采样频率为16 kHz;墙壁的反射系数为0.5;因实验环境存在一定的噪声干扰,故本文未再添加其他噪声。为了简洁,此处只显示出一组传感器得到的室内盲分离结果。

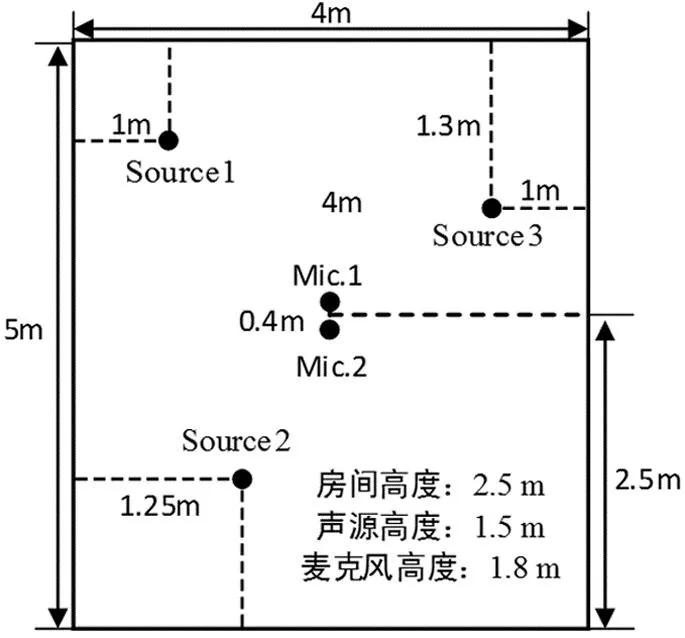
图6 模拟房间分布图

3.2 实验仿真

卷积混合盲源分离的目的在于恢复出输出顺序正确的分离信号。三路源信号时域波形图如图7a;三路混合信号时域波形图如图7b;Murata算法输出的时域信号波形图如图7c; FR-Murata算法输出的时域信号波形图如图7d。从图7c可以看出,Murata算法得到的估计信号有较多的毛刺,并且能明显听到杂音的存在。本文FR-Murata算法得到的时域信号波形图7d相比图7c更贴近源信号,毛刺较少,主观上更易区分。

(a)源信号时域波形

3.3 分离结果评估

由于信号波形不能准确分析分离结果,本文利用相似系数和盲源分离工具箱[16](Blind Source Separation Evaluation,BSS-EVAL)的三个性能指标进行分析。

相似系数的数学表达式为

(23)

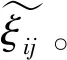
对比Murata算法的计算数据,可以看出FR-Murata算法的相似系数平均提升了约0.1,表明本文算法具有较高的估计精度。

盲源分离工具箱是将分离信号y(t)分解为式(24)所示的几个部分,其中eartif(t)表示由算法产生的人造误差;starget(t)表示正确的估计信号;einterf(t)表示估计信号中不属于源信号但属于观测信号的一部分,这是因其他源信号造成的干扰误差。

y(t)=starget(t)+einterf(t)+eartif(t) 。

(24)

因此可以得到三个性能参数,分别为源信号干扰比(Source-to-Interference Ratio,SIR);系统误差比(Source-to-Artifacts Ratio,SAR);源信号失真比(Source-to-Distortion Ratio,SDR);其数学表达式如下:

(25)

(26)

(27)

为了与FR-Murata算法做比较,同时对传统Murata算法和改进的IF-Murata算法进行性能分析。语音信号卷积混合盲源分离的性能参数对比图如图8。从图8中可以看出,本文FR-Murata算法在SIR,SDR,SAR上相较于其他两种算法均有较大的提升。其中,本文算法在SIR上比Murata算法最高提升约6.1 dB,SDR最高提升约5.8 dB,SAR最高提升约3.9 dB,充分验证了在室内混响环境下本文FR-Murata算法具有较好的分离性能和鲁棒性。

(a) 语音信号SAR性能对比

4 结 语

频域卷积盲源分离算法须解决不同频点的排序歧义性问题。针对排序问题,本文结合IF-Murata排序法的影响因子,提出了改进的FR-Murata频域卷积混合盲源分离排序法。算法中同时引入了权重系数和影响因子,考虑了频距和频质的影响,以及分离矩阵行列式的连续性,使频点以可靠频点为依据处于更准确的位置,从而提高了算法的稳定性和分离信号精度。仿真实验结果中,FR-Murata算法的相似系数与传统Murata算法相比平均提高了约0.1,在SIR、SDR、SAR的分离性能上均有大幅度的提升,表明了算法的有效性。