基于热平衡法生成同时发生设计日的方法研究

陈友明 ，郭莹 ，宁柏松 ，方政诚 ，刘佳明

［1.湖南大学 土木工程学院，湖南 长沙 410082；2.郑州大学 水利与土木工程学院，河南 郑州 450001；3.建筑安全与节能教育部重点实验室（湖南大学），湖南 长沙 410082］

空调系统设计负荷计算的准确性决定空调系统投资和运行能效.若空调系统设计负荷计算值过大，会导致空调系统设备容量的选择大于实际需求容量，长时间以低负荷率运行，使空调系统设备的运行性能偏离其最佳运行性能，增大空调系统能耗；若空调系统设计负荷计算值过小，会导致空调系统设备容量的选择小于实际需求容量，无法满足人们对室内环境舒适度的要求［1］.合理、准确的设计日能够使空调系统设计更加贴近实际，然而我国现行标准［2］中构造的设计日存在不合理性，本文将其构造的设计日命名为传统设计日.传统设计日的气象参数主要有干球温度、湿球温度和太阳辐射，干球温度是根据历年平均不保证50 h的干球温度和室外温度逐时变化系数确定的，湿球温度是采用历年平均不保证50 h 的湿球温度，太阳辐射是根据当地的地理纬度、大气透明度和大气压力，按7 月21 日的太阳赤纬计算确定的.可以看出传统设计日的气象参数都是独立统计确定的，并未考虑空调室外计算气象参数之间的同时发生性，构造出的设计日较极端，不是真实存在的，会造成不准确的设计负荷计算［3］.

目前已有相关研究提出“同时发生设计日”的概念，同时发生设计日是历年实际存在的气象日，该气象日的各气象参数是同时发生与记录的.文献［4］表明同时发生设计日各气象参数的日分布曲线比传统设计日更加合理且贴近实际.在以往关于同时发生设计日的研究中，主要是基于传递函数法［5］和周期反应系数法［5］生成的.文献［6］表明用传递函数法生成的同时发生设计日计算设计负荷是不够准确的，正确率仅有70%左右，为了得到较高的准确率，需要生成一个48～72 h时间序列的气象参数，显然不适合工程应用.文献［6］指出虽然在理论上周期反应系数法计算设计负荷的精度略低于传递函数法，但总体上基于周期反应系数法生成的同时发生设计日比基于传递函数法生成的同时发生设计日更适合工程应用.热平衡法是目前最准确的负荷计算方法［7］，但是相对比较复杂，计算量大且周期长，基于热平衡法进行的相关研究相对较少.本研究充分考虑建筑类型，将热平衡法与综合聚类法相结合，实现生成空调系统精细化设计用同时发生设计日，通过对比同时发生设计日和传统设计日的设计负荷与理论设计负荷的差异率评价热平衡法生成同时发生设计日的适用性.

1 热平衡法模型及输入参数

1.1 热平衡法模型

热平衡方程组主要包括房间各围护结构离散层节点与空气节点的热平衡方程组.空气节点热平衡方程基于两个假设：一是室内空气温度均匀；二是室内空气对辐射完全透明，不吸收长波辐射［8］.本文的目的是生成同时发生设计日的室外计算参数，无须考虑内扰的影响，房间负荷主要来源于太阳辐射、围护结构传导和新风渗透，热平衡法负荷计算原理如图1所示.

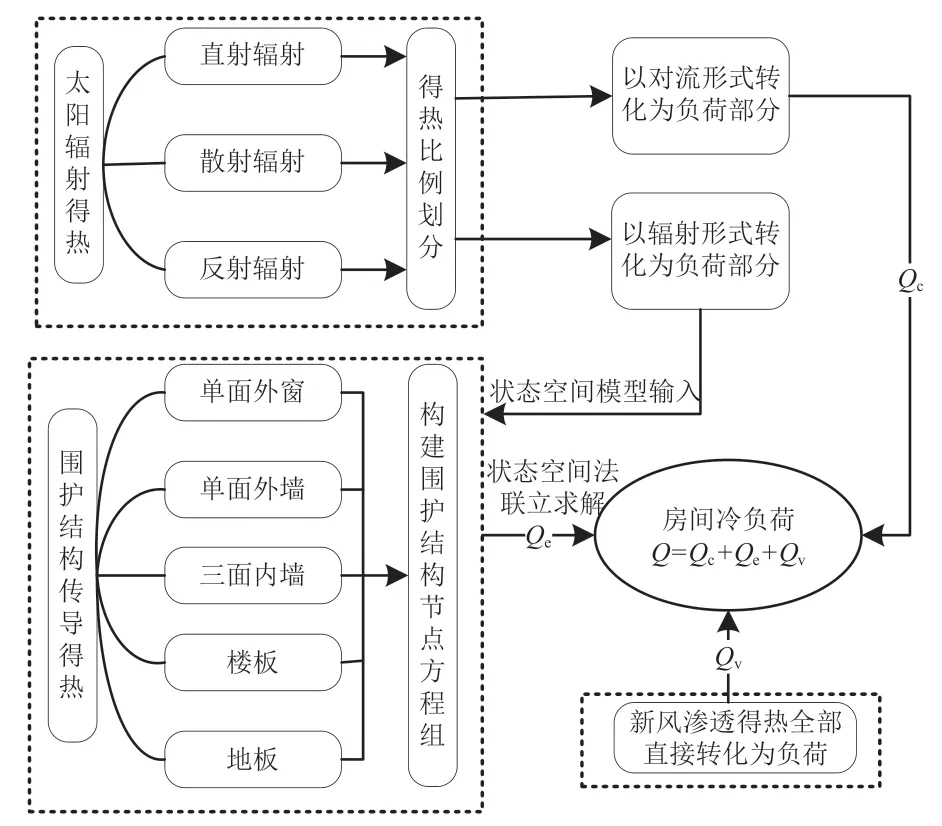
图1 热平衡法负荷计算原理Fig.1 The load calculation principle of heat balance method

1.1.1 太阳辐射冷负荷

式中：Awin为窗户面积，m2；Etb、Etd、Etr分别为太阳直射辐射、散射辐射、反射辐射，W∕m2；Fb为太阳直射辐射得热的辐射分数，即太阳直射辐射得热中以辐射形式转化为负荷的比例；Fd为太阳散射辐射和反射辐射得热的辐射分数，即太阳散射辐射和反射辐射得热中以辐射形式转化为负荷的比例，当SHGC＞0.5时，Fd为0.33，当SHGC≤0.5 时，Fd为0.46；IAC 为内遮阳衰减系数；qb为太阳直射辐射得热，W；qd为太阳散射辐射和反射辐射得热，W；Qc为太阳辐射得热中以对流形式转化的负荷，W；Qr为太阳辐射得热中以辐射形式转化的负荷，W；SHGCθ为太阳直射辐射的太阳辐射得热系数；SHGC为太阳散射辐射和反射辐射的太阳辐射得热系数.

1.1.2 围护结构传导冷负荷

式中：hc，i为围护结构内表面对流换热系数，W∕（m2·℃）；i为房间围护结构内表面数量，房间共有7个围护结构内表面，分别为1 个外墙内表面、外墙上1 个窗户内表面、3 个内墙内表面、楼板内表面、地板内表面；Qe为围护结构传导冷负荷，W；Ti为围护结构内表面温度，℃；Tr为室内设置温度，℃.

1.1.3 新风渗透冷负荷

式中：cp为空气定压比热容，J（∕kg·℃）；ma为新风渗透空气质量流量，kg∕s；Qv为新风渗透冷负荷，W；Tg为室外空气干球温度，℃；wo为室外空气含湿量，kg∕kg；wi为室内空气含湿量，kg∕kg；γ为空气潜热，J∕kg.

1.1.4 房间总冷负荷

式中：Q为房间总冷负荷，W.

1.2 围护结构节点方程

房间围护结构包括1面外墙、外墙上1扇窗户、3面内墙、楼板、地板.已知围护结构材料层数为n层，然后根据围护结构每层的材料和厚度确定其节点数J.假设每个离散层材料物性均匀，再将围护结构各离散层节点由室内向室外进行编号，第m层材料的第k个节点编号为mk.最后对所有节点建立热平衡方程，采用状态空间法对各围护结构节点方程联立求解，就可以计算出各围护结构内表面的温度.各围护结构节点设置如图2所示.

图2 围护结构节点设置Fig.2 The settings of envelope

1）第1 层材料内表面离散层节点11的热平衡方程为：

2）第m层材料离散层节点m1（该节点的控制单元体由第m层材料的半个空间步长的区域和m-1层材料的半个空间步长的区域构成）的热平衡方程为：

3）第m层材料离散层节点mk（k=1，2，…，J-1，该节点的控制单元体由第m层材料中的一个空间步长的区域构成）的热平衡方程为：

4）第n层材料离散层节点nJ的热平衡方程为：

式中：A为围护结构的面积，m2；Cm为第m层材料的热容，J∕℃；hc为围护结构内表面的对流换热系数，W∕（m2·℃）；hr为围护结构内表面辐射换热系数，W∕（m2·℃）；ho为围护结构外表面综合换热系数，W∕（m2·℃）；q0为围护结构内表面接收的各种扰动输入，W∕m2；Rm为第m层材料节点间的热阻，（m2·℃）∕W；Tmk为第m层材料第k节点的温度，℃；Te为室外空气综合温度，℃；Ti为其余6 个围护结构内表面中第i个围护结构内表面节点的温度，℃；Tr为室内空气温度，℃；τ为时间，s.

1.3 状态空间模型

状态空间模型常用于分析有多个输入和输出的线性系统，通过使用有限差分或有限元方法将传热问题表述为状态空间表示形式.1.2 节中的节点方程组可以写成具有N个状态、P个输入和M个输出的连续性时不变系统的状态空间方程，如式（12）和式（13）所示，式（12）称为状态方程，式（13）称为输出方程.

式中：x为N个状态变量组成的向量，如未知温度；τ为时间，s；y为输出向量，如热导率；u为P个输入组成的向量，即扰动变量；A为N×N阶常系数矩阵；B为N×P阶常系数矩阵；C为M×N阶常系数矩阵；D为N×P阶常系数矩阵.

A、B、C、D矩阵均为与房间围护结构热特性相关的常系数矩阵［9］.房间扰动向量u的输入包括室外干球温度、邻室温度、室内空气温度、人员、设备、灯光、太阳辐射（以辐射形式转化为负荷的部分）、太阳辐射部分作用下的围护结构外表面温度等所有影响房间负荷的因素.通过联立求解状态空间方程，可以得到围护结构各节点的温度.

2 评价方法概述

2.1 同时发生设计日的生成

基于热平衡法生成同时发生设计日的步骤为：1）用各城市长年逐时历史气象数据和热平衡法负荷计算模型计算各城市房间连续逐时动态负荷；2）根据，历年平均不保证50 h［10］确定理论设计负荷，与传统设计日不保证水平一致；3）以理论设计负荷为依据采用综合聚类法［11］挑选同时发生设计日.综合聚类法通过在理论设计负荷附近设定设计负荷的偏差阈值确定同时发生设计日集，通过加权方法将每个设计日的逐时室外干球温度、室外湿球温度、太阳辐射照度和冷负荷4 个特征组合为一个合成矢量，依据层次聚类法划分得到设计日主簇，计算主簇4 个特征的中心矢量，在设计日集中与4 个特征的中心矢量的距离最接近的设计日即为最终挑选出的具有代表性的同时发生设计日.

房间连续逐时动态负荷计算需要统计年份的历史逐时室外气象参数和房间特征参数.

1）室外气象参数

室外气象参数的统计年份宜取20～30年［2］.气象参数主要信息包括干球温度、湿球温度、法向直射辐射、水平面散射辐射等.此外，为研究不同城市的适用性，需依据建筑热工设计分区选择相应的代表城市.这里以哈尔滨、北京、长沙和广州分别作为严寒地区、寒冷地区、夏热冬冷地区和夏热冬暖地区的代表城市，表1给出了各城市具体信息.

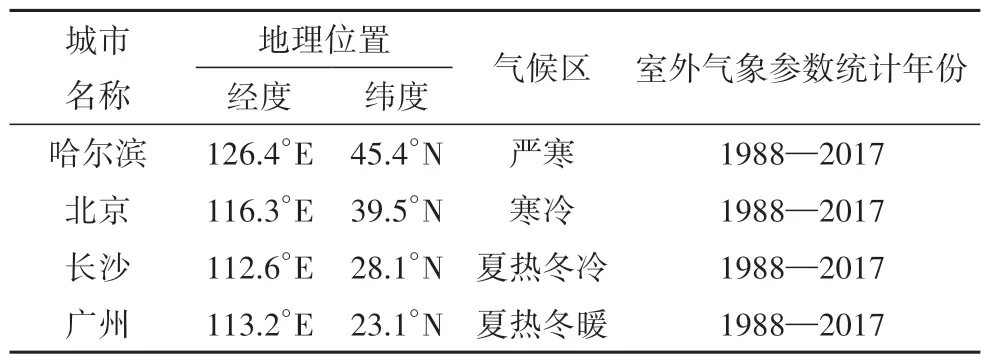
表1 各城市信息Tab.1 Information of each city

2）房间特征参数

热平衡法负荷计算模型所需的房间特征参数包括5 种围护结构类型、窗墙比、房间长度、房间进深、新风系数［12］、内遮阳衰减系数、围护结构外表面吸收率、太阳直射辐射得热的辐射分数、太阳直射辐射的太阳得热系数、太阳散射辐射和反射辐射的太阳得热系数.表2给出了各参数取值.

表2 房间特征参数种类及其取值Tab.2 Types and value of room characteristic parameters

考虑到由14 种特征参数的不同取值组合而成的房间样本过多，无法对所有房间样本进行计算.文献［13］研究表明，当样本总量超过1 000 万时，采用0.025%抽样比或抽取大约2 500 个样本就可以得到较为精确的结果.采用蒙特卡罗方法随机抽取表2中的14 种特征参数组合.除此之外，外墙的朝向也是需要考虑的一个重要参数，这里考虑了8 个朝向，分别为东、东南、南、西南、西、西北、北、东北.本研究中随机抽取了3 000个样本房间，对每一个样本房间的8个朝向进行模拟计算.若将房间朝向作为其中1个房间特征参数，则样本房间总量为2.4万.

2.2 适用性评价流程

通过对比同时发生设计日的设计负荷差异率与传统设计日的设计负荷差异率评价热平衡法生成同时发生设计日的适用性.图3 给出了用热平衡法生成同时发生设计日的适用性评价流程.

图3 同时发生设计日的适用性评价流程Fig.3 The suitability evaluation process for coincident design day

同时发生设计日的设计负荷差异率计算如图3左侧所示：1）依据某城市历年实测逐时气象参数和某一房间特征参数，用热平衡法计算其历年连续逐时动态负荷Q0；2）根据历年平均不保证50 h 确定理论设计负荷Qd0；3）以理论设计负荷Qd0为依据，用综合聚类法挑选同时发生设计日；4）依据同时发生设计日气象参数和同一房间特征参数，用热平衡法计算其24 h 逐时冷负荷Q1，其峰值负荷即为同时发生设计日的设计负荷Qd1（以下简称同时发生设计负荷）；5）计算同时发生设计负荷Qd1与理论设计负荷Qd0的差异率E1.

传统设计日的设计负荷差异率计算如图3 右侧所示：1）依据传统设计日气象参数和同一房间特征参数，用热平衡法计算其24 h逐时冷负荷Q2，其峰值负荷即为传统设计日的设计负荷Qd2（以下简称传统设计负荷）；2）计算传统设计负荷Qd2与理论设计负荷Qd0的差异率E2.

3 结果与讨论

3.1 统计结果

按照图3 的步骤计算各代表城市不同朝向各3 000 个样本房间的同时发生设计日的设计负荷差异率和传统设计日的设计负荷差异率，统计结果分别如图4～图7所示.

图4 两种设计日的设计负荷差异率（哈尔滨）Fig.4 Difference rate of design load between two design days（Harbin）

3.1.1 哈尔滨

哈尔滨样本房间的统计结果如图4 所示，同时发生设计日的设计负荷差异率分布范围远小于传统设计日，各朝向的差异率分布范围基本一致.这说明，与传统设计日相比，同时发生设计日计算设计负荷更准确.哈尔滨5%～95%样本房间的同时发生设计日的设计负荷差异率分布范围为-3.2%～9.9%.传统设计日的设计负荷差异率较大，各朝向差异率分布范围不同，其中东和东北朝向差异率分布范围最大，北朝向差异率分布范围最小.以各朝向5%～95%样本房间为例，东、东北朝向样本房间的差异率分布范围为7.8%～109.8%，东南朝向样本房间的差异率分布范围为11.1%～70.7%，北朝向样本房间的差异率分布范围为-8.5%～10.6%，其他朝向样本房间的差异率分布范围为5.6%～37.0%.

3.1.2 北京

北京样本房间的统计结果如图5 所示，同时发生设计日的设计负荷差异率较小，各朝向的差异率分布范围基本一致.这说明，与传统设计日相比，同时发生设计日计算设计负荷更准确.北京5%～95%样本房间的同时发生设计日的设计负荷差异率分布范围为-1.9%～7.6%.传统设计日的设计负荷差异率较大，各朝向差异率分布范围不同，其中东朝向差异率分布范围最大，北朝向差异率分布范围最小.以各朝向5%～95%样本房间为例，东、西、西北和东北朝向差异率分布范围为5.9%～67.4%.东南、西南朝向样本房间的差异率分布范围为7.3%～46.2%，南朝向样本房间的差异率分布范围为2.0%～23.0%，北朝向样本房间的差异率分布范围为0.7%～12.6%.

图5 两种设计日的设计负荷差异率（北京）Fig.5 Difference rate of design load between two design days（Beijing）

3.1.3 长沙

根据图6 长沙的统计结果，同时发生设计日的设计负荷差异率远小于传统设计日，各朝向的差异率分布范围基本一致.这说明与传统设计日相比，同时发生设计日计算设计负荷更准确.长沙5%～95%样本房间的同时发生设计日的设计负荷差异率分布范围为-1.3%～5.0%.传统设计日的设计负荷差异率较大，各朝向差异率分布范围不同，其中西和西北朝向差异率分布范围最大，北朝向差异率分布范围最小.以各朝向5%～95%样本房间为例，西和西北朝向样本房间的差异率分布范围为6.8%～47.1%，东和东北朝向样本房间的差异率分布范围为5.2%～34.3%，东南和西南朝向样本房间的差异率分布范围为3.9%～22.6%，南朝向样本房间的差异率分布范围为-14.3%～5.5%，北朝向样本房间的差异率分布范围为-6.5%～6.0%.

图6 两种设计日的设计负荷差异率（长沙）Fig.6 Difference rate of design load between two design days（Changsha）

3.1.4 广州

根据图7 广州的统计结果，同时发生设计日的设计负荷差异率远小于传统设计日，各朝向的差异率分布范围基本一致，这说明，与传统设计日相比，同时发生设计日计算设计负荷更准确.广州5%～95%样本房间差异率分布范围为-0.8%～4.8%.传统设计日的设计负荷差异率较大，各朝向差异率分布范围不同，其中东和东北朝向差异率分布范围最大，西南朝向差异率分布范围最小.以各朝向5%～95%样本房间为例，东和东北朝向样本房间的差异率分布范围为3.9%～61.1%，西和西北朝向样本房间的差异率分布范围为4.2%～34.8%，南朝向样本房间的差异率分布范围为-24.8%～ -1.7%，东南朝向样本房间的差异率分布范围为2.5%～22.1%，北朝向样本房间的差异率分布范围为-14.5%～2.4%，西南朝向样本房间的差异率分布范围为-4.4%～10.7%.

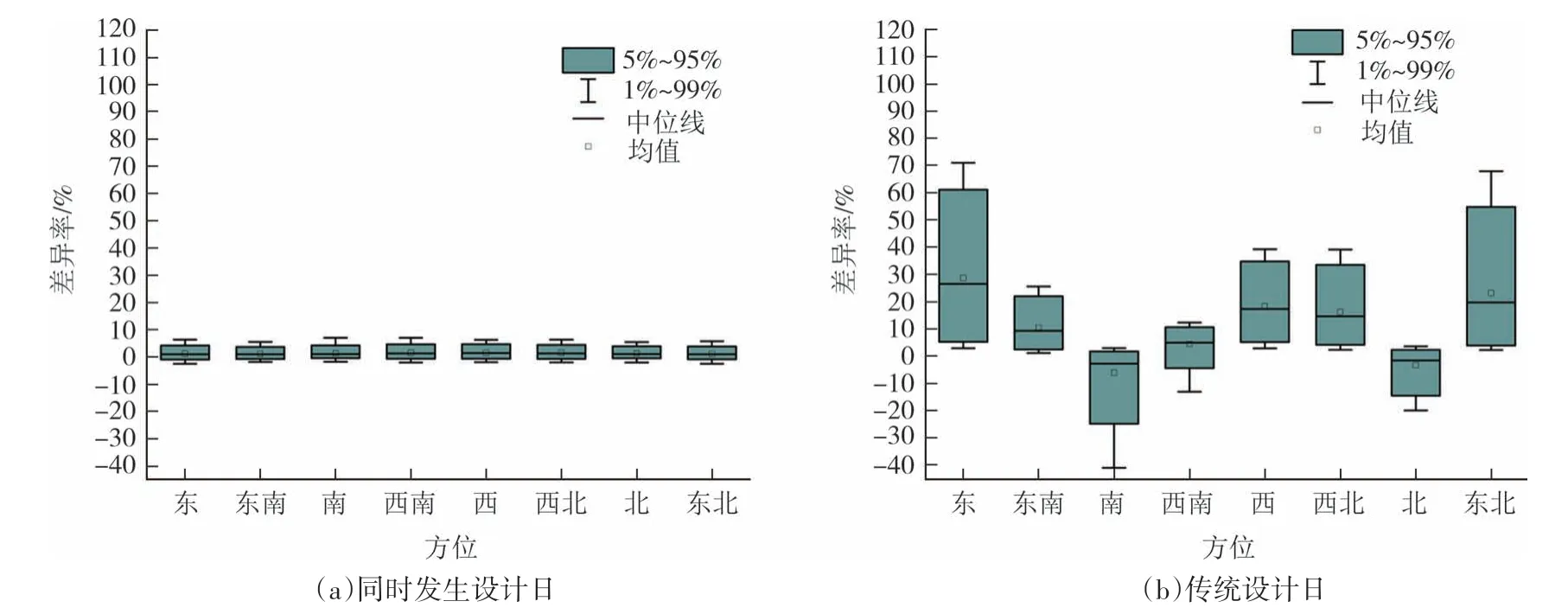
图7 两种设计日的设计负荷差异率（广州）Fig.7 Difference rate of design load between two design days（Guangzhou）

3.2 讨论

为使基于热平衡法生成同时发生设计日的方法研究更加完善，对以下几点内容进行讨论.

1）两种设计日的设计负荷差异率存在的原因.传统设计负荷与理论设计负荷出现偏差主要是因为传统设计日不是实际存在的气象日，各气象要素的参数值是独立统计确定的，彼此之间没有关联性，而理论设计负荷是用历年实际存在并记录的气象参数计算得到的.同时发生设计负荷与理论设计负荷虽然都是用实际存在的气象数据计算的，但是理论设计负荷是用历年逐时气象参数迭代计算的，而同时发生设计负荷仅仅是用同时发生设计日的气象参数迭代计算的.

2）不同朝向房间传统设计日的设计负荷差异率分布范围不同.对于房间特征参数相同但朝向不同的房间来说，太阳辐射最大值出现时刻肯定是不同的.但是传统设计日构造时只是将7 月21 日各朝向的太阳辐射值作为设计依据，就会高估或低估各朝向的太阳辐射值，使各城市不同朝向房间传统设计日的设计负荷差异率分布大相径庭.为了提高设计日对不同朝向的适用性，文中针对不同朝向房间生成了相应的同时发生设计日，因此各城市不同朝向房间的同时发生设计日的设计负荷差异率分布范围基本相同.

3）不同气候区的差异率分布范围不同.以同时发生设计日的设计负荷差异率为例，从四个代表城市的统计结果可以看出，严寒地区、寒冷地区、夏热冬冷地区和夏热冬暖地区的差异率分布范围逐渐减小.通过对比四个城市中同一房间样本的同时发生设计负荷和理论设计负荷，可以发现，在不同城市同一房间的同时发生设计负荷与理论设计负荷的差值是接近的，但是不同城市理论设计负荷不同，严寒地区最小，夏热冬冷和夏热冬暖地区较大.根据图3 中设计日的设计负荷差异率计算公式可以看出，当理论设计负荷越大时，设计负荷差异率就会越小.

4）热平衡法的优势与不足.热平衡法是用最基本的原理和最少的简化计算房间负荷，是理论上最准确的负荷计算方法.用热平衡法计算房间负荷相对来说准确性更高，也更加接近实际负荷.但是热平衡法比较复杂，计算量大且周期长.这里以某一个城市为例，用配置AMD 3970X 处理器的工作站模拟3 000个样本房间，需要3 d才能完成计算.

4 结论

本文建立了基于热平衡法的负荷计算模型，用长年逐时历史气象参数和热平衡法生成同时发生设计日，通过对比同时发生设计日和传统设计日的设计负荷差异率评价热平衡法生成同时发生设计日的适用性.以四个热工设计气候分区的代表城市哈尔滨、北京、长沙和广州为例，随机抽取3 000个样本房间，对每一个样本房间的8个朝向进行模拟计算.

通过两种设计日的设计负荷差异率对比发现，各城市同时发生设计日的设计负荷差异率分布范围很小，各朝向的差异率分布大致相同.哈尔滨、北京、长沙和广州的5%～95%样本房间同时发生设计日的设计负荷差异率分别为-3.2%～9.9%、-1.9%～7.6%、-1.3%～5.0%、-0.8%～4.8%.而各城市传统设计日的设计负荷差异率分布范围很广，各朝向分布完全不同.哈尔滨传统设计日的设计负荷差异率分布范围最大，东朝向5%～95%样本房间的差异率分布范围高达7.8%～109.8%.长沙传统设计日的设计负荷差异率分布范围最小，北朝向样本房间差异率分布最小，北朝向5%～95%样本房间的差异率分布范围为-6.5%～6.0%.

以上结果表明，各城市同时发生设计日的设计负荷差异率分布范围都远小于传统设计日，同时发生设计日的设计负荷差异率在各朝向的分布基本相同，而传统设计日的设计负荷差异率在各朝向的分布不同.这说明用基于热平衡法生成的同时发生设计日计算房间设计负荷比传统设计日更准确；同时发生设计日对不同朝向房间的适用性比传统设计日更强，更适合工程应用.