基于时间序列ARMA模型的拱桥施工变形预测

张 杰 李庆龄

（1.西华大学建筑与土木工程学院，四川 成都 610039；2.巴中利伟建设工程有限公司成都分公司，四川 成都 610095）

0 引言

钢管混凝土系杆拱桥具有复杂的结构体系，在施工过程中往往存在多种偏差和误差。随着桥梁施工进程的推进，这些偏差和误差会导致主拱肋标高偏离设计目标，影响桥梁的内力和线形，甚至造成合拢困难。因此，在钢管混凝土系杆拱桥施工过程中，针对随时间变化的施工数据进行变形分析和预测，并对过大变形及时采取有效的控制措施，才能确保结构的实际变形符合预期目标[1]。

时间序列分析是一种重要的数学方法，用于处理相互关联的动态数据集合，它可以对随时间变化的数据进行分析和预测。时间序列数据具有独特的特点，即它们随时间的推移而变化，并能够反映过去所有的因果关系[2]。因此，时间序列分析能够揭示数据随时间变化的规律，帮助建立可预测性模型，以指导决策和规划。与传统的统计分析方法不同，时间序列分析更注重时间的因素，将时间作为自变量，从而代替复杂的影响因素和数据缺失等问题[3]。

在工程结构监测领域，时间序列分析的应用较少，这是由于工程结构本身的特点和监测数据的不确定性等因素所致。然而，在房屋结构和隧道变形监测中，时间序列分析已经被广泛应用，并且在处理监测数据方面具有显著的优越性[4]。时间序列分析可以有效地处理监测数据，用于桥梁施工监测过程中的变形分析，并且具有很好的应用前景。然而目前国内在桥梁施工监测过程中使用时间序列分析的研究仍然相对较少[5]。基于此，本文利用时间序列ARMA 模型对某特大桥主桥施工监控过程中主拱肋控制点变形数据进行分析，以促进该分析方法在桥梁施工监测中的应用。

1 工程概况与施工变形监测

1.1 工程概况

依托工程为一座飞燕式钢管混凝土系杆拱桥。桥梁跨径布置为（30m+120m+30m），桥梁总长180m，桥宽61.3m，设计汽车荷载为-A 级。该大桥的缆索吊装布置如图1所示。

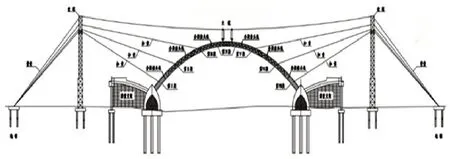
图1 某特大桥缆索吊装布置图

1.2 施工变形监测

编制该大桥主桥施工监控方案并采用全站仪及专用棱镜对拱肋进行变形监测。主拱肋变形测点根据拱肋分段情况和结构变形情况进行布置，每个拱肋分段布设一个监测断面。为避免梁段焊接影响，监测断面布置在距离梁段边缘0.5m 处，共布置7个断面；每个断面各布置4 个测点，位于钢管拱肋顶端，全桥共布置28个测点。

2 建立时间序列模型的基本思想

时间序列分析的核心理念是同一变量在不同时间点上的观测值之间存在一定的关联性。这种关联性意味着过去的观测值可以用来预测未来的观测值，虽然在新的时刻仍然可能出现不可预测的情况。因此，可以通过建立一个描述时间序列的模型，来研究和预测这个序列在未来的变化趋势。具体地说，若记Xt（t=…,-2,-1,0,1,2,…）是一个无限时间序列，那么时间序列模型就是一个用来描述这个序列的数学模型，如公式（1）所示。

3 时间序列ARMA模型的建立及预测分析

3.1 数据预处理

进行平稳性检验是时间序列建模的必要前提之一，因为时间序列的平稳性对建模至关重要。确保时间序列的平稳性是为了确保模型的可靠性和准确性。下文对最上游拱肋跨中4号断面测点（简称D4测点）施工阶段CS7-CS29 的变形数据进行分析。使用Eviews软件计算序列r的自相关函数和偏相关函数，相关系数和趋势见图2所示。

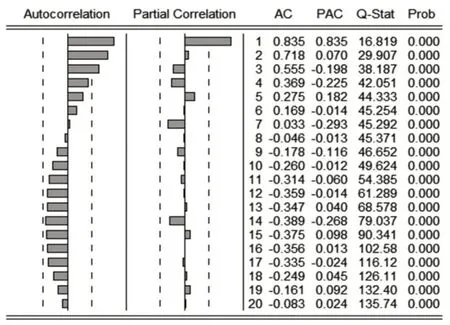
图2 序列r的自相关图与偏相关图

在本例中，只关注自相关函数，而Eviews提供了自相关函数(AC）和偏自相关函数(PAC)。使用自相关函数图可以判断序列的稳定性：如果自相关系数快速趋近于0 并落入随机区间，则时间序列是平稳的；反之，如果趋势缓慢或不断递增，且在第8 期后数据符号改变，则表明序列r存在趋势性，是非平稳的。

经过对序列r进行ADF 单位根检验，得到的p 值为0.9919，大于显著性水平0.05。根据显著性检验结果，可以得出结论：序列r是非平稳的。这意味着在时间序列建模中，如果直接使用序列r 进行回归分析，可能会遇到虚假回归问题。为了避免这个问题，需要对序列r进行处理，使其变为平稳序列。常用的方法是进行差分操作，通过计算相邻观测值之间的差异来获得差分序列dr。差分序列dr消除了序列中的趋势和季节性等非平稳因素，使得序列变得平稳。利用差分序列dr 进行进一步的时间序列建模分析，可以得到更可靠的结果，并避免虚假回归问题的影响。因此，在本例中，将对原始序列r 进行一阶差分操作，生成差分序列dr，然后利用差分序列dr 进行时间序列建模分析，以获得更准确和可靠的结果。观察序列dr的自相关函数和偏相关函数，相关系数和趋势见图3所示。

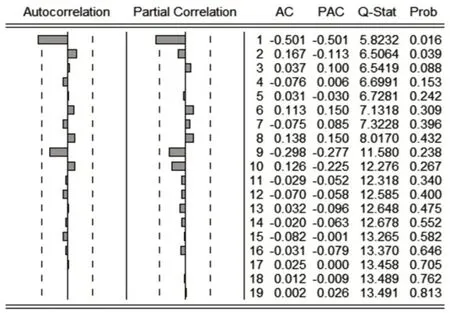
图3 序列dr的偏自相关系数

根据观察，从图3 中可以发现差分序列dr 的自相关图和偏相关图都呈现明显的截尾现象，这表明差分序列dr 满足平稳性的条件。为了进一步验证这一点，对差分序列dr 进行ADF 检验。根据检验结果的t 统计量，其实际p 值为0.0000，小于设定的显著水平0.05。因此，经过显著性检验，可以得出结论，序列dr 不存在单位根，表明该序列已经处于平稳状态。

3.2 模式识别

根据样本的自相关函数和偏相关函数的截尾性质，可以初步判断序列为自回归滑动平均模型（ARMA）中的ARMA(1,2)模型。同时，需要考虑临近的几个模型，包括自回归模型AR(1)和AR(2)，滑动平均模型MA(1)和MA(2)，以及ARMA 混合模型ARMA(1,1)、ARMA(1,3)、ARMA(2,1)和ARMA(2,2)。

3.3 参数估计

本文中使用常用的最小二乘法进行参数估计，得出了各个模型的参数估计值，见表1所示。

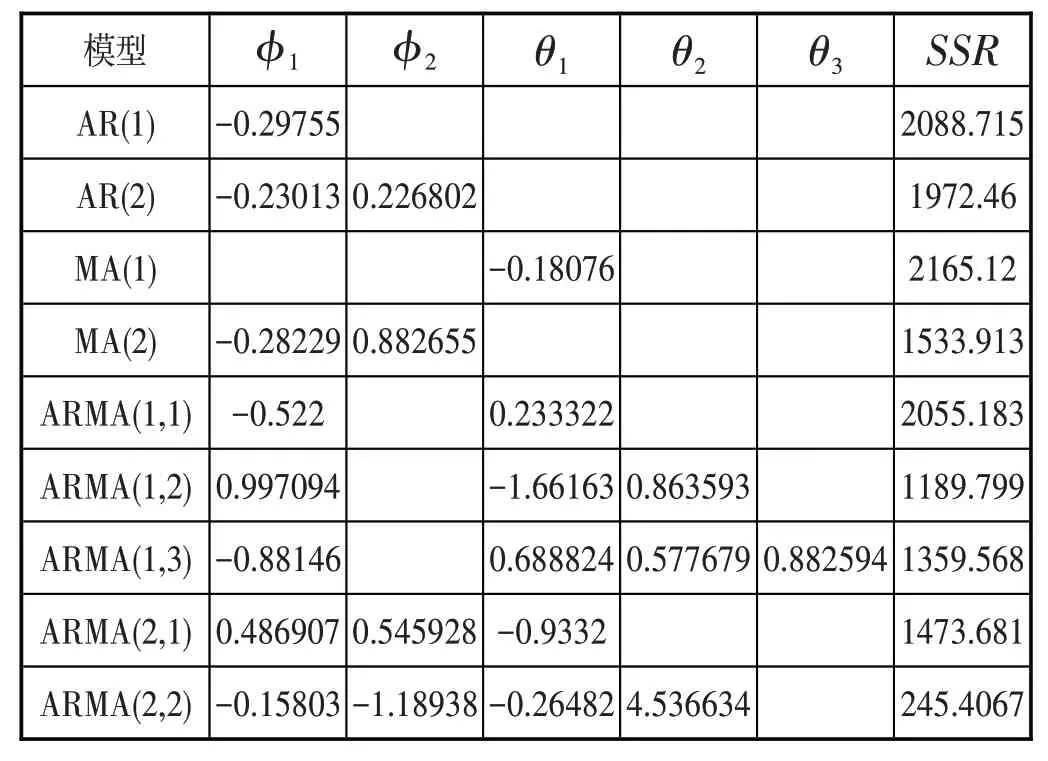
表1 模型的参数估计值

3.4 模型定阶

各阶模型AIC 和BIC 准则值，见表2。从表2 中可以看出：AIC 值较小的有ARMA(1,2)，ARMA(1,3)，ARMA(2,2)和MA(2)模型，SIC 值较小的也是ARMA(1,2)，ARMA(1,3)，ARMA(2,2)和MA(2)模型。根据HQ 准则，ARMA(1,2)、ARMA(1,3)、ARMA(2,2)和MA(2)模型具有较小的HQ 值，因此被认为是较为合适的模型。使用Eviews计算这些模型的统计检验量结果见表3。

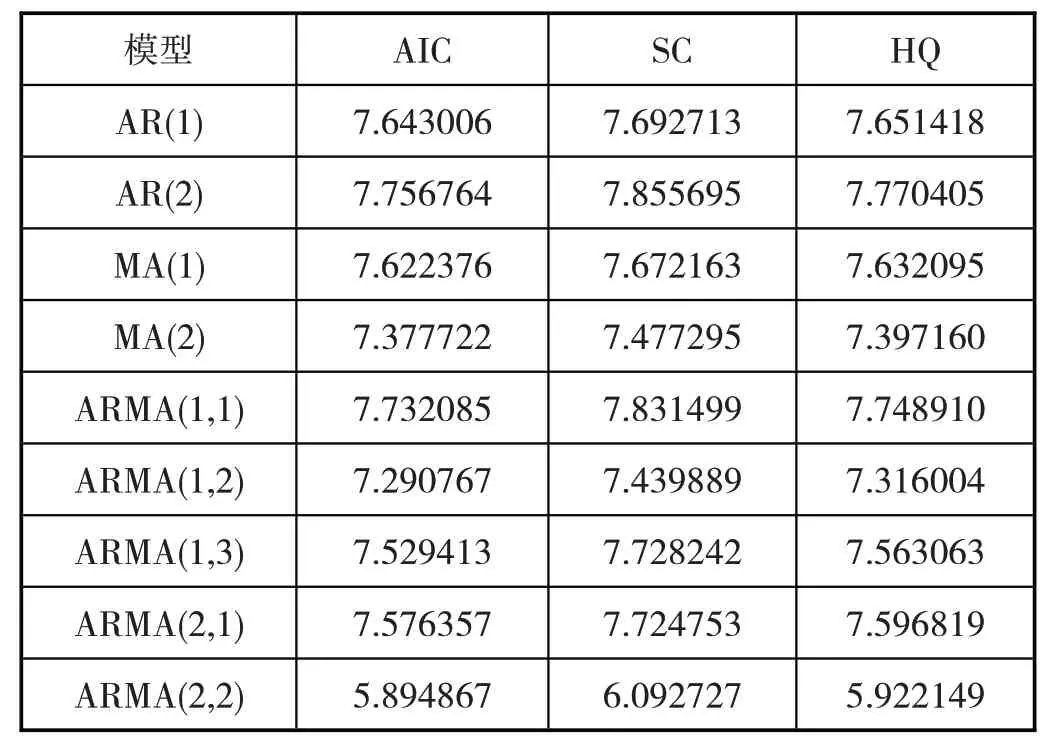
表2 序列dr的各阶模型定阶准则值

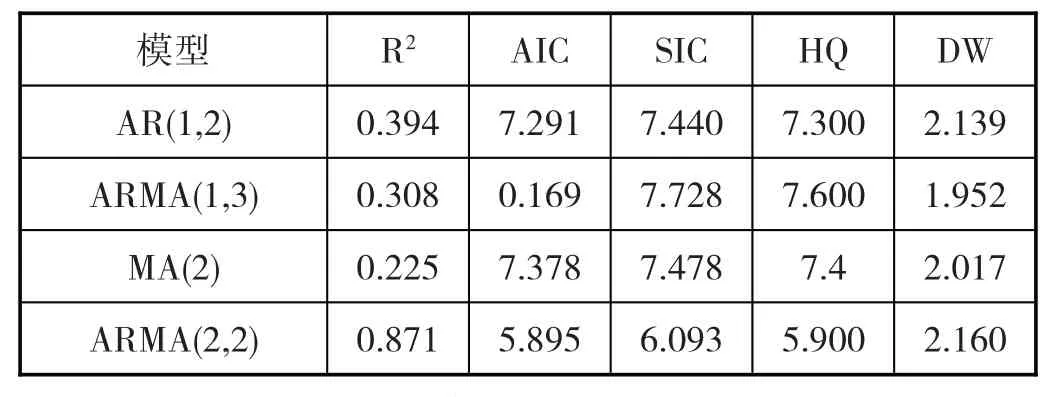
表3 各模型检验量

模型的优选主要依赖于以下几个评价指标的对比：决定系数R²，其数值范围为0 至1，越接近1 则代表模型拟合的效果越佳。再者，赤池信息准则(AIC)，其数值越小，表明模型的精度越高。另一项是施瓦兹贝叶斯信息准则(SIC)，其数值越小则表明模型更为精确。最后，Durbin-Watson 统计量，当数值在1.8 到2.1 之间时，表示残差序列呈现出正态分布且无相关性。

通过表3的比较可得：ARMA(2,2)模型虽然其AIC、SIC 信息量较小，但Prob 值≥0.05，即模型不显著，不能拒绝原假设，因此不适用于本研究。ARMA(1,2)模型的拟合优度R2最高，同时其AIC、SC 值也最小。综合考虑，选择采用ARMA(1,2)模型。

3.5 残差检验

3.5.1 平稳性检验

对于ARMA(1,2)模型，自回归部分特征根为：λ=[1]，绝对值|λ|=[1]；滑动平均部分特征根为：v=[0.83-0.42i,0.83+0.42i]，绝对值 |v|=[0.9405,0.9405]；即 |λi|≤1,|vi|≤1(i= 1,2)，满足平稳可逆条件，因此，模型是平稳可逆的。

3.5.2 正态性检验

对于ARMA(1,2)模型，将估计的参数代入计算，从t=p+1=2开始计算残差序列at，同时将未知的a值和x值设为零，通过递推方法求得模型的残差。然后，使用Eviews 对残差进行LM 检验，得到的LM 检验结果为0.9876。根据检验结果，P值大于0.05，说明残差序列呈正态分布。

3.5.3 白噪声检验

为了验证ARMA(1,2)模型的残差是否具有白噪声特性，选定滞后阶数k=12，并计算了残差的自相关函数（ACF）值以及Q 统计量。根据Eviews 计算结果可得出，残差序列的自相关函数值在Bartlett范围内，表明残差序列之间相互独立。滞后12阶的Q 统计量的P 值均大于显著性水平0.05，表示接受原假设，即残差序列不相关或相互独立。对残差序列进行ADF 单位根检验，发现t统计量绝对值大于1%、5%、10%三个显著性水平的t值，且p值为0.0017，小于这三个显著性水平。因此，可以拒绝原假设，并得出结论：残差序列不存在单位根。综上所述，当假设序列DR 为ARMA(1,2)时，可以认定其残差序列可以视为白噪声，即序列的随机性已经被成功捕捉。

3.6 预测分析

通过差分方程形式进行向前一步预测，可以获得ARMA(2,1)模型的预测结果，具体为：

代入已知数值和模型的参数估计值，可求出序列dr的预测值为：

得到序列的拟合数据以及预测数据可见图4的D4测点拱肋变形值预测效果比较图。

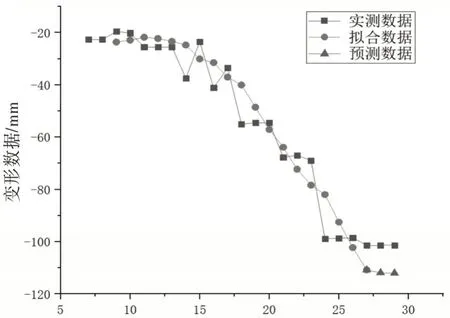
图4 D4号测点拱肋变形值预测效果比较图

由图4 可以看出用ARMA 模型进行预测的最大拟合误差为12.7mm，最大预测误差为10.6mm。该模型预测效果较好，具有较高的精度。

4 结束语

（1）时间序列ARMA 模型可以精准拟合与预测拱桥拱肋在建设过程中的变形值，使得钢管混凝土拱桥的施工控制得到有效保障，钢管混凝土拱桥的建设过程更加安全与高效。

（2）采用时间序列方法建模时，针对自回归滑动平均模型的参数估计特征，提出了参数估计的“两步走”，即“先参数初估计，然后精确估计参数”。本文计算结果表明这样处理可大大地改善参数的估计精度，提高模型的预测效果。