压敏结构对柔性传感器性能增强的仿真分析*

魏 国，廖宁波，章 城

（1.温州大学机电工程学院，浙江 温州 325035；2.浙江省激光加工机器人重点实验室激光加工机器人示范型国际科技合作基地，浙江 温州 325035）

0 引 言

在压阻层引入压敏结构是提高压阻传感器灵敏度的有效方法［1～4］。Peng S 等人［5］在聚二甲基硅氧烷（polydimethylsiloxane，PDMS）上喷涂导电碳纳米纤维（carbon nanofiber，CNF），在传感器压阻层制备金字塔、半圆球、半圆柱3种压敏结构。实验表明，半圆球的灵敏度最高，达到-3.6 kPa-1。Zhao T等人［6］以金叶和糖为模板，设计和制备了一种基于混合多孔微结构的柔性压阻式压力传感器，灵敏度达到83.9 kPa-1（＜140 Pa），检测限最低为0.5 Pa。综述可知，不同压敏结构对柔性压力传感器灵敏度提升效果不同，需要合理设计压敏结构，并研究其对压力传感器作用机制。

石墨烯基材料作为优良的材料，近年来被广泛研究和应用于柔性压力传感器。Ye X 等人［7］使用聚乙烯亚胺（polyethylenimine，PEI）和还原氧化石墨烯（reduced graphene oxide，rGO），通过化学逐层自主装制备了应变传感器，具有高灵敏度，超低检测限，快速响应的特性。Zhu Y等人［8］使用激光在PDMS上加工rGO 制备的传感器具有较高灵敏度、和较快响应特性。吴志强等人［9］将rGO 和纳米纤维素（nanocellulose，NC）按照10∶3的比例混合，制备出NC／rGO／PDMS的应变传感器，应变灵敏度为63，电导率为0.34 S／m。Wu S等人［10］在复合材料加入了CNF，制备了应变传感器，具有较高的导电率和压阻敏感性。Zhang F 等人［11］使用石墨烯纳米颗粒（graphene nanoparticles，GNPs）、CNF和PDMS制备的传感器，极大改变了线性范围，并达到了50%。因此，石墨烯基柔性压力传感器已经得到了广泛的关注和研究。

综上可知，研究压敏结构对石墨烯基柔性压力传感器的作用机制具有一定意义，然而，压敏结构在压力传感器中的具体形变在实验中难以直接观察。为研究压敏结构具体的形变特性、电阻变化等机制，本文借助有限元仿真软件对基于rGO／PDMS的柔性压阻传感器进行仿真模拟。对比不同压敏结构对复合材料形变、电阻变化和应力分布状况等的影响。验证了压敏结构的存在对传感器灵敏度提升的积极作用，为将来开发柔性压力传感器并提高灵敏度提供了一定参考意义。

1 传感器结构与参数设计

为了具体研究压敏结构对rGO／PDMS柔性压阻式传感器电阻变化的影响，本文在传感器压阻层设计了几种不同类型的压敏结构。如图1所示，为传感器的整体结构图，压敏结构可通过模具倒模制备而成，传感器整体均为同种复合材料，压敏结构位于中间压阻层，包括方柱、圆柱、金字塔、半圆球。方柱和金字塔压敏结构的底边均是边长为20 μm的正方形，高度为10 μm，圆柱和半圆球压敏结构的半径均为10 μm，传感器上顶面和下底面分别外接电极。

图1 传感器压敏结构

为保证结果的准确性，本文根据吴志强等人做的石墨烯基压阻复合材料［9］选择传感器模型和材料进行仿真分析并验证本文的准确性。该文献将rGO、NC和道康宁Sylgard 184硅橡胶按照一定比例均匀混合并加热固化所得的复合材料作为压阻敏感材料。其中，rGO 的质量分数为10%，NC的质量分数为3%时，压阻复合材料的电导率可达到3.4 ×10-1S／m，杨氏模量为2.53 MPa。

2 柔性传感器压阻敏感原理

PDMS柔性聚合物本身是绝缘材料，其电阻率远远大于石墨烯，因此，PDMS 聚合物本身的分子间电流可以忽略。导电复合材料聚合物的导电机制一般用隧道理论效应［12］和导电通道理论效应来解释。复合材料的电阻主要由于电极间导电体和导电通道数目决定。隧道电阻的具体表达式如下［13］

其中，Rm为隧道电阻，V为外加电压，a2为隧道横截面积，J为隧道电流，h为普朗克常量，s为石墨烯片的初始间距，e为基本电荷，m为电子质量，φ为石墨烯片的势垒高度，R0为总电阻，L为一个导电通道中的石墨烯片数量，N0为导电通道数量。

在复合材料受到外部压力时发生形变时，石墨烯片的距离s，导电通路数量N均会发生改变，从而导致复合材料的电阻变化。具体表达式如下［13］

其中，ε为复合材料的弹性应变，Δl为材料复合材料的变形量，l0为复合材料的初始厚度，A和B为导电填料的有关常数，N为导电通路数量，ΔR为复合材料电阻的变化量，不同压阻结构受压后形变如图2所示。

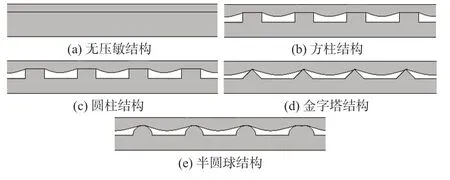
图2 不同压敏结构受压形变

在压阻层引入压敏结构后，柔性压阻传感器在受到外部压力后会让应力集中，传感器的整体形变也会发生改变。在外部载荷不变的情况下，传感器形变会更为明显，从而达到提高传感器电阻变化的幅度，实现传感器灵敏度的提升。

3 柔性压阻传感器仿真与分析

3.1 拉伸仿真与实验数据对比

本文为了保证准确性，首先建立了一组传感模型，具体参数和吴志强等人做的压阻复合材料实验一致［9］，并将结果与实验进行对比。模型如图3 所示，是长宽为80 mm ×10 mm，厚度为1 mm的复合材料薄膜试样，将固体力学与电流进行耦合，设置压阻域电流模块，边界条件为左端面选择固定约束并接地，右端设置拉伸长度并确定端子电流为1 A。

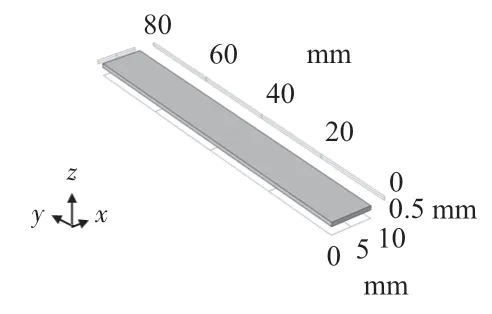
图3 复合材料薄膜试样模型

仿真结果如图4 所示，复合材料薄膜试样应变ε在10%以内时，随着薄膜ε不断增大，薄膜电阻变化率S也在不断增大，并呈线性关系。根据式（7）和式（8），薄膜的灵敏度系数为63，仿真结果和文献中的实验数据基本吻合。

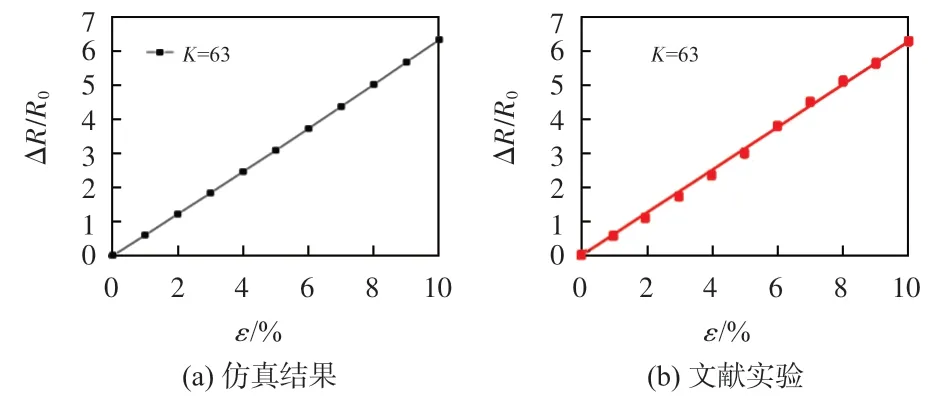
图4 复合材料薄膜试样电阻变化率与应变关系

其中，电阻变化率S和灵敏度系数K计算公式为

式中R0为初始电阻，ΔR为电阻变化量，ε为薄膜试样的应变。

3.2 网格独立性验证

基于上述仿真结果，本节保持材料参数不变，对压敏结构类型不同的石墨烯基压阻传感器进行仿真研究。首先，进行网格独立性验证分析，以确保网格划分的质量不会对计算结果的准确性产生影响。本节选取图5 所示模型的部分单元进行计算，对具有其他压敏结构的传感器选择相同尺寸的模型，对模型划分了不同的单元格数并逐渐加密。设置相应的边界条件：对薄膜的底部进行固定约束，上顶面设置端子，下底面设置接地，在200 Pa 的载荷下计算，分析传感器整体形变状况。

图5 压阻传感器模型的部分单元

石墨烯基压阻传感器模型的网格独立性仿真结果如表1所示，在网格数量加密到一定程度时，网格数量对复合材料位移变化和电阻变化的影响已经不大，本文对无压敏结构，以及方柱、圆柱、金字塔、半圆球压敏结构的传感器模型分别选用41040，63520，41476，83024，86107网格数量进行计算。

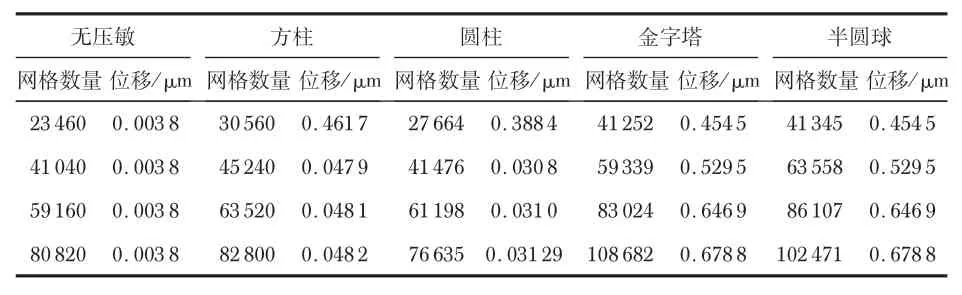
表1 网格独立性验证结果

3.3 载荷对压阻传感器作用仿真分析

为更精确地研究压敏结构对石墨烯基压阻传感器的作用，本文在传感器中选取大小合适的薄膜作为计算模型，模型长宽均为10 μm，高30 μm。分析具有不同微结构的传感器，随着载荷逐渐增大，传感器的形变程度和电阻变化。使用有限元软件的压阻域电流模块计算，边界条件如下：上顶面施加垂直向下的载荷并设置端子电流1 A，下底面固定约束并接地。

根据图6仿真计算结果可知，载荷在0～300 Pa范围内增加时，压敏结构不同的传感器，其位移和电阻变化也在不断增大。其中，金字塔和半圆球压敏结构的传感器的位移和电阻变化提升最为明显，方柱和圆柱以及无压敏结构的传感器变化较为不明显。

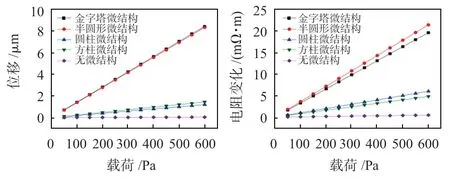
图6 不同压敏结构的传感器受到载荷与位移、电阻变化关系仿真结果

3.4 不同压敏结构类型的柔性压阻传感器仿真分析

为进一步研究压敏结构类型不同的石墨烯基柔性压阻传感器受到外部载荷后的情况，本节对传感器在200 Pa 固定外部载荷的条件下进行仿真分析。载荷方向垂直向下，其余边界条件不变。

3.4.1 无压敏结构的传感器

图7为无压敏结构的传感器在200 Pa固定载荷下的仿真结果，图7（a）为传感器的网格划分，如图7（b）、（c）所示仿真结果可知，传感器在受到外部载荷作用下，传感器的位移主要分布在四周，越靠近中间区域，传感器的位移形变越不明显。这是由于接触面的应力分布同样分布在四周区域，如图7（d）所示。并且分析认为，这也是导致接触面的电阻变化较大的区域同样分布在四周区域的原因之一，如图7（e）所示。

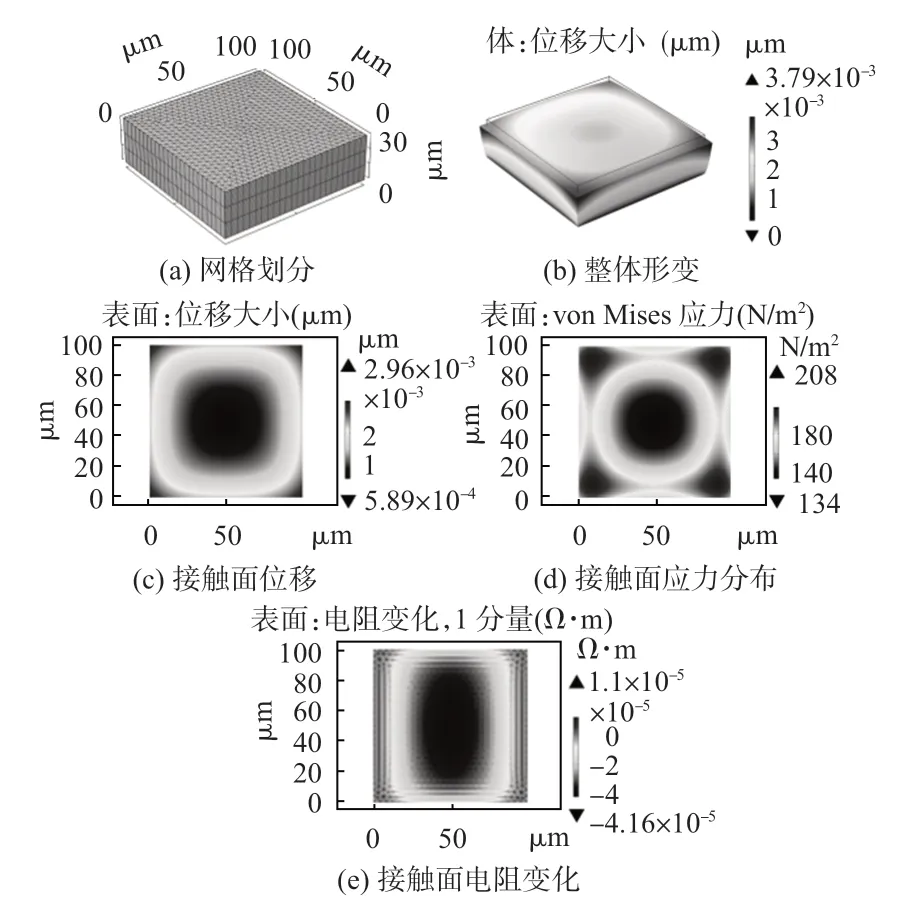
图7 无压敏结构传感器仿真结果

3.4.2 方柱压敏结构的传感器

图8为方柱压敏结构的传感器在20 Pa 固定载荷下的仿真结果，图8（a）为传感器的网格划分，图8（b）～（d）所示仿真结果可知，传感器在受到外部正向载荷后，传感器的位移主要集中在中心区域，越靠近中心区域，传感器的位移越明显。方柱微结构靠近中心区域的部分发生较大位移，这是由于接触面的应力分布集中在方柱微结构靠近中心的区域，如图8（e）所示。由于微结构的引入，传感器中间层中心区域出现空缺，即使在较小的应力条件下，也能发生较大的向下位移形变，因而中心区域电阻变化也较大，如图8（f）所示。

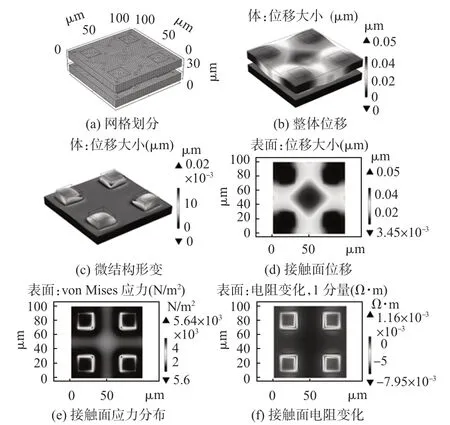
图8 方柱压敏结构传感器仿真结果

3.4.3 圆柱压敏结构的传感器

图9为圆柱压敏结构的传感器在200 Pa固定载荷下的仿真结果，图9（a）为传感器的网格划分，图9（b）～（d）所示仿真结果可知，传感器在受到外部正向载荷后，位移主要集中在中心区域，越靠近中心区域，传感器的位移越明显。圆柱微结构靠近中心区域的部分发生较大位移，这是由于接触面的应力分布集中在方柱微结构靠近中心的区域，如图9（e）所示。由于微结构的引入，传感器中间层中心区域出现空缺，即使在较小的应力条件下，也能发生较大的向下位移形变，因而中心区域电阻变化也较大，如图9（f）所示。

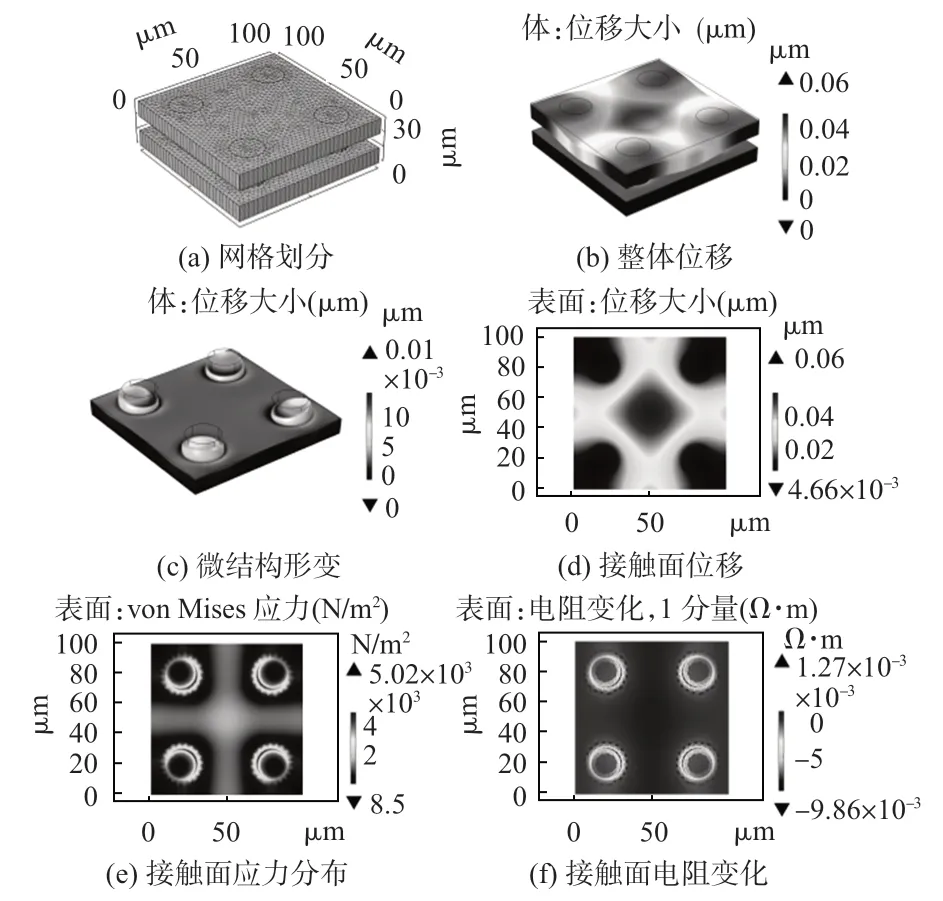
图9 圆柱压敏结构传感器仿真结果

3.4.4 金字塔压敏结构的传感器

图10 为金字塔压敏结构在200 Pa 固定载荷下的仿真结果，图10（a）为传感器的网格划分，图10（b）～（d）所示仿真结果可知，传感器在受到外部正向载荷后，传感器的大部分区域都会向下位移。由于金字塔压敏结构的存在，且金字塔微结构和上层复合材料的接触面积非常小，导致接触面的应力非常集中，如图10（e）所示。这也导致了在金字塔微结构和上层复合材料的接触点附近区域的电阻变化非常大，但变化区域也非常集中，如图10（f）所示。

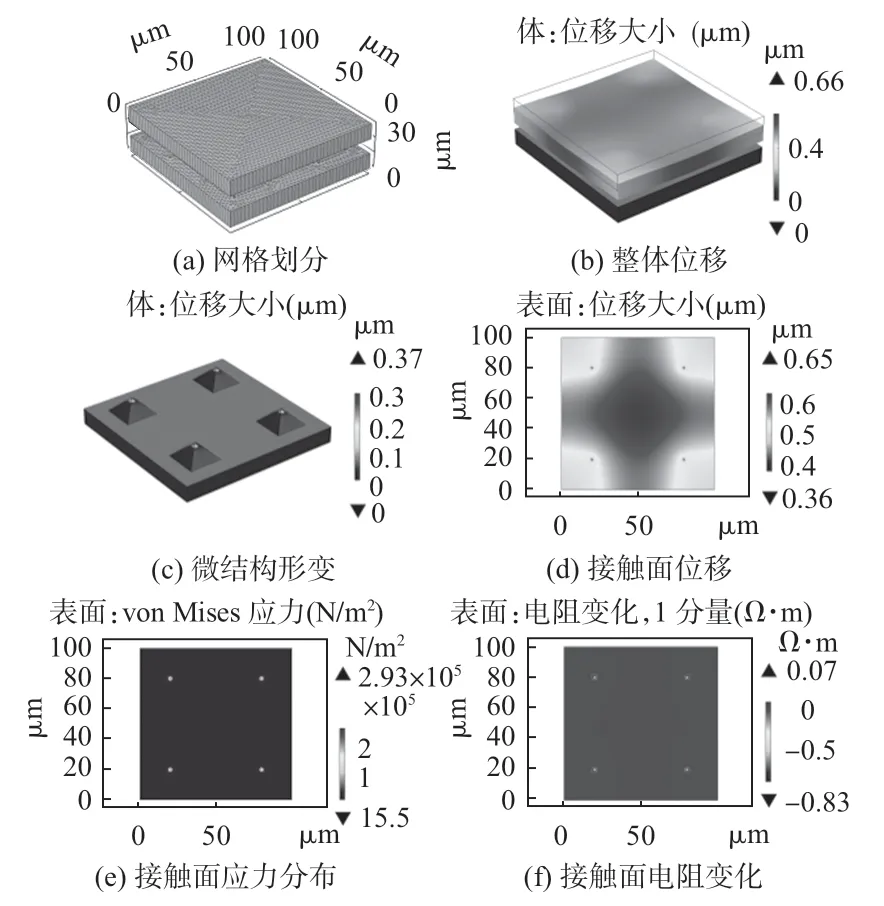
图10 金字塔压敏结构传感器仿真结果

3.4.5 半圆球压敏结构的传感器

图11为半圆球压敏结构的传感器在200 Pa 固定载荷下的仿真结果，图11（a）为传感器的网格划分，图11（b）～（d）所示仿真结果可知，传感器在受到外部正向载荷后，传感器的大部分区域都会向下位移。由于半圆球压敏结构的存在，且半圆球压敏结构和上层复合材料的接触面积非常小，导致接触面的应力非常集中，如图11（e）所示。这也导致了在半圆球微结构和上层复合材料的接触点附近区域的电阻变化非常大，但变化区域也非常集中，如图11（f）所示。

图11 半圆球形压敏结构传感器仿真结果

4 结 论

本文通过仿真模拟，分析了不同压敏结构对rGO／PDMS压阻传感器灵敏度增强作用。在确保仿真数据与文献数据吻合以及网格独立性验证后，再模拟传感器受到外部载荷后的变化，分析不同压敏结构的形变、接触面的位移、应力分布及电阻变化等。结果表明，压敏结构为方柱和圆柱时，在压敏结构与复合材料的接触面上电阻变化得到了提升，且变化区域较大。而压敏结构为金字塔和半圆球时，压敏结构与复合材料的接触面上电阻变化最为明显，但是电阻变化区域非常集中。综上可知，在压阻层构建压敏结构是提升柔性压力传感器灵敏度的重要方法。本文的仿真结果及分析为今后柔性压力传感器的设计与发展提供了参考，具有很好的实际意义。