重探物体的稳度

李亚磊 杨 浩 张思奥 孔令鑫 马帅奇 孙泽浩

(海军航空大学基础学院理化教研室,山东 烟台 264001)

2023年全国大学生物理实验大赛命题类题目1“不倒的杆”要求研究物体/装置的平衡原理,并制作一个能够帮助杆在风力等作用下稳定不倒的实验研究装置.杆件是最简单的刚体,研究其平衡问题具有简单、普适且实用的特点.如何提高杆件等刚体在风力等外部作用影响下的稳定性具有理论与现实意义.然而,目前人们对于物体的平衡稳定性与稳度的定义有不同的看法,[1-6]文献[1]认为应当用使物体倾倒所需要的功来描述稳度大小,也有观点认为可以用翻倒刚体所需的最小力矩与物重的比值来定义稳度,还有人认为应该以物体向某方向倾倒的最大倾斜角的正切函数值来定量描述物体稳度.[2]研究发现,上述对于物体稳度的定义多是从能量角度出发,并且都没有考虑地面摩擦力的影响.这些定义理论性较强且过于理想化,难以直接用来对杆件的稳定性进行实验研究.因此在本文中,笔者给出了一种刚体稳度的新的定义.新定义简洁明了并且更加符合生活实际情况.首先从理论出发,研究了刚体的平衡原理.给出了从一维到三维杆件的平衡条件以及影响其稳定性的因素.第二部分使用软件Algodoo进行仿真模拟,验证了二维理论中刚体稳度的影响因素.第三节以市面上常见的手机三角支架杆件为研究对象,测量了其尺寸、质量、摩擦因数等参数,并用第一部分的理论计算了其稳度,利用定滑轮和钩码模拟提供外力,实验验证了三维刚体的稳度与其重心高度无关.文章的最后给出了总结.

1 物体稳度的影响因素

从题目要求出发,研究杆在风力等作用下的稳定性.人们通常将物体在支撑面上保持平衡不易倾倒的能力称为稳度.生活经验和实验探究表明,当物体受到外界扰动后,物体可能会绕其与支撑面的接触点或接触线发生转动,这个点或线人们称为易倾点或易倾线.[1]当物体转动至重锤线超过易倾线时,此时即使撤去外界扰动,物体也会由于重力矩的作用发生倾倒.基于此,人们提出利用物体离开平衡位置到即将倾倒的临界状态时所需要的功来表示稳度.并且进一步得出初始平衡状态重力势能越小、倾倒临界状态重力势能越大,物体的稳定性越好.这也就是生活经验中常说的重心越低越稳定的理由.然而稍加分析不难发现,从能量的角度出发研究物体的稳定性存在不合理之处:一是由于常见物体的质量分布不均匀,难以确定其重心,从而也无法确定其重力势能;二是外界扰动的形式复杂多样,几乎不可能确定其做功的情况.生活中更加常见的现象是,外界对物体施加一个恒力,当力的大小超过某个值时,物体就会发生倾倒.例如研究非固定式的晾衣杆或广告牌在室外有风情况下的稳定性,可以将风力近似看作是分布均匀的恒力,风力的大小与风速有关.当风速超过某个值时,晾衣杆或广告牌就会发生倾倒.再例如手机三角支架受到人的误碰扰动发生倾倒的过程,由于扰动过程在时间和空间上都十分短暂,所以该过程支架受到人的推力也可视为恒力.因此不难理解,物体保持平衡时所能承受外力的值越大,物体的稳定性越好.接下来我们从一维刚体到三维刚体,逐步分析影响其稳度的因素有哪些.

由理论力学知识可知刚体平衡时必须满足下列平衡方程:

F=0,M=0.

(1)

即作用在刚体上诸外力的矢量和为0且诸外力对任一点的力矩的矢量和也为0.

首先研究一维情况.我们定义一维理想杆件为不计横向分布、仅有纵向长度的质量分布均匀的一维刚体.对于竖立在水平粗糙地面上的一维理想杆件来说,设其受到的水平风力等效作用点在杆的顶端,其受到重力、支持力、摩擦力和风力作用,如图1(a)图所示.

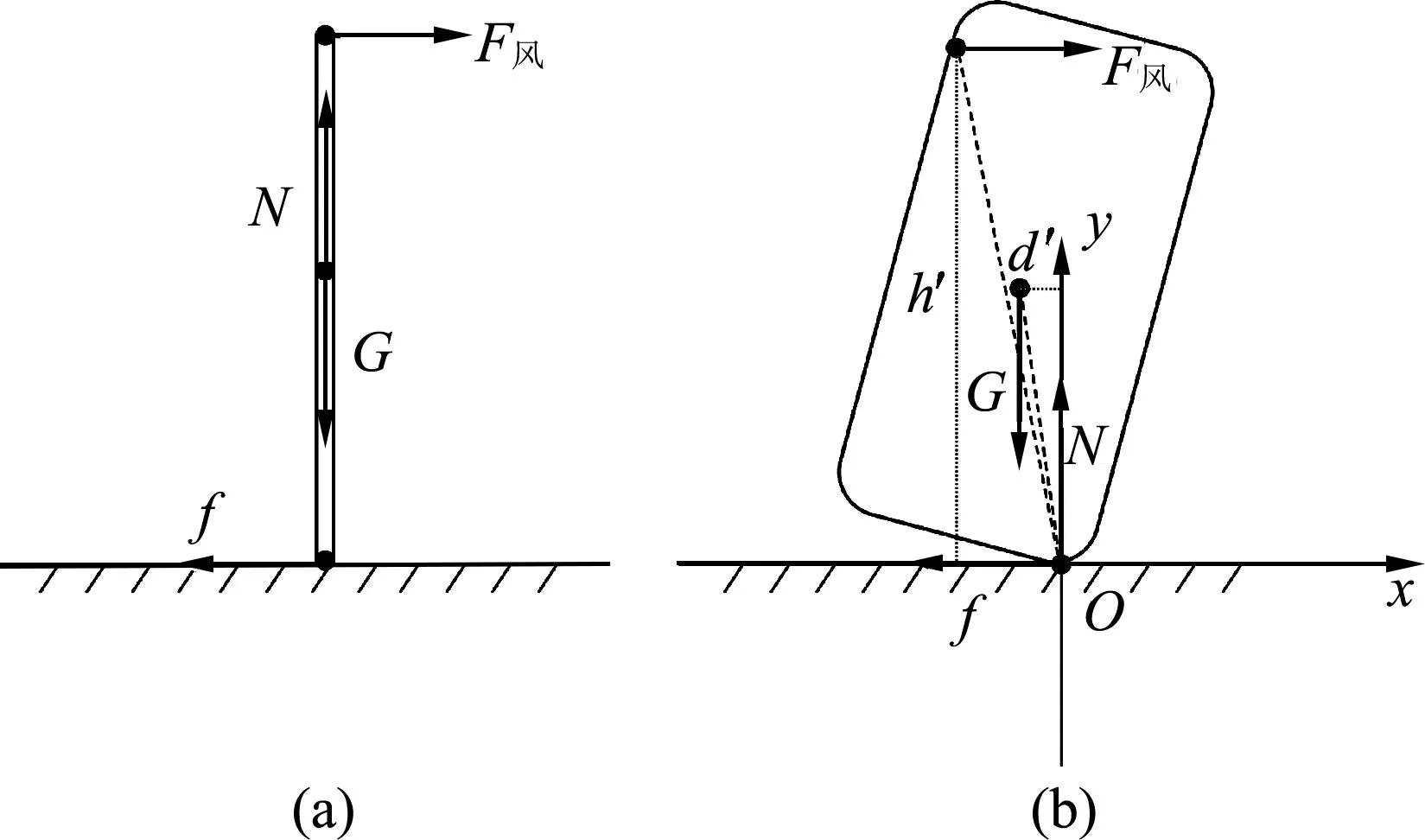
图1 一维和二维杆件的平衡受力

由平衡方程合外力为0的条件可得

N=G,F风=f.

(2)

由于重力、支持力、摩擦力的作用线均过接触点,它们对该点的力矩为0,故合外力矩仅由风力提供

M=F风l,

(3)

式中l为杆的长度.此即只要F风≠0,一维理想杆件就要受力矩作用发生转动,从而无法保持平衡.若风力作用点不在杆的顶端,区别仅在于风力的力臂减小,但力矩仍不为0.这就是说一维杆件的稳定性为0,只要存在外界扰动杆件就会倾倒.这和文献[2]的结论是一致的.

接下来考虑更加贴近实际的二维情况.对于高为h、宽为d、质量m分布均匀、质心与几何中心重合的二维理想刚体,当h≫d时可以认为该刚体是二维理想杆件.设杆在某一角度时处于平衡状态,此时受力情况如图1(b)所示(为方便示意,杆件的高宽比做了夸张处理).以杆件与地面的接触点,也即易倾点为坐标原点O,水平向右为x轴正方向建立坐标系.与一维情况类似,支持力和摩擦力的力矩为0,而重力提供的垂直纸面向外的力矩克服风力施加的垂直纸面向内的力矩,以使杆件保持平衡.设风力作用点位置距离地面垂直高度为h′,重心与y轴的距离为d′.合外力矩为零的平衡条件给出

F风h′=Gd′.

(4)

若此时风力增大或作用高度变高使得F风h′>Gd′,杆件将失去平衡发生转动,从而稳定性被破坏.

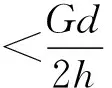
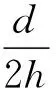
综合以上分析可以得出,杆件所能抵抗的最大风力与风力作用高度成反比,与物体的重力和倾距成正比.一般来说,生活中的风力与所处高度和风速有关,高度越高、风速越大,风力越强.但是总可以利用理论计算和经验公式,将风力等效为作用于杆件的某一点上.除此之外,对于其他类型的外界扰动也可以较容易地知道力的大小与作用高度.进一步地,物体的高度越高,外力可能的作用点也就越高,其提供的外力矩也就越大,也就越容易使物体发生倾倒.因此将位于水平面上物体的稳度定义为物体保持平衡不发生倾倒时物体顶部所能承受的最大外力,其大小等于物体的重力乘以物体倾距与高度的比值.需要强调的是该定义与文献[2]用最大倾斜角的正切值定义的区别.首先,文献[2]认为稳度不应当与物体重力有关.但是生活经验告诉我们,一个装满水的杯子的稳定性显然要比一个空杯子好.其次,文献[2]对稳度的定义是倾距与重心高度的比值,其论据是在重心处施加外力可以使物体绕倾点发生匀速转动,说明物体的稳定性被破坏.但从前述分析中可以看到,要使物体可以发生转动,必须要施加一个大于Gd′的力矩,而这个力才是衡量物体稳定性是否被破坏的量.可以看到,我们给出的新定义与生活实际更加相符,并且简洁明了,易于从实验上获得.值得注意的是,该定义下物体的稳度与且仅与物体的重力、高度和倾距有关,与物体的重心高度无关.将通过第二部分的仿真模拟和第三部分的实验予以证实这一反直觉的结论.

对于真实的三维情况,以市面上常见的手机三角支架为例,对其进行了建模,分析了影响其稳度的因素.为方便表述,命名支架的主体部分长度为l,三条支撑腿的长度均为l1,主体部分和支撑脚的连接处到地面的垂直距离高度为h1,支架顶端距地面高度为l+h1.建模时忽略支架的手机座、调节伸缩旋钮、连接结构等次要因素,将其简化为如图2(a)所示的4根一维理想杆件的组合体.

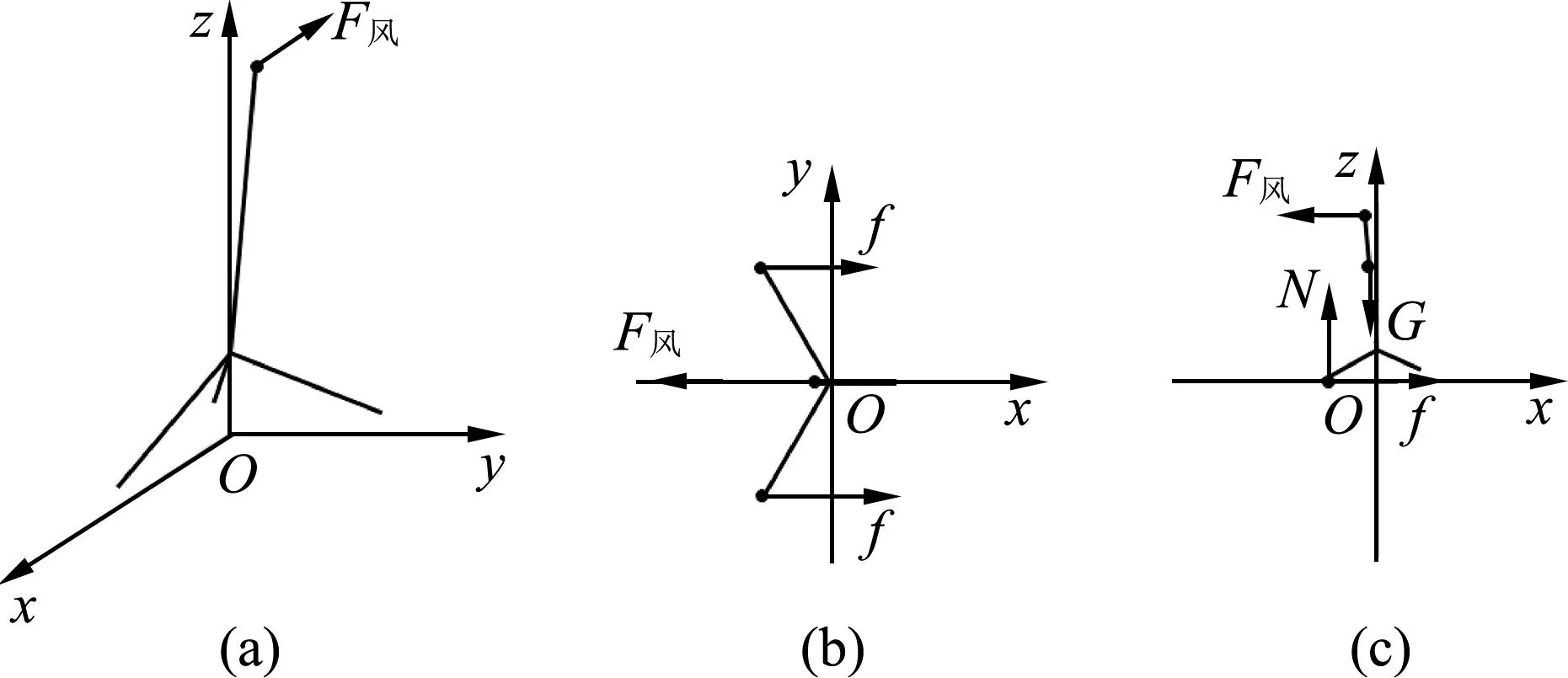
图2 手机三角支架模型的平衡受力

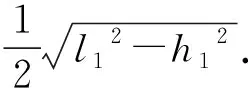
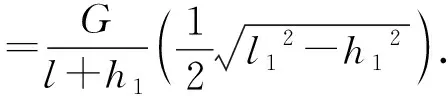
(5)

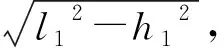
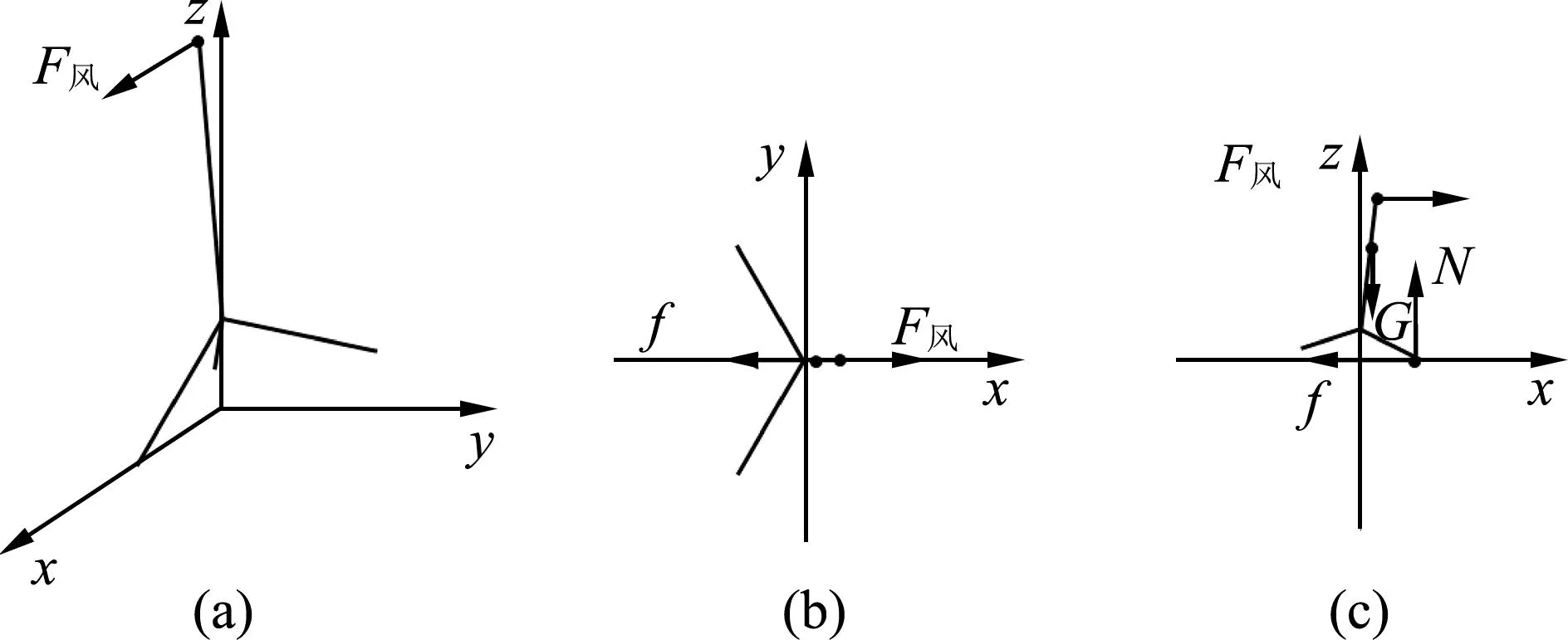
图3 风力沿x轴正向时的稳定性

综上所述,与二维情况类似,三维杆件的稳度仍为重力乘以倾矩和高度的比值,与重心高度无关.并且还可以得出的结论是,物体的稳度具有方向性,原因是对于不同的易倾线有不同的倾距.这和文献[2]的观点也是相符的.

2 二维刚体的Algodoo仿真模拟

Algodoo是瑞典Algoryx Simulation AB公司开发的一款仿真实验平台.它可以提供简单的二维情况下的力学与流体力学仿真模拟. 它的安装包大小仅有41Mb,并且操作简单易上手,仿真效果良好,非常适合物理教学.接下来我们以它为工具,研究二维刚体受水平风力时的稳定性问题.

首先研究上一节中提出的稳定性与摩擦因数之间的关系.Algodoo可以自定义二维材料的体积、密度、摩擦因数、弹性等参数,如图4所示.制作一个高8 m、宽2 m、弹性为0的质量为1 kg的二维刚体.软件提供的风力为分布在全空间水平向右的恒力,它的大小与空气和物体的接触面积(长度)D有关,与风速v的一次方和二次方有关.我们采用风力的默认公式

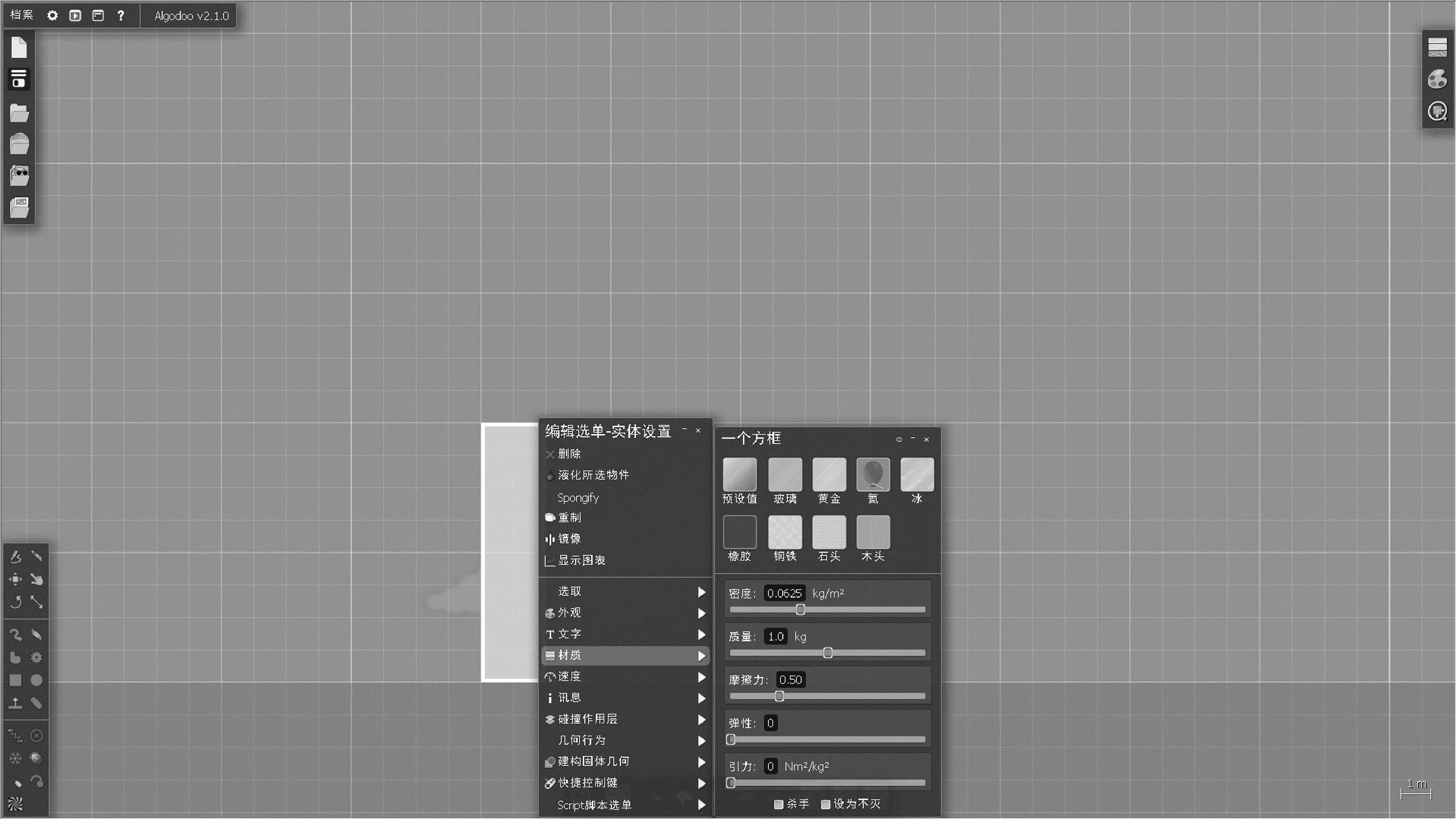
图4 应用Algodoo对二维刚体的建模

F=D(0.01v+0.001v2),

(6)

式中的v的一次项和二次项系数可以根据实际情况进行手动调整.

由于风力作用在全空间上,可以将其等效作用在刚体的中点h′=4 m处.此外由于刚体质量分布均匀,故倾距d′=1 m.通过第一节的分析可以计算得出杆件的倾倒临界摩擦因数μ=0.25,所能承受的最大风力为2.058 N,对应的最大风速为11.798 m/s.在仿真模拟中,设定风速大小为11.8 m/s,当摩擦因数大于0.25时,刚体发生倾倒;当摩擦因数小于0.25时,刚体只发生滑动而不会倾倒.分别改变刚体的高度、倾距、质量等参数,重复进行仿真实验,得到的倾倒临界摩擦因数和承受最大风速结果如表1所示.可以看到仿真实验结果与理论符合得很好.

表1 不同参数二维刚体的仿真实验结果

接下来探究二维刚体稳度与重心高度的关系.如图5所示,制作4个2 m×1 m相同体积的刚体A、B、C、D,其质量分别为0.1 kg、0.2 kg、0.3 kg、0.4 kg.将其彼此黏附在一起,并设定摩擦因数为0.5,以保证大于倾倒临界摩擦因数使其能倾倒.然后将其复制,按照D、C、B、A的顺序由上到下排放.显然后者的重心高度要高于前者.生活经验告诉我们后者的稳定性要较前者差,应当更容易被风吹倒.但是按照我们第一部分的理论分析二者的稳度是一样的.通过仿真实验发现,二者在风速小于7.8 m/s时都处于稳定状态,当风速大于7.8 m/s时同时发生倾倒.这与表1的结果是一致的.区别仅在于重心高的物体由于重力矩大,从而倾倒的速度更快.这一实验结果是反直觉且有趣的.

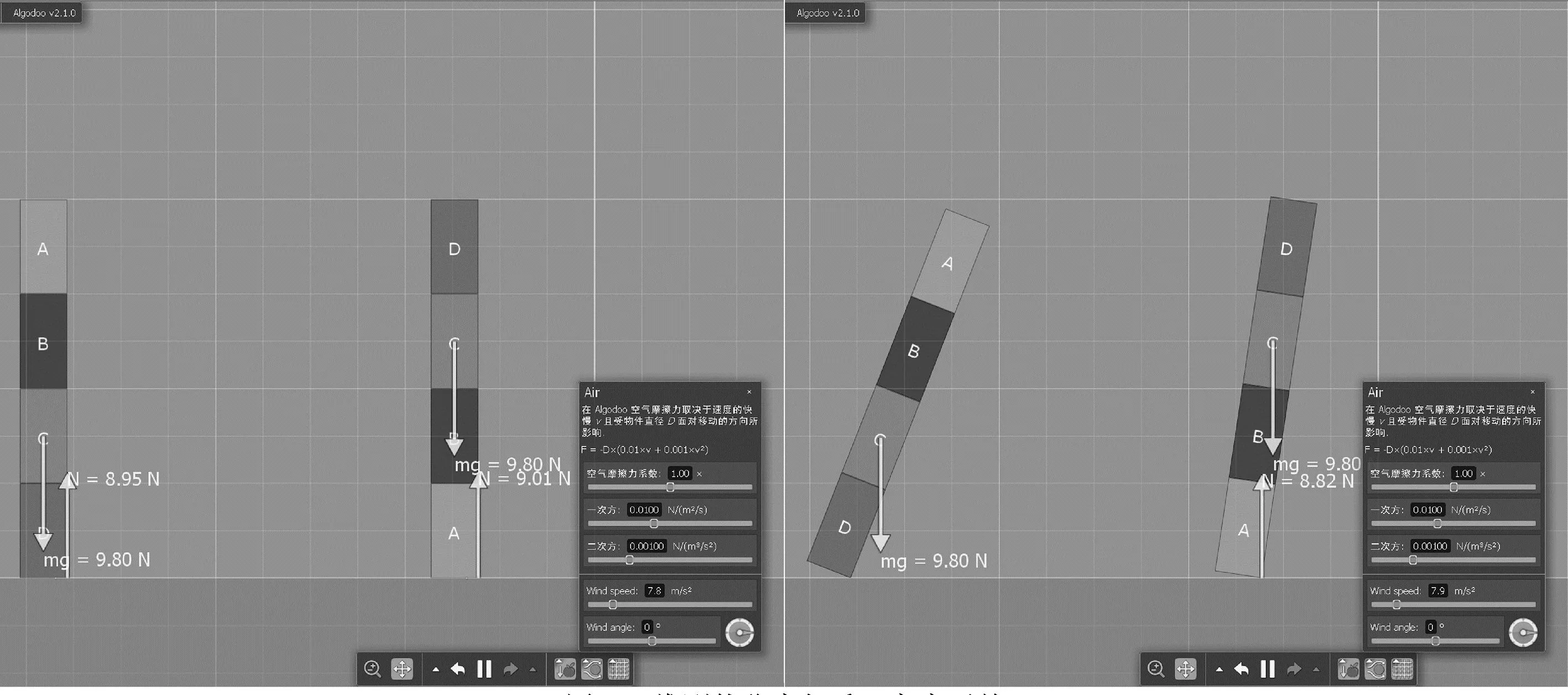
图5 二维刚体稳度与重心高度无关

综上所述,使用Algodoo进行仿真模拟,验证了二维刚体的倾倒临界摩擦因数和稳度的影响因素.证实了二维刚体受恒定风力时的稳定性与刚体重心高度无关.

3 手机三角支架稳度的实验测量

笔者购买了市面上常见的手机三角支架,实物如图6所示.测量获得其质量m=0.72 kg,支撑腿长度l1=32.28 cm,支架与瓷砖间的摩擦因数为0.27,主体部分长度l可根据需要在35.85～114.95 cm范围内调节,支撑腿连接处距支架地面垂直距离可根据需要在9.49～32.28 cm范围内调节.

图6 手机三角支架实物

为测量三角支架的稳度,我们将细线的一端系于支架的顶端,另一端通过定滑轮与钩码相连,利用水平仪保证细线提供的拉力沿水平方向,则钩码重力可近似认为是支架所受外力.根据第一节所述方法与定义,我们对支架的稳度进行了理论计算和实验测量,结果如表2所示.结果表明在误差范围内,实验结果与理论符合得很好.

表2 手机三角支架的稳度理论值与实验值对比

通过在支架的不同高度处固定配重可以调节重心,以验证支架稳度与重心高度的关系,实验结果如表3所示.

表3 手机三角支架的稳度与重心无关

由以上实验结果可以为我们带来启示:如果想要提高三角支架或是其他类似杆件的稳定性,也就是提升抗风、抗扰动、抗倾倒的能力,通过降低其重心的方法是不可行的,只能通过增加其重力、增大其倾距、减小其高度的方法.

4 总结

本文重探了物体稳度的定量描述与影响因素,给出了稳度新的定义方法,即物体保持平衡时顶端所能承受的最大恒外力,其等于物体的重力乘倾距与高度的比值.新的定义相较于以往的稳度定义,物理意义更加清晰,更易从实验获得,与实际应用联系更加紧密,更具理论与实践意义.利用Algodoo仿真模拟与真实实验,分别验证了二维和三维刚体稳度理论的正确性.证实了物体的稳定性与重心高度无关.这打破了长久以来人们的认识误区,为今后的物理教学与工程实践提供了理论指导.