黏性土中单桩基础桩基设计参数ε50 试验研究

王振红，蒯志要，赵梓鑫，葛建刚

（1.浙江华东岩土勘察设计研究院有限公司，浙江杭州 310014；2.中交第一航务工程勘察设计院有限公司，天津 300220）

引言

海上风机地基基础的安全可靠是保证风机长期安全运行的关键条件，也是影响海上风电场投资的重要因素。当风机基础采用单桩基础时，桩基轴向抗压、抗拔和水平向三个受力中，水平力属于控制性因素，为承载力设计的主要考虑因素，很多研究人员对水平荷载下桩土相互作用问题进行了广泛研究[1-3]。桩基受力分析中，目前广泛采用能全面反映桩的工作性状的P-Y 曲线法，是目前计算水平承载力较好的使用方法[4]，其涉及的土体参数主要有土体的有效重度、砂性土内摩擦角和黏性土不排水剪切强度及ε50值。在海上风电场建设中，黏性土是最常见的影响风机基础设计和风机运营安全的土类之一。在黏性土中，ε50是确定单桩在循环荷载作用下土体对桩的侧向抗力和侧向位移曲线的关键参数之一。而ε50参数的取值目前主要依据黏性土不固结不排水剪切试验（UU）成果读取，并进行相关的数理统计，推荐使用，人为因素影响大。海上风电场设计时ε50值与港口工程设计中的ε50的经验取值存在不同，目前尚缺少丰富的经验。因此，对ε50取值进行分析研究，对海上风机基础设计具有现实意义。

2 研究原理

2.1 土的结构性

很多试验资料表明，土的组成和土的物理状态不是决定土的性质的全部因素，土的结构对土的性质也存在很大影响。

黏性土中的黏土颗粒间重力作用较小，其主要由范德华力、库仑力、胶结作用力和毛细压力等粒间力起主导作用，细粒土的天然结构就是在沉积环境下受这些力的共同作用而形成的。沉积环境的不同也会导致结构的不同，以海洋环境为例，当细颗粒在海水中沉积时，海水中的大量的阳离子会导致土颗粒间斥力减少而应力增加，容易形成以角、边与面或边与边搭接的排列形式，称为片架结构[5]。

2.2 土的力学特性

1）土的弹塑性理论模型

土的弹塑性模型是建立在弹性理论和塑性增量理论基础之上的，它将土的应变分为可恢复的弹性应变和不可恢复的塑性应变，并分别用弹性理论和塑性增量理论计算。它包括破坏准则、硬化规律、流动法则三部分内容，对这三部分内容的假定不同，就形成了许多不同的本构模型理论[6]。

2）土的应力应变关系

土既不是理想的弹性材料，也不是理想的塑性材料，而是一种弹塑性材料。土在受应力作用时，弹性变形和塑性变形几乎会同时发生。如图1 为三轴压缩试验中土的应力应变关系曲线，曲线①表示理想的弹塑性体，曲线②表示超固结土或密实砂土的应力-应变关系曲线，曲线③则便是正常固结土或松砂的应力-应变关系曲线。与理想的弹塑性材料相比，土的形状与性质都存在很大的差异。

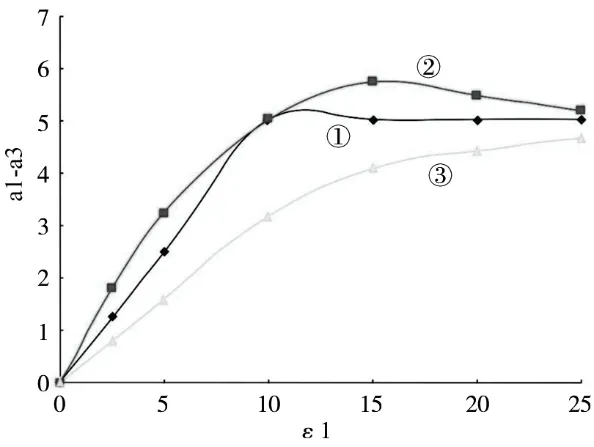
图1 土应力应变关系曲线Fig.1 The stress-strain curves of soil

3 试验内容及成果

3.1 试验内容

1）试验土样

本次试验使用土样来源为江苏某海上风电场区，主要为浅层的粉质黏土层，灰色，含少量贝壳碎屑、腐殖质。现场使用薄壁取土器取样，蜡封，并封装在专用的样品箱内，运输过程中减少震动，尽量减少对土样的扰动。

对采取的原状土样进行室内试验，得出其主要物理指标如下表1。

表1 土层物理力学性质统计成果表Tab.1 The physical and mechanical properties of soil stratum

从表1 中可以看出，试验土样主要为软塑～可塑的粉质黏土，其埋深一般为5～20 m，层厚1.30～9.50 m。

2）试验原理

规范中三轴UU 试验步骤首先是1 组试样在不排水条件下直接受不同围压σ3i（i=1，2，3，4）作用，然后在不排水条件下进行剪切[7]。对于饱和试样，在不排水条件下，围压σ3i将全部成为孔隙水压力，因此，试样都是在有效围压σ3’=0 的条件下进行剪切，这与试样在地下一定深度受力剪切的条件有明显差别。因为试样剪切前都处于超固结状态，剪切过程中将产生体积膨胀而使孔隙水压力低，因此试样都有一定的抗剪强度，这种机理形成的抗剪强度与固结应力产生的抗剪强度不同。土力学教科书中建议的方法则是先施加各向相等的初始固结应力σ0来模拟现场地基中土体所受的固结作用，然后在不排水条件下施加围压增量Δσ3和剪切应力，试样抗剪强度是由初始固结应力σ0产生的，这与现场不排水条件下的地基破坏机理是一致的。与三轴固结排水剪试验（CU）在固结时允许排水不同，三轴UU 试验施加初始固结应力进行预固结时一般不允许排水。

3）试验方法

根据规范与教科书中对试验方法描述的差异，对试验进行设计，原状样开样后可制备6 个样品，分a、b 两组。a 组按规范方法直接进行三轴不排水不固结剪切试验，取围压P1、P2、P3分别为100 kPa、200 kPa、300 kPa。b 组先进行k0应力状态预固结后再进行试验(k0为静止侧压力系数，小于1)。对于正常固结土，土体所受固结应力竖直向自重应力σs，水平方向等于 k0σs，试验使用样品均为正常固结土，本次试验k0取0.7，σs可根据样品埋深与上覆土层重度进行计算。样品经过约12 个小时的预固结后进行三轴不固结不排水剪切试验，取围压P1、P2、P3分别为100 kPa、200 kPa、300 kPa。

3.2 试验结果与试验分析

1）试验结果

本次共完成有效试验20 组，主要试验成果见下表2。

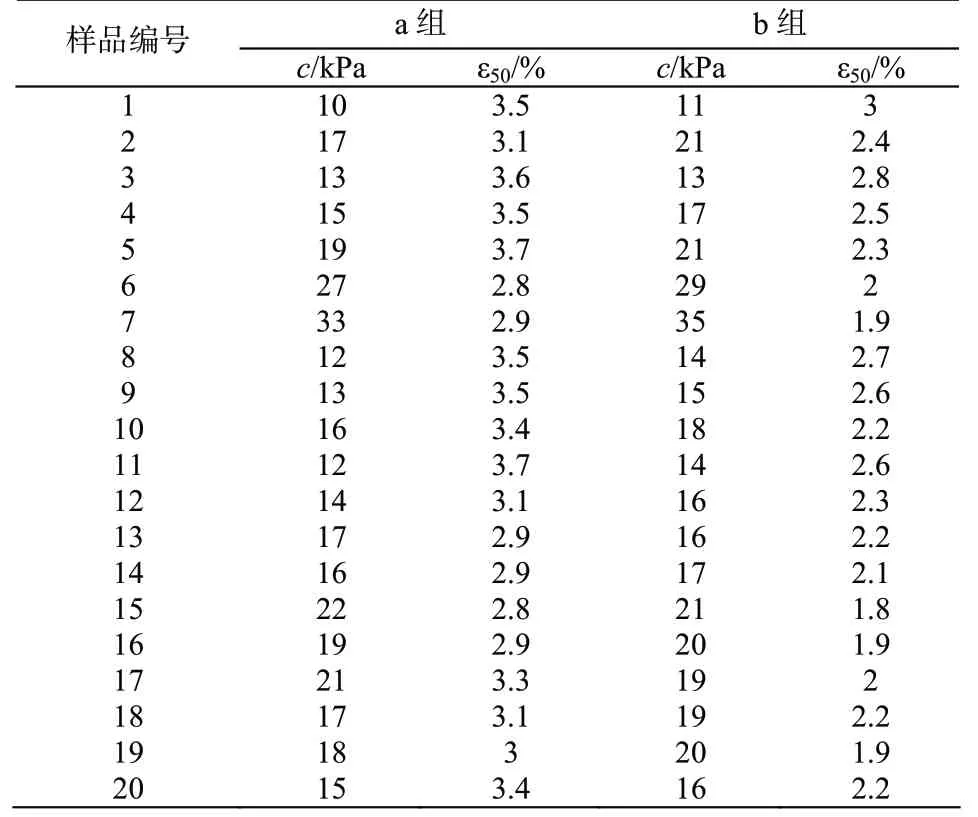
表2 UU 试验成果表Tab.2 The experimental results of UU test

从表2 中可以看出对试样进行预固结后再进行UU 试验，所得到的ε50明显变小，其结果与试桩反分析得到的ε50更加接近。ε50与抗剪强度也存在一定关系，抗剪强度c越大，其ε50越小。

2）试验结果分析

如图2、图3 为两组典型的三轴UU 试验应力应变关系曲线，a 组为未进行预固结试样的三轴UU试验应力应变关系曲线，b 组为预固结试样的三轴UU 试验应力应变关系曲线。从图中可以勘察，在初始阶段，轴向应变ε 较小时，随着轴向应变ε 增大，轴向主应力差Δσ（σ1-σ3）快速增大，此时土样变形主要为弹性变形，土样近似为弹性体；随后，土样进入屈服阶段，其变形模量减小，相同应变量内应力增量减小；土样变形量达到峰值后，应力达到最大，不再随应变增大而增大，试样发生破坏。

图2 第一组试样应力应变曲线图Fig.2 Stress-strain curve of the first group of specimens

图3 第二组试样应力应变曲线图Fig.3 Stress-strain curve of the second group of specimens

而图中a、b 组的差异主要集中在初始阶段：a组未预固结土样初始阶段，主应力差随应变变化速率小于b 组预固结后土样。这种差异使最终得出的ε50值出现差异。正如前文中提到的细粒土在天然状态下是以一定的结构存在的，而土样在原始土体中受到上覆应力及侧向应力的挤压。试样从地下取出后，取样——运输——开样过程中，其应力释放，试样中土粒结构会随之松散。试样进行预固结后再进行三轴UU 试验，能更好的模拟土样原始状态，得到的试验数据也相对更加准确。

抗剪强度c越大，ε50越小是由于抗剪强度c大的土样其土样中土粒排列更加紧密，土样压缩后，其轴向应力增速更快，也就使其轴向应力差在更小的变形量达到破坏强度时的一半。

3.3 试验方法探讨

某些文献中提到[8]，在进行三轴不排水不固结剪切试验前对土样预固结，在排水情况下进行。本次按照该方法进行了两组试验，试验结果如下 表3。

表3 预固结条件下三轴不固结不排水剪切试验结果Tab.3 Results of the triaxial unconsolidated undrained shear test under pre-consolidation conditions

从表3 中可以发现，土样抗剪强度c、ε50均变化明显。根据试验条件，认为对土样进行排水固结，使土样含水率发生变化，其得到的试验结果与真实结果存在一定偏差。且土样为黏性土，天然状态下可认为是隔水层，对其进行排水固结与原有天然状态不符，使试验结果失真。

3.4 与试桩反分析结果对比

根据预固结后三轴UU 试验得出的土体参数，按钢管桩水平受荷p-y 曲线法计算的各级水平荷载下桩身荷载-位移曲线与试桩成果的对比如图4。

图4 试验与试桩成果侧向抗力和侧向位移曲线对比Fig.4 Comparison of lateral resistance and lateral displacement curves between test and measured results

从图4 可见，在各级水平荷载下，根据室内试验数据得出的侧向抗力和侧向位移曲线与试桩反分析成果较为接近。

4 结语

1）ε50受土样结构性影响较大，土样的扰动很容易使试验数据发生失真。土样在取样、运输、开样过程中，要尽量减少扰动，以便得到相对准确的试验数据；

2）通过对20 组土样进行单变量差异化三轴UU 试验发现，ε50与抗剪强度c存在一定的关系，抗剪强度c越大，ε50越小；

3）预固结后再进行不排水不固结剪切试验（UU 试验）能更好的模拟试样原始状态，得出的试验结论与试桩试验反分析成果更加接近；

4）排水情况下进行预固结，与黏性土的原有天然状态不符，试验结果失真；

5）后续生产研究中，建议在试验进行前，预先对土样进行预固结，以便得到精确的ε50值。