摩擦提升系统静张力比与防滑安全系数的探讨

杨 勇

昆明有色冶金设计研究院股份公司 云南昆明 650051

随着矿山建设规模和开采深度不断增大，多绳摩擦提升系统广泛运用于矿山井下与井上的竖向运输，多绳摩擦式提升机在矿山竖井提升中担负着重要的提升任务。行业对多绳摩擦提升系统的研究，主要集中在防滑问题上。为了保证摩擦式提升机在工作中不发生打滑现象，必须验算防滑安全系数，包括静防滑验算、动防滑验算和安全自动防滑验算[1]，并通过实际矿山项目的防滑验算，分析探讨具体防滑技术措施。钱壮壮[2]提出，为了提高多绳摩擦提升系统的防滑安全性能，可从弹性体动力学角度出发，对提升系统在紧急制动、启动加速控制方式、提升系统参数等方面的防滑安全展开深入的研究。Liu J W 等人[3]研究了多绳摩擦提升系统的摩擦特性，包括钢丝绳与摩擦轮之间的摩擦因数、滑动趋势等，以提高提升系统的防滑安全性。

为确保竖井摩擦提升系统工作的稳定性、高效性及安全性，系统防滑验算成为设计的重要环节。对竖井多绳摩擦提升系统的防滑计算，主要采用张力比滑动极限法、防滑安全系数法、紧急制动加速度法和相对参数法。后 3 种方法计算较复杂，当前我国采用的是张力比滑动极限法，经过多年的设计应用也证明了该方法是可行的。同时，这也是 GB 50215—2015《煤炭工业矿井设计规范》和 GB 50771—2012《有色金属采矿设计规范》等中推荐的方法[4-7]。本研究基于防滑验算的基础理论和已有系统欧拉系数不变的特点，分析推导了满足安全规程要求的张力比值与欧拉系数的关系式，并给出了满足安全规程要求的设定值，便于判断已有摩擦提升钢丝绳的安全系数是否符合要求。

1 防滑验算的理论基础

张力比滑动极限法的理论依据是欧拉公式。钢丝绳与驱动轮间的受力如图1 所示。dl表示微段钢丝绳长度，dN表示钢丝绳对轮体的正压力，dF表示摩擦力，f为钢丝绳与驱动轮间的摩擦因数，α为钢丝绳在驱动轮上的包角。微段钢丝绳的一端拉力为F，另一端的拉力为F+dF；微段钢丝绳与驱动轮间的摩擦力为fdN。

图1 钢丝绳与驱动轮间的受力分析Fig.1 Stress analysis between wire rope and driving wheel

由静力学平衡方程可得

假设钢丝绳处在临界状态，即受到的最大静摩擦力dFmax=fdN，所以补充方程

同样 dα是一个小角度，所以，可得

联立方程 (2)、(4) 可得

对式 (5) 两边积分，

式中：F1为转动轮一侧的拉力；F2为转动轮另一侧的拉力，(F1＞F2)；eμα为欧拉系数，e为自然对数的底，e=2.718 28；μ为钢丝绳和驱动轮衬垫间的摩擦因数。

从式 (7) 可以看出，转动轮两侧的张力比是绳系在转动轮上是否发生滑动的前提条件。当张力比为1，即转动轮两侧拉力相同时，不管μ和α两个参数数值多小，系统在静止和匀速状态下，都不会发生滑移现象；反之，张力比大时，可以通过改变μ和α的大小来防止滑动问题，如索道驱动缠绕。

实际工程设计中，α由提升系统中摩擦轮和天轮(导向轮) 的几何位置决定，一旦系统形成，包角的大小也就确定；μ则是摩擦衬垫的材质、表面状态、压力和温度、润滑条件、使用环境等多种因素综合作用的结果[8-10]，设计计算时一般取 0.20 或 0.25。可见，这两个参数的数值，在设计阶段理论上已确定，计算过程中不会改变。

不同国家对摩擦系统的静张力比有不同的规定。比如，美国和加拿大规定静张力比不大于 1.4，苏联和德国规定静张力比不大于 1.5，英国则规定静张力比不大于 1.6；在我国，GB 16423—2020《金属非金属矿山安全规程》中规定，重载侧和空载侧的静张力比应小于 1.5[11]51。

2 静防滑安全系数与张力比的关系

根据 GB 16423—2020《金属非金属矿山安全规程》，钢丝绳静防滑安全系数是提升装置上钢丝绳打滑时的钢丝绳静张力差与提升装置钢丝绳实际最大静张力差的比值[11]6；钢丝绳静防滑安全系数应大于1.75[11]51。

静防滑安全系数

式中：Fjx为轻载侧钢丝绳的静张力，N；Fjs为重载侧钢丝绳的静张力，N。

工程设计中，Fjs=Fmax，Fjx=Fmin。将张力比设为k，k=Fmax/Fmin。式 (8) 可变化成

化简可得：

实际工程设计中，最大静张力比和欧拉系数是设计阶段给定的，而由此形成的满足规程静张力安全系数要求的区域如图2 所示。图2 中，区域 ①为滑动区域，区域 ② 不滑区域，区域 ③为满足安全规程区域，区域 ④ 为包角过大区域。当静防滑安全系数大于1.75 时，张力比和欧拉系数的常用值如表1 所列。

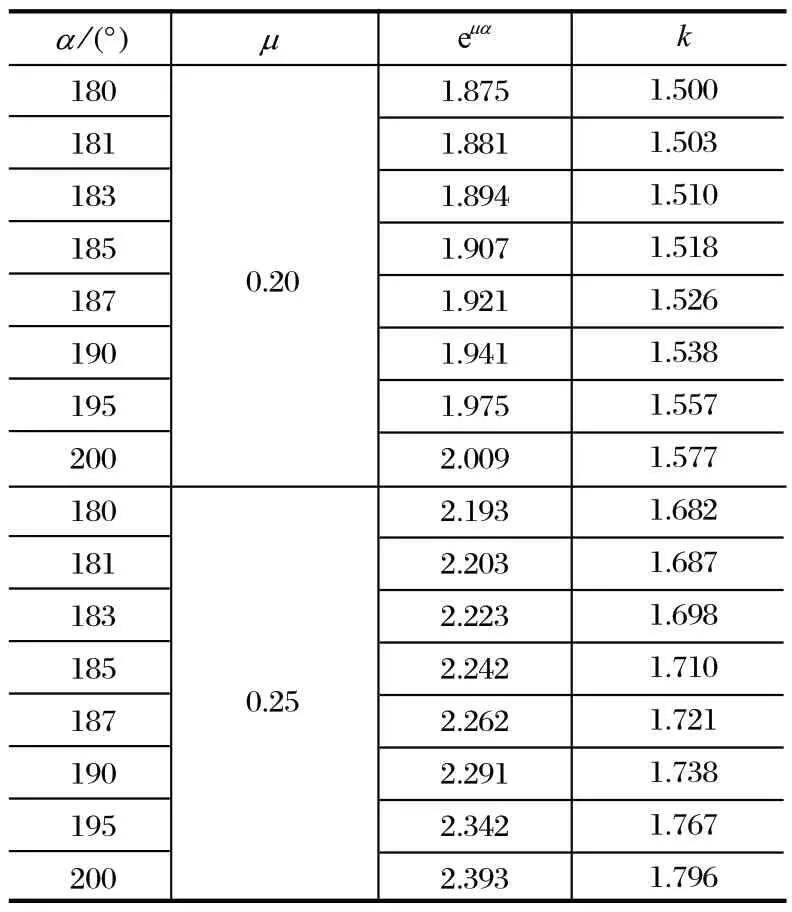
表1 与静防滑安全系数相关的，欧拉系数和张力比的常用值Tab.1 Common values of Euler coefficient and tension ratio related to static anti-skid safety coefficient

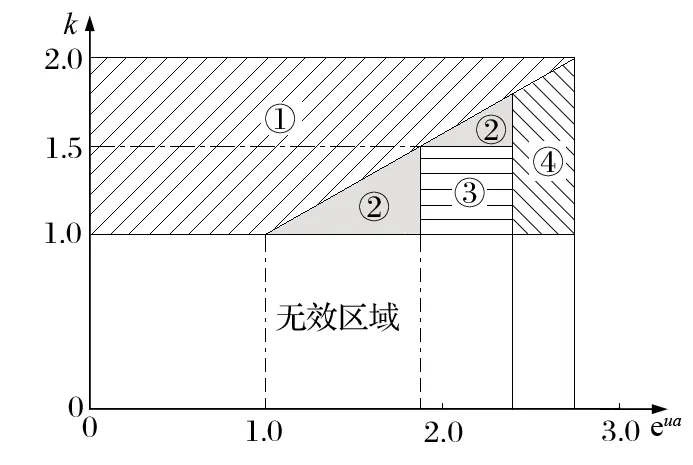
图2 张力比、欧拉系数与静防滑安全系数的关系Fig.2 Relationship between tension ratio、Euler coefficient and static anti-skid safety coefficient

通过图2 中各区域的位置关系，可以判断摩擦提升系统的静防滑安全系数是否满足安全规程中大于1.75 的要求。通过表1 和式 (11)，则可快速计算出系统的静防滑安全系数。同时，如果包角已知，k值若小于表1 中对应数据，则静防滑安全系数大于 1.75；k值在数据附近，则实际包角大于表中对应包角，静防滑安全系数也大于 1.75。

3 动防滑安全系数与张力比的关系

摩擦提升系统在加速和减速运动状态，最易发生钢丝绳滑动现象，因而摩擦提升系统不仅要进行静防滑安全系数校核，还需对动防滑安全系数进行校核。

根据 GB 16423—2020《金属非金属矿山安全规程》，钢丝绳动防滑安全系数是提升系统加速或减速运行过程中，提升装置上钢丝绳打滑时的钢丝绳张力差与提升装置钢丝绳实际最大动张力差的比值[11]6；动防滑安全系数应大于 1.25[11]51。

动防滑安全系数

式中：Fs为上行 (重载侧) 钢丝绳的动张力，N；Fx为下行 (轻载侧) 钢丝绳的动张力，N；ms为上行侧的运动质量，kg；mx为下行侧的运动质量，kg；Gd为导向轮的变位质量，kg；R为提升容器在井筒中的运行阻力，kg，双箕斗取 0.15Q，双罐笼取 0.2Q，其中Q是有效装载量；a为提升加速度，m/s2。

GB 16423—2020《金属非金属矿山安全规程》规定[11]49：竖井升降人员时，加速度和减速度不应超过 0.75 m/s2；升降物料时，加速度和减速度不应超过 1.0 m/s2。计算时取大值 1.0 m/s2。

将式 (13)～(16) 代入式 (12)，可变形为

略去Gd和R的影响因素，式 (17) 可简化为

将a=1.0 (m/s2)，g=10 (m/s2)，k=Fjs/Fjx代入式 (18) 可得：

实际工程设计中，由于最大动张力比和欧拉系数是设计阶段给定的，由此形成的满足规程动张力安全系数要求的区域如图3 所示。图3 中，区域 ①为滑动区域，区域 ② 不滑区域，区域 ③为满足安全规程区域，区域 ④ 为包角过大区域。a=1.0 m/s2，动防滑安全系数大于 1.25 时，张力比和欧拉系数的常用数值如表2 所列。

表2 与动防滑安全系数相关的，张力比与欧拉系数的常用值Tab.2 Common values of tension ratio and Euler coefficient related to dynamie anti-skid safety coefficient

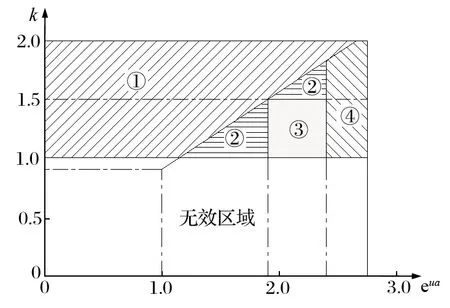
图3 张力比、欧拉系数与动防滑安全系数的关系Fig.3 Relationship between tension ratio、Euler coefficient and dynamic anti-skid safety coefficient

通过区域位置关系，可以判断摩擦提升系统的动防滑安全系数满足安全规程中大于 1.25 的要求；通过表1 和式 (20)，则可快速计算出系统的动防滑安全系数。同时，如果包角已知，k值小于对应表格数据，则动防滑安全系数大于 1.25；k值在表格数据附近，则包角大于对应包角，动防滑安全系数也大于1.25。

4 结语

摩擦提升系统一般都处在矿山运输环节的“咽喉”部位，同时系统相对速度较快、工况复杂，其工作性能的稳定性、高效性及安全性是决定矿山工作任务完成和生产安全的关键因素。因此，摩擦提升系统的防滑不仅在设计、调试阶段要按规程、规范设置和验收，而且在使用过程中，采用张力检测装置的数据、实时加速度数据、首尾绳参数、箕斗运行位置参数、提升系统几何参数等，计算出实际张力比，结合计算的欧拉系数，确保系统工作点处于不滑区域或满足安全规程区域内，系统运行时不会发生打滑现象。如果将此对比引入提升控制系统，可随时监控实际张力比数值与满足安全规程要求张力比数值的关系，临近状态时给出提醒信号，超出则自动降低加速度或者停止运行。对标规程给定的数值，通过提升机制动系统的液压站、控制柜、制动装置及提升机运行状态整体考虑，可实现基于监测数据的故障诊断与报警、参数修改和数据查询等功能，确保系统随时处在安全的运行状态。