竖井地面预注浆帷幕安全厚度研究及其在隧道通风井中应用——以天山胜利隧道4号通风竖井为例

毛锦波,赵红刚,韩 强,姬中奎,张斌斌,李亚隆

(1.中交二公局东萌工程有限公司,陕西 西安 710119; 2.中煤科工西安研究院(集团)有限公司,陕西 西安 710077)

0 引言

目前,在富水地层条件下进行地下工程施工时,通常采用高压注浆的方式将浆液注入工程周围地层的裂隙中,待浆液凝固后在井筒周围形成类似帷幕的防渗墙,从而达到堵水与稳固地层的目的[1-2]。注浆止水帷幕设计的关键在于确定合理的注浆帷幕厚度。

近年来,众多专家学者对注浆帷幕安全厚度进行了系统研究。刘志强等[3]通过构建立井井壁应变监测系统,并依据实测井壁的附加应变变化趋势来控制表土层注浆加固过程; 刘孝孔等[4]利用钻孔注浆试验手段,分析并优化了厚松散层主含水层的注浆技术参数,给出了适用于偏斜井筒变形的注浆加固技术; 付治安[5]针对沁城煤矿卵砾石地层涌水量较大的情况,设计了立井帷幕注浆止水方案; 周禹良等[6]为解决溶蚀孔隙型白云岩含水层竖井工程的水害问题,采用达西两相流理论得到了浆相有效扩散范围的计算方法;吴松锋等[7]通过流固耦合理论在厚壁圆筒模型基础上推导了隧道注浆帷幕力学模型,并对流固耦合作用下的隧道围岩位移与有效应力进行了研究; 朱明诚[8]针对含水流沙地层中立井施工困难这一情况,提出采用带压保浆法进行旋喷帷幕施工; 黄伟[9]通过壁后土层注浆加固理论,设计了荣康煤业立井帷幕注浆技术方案;张伟杰等[10]通过注浆模型试验讨论了帷幕注浆过程中富水破碎岩体的物理力学变化规律,并总结出针对渗透-劈裂型与微劈裂型2种界面的注浆加固模式; 林东才等[11]根据某煤矿立井井筒围岩力学特性和周围地下水的渗流机制,选用高分子注浆材料马丽散N对立井井筒进行注浆封堵; 袁东锋等[12]采用钻孔压水试验分析白云岩含水层溶蚀裂隙特征及浆液扩散规律,并给出了含水岩层井筒帷幕体的合理注浆参数。

可见,上述专家、学者从理论力学分析、现场测试和模型试验等方面对注浆帷幕进行了深入分析,所得的研究成果对注浆止水帷幕设计具有重要的参考价值。但实际工程中,注浆帷幕体的稳定性受开挖扰动、地层压力、孔隙水压、掘进段高、井筒直径及井壁暴露时间等众多因素的综合影响,其合理厚度的确定是一个复杂的计算分析过程。而以上文献较少考虑扰动作用以及含水层孔隙水压对竖井注浆帷幕体稳定性的影响。因此,本文以天山胜利隧道4号通风竖井为工程背景,考虑竖井开挖过程中的爆破扰动效应和孔隙水压作用,基于弹塑性力学理论,构建地层压力和孔隙水压共同作用下的注浆帷幕体力学计算模型,提出竖井注浆帷幕安全厚度理论计算公式,并确定了4号通风竖井注浆止水帷幕的合理安全厚度,取得了显著的注浆堵水效果。

1 竖井地面预注浆原理与方法

天山胜利隧道为高速公路隧道,全长22.105 km,共有4组通风竖井,其中4号竖井位于省道301乌斯特火车站以北8 km处,是天山胜利隧道的关键控制工程。根据现场勘察结论可知,竖井埋深为513 m,井筒周围为大理岩岩体破碎、节理裂隙较发育、透水性中等,4-1号竖井涌水量取7 062 m3/d,4-2号竖井涌水量取7 186 m3/d,地下水位埋深为128.60 m,高程为3 325.6 m,静止水位为47.76 m。

由于天山胜利隧道4号通风竖井所在地层基岩具有裂隙高度发育、富水的特性。为确保天山胜利隧道4号竖井的顺利掘进,在4-1和4-2号井井筒周边通过地面预注浆,对地下120～340 m的大理岩裂隙含水层进行注浆封堵,形成井筒帷幕体,在其保护下再进行井筒掘进。4号竖井开挖半径为5.65 m,考虑到浆液扩散半径要重叠0.5 m,因此每个井布置10个钻孔,如图1所示。其中,8个为注浆孔,2个为补查孔,每孔深350 m,预计总钻探进尺7 000 m。

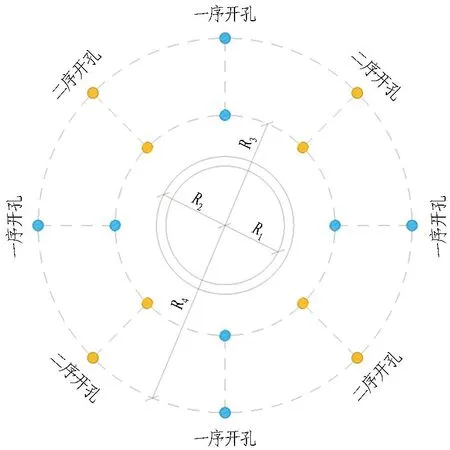
R1=4.5 m为井身净直径; R2=5.65 m为靶区内最大开挖半径; R3=9 m为开孔点直径; R4=15 m为靶区内直径。

8个钻孔均采用错位分段注浆法,如图2所示。钻孔的1开孔段为非注浆段(0～30 m),钻孔形式为直孔,钻至黏土、碎石及回填段以下2 m; 2开孔段为非注浆段(30～120 m),钻孔形式为定向孔,钻孔深度至地下水位以下1.4 m位置; 留20 m岩帽; 3开孔段为裸孔注浆段(140～340 m),段高为50 m,钻孔形式为导斜和直孔段,钻孔全部为裸孔,孔深至井筒底板以下17 m; 探测注浆段(340～530 m),根据探测情况确定是否延长其他钻孔。

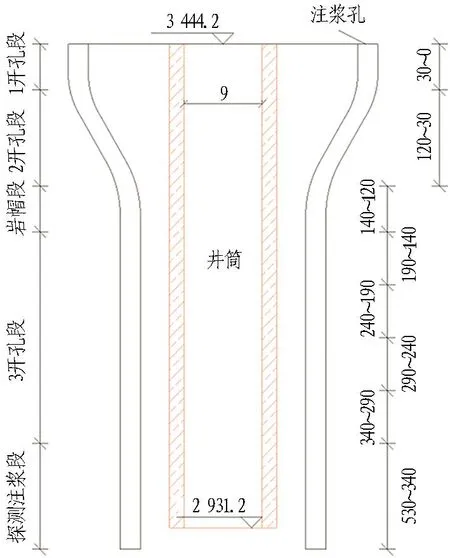
图2 钻孔剖面示意图(单位:m)

2 注浆帷幕力学模型假设与求解

2.1 竖井注浆帷幕厚度的构成分析

考虑竖井开挖过程中的爆破扰动效应,将竖井注浆帷幕厚度分为有效厚度和无效厚度2部分[4,11],如图3所示。

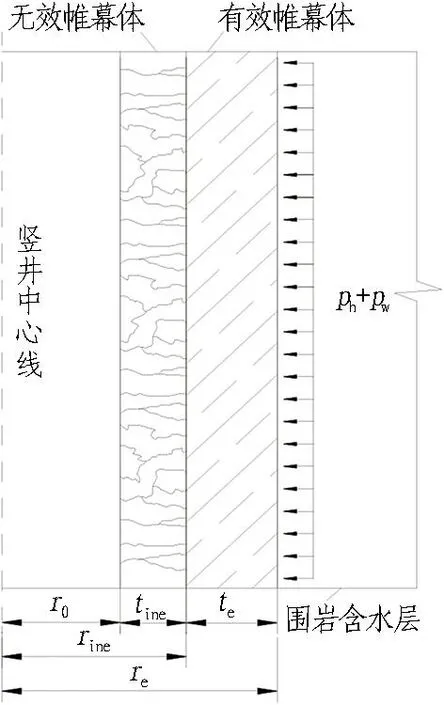
图3 竖井注浆帷幕体分析模型

竖井开挖后,r0为井筒荒径;rine、re分别为有效帷幕体内半径和外半径;ph为水平地层压力;pw为孔隙水压力。注浆帷幕体的无效厚度tine是竖井开挖爆破作用下注浆帷幕体一定范围内产生的粉碎带,不能起到有效的止水作用,tine=rine-r0; 注浆帷幕体的有效厚度te(te=re-rine)是指未受竖井开挖破坏、较为完整的隔水体,是防渗和维持井壁稳定的主体。

2.2 基本力学假设与力学模型

2.2.1 基本力学假设

为简化计算过程,根据有效帷幕体的受力变形特性,构建可解析求解的力学模型,现作出如下简化和假设:

1)考虑钻爆法施工对围岩的破坏作用,将爆破对围岩的扰动破坏区定义为塑性区,并以此为起点作为有效注浆帷幕体的弹性设计厚度内边界。

2)由于竖井纵向受力变化规律不符合平面应变的假设,但考虑到井筒开挖断面尺寸远小于井筒深度,以深部条件对有效帷幕体平面模型进行简化,实现保守力学分析。

3)将有效帷幕体外侧周边岩土体假设为连续的均质各向同性线弹性材料。

4)暂不考虑地下水的渗流耦合作用。

2.2.2 力学分析模型

在上述简化和假设的基础上,建立有效注浆帷幕体径向变形力学分析模型,如图4所示。L0为通风竖井井壁外边界;L1(r=rine)处为定点爆破后有效注浆帷幕体的内边界; 有效注浆帷幕体外边界L2(r=re)处作用的地层荷载为初始水平地应力ph与孔隙水压力pw之和。

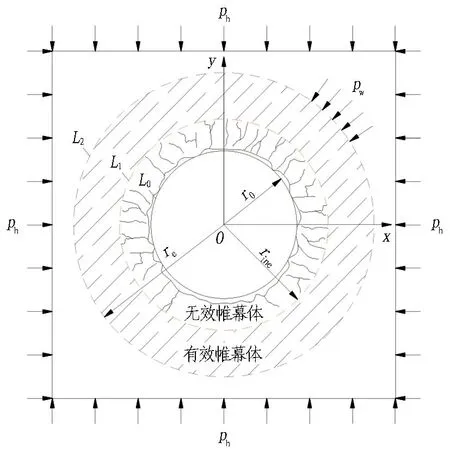
图4 有效注浆帷幕体力学分析模型

2.3 有效注浆帷幕体变形分析

根据上述基本假设,可将其视为轴对称平面应变问题。由弹塑性理论可知[13],有效注浆帷幕体的应力-应变关系为:

(1)

式中:εr、εθ分别为径向与环向应变;σr、εθ分别为径向与环向应力;ψ为有效注浆帷幕体弹性与塑性剪切模量的比值,ψ=Ge/Gp;Ge为有效注浆帷幕体弹性剪切模量,Ge=E/2(1+μ),MPa;Gp为有效注浆帷幕体塑性剪切模量,MPa。

根据有效帷幕体的应变几何方程:

(2)

式中:u为径向位移;r为注浆帷幕半径。对r求导得

(3)

将式(2)代入式(3)可得

(4)

将式(1)代入式(4)中可得

(5)

式(5)两边同时对r积分得

εθ=Jr-2。

(6)

式中J为积分常量。

联立式(1)和式(6)可得

(7)

在计算帷幕体径向位移时,考虑应力增量作用[11],将式(7)改写为:

(8)

在帷幕体弹塑性界面上有:

(9)

式中:p1为注浆帷幕体内边界的地层压力,MPa;c为有效注浆帷幕体的黏聚力,MPa;φ为有效注浆帷幕体的内摩擦角,(°);rp为有效注浆帷幕体塑性区半径,m,其大小为

(10)

将式(9)代入式(8),可得到积分常量J的表达式为:

(11)

由此可得有效注浆帷幕体径向位移为

(12)

则有效注浆帷幕体在弹塑性交界面处的径向位移为:

(13)

2.4 竖井注浆帷幕体安全厚度计算

2.4.1 注浆帷幕体无效厚度分析

竖井采用直孔掏槽爆破方法一次成井,其技术的关键在于能否破碎并抛出掏槽区域内的岩体。根据球状药包破岩理论可知,爆破时岩体将产生一定范围的破碎区,其半径为:

(14)

式中rb为炮孔设计半径。

则注浆帷幕体的无效厚度可表示为:

(15)

2.4.2 注浆帷幕有效厚度的确定

竖井注浆有效帷幕体主要承受水平地层压力与含水层的孔隙水压。由于有效帷幕体未受到施工扰动破坏,可将其视为均质、连续且各向同性的弹塑性体。取单位高度有效帷幕体为研究对象,根据厚壁圆筒理论[16]可得有效帷幕体中任一单元体的弹性径向位移为:

(16)

式中:μ为帷幕体泊松比;Gs为帷幕体剪切模量。

由式(16)可得有效帷幕体弹塑性交界面(r=rp)处的弹性径向位移为:

(17)

由帷幕体外壁围岩和有效帷幕体的位移协调条件可知:

(18)

联立式(13)、式(17)及式(18)可得:

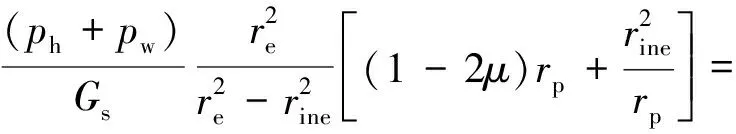
(19)

由式(15)及式(19)得注浆有效帷幕体外半径re,则注浆帷幕体的有效厚度te与安全厚度ts分别为:

(20)

3 注浆有效帷幕体稳定性分析

3.1 有效帷幕体横向稳定性验算

根据上述理论计算出注浆帷幕体的安全厚度后,还需对注浆有效帷幕圆环进行稳定性验算。为了保证有效帷幕体的横向稳定,要求其长细比满足:

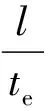
(21)

式中:l为有效帷幕圆环换算长度,l=1.814rav,其中,rav为有效帷幕圆环内、外平均半径,rav=(re+rine)/2。

取单位高度的帷幕圆环为研究对象,根据平面应变理论进行分析。当帷幕圆环失去横向稳定性时,均匀径向临界压力

(22)

式中:E为帷幕体的弹性模量;I为注浆帷幕圆环的纵截面惯性矩,I=bh3/12(b为注浆帷幕的厚度;h为注浆帷幕高度)。

(23)

要求满足:

(24)

式中vk为稳定性计算安全系数,vk=1.3。

3.2 注浆帷幕体强度验算

通常注浆有效帷幕体的厚度满足te≥0.1r0[17],在有效帷幕体受均匀侧向压力条件下可按照厚壁圆筒理论来验算有效帷幕体的强度,如图5所示。

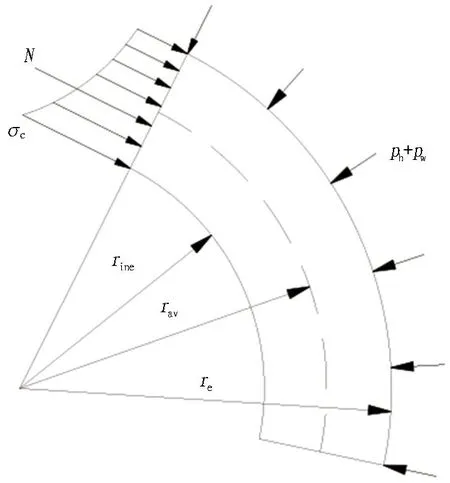
图5 注浆帷幕体横截面轴力分布

有效帷幕圆环截面轴向力大小为:

N=(ph+pw)re。

(25)

帷幕圆环截面上的最大计算主应力σc在有效帷幕体内侧为

(26)

式中fc为注浆帷幕体的抗压强度设计值。

4 隧道通风竖井工程应用分析

4.1 注浆帷幕体安全厚度的确定

根据现场测试结果可知,有效注浆帷幕体的基本物理力学参数如表1所示。

表1 有效注浆帷幕体物理力学参数

由表1可知,有效注浆帷幕体弹性剪切模量Ge=3.28 GPa; 帷幕体所受水平地层压力ph=4.55 MPa; 作用在帷幕体外侧曲面上的孔隙水压力pw=3.09 MPa。

4.1.1 注浆帷幕体无效厚度计算

将上述基本参数代入式(14)可得竖井围岩粉碎区半径为:

6.175 m。

(27)

则注浆帷幕体的无效厚度为:

tine=6.175-5.65=0.525 m。

(28)

4.1.2 有效帷幕体内侧径向位移的计算

有效注浆帷幕体塑性区半径可由式(10)计算得到:

(29)

将上述基本物理力学参数代入式(12)得到有效帷幕体内侧(r=rine)的径向位移为

8.55 mm。

(30)

4.1.3 注浆帷幕体有效厚度的确定

将上述基本物理力学参数代入式(19)中,借助MATLAB数学软件进行计算得注浆帷幕体外径re=12.146 m。可求得注浆帷幕体的有效厚度为:

te=12.146-6.175=5.971 m。

(31)

由式(20)可得注浆帷幕体的理论安全厚度为:

ts=12.146-5.65=6.496 m。

(32)

4.2 竖井注浆帷幕体的稳定性验算

4.2.1 横向稳定性验算

按照求得的注浆帷幕安全厚度可知,帷幕体外半径re=6.496 m+5.65 m=12.146 m。注浆有效帷幕圆环内、外平均半径rav=(12.146 m+6.175 m)/2=9.16 m,其长细比为:

(33)

满足长细比基本条件。

选择单位高度的帷幕圆环,由式(24)得帷幕圆环失稳时的临界压力为:

1.3×(4.55+3.09)=9.93 MPa。

(34)

满足注浆帷幕体的横向稳定性条件。

4.2.2 强度验算

将注浆帷幕体的基本物理力学参数代入式(26)得有效帷幕圆环截面内侧的最大计算主应力为:

(35)

由式(35)可知,注浆帷幕体满足强度设计条件。综上所述,确定注浆帷幕体安全厚度取为6.5 m。

5 通风竖井地面预注浆堵水效果分析

5.1 注浆效果物探检验分析

为验证竖井地面预加固实施效果,现场采取孔间CT和孔内电视相结合的方法对注浆堵水效果进行综合评价。

5.1.1 孔间CT法

对4111-4112、4112-4122、4122-4114、4114-4111检查孔开展跨孔电阻率CT工作,测试成果如图6所示。测试结果表明,钻孔之间的岩体电阻率整体较高,岩体完整性好,一般为9 000～30 000 Ω·m。图中圈出的局部低阻异常区电阻率普遍为3 000 Ω·m左右,远高于裂隙充水时的大理岩层电阻率(一般<1 000 Ω·m)。推测该处为注浆充填后的破碎大理岩区域,也间接反映注浆治理段注浆效果良好。

图6 4-1竖井注浆孔孔间CT测试结果

5.1.2 孔内电视法

通过41B1和41B2检查孔对注浆治理段岩层进行钻孔成像,观察岩体完整性、有无残余裂隙及注浆充填效果,如图7所示。检查孔孔壁光滑,无明显裂隙,局部明显可见原地层裂隙被浆液充填密实,无残余裂隙,注浆充填效果良好。

(a) 41B1检查孔

5.2 注浆帷幕体稳定性监测与分析

为验证该注浆帷幕体安全厚度的合理性,确保注浆帷幕体稳定,对竖井井壁应力及其位移进行监测与分析。

5.2.1 井壁应力监测分析

通过地面预注浆过程中钻孔之间的串浆现象和施工现场钻孔取芯结果分析,浆液实际扩散半径大于6.5 m,浆液能够在井壁周围形成较为完整的注浆帷幕体。整个注浆加固施工过程中,各监测层位井壁应力实测值如图8所示。

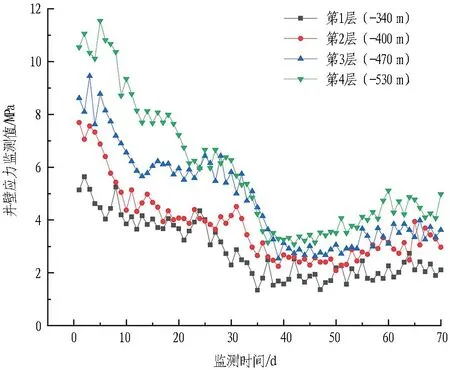
图8 井壁应力变化实测结果

监测数据表明,70 d内4个水平中段的井壁应力变化相似。井壁最大应力值为11.54 MPa,出现在-530 m水平中段断层带。0～40 d各监测层位井壁应力整体随监测时间逐渐减小,井壁应力实测值在40～70 d时在一定范围内趋于稳定。这一现象反映出通过地面预注浆法所形成的竖井注浆帷幕对地下水具有良好的封堵作用。

5.2.2 井壁位移监测分析

井壁随深度变化的累计位移曲线见图9。

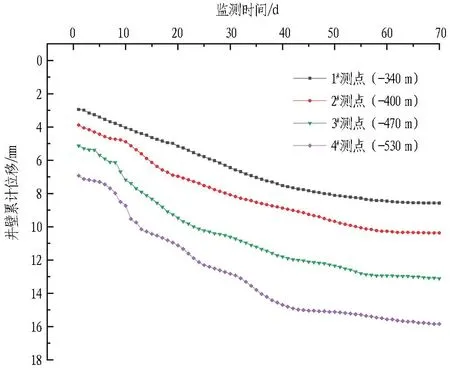
图9 井壁随深度变化的累计位移曲线

由图9可知,在竖井井筒深部注浆加固施工过程中,随着地层深度的增加,井壁位移逐渐增大,监测点均发生向竖井内侧移动,其中井壁底部(4#测点)处位移最大,但井壁累计位移最大不到16 mm,处于可控范围内,能够保证通风竖井的安全快速施工。

6 结论与讨论

本文对施工扰动和孔隙水压共同作用下隧道通风竖井的注浆帷幕安全厚度进行了系统研究,主要结论如下:

1)考虑竖井开挖过程中爆破扰动效应对已形成的地面预注浆帷幕体的影响,将注浆帷幕体的安全厚度划分为无效厚度和有效厚度2部分。通过建立注浆帷幕体力学分析模型,基于弹塑性力学理论与厚壁圆筒相关理论,提出了竖井注浆帷幕体安全厚度的计算公式。

2)运用本文理论研究成果确定了天山胜利隧道4号竖井注帷幕的安全厚度为6.5 m。依据厚壁圆环验算了注浆帷幕体的强度及稳定性,地面预注浆帷幕体的强度及稳定性符合设计要求。现场测试结果表明,竖井注浆堵水取得了良好的效果,可为竖井安全快速施工提供可靠保障。

由于注浆帷幕厚度是竖井安全快速施工的关键影响因素,除去本文重点研究的开挖扰动和孔隙水压的影响外,注浆帷幕合理厚度还与围岩岩性、浆液类型、注浆工艺及现场施工水平等因素密切相关,对此可进一步研究完善。