基于强化学习的盾构抗扰纠偏控制研究

赵文佳,石小伟,赵 茜,杨 璐,张艳丽,张亦敏

(中铁工程装备集团(天津)有限公司,天津 300450)

0 引言

盾构是用于隧道掘进和地下空间开发的专用设备,广泛应用于地铁和公路隧道施工[1-2]。为了防止掘进路线发生偏差,掘进过程中需不断通过推进系统来调节盾构的姿态。盾构的纠偏控制是以隧道设计轴线为目标,结合盾构纠偏设定值和测量反馈值,通过调整盾构掘进各分区的输出值,使盾构轨迹朝设定方向变化[3]。在实际施工中,盾构纠偏控制目前仍以人工控制为主。根据盾构的实时状态和工作人员经验人为控制推进系统。然而,人工手动纠偏容易导致实际轨迹偏离设计轨迹,偏差过大可能会发生沉降、坍塌等事故,故研究盾构的纠偏控制意义重大。

在复杂地质影响下,盾构负载多变、干扰源多,极大地影响盾构的纠偏控制,且传统的控制方式无法对盾构进行自适应的改变。为了解决盾构纠偏问题,学者们进行了相关的理论研究。Hu等[4]采用了一种数据驱动的盾构偏差预测方法,便于盾构驾驶员识别。Wang等[5]提出了一种基于盾构挖掘过程中数据驱动的轴线偏差预测和修正方法。Lyu等[6]提出将自适应鲁棒控制方法应用于阀门和泵的连锁液压控制系统,该方法提高了控制的鲁棒性,且使其具备出色的跟踪性能。对于盾构的轨迹纠偏控制,目前的主流控制方法为PID控制和模糊控制。Xie等[7]采用PID控制对盾构液压推进系统进行纠偏控制。Wu等[8]将自适应整定的模糊PID控制应用于推力液压控制系统,结果表明所提方法有较小的稳态位移误差。刘肖楠等[9]采用粒子群算法优化PID控制器参数,实现盾构纠偏控制,但是当系统出现较大扰动时,PID控制会出现较大波动,从而影响控制精度。

以上研究在纠偏方面取得了一定的成果,但是在解决实时的补偿扰动来提高盾构控制精度方面存在不足。自抗扰控制不依赖于被控对象的数学模型,通过扩张状态观测器,能对系统不确定性和未知扰动进行估计[10-12]。针对优化算法,模糊控制需要离线设计出模糊规则,设计较为复杂,而粒子群优化算法则缺乏对未知扰动的适应能力,因而需要一个优化算法,不仅能避免繁琐的模糊规则设计,而且能自适应地应对未知扰动。近年来,强化学习算法受到更多学者的关注[13-14]。强化学习不依赖于数学模型,通过与环境交互使累计奖励达到最大,将其应用于控制参数优化可提高控制器的自适应能力。

基于上述分析,针对盾构纠偏控制研究,考虑盾体姿态的扰动因素较多,且扰动因子的占比具有不确定性,故无法将扰动因子进行具体数字化。本文将传统的PID控制模型优化为自抗扰控制模型,结合强化学习中的Q学习算法实现自抗扰控制器参数的自适应整定。利用对推进系统的控制实现对盾构设定轨迹的跟踪,从而实现盾构姿态纠偏控制。具体的算法以盾构液压缸为控制对象,采用线性自抗扰控制(linear active disturbance rejection controller,LADRC)方法来解决模型的耦合和非线性问题,采用强化学习中的Q学习算法优化控制器参数。该方法简化了人工参数整定过程,增加了控制器的自适应能力,在实际掘进中更容易通过液压缸推力实现姿态纠偏控制。

1 盾构模型

由于盾构驱动、出渣、推进等系统之间存在强耦合和非线性等问题,无法对盾构进行精确地系统建模,具体系统结构见图1。

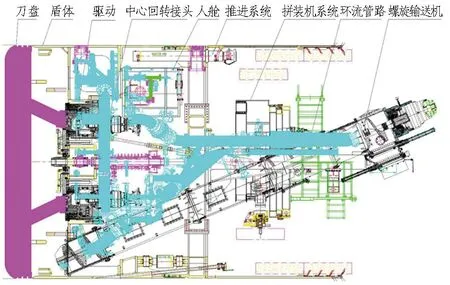
图1 盾构各系统结构图

常规盾构的推进系统主要有4个分区,推进系统分区示意见图2。

图2 推进系统分区

在掘进纠偏系统中实际使用为左、右分区,将左右分区的液压推进系统简化为数学模型[9]如下。

(1)

式中:F1和F2分别为左液压缸和右液压缸的反作用力;f为阻力;m为盾构的质量;y为盾构的轨迹;l1和l2分别为质心到接触点F1和F2的力臂;τ为阻力距;J为盾构旋转轴的转动惯量;θ为盾构的旋转角度。

考虑到实际施工要求,对y和θ进行近似化处理。

(2)

式中:l为2个推进液压缸之间的距离;y1和y2分别为左液压缸和右液压缸的轨迹。盾构液压缸的输出力与负载力平衡方程可表示为:

(3)

式中:i=1,2;A1i和A2i分别为液压缸无杆腔和有杆腔活塞面积;p1i和p2i分别为液压缸无杆腔和有杆腔压力;mi为活塞总质量;Bp为活塞的黏性阻尼系数;Kp为负载弹簧刚度;ωi为液压缸的输出力。

综上,可以得到盾构纠偏系统的动力学模型如下:

(4)

2 自抗扰控制器设计

自抗扰控制器的设计原理可参见文献[15]。针对盾构的纠偏控制,左液压缸和右液压缸的活塞杆位移的微分动态可以表示为:

(5)

(6)

(7)

(8)

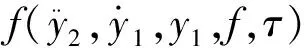
(9)

(10)

式(9)—(10)中h1和h2均为对应总扰动的微分。针对式(9)和式(10)设计对应的扩张状态观测器:

(11)

(12)

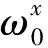
(13)

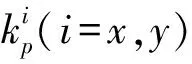
3 Q学习的控制参数整定

3.1 Q学习基本框架

Q学习[16]是强化学习的一个基础算法,Q学习基本框架如图3所示。在t时刻,智能体位于状态St,根据贪婪策略大概率选取Q表中Q值最高的动作at;通过和环境交互,智能体更新状态St+1并得到奖励值rt,进而更新Q表中的Q值;通过智能体和环境的不断交互,Q表得到充分更新;最后,智能体根据Q表实现当前状态下的最优控制。

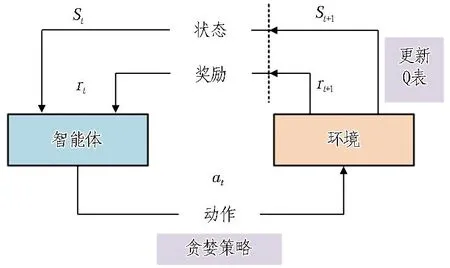
图3 Q学习基本框架

考虑到Q学习只能处理离散的数据,因此需要对控制过程中的部分变量进行离散化处理。

3.2 状态设计

将姿态角的跟踪误差与误差变化率定义为强化学习的状态。定义状态集如下:

(14)

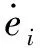
对误差和误差变化率进行离散化处理,分别将其划分为7个论域,其对应的语言变量为{NB,NM,NL,Z,PL,PM,PB}。则每个姿态通道有49个状态。状态划分如图4所示。

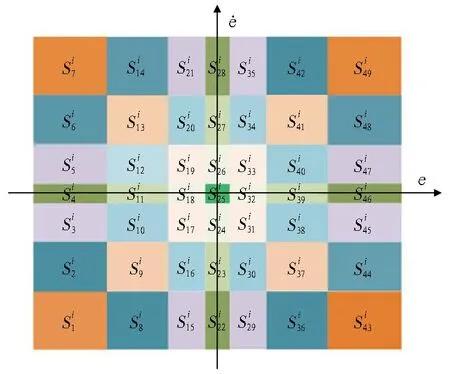
图4 状态划分

3.3 动作设计

将线性自抗扰控制的控制参数定义为强化学习的动作。定义动作集如下:

(15)

(16)

算法可以通过状态转移概率选取动作集中的动作值。状态转移概率选用的贪婪策略如下:

(17)

为了使动作集中的参数被充分训练,采用该策略可以在训练前期加大对非最优参数的探索能力。

3.4 奖励设计

为了使Q表训练得更加合理,性能函数被用来估计系统性能。设计性能函数:

(18)

根据性能函数,设计Q学习奖励模型:

(19)

3.5 Q表与训练设计

Q表中存储着每个状态下执行对应动作对系统影响的值,即Q值。通过状态模型的不断训练,Q表被不断更新。迭代的Q(St,at)值表达式如下:

(20)

式中α和γ分别为学习率和折扣因子。

概述Q学习优化的训练过程为:

1)Q学习根据当前控制偏差,按照贪婪策略从Q表中选取控制参数,并将其作用于设计模型,盾构会根据左右液压机状态反馈这一时刻的控制误差。

2)模型根据反馈的控制误差对算法进行奖励或者惩罚,进而更新Q值,并对控制器参数进行再次优化。

3)通过不断迭代训练,Q表中会存储着当前控制误差下应采取的最优控制器参数。当训练完毕时,可以将训练后的Q表用于盾构的纠偏控制过程。

3.6 偏差整定

在训练过程中,为了防止系统状态发散,当误差或误差导数超过一定阈值时(即图4区域以外的值),本次训练会提前终止。

本次设计的盾构纠偏控制框架如图5所示。采用2个独立的Q学习模型来分别整定2个线性自抗扰控制器参数。在控制过程中,当盾构的轨迹发生偏移时,模型会根据偏差,控制液压缸的推力,对控制轨迹进行纠偏,从而达到盾构姿态控制的效果。Q学习作为强化学习的算法,会根据当前的偏差从训练后的Q表中选择合适的控制参数,实现对控制器参数的自适应整定。

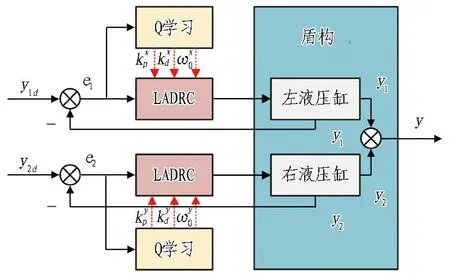
图5 基于Q学习的盾构纠偏控制

4 仿真测试及模型对比

对盾构纠偏模型进行仿真测试,通过Q学习算法分别对2个控制器参数进行整定。为更好地验证所提方法的有效性,对比传统PID和线性自抗扰控制,仿真结果验证了所提控制方法的有效性。

4.1 参数设置

在仿真模型中对盾构纠偏模型参数进行设置,具体参数如表1所示。

表1 盾构纠偏模型参数

表2 状态论域划分

4.2 模型曲线对比

盾构的左、右液压缸轨迹跟踪分别如图6和图7所示。由图可以看出:由于存在较大的阻力和阻力矩,传统的PID控制响应速度很慢,左右液压缸的跟踪轨迹约在10 s后进入稳态,且存在较大的稳态跟踪误差。对于Q学习盾构纠偏模型,由于扩张状态观测器的存在,其能更好地处理盾构运行过程中的扰动。

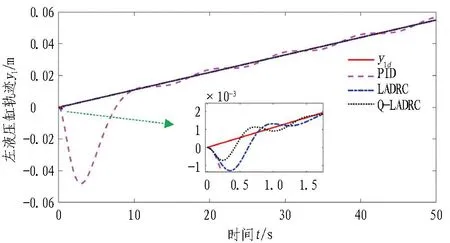
图6 左液压缸轨迹跟踪曲线

图7 右液压缸轨迹跟踪曲线

仿真整体盾构主机段的近似轨迹如图8所示。由图可以看出:左右液压缸的跟踪轨迹约在1.5 s后进入稳态。与LADRC相比,本文所提的控制方法Q-LADRC能够减少轨迹跟踪的超调量,误差跟踪变化幅度更小,证明了模型的有效性。

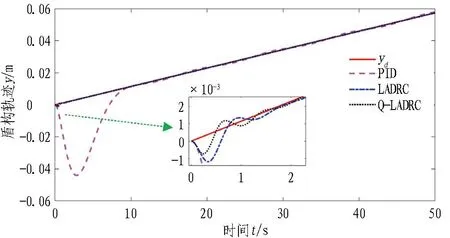
图8 盾构轨迹跟踪曲线

4.3 性能指标判定

对不同模型的轨迹跟踪的误差跟踪性能指标进行统计,得到数据如表3和表4所示。分析得到,本文所提方法Q-LADRC各个误差指标均为最小,说明其能更好地控制精度和响应速度。

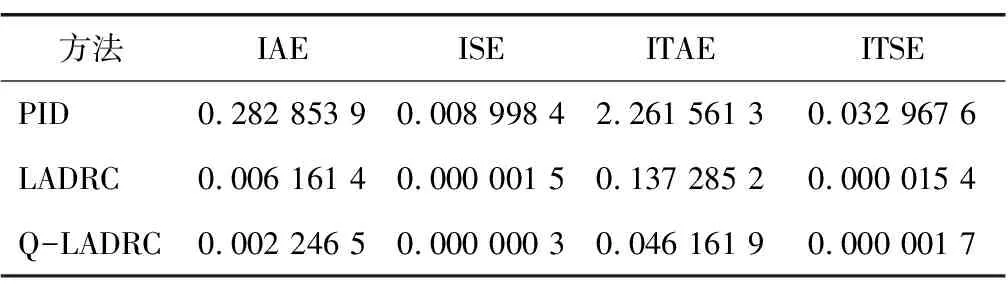
表3 y1误差性能指标

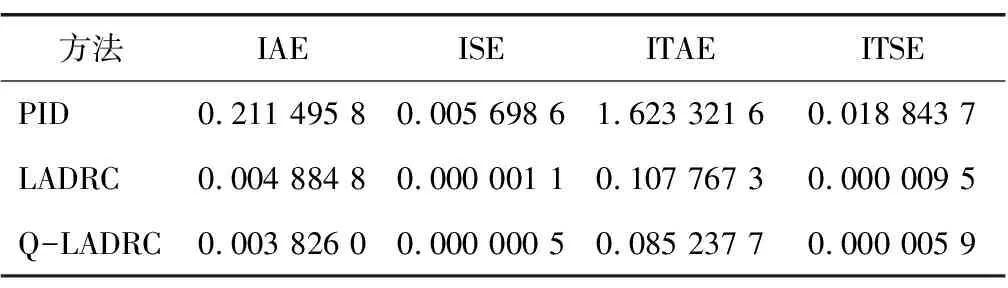
表4 y2误差性能指标

分析不同模型轨迹跟踪过程中的左、右液压缸控制参数变化情况,分别如图9和图10所示。由图可以看出:Q学习会根据控制过程中的误差,自适应地调整控制器参数。该方法能够较好地减少繁琐的人工调参频次,同时增强传统控制的自适应能力。

图9 左液压缸控制参数变化

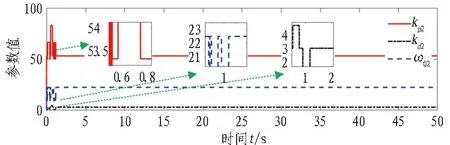
图10 右液压缸控制参数变化

5 结论与讨论

利用仿真模型的验证和对比,得到结论如下:

1)相比传统的PID控制,本文提到的方法响应速度较快,左右液压缸的跟踪轨迹稳态跟踪误差值也较小,体现出较高的控制精度,证明该模型在盾构纠偏姿态跟踪中的有效性。

2)相比于LADRC相比,本文所提的控制方法能够减少轨迹跟踪的超调量,误差跟踪变化幅度更小,有效减少了人工参数整定过程,同时提高了控制的精度和收敛速度,说明该模型在非耦合性和不确定性干扰源的情况下,对盾构姿态具备更好的纠偏效果。

本方法在理论上证明了对盾构纠偏功能的有效性,后期可在实际应用中展开深入研究,搭建独立运行的算法软件包,与设备PLC及导向系统进行数据交互运算,处理推进系统实时数据并输出决策参数,应用于自动轴线纠偏系统的液压控制系统,实现理论到实践的转化。