基于高光谱的山区耕地土壤有机质含量估测

张永亮, 汪 泓, 肖玖军, 李可相, 王 宇, 邢 丹

(1.贵州大学矿业学院,贵州 贵阳 550025; 2.贵州省山地资源研究所,贵州 贵阳 550001; 3.贵州省土地绿色整治工程研究中心,贵州 贵阳 550001; 4.贵州省农业科学院辣椒研究所,贵州 贵阳 550009)

贵州全省山地面积占比近90%,是全国唯一一个没有平原支撑的省份[1]。山区耕地的零碎化分布,导致部分耕地利用率低,土壤质地分布不均,在一定程度上限制了农业生产。土壤有机质(Soil organic matter, SOM)是存在于土壤中的含碳有机化合物的总和,具有提供养分、保水保肥、促进土壤团粒结构形成及改善土壤理化性质等作用[2-3],其含量是衡量土壤肥力的重要指标,快速、准确地监测SOM含量对于山区耕地科学管理具有重要意义。传统的SOM含量测定主要通过田间取样、实验室化验分析,该方法使用成本较高且效果欠佳[4]。近年来,高光谱遥感技术以其时效高、信息量大且无污染的优势逐渐在SOM快速检测中得到应用[5]。

近年来,研究者针对不同地区的土壤性质,利用高光谱遥感技术从数据处理和模型算法等方面反演出契合当地的SOM预测模型。韩兆迎等[6]通过相关分析确定了7个特征波段,建立了SOM含量估测模型,发现用二次多项式逐步回归模型反演黄河三角洲土壤SOM含量的效果最优;勾宇轩等[7]用小波变换结合稳定性竞争自适应重加权采样(Stability competitive adaptive reweighted sampling, CARS)算法,较好地反演了东北旱作农田土壤类型的SOM含量;南锋等[8]使用偏最小二乘回归(Partial least squares regression, PLSR)分析方法,建立了能够很好地反演黄土高原煤矿区复垦农田SOM含量的模型。Nawar等[9-10]利用便携式光谱仪(Analytical Spectral Devices FieldSpec4 Standard-Res,ASD)获取埃及四奈北部地区土壤光谱信息,对光谱数据采用7种预处理技术预处理之后构建线性PLSR、非线性支持向量机回归(Support vector machine,SVM)和多元自适应回归样条(Multivariate adaptive regression splines,MARS)等3种模型进行盐渍土有机质含量的预测,交叉验证结果显示,MARS模型的预测效果最佳。张娟娟等[11]将遗传算法与SVM回归结合进行砂姜黑土SOM含量的估测,发现决定系数(R2)高达0.95。张森等[12]用反向传播(Back propagation,BP)神经网络、SVM模型对滨海湿地土壤有机质含量进行估算,结果显示,用SVM模型估测的SOM含量在精度方面明显更优。钟亮等[13]基于卷积神经网络(Convolutional neural network, CNN)模型,探讨不同网络结构对SOM含量预测的建模效果,经大量训练得出,小卷积核的VGGNet-7适用于红壤地区SOM含量的预测且CNN能够简化光谱预处理过程。

从以上研究结果可以看出,估测SOM含量的机器学习方法大多基于线性与非线性模型,各地区适用的模型均不相同,主要与土壤的光谱特性、数据处理和建模方法的选择有关。从目前的研究内容看,基于平原地区展开的研究相对偏多,这是由于其成土母质受到适宜的湿度、光照条件的影响,使得土壤理化性质良好,因此通过线性模型即可稳定高效地对该地区SOM含量进行反演,如武彦清等[14]分别采用多元线性逐步回归和PLSR 2种方法建立的模型均能满足松嫩平原SOM含量的速测要求,陆龙妹等[15]利用PLSR方法建立的SOM含量光谱预测模型能预测出淮北平原SOM含量,文锡梅等[16]利用PLSR模型定量反演出喀斯特地区SOM含量并获得较好的模型精度,但小范围研究区和单一种类土壤建模的模型通用性还较为欠缺。贵州省内地喀斯特地貌分布广泛,地形复杂且气候多变,土壤干旱、侵蚀现象较为严重,耕地分布零碎且土壤类型多样,在此地进行大范围土壤光谱监测容易造成光谱数据冗余,反演出的模型在进行较大尺度SOM含量估算时精度欠佳。因此,运用合适的模型算法估测山区耕地SOM含量是当前亟待解决的问题之一。本研究拟以从贵州山区耕地采集的120个土壤样本为研究对象,通过ASD便携式地物光谱仪采集样品光谱,在PLSR基础上探讨非线性模型[SVM、随机森林(Random forest, RF)、BP]在山区耕地SOM含量反演中的结果,通过对比分析以获得精度最高的光谱变换和模型组合,以期为山区耕地SOM含量估测提供快速可靠的算法。

1 材料与方法

1.1 研究区概况

贵州省地处中国西南内陆腹地,在地形上属于中国西南高原山区,地势特点是自西向东低,由中向北、向东、向南倾斜。研究区选取贵州省贵阳市、遵义市、黔南州、黔东南州和毕节市等5个地区下辖的13个县(区、市),图1是研究区内部分采样点及其13个县(区、市)的边界范围,采样点耕地分布在山地、丘陵和沟谷等地域,在海拔620～1 580 m内采集土样,土类以黄壤、黄色石灰土、水稻土和紫泥土为主。贵州省占比最高的土壤类型是黄壤,占全省土壤面积的46.4%[17];黄色石灰土分布范围最广,各地均有分布,但相对集中分布在黔中地区,大泥土属于黄色石灰土的一类;水稻土是贵州省农业生产中极为重要的土壤资源,92.8%水稻土分布在海拔1 400 m以下的区域;紫泥土的面积相对较少,主要分布在黔北、黔西北等高海拔地区。据前人记载,贵州省山区的SOM含量总体较高,但由于耕地分布零碎,导致其撂荒严重[18]。

图1 研究区域的部分采样点分布

1.2 土壤样品采集与处理

根据贵州省土壤空间分布特征,于2020年8月至2021年3月在研究区开展土壤取样,共计120个土壤样品,研究区域土壤概况见表1。在研究区内采集耕地表层20 cm以内的土壤作为样本,用手持全球定位系统(GPS)定位并随时记录相关信息。经实验室风干、去杂、研磨后过2 mm筛,分成2份,分别用于光谱采集和有机质含量的测定。土壤有机质含量的测定采用重铬酸钾-硫酸硝化法[19]。

1.3 土壤高光谱数据的测定

土壤原始光谱反射率的采集使用ASD便携式地物波谱仪,光谱范围为350～2 500 nm,光谱重采样间隔为1 nm,在暗室条件下测定,将土样放入直径15 cm、深度2 cm的硼硅玻璃皿中,用尺子刮平表面。将高密度探头贴近土壤样品,使探头视野充满土壤样品,固定探头后垂直对准被测物体。光源使用高密度探头自带光源,成功进行初始白板校正后,确保高密度探头和土壤样品的相对位置保持不变。在获得原始光谱反射率后,再将土壤样品旋转3次,旋转角度为90°,分别采集10条光谱曲线,土壤样品的光谱反射数据为10条光谱曲线的均值[20]。每间隔15～20 min重新进行优化。

1.4 数据预处理

由于土壤样品光谱曲线边缘的350～400 nm、2 400～2 500 nm部分受到外界噪声的影响较大,因此将其去除以减少干扰。在OriginPro 2021软件中用Savitzky-Golay(SG)[21-22]滤波进行9点平滑去噪处理,该滤波方法是一种在时域内基于局域多项式最小二乘法拟合的滤波方法,其最大特点是在滤除噪声的同时可以保持信号的形状和宽度不变。为更有效筛选山区土壤光谱的特征波段,对平滑后的原始光谱反射率(R)进行一阶微分(First derivative,FD)、二阶微分(Second derivative, SD)、倒数对数的一阶微分(First derivative of reciprocal logarithm,LRD)、连续统去除(Continuum removal,CR)等4种变换处理。光谱一阶微分处理可在消除背景噪声干扰的同时提高光谱分辨率、降低相关波段的寻找难度[23-25],倒数对数变换法可减少乘数因子对光照条件变化的影响[26],连续统去除法有利于突出光谱曲线的吸收、反射特征,分类识别提取敏感波段[27-28]。上述过程中的FD、SD、LRD处理在Matlab R 2016b、The Unscrambler X10.4软件中完成,CR处理在ENVI 5.3中完成。

1.5 模型的构建与精度验证

PLSR集结了主成分分析、典型相关分析和线性回归分析的特点,在同时包含多个变量的情况下能实现多对多的模型构建,并在一定程度上解决自变量之间共线的问题[29],因此采用The Unscrambler X10.4软件的PLSR模块完成SOM含量反演模型。

SVM可将数据从低维空间映射到高维空间中,然后在此高维空间中进行线性回归,从而取得在原空间非线性回归的效果[30-31]。SVM模型构建在Matlab中完成,SVM模型参数设定如下:类型选择C-SVC,核函数类型为RBF,惩罚因子(Cost)为1,核函数系数(Gamma)为0.001,损失函数的P值为0.01,收敛精度(Eps)为0.001[32]。

RF属于机器模型,它通过随机方式形成了由多个决策树组成的一片森林,当新样本作为数据变量输入到构建好的森林中时,森林中的每棵决策树就会分别判断并识别这个样本所属的类别[33],再统计哪个类别被判定得最多,进而预测该样本所属的类别。RF可产生高准确度的分类器,处理大量的数据变量,在判断类别时还能考虑变量的重要性,且训练速度快。RF模型构建在Matlab中完成,RF的参数设置如下:决策数目(Ntree)为200,训练节点变量数(Mtry)为2。

表1 研究区域的土壤概况

BP神经网络是一种非线性映射模型,具有完整的数学算法,理论上能够无限逼近任意复杂的非线性函数[34],对于样品较多的机器学习问题,传统的线性回归会存在欠拟合或过拟合现象,神经网络可以让它们不断训练以达到最好效果。BP神经网络模型在Matlab中完成,训练参数设置如下:迭代次数为1 000次,训练均方根误差小于10-5,神经元设置为5个,学习率为0.05,最大失败次数为5次,经过试凑法最终确定BP神经网络模型隐含层节点数依次为3个、6个、9个[35]。

模型精度测试用如下3个参数进行评估:决定系数(Determination coefficient,R2)、均方根误差(Root mean square error,RMSE)和相对分析误差(Residual predictive deviation,RPD)。其中,R2用于测量模型的稳定性,R2>0.6表明模型能够粗略预测SOM含量;R2>0.8,表明模型的稳定性较强[36]。RMSE用来检验模型的预测能力,RMSE越小,表明模型的精度越高。RPD用来评价测试模型的预测能力,当RPD>2.0时,说明模型的预测效果较好;当1.4≤RPD≤2.0时,说明模型具有基本预测能力,经过改进后预测效果更好;当RPD<1.4时,模型预测能力较弱。相关公式如下:

(1)

(2)

(3)

(4)

2 结果与分析

2.1 土壤有机质含量的统计分析

将120个土壤样本按有机质含量从大到小排序,根据有机质含量梯度,按照3∶1的比例选取训练样本和测试样本,最终确定90个训练样本、30个测试样本。由表2可以看出,土壤有机质含量为11.40～48.60 g/kg,均值为28.91 g/kg,标准差为8.31 g/kg,训练样本、测试样本的标准差分别为8.24 g/kg、8.53 g/kg,总体变异系数偏中等。

表2 贵州山区土壤有机质含量的统计分析结果

2.2 土壤有机质含量的光谱相关分析

山区耕地的土壤高光谱在5种不同形式下与SOM含量之间的相关性分析结果见图2。可以看出,原始光谱(R)与SOM含量整体呈负相关并在可见光部分相关系数达到极值(图2a);4种光谱变换处理下,在可见光-近红外光范围内均有波段在正负值之间波动,并且有不少波段通过0.01水平的显著性检验;经FD变换提高了光谱与SOM含量在近红外范围内的相关性,敏感波段从可见光至近红外光之间呈均匀分配,有1 494个波段通过显著性检验,且与SOM含量呈极显著相关(P≤0.01),相关系数最高为-0.635(图2b);SD处理后的光谱在近红外部分频繁出现吸收谷、反射峰,敏感波段范围也集中在此部分,统计有461个波段与SOM含量呈极显著相关(P≤0.01),相关系数极值为-0.561(图2c);LRD与FD数据的变换相似,共有1 455个敏感波段,由于先经过倒数对数变换的原因,LRD与FD的相关系数图类似于对称分布,相关系数极值为0.512(图2d);通过CR变换,使得土壤光谱和有机质含量间大部分呈正相关,说明CR变换能增强山区土壤光谱的吸收特征,通过显著性检验的波段有1 035个,相关系数极值为0.514(图2e)。基于相关系数绝对值、通过显著性波段数量,得出如下排序:FD>LRD>CR>SD,该排序说明,光谱数据经过FD、LRD变换后能提高山区耕地SOM含量与光谱波段之间的相关性,更有利于筛选特征波段。

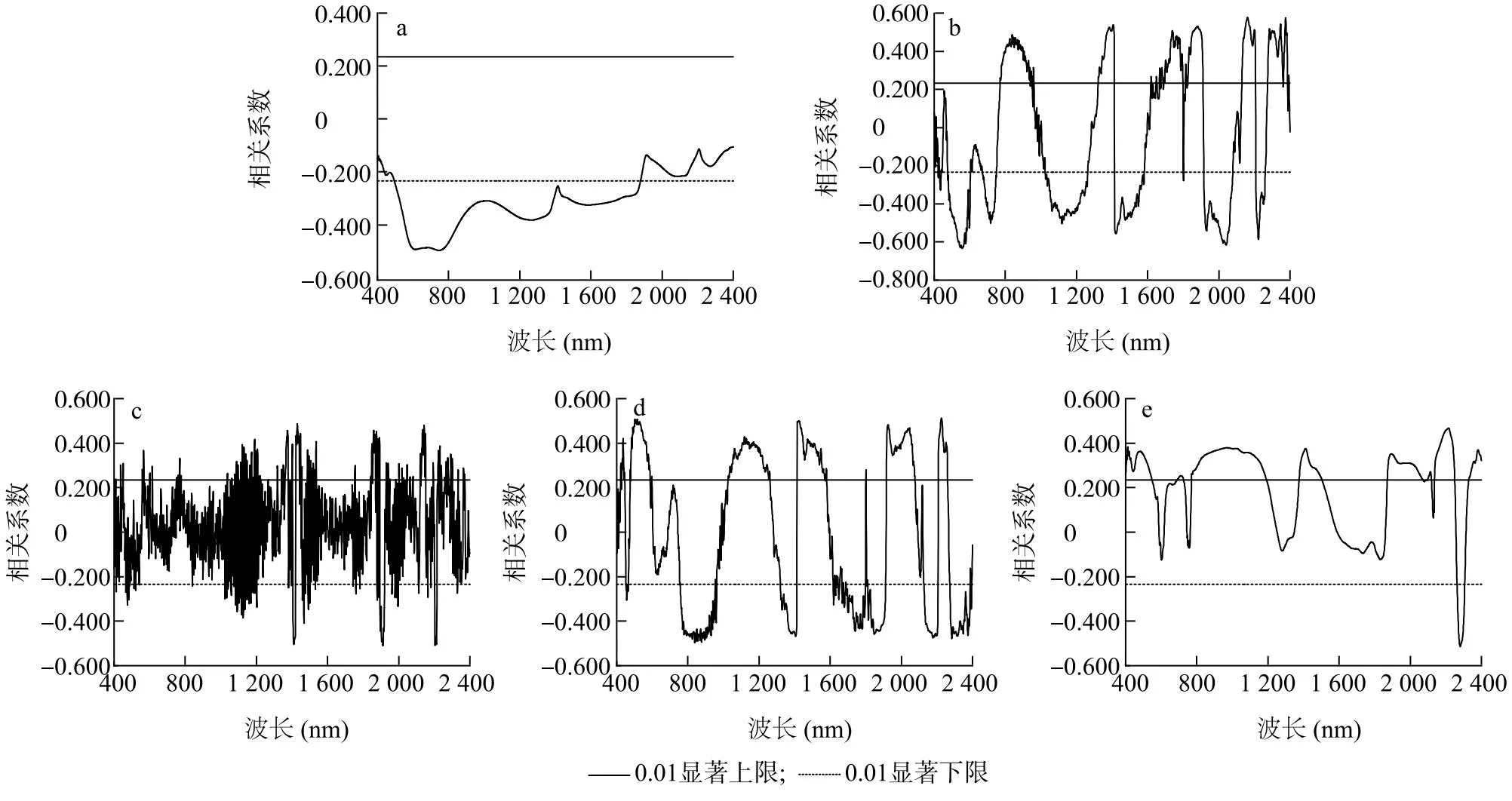
a:原始光谱;b:一阶微分;c:二阶微分;d:倒数对数的一阶微分;e:连续统去除。

图3为SOM含量与不同形式光谱间相关性分析的特征波段范围,可以看出,原始光谱的特征波段大多集中在可见光部分,经光谱技术变换后,在不同程度上挖掘出近红外部分的特征光谱信息,说明可见光-近红外光范围都蕴含山区耕地土壤的特征波段,所以本研究通过显著性检验后,在不同变换形式的光谱中筛选出它们在可见光-近红外光部分相关系数较高的60个波段用于建模。这与于雷等[37]利用竞争性自适应重加权-连续投影算法筛选得到的建模波段以近红外光(1 800～2 400 nm)部分为主的结果有差异。推测其原因,可能由于研究区及土壤类型不同,前人以江汉平原的潮土、水稻田和黄棕壤为研究对象,该地区雨量充沛且土壤耕作程度高,其土壤含水量相对较高,而土壤含水量的光谱特性主要集中在近红外波段范围[38],因此土壤含水量会影响土壤反射率和有机质含量相关的光谱信息。由于在1 400 nm、1 900 nm和2 200 nm等波段附近具有强烈的水分吸收谷,与黏土矿物中所含的OH-有关[39],因此最后获得的5种光谱的特征响应波段应将其剔除。

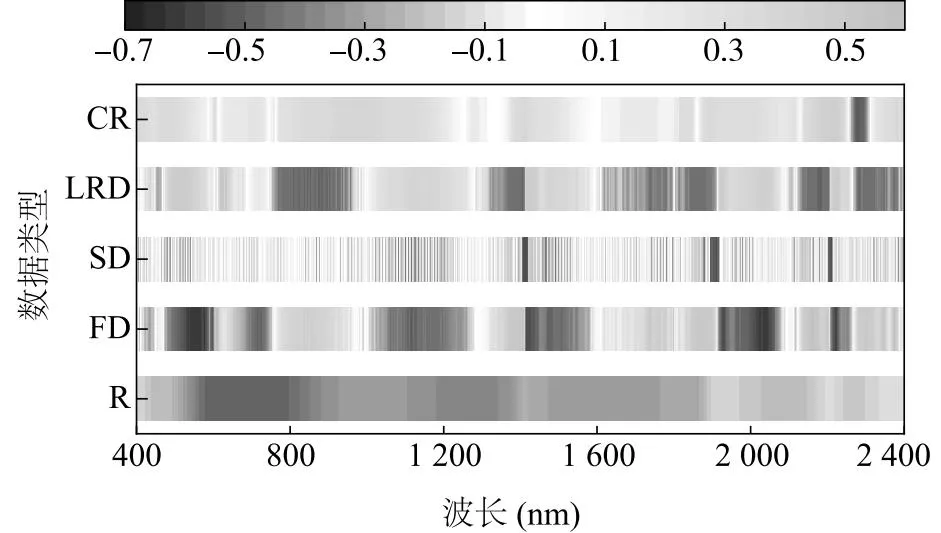
CR:连续统去除;LRD:倒数对数的一阶微分;SD:二阶微分;FD:一阶微分;R:原始光谱反射率。

2.3 不同估测模型SOM含量反演的结果

表3是山区耕地SOM含量反演的不同光谱变化和模型组合,可以看出,训练集的模型预测精度基本高于测试集,可能与二者样本数量差异有密切关系。基于偏最小二乘回归的模型中,除了SD光谱变换反演的模型外,其余3种光谱变换的模型均能达到预测土壤有机质含量的基本要求,表现最好的是LRD,测试集的R2、RPD分别为0.717(>0.600)、1.894(>1.400),而SD的精度最低(其测试集的R2、RPD分别为0.457(<0.600)、1.357(<1.400),不适用于山区耕地SOM含量的反演。SVM模型相对PLSR反演SOM含量的效果整体呈现略微下降的趋势,虽然总体R2均大于0.600,但模型拟合效果一般,不能作为山区耕地SOM含量估测的首选模型。在反演SOM含量的效果上,RF模型相较于PLSR有明显提高,其中训练集的R2均远高于同等变换的其他模型,R2最高达到0.926,因此在训练集中,RF可作为理想的估测模型使用,测试集中FD、SD、CR的R2均大于0.750,RPD均大于2.000,整体模型预测效果表现良好。4类模型中,BP神经网络预测模型的预测能力最高,测试集经过FD、LRD数据变换组合的BP神经网络模型R2均在0.800以上,与它们对等的训练集间的差距进一步缩小,与RF相比具有明显优势,BP建模效果最佳的模型组合是FD-BP,训练集的R2为0.845,RMSE最小,为3.259,测试集的R2为0.838,RMSE为3.452,RPD为2.470,相对分析误差以FD最高,说明BP神经网络模型在预测山区耕地SOM含量方面具有较高的稳定性,可以进行有效预测。图4为30个测试样本代入训练模型所得到实测值与预测值的散点图,通过分析20个模型各项精度指标,能够筛选出反演效果最好的6个模型组合。

表3 不同组合形式土壤有机质含量的光谱反演模型精度

通过综合训练集和测试集各项验证指标分析发现,在不同变换的光谱数据与模型组合中,FD-BP模型具有最稳定的估测能力,其次是LRD-BP、R-BP、FD-RF、SD-RF和CR-RF模型,有良好的预估能力。在数据变换方面,能提高模型预测SOM含量精度的光谱变换排序是FD>LRD>CR>SD。在模型选择方面,更适合山区SOM含量反演的模型依次为BP、RF、PLSR、SVM。

3 讨 论

由建模结果可以看出,经过FD、LRD的光谱数据变换组合的模型反演效果较好,表明FD、LRD变换不仅能消除光谱曲线周围噪声、提高光谱分辨率,还能突出可见光至近红外范围波段间的差异,提高光谱与SOM含量之间的相关性,增加敏感波段的数量,使建模精度得到保障,这与前人的研究结论相符[40];而SD变换让光谱与SOM含量相关性分析反应过甚,敏感波段间多重相关,无法有效提取山区土壤信息,导致建模效果不理想;CR与原始光谱组合的模型效果对比没有明显变化,推测是因为相关系数偏低且敏感波段数量偏少,因此建模效果一般。

针对贵州省山区耕地分布零碎、土壤类型多样等问题,本研究的采样区域零星遍布于贵州省13个县(区、市),涵盖黄壤、黄色石灰土、水稻田和紫泥土等土壤。由于土样种类多且研究区域广,光谱在有效范围内蕴藏的土壤信息易出现重合、交叉等问题。与以往学者的研究结果相比,在筛选特征波段方面,本研究根据相关系数由大到小的原则,有间隔地挑选出敏感波段及波段范围,并且在原始及其他变换的光谱中选取同样数量的特征波段用于建模,既能降低高光谱数据冗余,又可保证后期山区耕地SOM含量反演模型的客观性。

本研究对线性模型(PLSR)和非线性模型(SVM、RF、BP)进行试验对比,探讨不同模型对贵州山区耕地SOM含量反演的实用性。研究得出,非线性建模效果更佳,这与周伟等[41]通过PLSR、SVM、RF对三江源地区土壤有机质含量反演得出的结论一致。经典线性模型PLSR反演出的模型效果仅能达到山区耕地SOM含量估测的基础水平,原因可能是PLSR没有充分提取出山区SOM含量的主成分信息,在未来的试验中,可事先采用主成分确定各类SOM含量相关性最大的波段范围,通过综合对比筛选出有效光谱波段进行建模以提高PLSR的精度模型。本研究与前人研究的不同之处在于,SVM模型精度没有达到理想效果,推测与SVM所选用的RBF核函数有关,本研究中测试集的特征波段数量远大于样本数量,当核函数映射维度非常高时,计算量过大,导致SVM泛化能力变差,而可见光、近红外光2个部分含有大量山区SOM含量不可或缺的特征波段。可选择Polynomial或Sigmoid核函数再利用交叉验证方法寻找最佳参数以优化SVM的反演效果[42]。RF测试集与训练集的精度相距甚远,离散程度大,造成测试集存在欠拟合的现象,可能与样本数量有很大关系,同时说明随机森林更适合对多变量的数据样本进行建模。综合4类模型比较发现,BP神经网络模型可以更精准地反演山区SOM含量,这与BP神经网络可以实现以任意精度逼近任何连续函数有关[43],即它能随研究对象复杂程度的增加,通过调节隐含层节点数以提高模型精度。

BP、RF、R、FD、SD、LRD、CR、R2见表3注。

另外,本研究重在讨论适用于贵州山区耕地SOM含量的估测模型,但受到贵州山区地形条件限制,部分研究区位于山高坡陡区域,耕作化程度低且交通不便,导致采样难度大、样本数量偏少。后续研究中我们将扩大采样范围和样本数量,优化分析以进一步提升模型的通用性。

4 结 论

贵州山区土壤的高光谱数据通过SG光谱预处理和4种光谱数据变换,在不同程度上提高了它们与SOM含量之间的相关性,其中一阶微分变换可充分挖掘山区土壤信息,通过显著性检验的波段数多达1 494个,相关系数最高达到-0.635。

与SOM含量进行相关性分析得出的敏感波段数量越多且范围(可见光-近红外)越宽,其构建的模型效果越好,说明通过相关系数由大到小的原则在光谱有效范围内均匀筛选的波段不仅能代表土样信息,还能在建模时减少自变量之间多重相关等问题。在估测山区耕地SOM含量方面,PLSR具有粗略的估测能力;SVM模型对山区耕地SOM含量的建模效果不佳;RF优于前两者但测试模型精度一般;非线性模型中BP神经网络以其精度高、稳定性好等特点而适用于山区耕地SOM含量估测,以一阶微分-BP神经网络预测效果最优(训练集:R2=0.845,RMSE=3.259;测试集:R2=0.838,RMSE=3.452,RPD=2.470),对于贵州多地区SOM含量的监测更具备普适性。