基于长短期记忆网络的移动轨迹目的地预测*
晋广印,赵旭俊,龚艺璇
(太原科技大学计算机科学与技术学院,山西 太原 030024)
1 引言
随着嵌入式GPS设备(如手机和智能手表)的普及,基于位置服务和应用LBSA(Location-Based Services and Applications)极大改善了人们的生活体验,同时这些设备也记录了海量的轨迹数据,促进了LBSA领域的发展。近几年,LBSA迈入了一个新的阶段,在推荐系统、智能交通系统和智能导航系统等方面起到了不可替代的重要作用[1-3],而这些服务和应用都需要对轨迹的目的地以及未来的路径进行预测,如何快速准确地预测移动轨迹的目的地逐渐成为众多学者关注和研究的热点问题。
现有的轨迹目的地预测方法是将真实轨迹数据抽象为易于处理的抽象表达方式[4],在此基础上构建合适的预测模型,以实现预测。目的地预测任务的实现需要海量的历史轨迹作为数据支撑,现实中收集到的轨迹往往不能包含所有可能的查询轨迹(数据稀疏问题)[5],即由于道路的复杂性导致当前查询轨迹并不存在于历史轨迹库中,或者是当前查询的前缀轨迹与历史轨迹库中的一部分轨迹相似度很高,但目的地却不相同。现有解决稀疏问题的方法主要包含2类:一类是将轨迹映射到二维平面上,通过调节粒度的方式缓解数据稀疏问题,但是粒度的调节受数据集影响较大,在面对新数据集时实施困难。另一类是将轨迹进行网格划分,但没有考虑轨迹网格之间的地理拓扑关系,而不考虑空间因素势必会降低预测结果的准确性。因此,数据稀疏问题如果不能得到有效的解决,会严重影响预测准确性。此外,轨迹数据特征更偏向于序列数据,前缀轨迹点对预测结果的影响是不同的(长期依赖问题),现有的研究工作只关注了前缀轨迹整体对预测结果的影响,而忽略了一些关键点。
针对以上问题,本文提出了基于长短期记忆LSTM(Long Short-Term Memory)网络的移动轨迹目的地预测方法。在轨迹表征方面,提出了轨迹分布式表示方法,通过geohash算法对分段后的轨迹进行网格划分,之后通过Base2vec模型对划分后的网格进行训练,将由二进制表示的网格转化为具有地理拓扑关系的向量表示。然后对目的地进行聚类,为轨迹添加伪标签,缩小相似轨迹的差异,放大不相似轨迹的特征,将序列预测问题转化为序列分类,以克服数据稀疏问题带来的负面影响。同时提出了基于LSTM网络的移动轨迹目的地预测模型SATN-LSTM(Self-ATteNtion-LSTM),对LSTM网络结构进行优化,将自注意力机制引入LSTM网络中,挖掘序列中的关键点并根据其重要程度分配权重,较好地解决了长期依赖问题。
2 相关工作
2.1 数据稀疏问题
数据稀疏问题是目的地预测任务中容易被忽略且较为常见的问题,由于现实中收集到的轨迹远不能包含所有可能的查询轨迹,会影响最终的预测精度。造成数据稀疏问题的原因可分为以下2点:(1)现实中收集到的轨迹数据集有限;(2)由于嵌入式GPS设备采样频率不同,导致相同的轨迹存在较大的差异。为了解决数据稀疏问题,江婧等人[6]提出了一种基于卷积神经网络CNN(Convolutio- nal Neural Network)的轨迹目的地预测方法。该方法首先对轨迹进行分段,然后将轨迹序列表示为二维黑白图像,并为图像添加标签,采用卷积神经网络提取轨迹图像特征,将目的地预测问题转化为图像分类问题。随后Lü等人[7]在此基础上对原始轨迹序列进行多粒度分析,并将整个前缀轨迹转化为图像,验证了轨迹起始位置对预测结果具有非常重要的作用。Wang等人[8]通过负抽样策略对原始数据进行低维表示,利用带有注意力机制的卷积神经网络在不同的数据集上也得到了类似的结论。此外,Song等人[9]提出的基于循环神经网络的方法,在将轨迹进行网格划分并转化为向量表示来解决数据稀疏问题时,没有考虑轨迹点之间的地理拓扑关系。多数目的地预测方法在解决轨迹数据稀疏问题上具有明显的局限性,对此本文对原始轨迹进行了分段处理,并将分段后的轨迹转化为轨迹网格表示,采用分布式表示方法,赋予轨迹网格地理拓扑关系,缩小相似轨迹的差异,放大不相似轨迹的特征,以克服数据稀疏问题带来的负面影响。
2.2 长期依赖问题
长期依赖问题是指目的地预测的准确性不仅仅依赖较近时间的前缀节点,而且对较远时间的前缀节点具有长期依赖关系,时间较早的前缀轨迹点往往被忽略,这与实际情况不符,且会降低预测的准确性。Zhang等人[10]提出了一种名为数据驱动的集成学习方法来预测目的地,首先确定最可能的未来位置,并通过马尔科夫转移矩阵得到2个位置之间的转移概率,然后通过贝叶斯推理,结合转移概率来预测目的地,但概率统计学模型具有严重的长期依赖问题。Yang等人[11]通过数据嵌入的方法对数据进行降维处理,在特征选择之前将数据嵌入二维空间,并使用数据驱动的集成学习方法进行移动轨迹的目的地预测,获得了较好的预测性能。近几年,以神经网络为基础的深度学习技术引起了众多研究人员和学者的关注,并在轨迹目的地预测任务中得到了广泛的应用。Xu等人[12]在LSTM网络结构中引入了时间门和距离门结构,以捕获连续位置之间的时空关系,但是不相邻位置之间的关系并没有考虑。Gui等人[13]提出的一种基于位置语义的注意力感知长短期记忆网络模型,在LSTM中引入了注意力感知模块。Rossi等人[14]从司机的角度出发,为司机的行为进行建模,同样采用了LSTM网络并加入了注意力机制以缓解轨迹序列的长期依赖性问题,但是传统的注意力机制参数量大,调整困难。此外,有一种兴趣点预测方法与轨迹目的地预测方法类似,兴趣点预测是对用户的历史兴趣点签到记录进行信息挖掘,来预测下一个时间片用户最有可能访问的位置。Qian等人[15]提出了一种新的基于协作注意力的兴趣点预测网络,该网络使用了内外轨迹相关性,获得了较好的预测效果。Huang等人[16]开发了基于自注意力的时空LSTM网络,使用时空上下文信息选择性地关注嵌入序列中的相关历史嵌入记录,得到了更好的表现。兴趣点预测与轨迹目的地预测相比,预测模式相同,即通过对历史信息的学习来预测未来一段时间内移动对象的目的地。不同之处在于兴趣点预测以时间片为单位,关注的是下一个时间片最有可能访问的位置,也可称作下一个兴趣点推荐。轨迹目的地预测是根据现有未完成的轨迹(前缀轨迹)来预测此次出行的目的地。并且兴趣点预测多用于人的轨迹,而轨迹目的地预测多用于网约车的轨迹。本文将自注意力机制引入LSTM网络中,挖掘轨迹序列中的关键点并根据其重要程度分配权重,以解决了长期依赖问题。
3 轨迹数据处理
3.1 相关定义及轨迹数据处理流程
定义1(第k条轨迹Tk的序列表示)Tk={Pk1,Pk2,…,Pkn-1,Pkn},轨迹序列Tk由一系列按时间顺序排列的GPS点组成,每个GPS点Pki包含经纬度和时间信息。
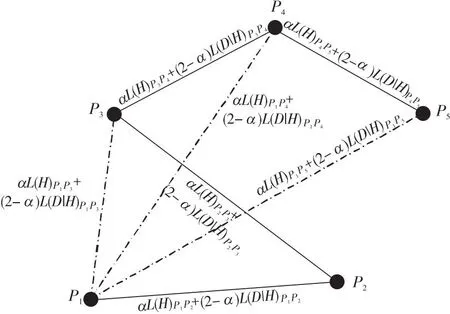
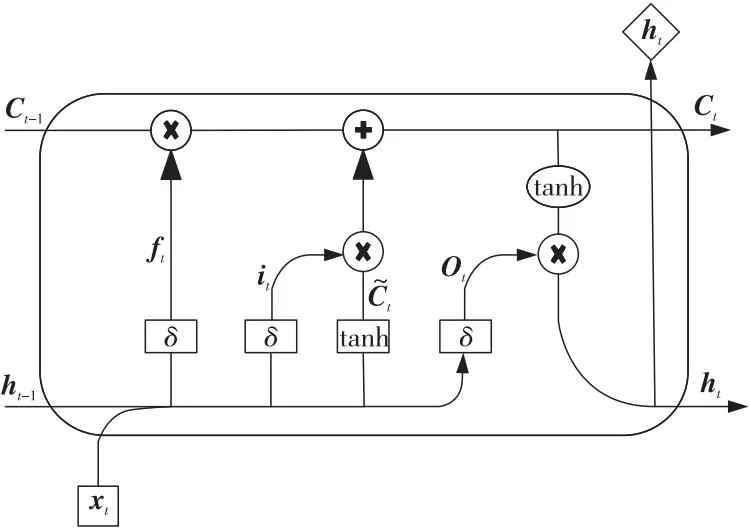
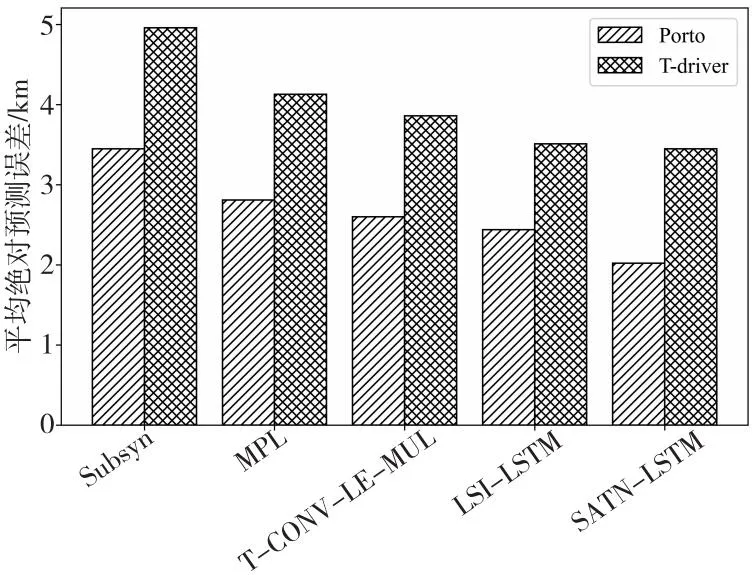
定义2(前缀轨迹序列Tf)Tf={Pk1,Pk2,…,Pki}(2 定义3(轨迹网格序列GT) 轨迹点所在的网格称为该轨迹点的轨迹网格,轨迹网格代替轨迹序列中的所有轨迹点形成的新序列称为轨迹网格序列GT={G1,G2,…,Gn}。 定义4(轨迹完成比例) 将分段后的轨迹看做完整轨迹序列,前缀轨迹序列占完整轨迹序列的比重,即Tf/Tk,称作轨迹完成比例。 定义5(轨迹目的地预测) 给定前缀轨迹序列Tf={Pk1,Pk2,…,Pki}(2 轨迹数据处理的整体流程如图1所示,首先对原始轨迹进行分段处理,详见3.2节;然后对分段后的轨迹进行网格划分和分布式表示,详见3.3和3.4节;最后对训练集轨迹的目的地进行聚类并添加伪标签,详见3.5节。 Figure 1 Overview of trajectory data processing图1 轨迹数据处理流程 经过处理后,最终得到以向量表示的轨迹数据以及具有标签的训练集。 由于位置设备的采样周期较短,收集到的位置数据多且连续,为了方便处理轨迹数据,需要对收集到的轨迹数据进行分段处理。轨迹数据分段是指在轨迹序列中找出某些属性值变化较大的特征点,根据特征点对轨迹进行分段。 为了得到最佳轨迹分段,本文提出了权重化最小描述长度WMDL(Weighted Minimum Description Length)的轨迹分段方法。将原始轨迹看作数据D,原始轨迹分成的段看作假设H,αL(H)表示假设的轨迹长度,(2-α)L(D|H)表示在此假设的前提下原始轨迹的权重化最小描述长度,当αL(H)+(2-α)L(D|H)最小时的假设H被称为能够描述原始轨迹的最优假设,此时的分段即为轨迹的最佳分段。其中,α为权重参数(0<α<2,α∈R),可通过调节权重参数α的值在简洁性和准确性之间进行取舍。当L(H)所占权重小于L(D|H)时,分段的准确性更高,适用于数据量较小的情况;当L(H)所占权重大于L(D|H)时,分段的简洁性更高,适用于数据量较大的情况。L(H)和L(D|H)的计算方法分别如式(1)和式(2)所示: (1) 1)+lb(dθ(PcjPcj+1,PkPk+1)+1)] (2) 其中,pari表示第i条原始轨迹段的长度,len(·)用于求解2个轨迹点之间的距离,cj表示当前原始轨迹的第j个轨迹点的编号,P*表示轨迹点,d⊥表示2个轨迹点连成的线段与另外2个轨迹点连成的线段之间的欧氏距离,dθ表示一条线段相对于另一条线段成锐角的相对距离。 对于任意轨迹T,第1步计算T中任意2个点之间的αL(H)+(2-α)L(D|H),将计算出的值作为这2个点之间的权重;第2步求出P1点到其它各点之间的权重之和,权重之和最小的点可作为整条轨迹的关键点,然后按此关键点进行分段;第3步把关键点之后的后一个点看作P1点,重复第2步和第3步,直至轨迹分段完毕为止。轨迹分段示例如图2所示,其中,实线为真实轨迹,虚线为近似轨迹,利用WMDL方法进行轨迹分段的过程可以看作求解无向完全图的最短路径问题。 Figure 2 Trajectory segmentation example using WMDL图2 基于WMDL的轨迹分段示例 对于分段后的轨迹,除时间戳和经纬度外,没有额外的辅助信息,为了克服数据稀疏问题,本文采用geohash算法对轨迹进行网格划分,轨迹网格划分的核心思想是把移动对象的活动范围看作一个矩形平面,然后用网格对该平面进行分割,以网格编码代替网格内轨迹点的经纬度信息。 按精度需求对所在区域进行网格分割后对网格进行编码,纬度分割遵循上1下0的原则,经度分割遵循左0右1的原则对经纬度依次进行分割,直到满足精度需求为止;然后将由二进制组成的网格编号从右向左进行32进制的Base32编码(0~9,b~z,去除a,i,l,o)。如轨迹点(-8.610 88, 41.145 57),编码长度设为7时所映射到的网格编码为ez3fh43。 在将轨迹序列进行网格划分后,由于相邻的轨迹点采样频率高而导致距离较近,可能会发生多个相邻轨迹点映射到相同的网格内的情况,从而造成网格编码序列的冗余。为了解决该问题,本文提出了序列偏移算法来去除冗余数据,序列偏移算法是根据轨迹编码序列G向右移位产生序列S,通过对比序列G和序列S对应位置是否相同来判断序列是否冗余。如果对应位置相同则产生冗余,为判断序列K相应位置赋值0;如果对应位置不相同,则未产生冗余,为判断序列K相应位置赋值1。最后根据判断序列K,生成非冗余序列G′;若判断序列K某个位置上为1,则将G中对应位置的值赋值给G′,若判断序列K某个位置上为0,则不为G′赋值,由此可得到去除冗余数据的编码序列G′。 将分段后的二维轨迹序列抽象表示为一维的网格编码序列,简化了轨迹序列的表示,然而网格编码序列属于字符串型数据,不能直接输入到模型中进行训练。虽然常用的独热码(One-Hot Encoding)能将其转化为向量,但是面对数量巨大的网格时会导致维度灾难,且独热编码也不能反映出网格之间实际的地理拓扑关系。 针对上述问题,本文提出了Base2vec模型,它是由小型多层感知机网络构成的,采用无监督的学习方法,能在历史轨迹中学习网格之间的实际地理拓扑关系,距离越近的网格,表征后的向量越相似。 对于网格编码表征任务而言,需要低维的表示以及保留网格之间的地理拓扑关系这2点要求,因此本文采用与Skip-gram类似的方法对轨迹的网格编码序列进行表征,如图3所示。其中,Gg表示当前网格的独热码,维度为M,N表示隐藏层的神经元的个数(N≪M)。在正向传播的过程中,输入向量与嵌入矩阵WM×N相乘得到隐藏层神经元的值;再通过与解码矩阵W′N×M相乘输出一个M维的向量,每一维均与一个网格编码相对应;最后利用SoftMax函数计算出与当前网格相似度最大的前k个网格编码,并将其与真实值进行对比,反向传播调整嵌入矩阵和解码矩阵的权重以得到最佳参数。最终目的是输入已知的轨迹点Gg,使模型预测结果为该轨迹点的上下序列的概率p(tra(Gg)|Gg)的乘积最大,目标函数如式(3)所示: (3) 其中,T表示所有轨迹点,tra(Gg)表示与Gg相邻的轨迹点。 Figure 3 Structure of Base2vec network图3 Base2vec网络结构 此时的嵌入矩阵即为最佳的映射矩阵,此后将每一个网格的独热编码与该嵌入矩阵相乘即可获得低维且蕴含地理拓扑关系的位置向量。 为了验证Base2vec模型的有效性,本文将编码为ez3fhk的网格作为测试网格输入到调整好参数的Base2vec模型中,此时输出与网格“ez3fhk”相似度最大的8个网格与该网格的地理拓扑关系如图4所示。根据实验结果可知,Base2vec存在微小的误差,但整体上保留了网格之间的地理拓扑关系。 Figure 4 Base2vec training effect visualization图4 Base2vec训练效果可视化图 根据历史轨迹和查询轨迹的匹配契合度来预测当前轨迹最有可能的目的地时可能会出现以下3种特殊情况:(1)不同起点的轨迹终点相同;(2)相同起点的轨迹终点不同;(3)相同起点和终点的轨迹相似度不同。因此,根据匹配契合度来预测目的地具有一定的局限性。由于经纬度属于连续性数值,并且历史轨迹数量和可用于辅助预测的附加信息有限,直接对查询轨迹的目的地经纬度坐标进行预测可行性不高,具有很大的预测难度。 为了提高预测任务的可行性,降低预测难度,本文对预测任务进行了如下改进: Step1提取训练集中所有轨迹的目的地并对其进行Mean Shift聚类,将目的地分为多个密集簇,记录每个簇的聚类中心。 Step2将聚类中心坐标按3.3节和3.4节的方法转化为包含位置信息的嵌入向量。 Step3以Step 2的结果作为标签,分别给对应的分布式表示后的轨迹进行标记。 以上改进将无监督训练的移动轨迹目的地预测转化为有监督训练的分类问题,很大程度上提高了任务的可行性。 SATN-LSTM轨迹目的地预测模型主要包含轨迹处理、LSTM、自注意力机制、Softmax分类器和geohash解码器5个模块,如图5所示。轨迹处理模块对原始轨迹进行分段和网格划分并通过Base2vec模型将其转化为神经网络可以处理的向量形式,同时赋予向量之间实际的地理拓扑关系;LSTM模块对向量进行特征提取;自注意力模块根据每个时间步提取特征对预测结果的影响来进一步分配特征权重,然后通过Softmax函数对其进行分类,最后将可能性最大的目的地聚类中心通过geohash解码器反解出经纬度坐标,该经纬度坐标即为预测结果。 Figure 5 Prediction model of moving trajectory destination图5 移动轨迹目的地预测模型 经过处理后,轨迹序列被表示为包含地理拓扑关系的嵌入向量,之后将其按照时间的先后顺序依次输入LSTM网络中进行特征提取。LSTM的神经元如图6所示,其中,ft、it和Ot分别表示t时刻的遗忘门、输入门和输出门,Gt表示t时刻的长期记忆的细胞态,Ct表示等待存入长期记忆的候选态。表示位置的嵌入向量在LSTM中的更新过程主要包括以下4个步骤: (1)将上个时间步中提取的表示位置的特征选择性遗忘。控制上个时间步提取的特征对当前细胞态Ct的影响程度,该过程由当前时刻的输入和上个时刻的输入共同决定,计算公式如式(4)所示: ft=σ(Wf·[ht-1,xt]+bf) (4) 其中,σ(·)表示Sigmoid激活函数,作用是把结果控制在0~1,Wf表示遗忘门的待训练参数矩阵,bf表示遗忘门的待训练偏置项,ht-1为t-1时刻的输出,xt为t时刻的输入。 (5) 其中,Wc和Wi表示输入门的待训练参数矩阵,bi和bc表示输入门的待训练偏置项。 Figure 6 Structure of LSTM neuron图6 LSTM神经元结构 (3)更新表征长期记忆的细胞态Ct。通过遗忘门和输入门的筛选,将需要保存的特征存入细胞态Ct,完成特征的更新,更新公式如式(6)所示: (6) 其中,it表示t时刻的总输入信息,Ct-1表示t-1时刻的细胞态。 (4)将细胞态中的特征选择性地进行输出。输出门对Ct中的特征进行选择性输出,再与经过tanh函数处理的Ct相乘得到当前时间步的输出ht,计算公式如式(7)所示: (7) 抽象化表示的前缀轨迹序列经过LSTM网络后得到t时刻的输出特征Ot以及表征整个前缀轨迹的总输出特征ht。 LSTM网络的输入是按时间步依次进行的,对于距离较远且关系密切的特殊点,需要经过多个时间步迭代才能联系到一起,这种联系会随着距离的增加而减小。因此,本文将自注意力机制引入LSTM网络中,通过计算每个时间步输出特征之间的关系,为各个特征分配相应的权重,能够很好地解决远距离轨迹点之间的特征依赖关系,计算过程如图7所示,共包括3个阶段。 Figure 7 Calculation process of weight allocation图7 权重分配的计算过程 第1个阶段将每一个特征中的查询Q和其它所有特征的键K进行相似度计算得到权重分值。相似度计算常用的方法有向量点积、余弦相似度或构建神经网络,本文采用向量点积来求权重分值,如式(8)所示: (8) 其中,Q和K表示某个输入x(对应图7中的x1,x2,…,xn)进行不同线性变化之后的结果,dx为特征向量x的维度。 由于第1阶段计算的权重分值的取值范围不固定,因此本文第2阶段引入Softmax函数对第1阶段的权重分值进行数值转换,如式(9)所示。此方法不但可以将所有特征的权重分值进行归一化处理,而且还能突出重要特征的权重。 (9) 第2阶段计算的结果即为每个特征向量对应的权重系数,因此第3个阶段将与其对应的值V进行加权求和后的结果即为当前轨迹序列的抽象表示,如式(10)所示: (10) 由于3.4节对轨迹添加了伪标签,因此本文将自注意力机制提取出的特征通过Softmax函数进行分类,即将该轨迹分类到其所属的簇中,以实现目的地的预测。在实际部署在线预测系统中,为了提高命中率和预测的精度,可以输出前k个可能性较高的目的地以作为参考,计算公式如(11)所示: (11) 其中,cx表示轨迹目的地的聚类中心,Zl表示轨迹序列l的抽象表示。 “各学段的阅读教学都要重视朗读和默读。加强对阅读方法的指导,让学生逐步学会精读、略读和浏览。”(小学语文课程标准)告诉我们默读既是教学目标,也是阅读教学中的一个非常重要的方式方法。因此,教科书从二年级下学期,一般在中段起,开始安排默读的训练。可笔者却惊讶的发现,在笔者所接触的语文教师的课堂中,平均默读时间每节课大约2-3分钟,有的甚至根本没有设计默读时间;所在学校学生的默读能力普遍较差,甚至到了高年级还不知道怎样默读。默读如此被忽视,与当前在小学语文阅读教学中较普遍重视朗读教学有关。而教师侧重朗读教学则源于新课程倡导让学生动起来,让课堂活起来。 最终预测的目的地为向量表示,通过geohash解码器将其反解为经纬度表示,该过程即为Base2vec和geohash编码的逆向过程。 本文使用2个真实的出租车轨迹数据集Porto和T-driver来验证提出模型SATN-LSTM的有效性和效率,并与Subsyn[18]、MLP[17]、T-CONV-LE-MUL[7]和LSI-LSTM[13]模型进行比较,以证实SATN-LSTM模型具有更高的准确性。 Porto数据集收录了葡萄牙波尔图市442辆出租车2013年全年的行车轨迹,共170多万条完整的行程。本文从数据集中随机选取10万条轨迹作为实验数据,经分段处理后共得到164 862条轨迹,按照20%~80%的轨迹完成比例对这些轨迹进行随机截取,将其中的60%作为训练集,20%作为验证集,另外的20%作为测试集。 T-driver数据集收录了北京市10 357辆出租车2008年2月2号到2008年2月8号一周的行车轨迹,约1 500万个轨迹点,轨迹总距离达到了900万公里。随机选取其中2 000辆出租车的完整轨迹,经分段处理后得到222 047条轨迹,剩余处理方法与Porto一致。 对比模型的介绍如下: (1)Subsyn[17]:该模型利用马尔科夫链模型建立每条轨迹中位置之间的转移关系,并遵循贝叶斯推理框架。 (2)MPL[18]:该模型是一种基于多层感知机的神经网络模型。输入层接收带有相关上下文信息的前缀轨迹表示,并采用标准隐藏层来训练轨迹。 (3)T-CONV-LE-MUL[7]:该模型采用多尺度多范围的卷积神经网络(CNN)模型。输入层接收转化为黑白图像的前缀轨迹表示,对目的地进行聚类并为图像添加伪标签,将目的地预测问题转化为图像分类问题。 (4)LSI-LSTM[13]:该模型在长短期记忆网络中引入注意力感知模块,输入层接收前缀轨迹表示,并反向传播更新参数。 定义6(平均绝对预测误差MAPE(Mean Absolute Prediction Error)[7]) 平均绝对预测误差是指预测目的地经解码后与真实目的地之间距离的平均值(单位为km),能直观反映出预测效果。计算公式如式(12)所示: (12) (13) (14) 定义7(平均相对预测误差MRPE(Mean Relative Prediction Error)[12]) 由于平均绝对预测误差比较苛刻,且在预测之前将轨迹映射到了相同大小的网格之中,因此本文引入平均相对预测误差来量化预测的偏离度,计算公式如式(15)所示: (15) 本文采用6位编码对分段后的轨迹进行网格划分,网格大小约为610 m×610 m,Porto数据集共生成225 106个网格,T-driver数据集共生成310 866个网格。 根据式(11),SATN-LSTM模型可以输出前k个最有可能的目的地。预测误差取前k个可能性最大的预测目的地到真实目的地的最短距离,k值的取值范围与平均绝对预测误差之间的关系如图8所示。由图8可知,较大的k可以很明显地降低预测误差,因为k值越大,输出预测目的地的数量就越多,命中真实目的地的概率相对也就越大。在T-driver数据集上预测误差随k值的增大下降较为明显,而Porto数据集上预测误差随k值的增大下降并不明显。经过对数据的分析可知,T-driver数据集相比Porto数据集更加复杂,预测精度也不及Porto数据集上的高,因此在T-driver数据集上随着k值的增大,预测误差下降较为明显。 Figure 8 Relationship between parameter k and prediction error图8 参数k和平均绝对预测误差之间的关系 当k大于5时,Porto和T-drive数据集上的预测误差下降态势趋于平缓,因此综合开销与收益考虑,在实际部署在线预测系统中将k的值取5,即可以使用前5个预测的目的地进行基于位置的推荐,以提高命中的概率。 将训练集、测试集和验证集中的轨迹序列转化为带有地理拓扑关系的向量表示,然后将训练集输入到模型中进行训练,用验证集调整模型参数,经多次调整后模型最优参数值如表1所示。最后根据预测评价指标对测试集的预测结果进行对比,并与Subsyn、MLP、T-CONV-LE-MUL和LSI-LSTM等现有的模型在相同的数据集上进行比较,这些模型均采取离线训练在线预测的方式。实验结果如图9和图10所示,在2种评价指标上,本文模型相较于Subsyn、MLP、T-CONV-LE-MUL等预测模型总体预测精度具有显著的提升,相较于LSI-LSTM模型在Porto数据集上具有显著优势,而在T-driver数据集上优势并不明显。根据对数据集的分析发现,相较于Porto,T-driver中轨迹数据的时间跨度较短,并且不同轨迹之间的空间距离跨度较大,轨迹数据相较于Porto数据集更加复杂和多样化,且LSI-LSTM模型也具有较高的准确性,因此在T-driver数据集上相较于LSI-LSTM模型预测精度提升有限。 Table 1 Model parameters表1 模型参数 Figure 9 MAPE of different models图9 不同模型的平均绝对预测误差 Figure 10 MRPE of different models图10 不同模型的平均相对预测误差 在轨迹数据处理方面,Subsyn模型将子轨迹进行合成,通过增加轨迹数量的方式来解决数据稀疏问题;MPL模型将子轨迹转化为不包含地理拓扑关系的向量表示;T-CONV-LE-MUL模型则是将子轨迹映射为二维图像,但粒度选择困难;LSI-LSTM模型把更多的语义信息融入子轨迹网格向量中,却没有考虑轨迹网格之间的地理拓扑关系。在轨迹的处理和表示方面都存在诸多不足,本文提出的轨迹分布式表示方法尽可能地弥补了现有方法的缺点。在预测方法方面,Subsyn和MLP模型没有考虑轨迹的长期依赖问题;T-CONV-LE-MUL模型只截取了轨迹的开始和结束位置的部分轨迹,有很大程度的局限性;LSI-LSTM模型的注意力感知模块参数较多,导致调整困难;本文将自注意力机制融入LSTM网络中,挖掘序列中的关键点并根据其重要程度分配权重,较好地解决了长期依赖问题。根据实验结果可知,本文提出的预测模型和轨迹处理方法具有更好的性能表现。 除了上述验证外,本文在固定轨迹完成比例的情况下也进行了相关实验,引入轨迹完成比例的概念以测试各模型在不同轨迹完成比例下的预测性能,从多角度验证模型的鲁棒性。固定轨迹完成比例分别取10%~80%,在Porto和T-driver数据集上对固定轨迹完成比例的轨迹进行实验验证,实验结果如图11和图12所示。 Figure 12 MAPE on T-driver dataset图12 T-driver数据集的MAPE 随着轨迹完成比例的增加,所有模型的预测误差都是逐步下降的,即前缀轨迹越接近目的地,可提供的轨迹信息越多,预测结果也就越准确。与此同时,本文模型相较于LSI-LSTM等模型在较短的轨迹完成比例下更具优势,尤其是在20%的轨迹完成比例下具有明显的优势,证明了自注意力机制较好地解决了长期依赖问题。此外,结合图9和图10,相较于现有的预测模型,在混合轨迹完成比例和固定轨迹完成比例下,本文提出的模型相较于其它模型都有更好的表现。 轨迹的目的地预测在智能交通系统、智能导航系统和推荐系统等领域具有广泛的应用。本文提出了一种基于LSTM网络的移动轨迹目的地预测模型,对轨迹进行网格划分,用Base2vec对轨迹进行分布式表示,缓解了数据稀疏问题带来的影响。针对长期依赖问题,引入了自注意力机制,通过计算LSTM网络任意2个时间步输出之间的相关关系,为每个输出分配相应的权重。之后的工作将考虑在轨迹信息中嵌入时间、车辆ID等更多的语义信息,通过这些信息来加强前缀轨迹与真实目的地之间的联系,以提高预测的精度。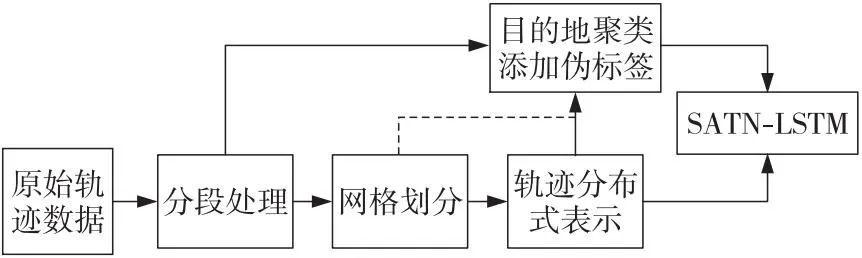
3.2 轨迹分段
3.3 轨迹网格划分
3.4 轨迹分布式表示方法


3.5 目的地聚类和伪标签添加
4 移动轨迹目的地预测模型

4.1 长短期记忆(LSTM)网络

4.2 自注意力机制

4.3 Softmax分类器和geohash
5 实验与结果分析
5.1 预测评价指标
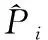
5.2 样本集生成及Top-k分析

5.3 不同模型预测结果对比


5.4 轨迹完成比例对预测结果的影响

6 结束语

