基于EOF的江苏省多年降雨和气温时空分布特征

周毓豪

(河海大学农业科学与工程学院，江苏 南京 210018)

0 引言

根据IPCC第六次评估报告，在全球大背景下，由于受到全球气候变化和“城市化”效应的双重影响，城市发生极端高温和热浪事件十分频繁，也更容易遭受洪水灾害，这对中国社会、经济造成巨大影响[1]。近些年来，受人类活动和气候变化的影响，中国大陆地区极端降雨事件的发生频率和强度均有所增加，并表现出明显的区域性[2]。Chen Zeqiang[3]等运用修正后的卫星降雨数据，通过频率分析研究区域极端降雨的时空特征，结果表明长江流域从上游到下游降雨量逐渐增加。梅梅[4]等研究气候变暖背景下，高温、复合极端事件将变得更为极端，特别在四川盆地东部和长江流域东南部最为显著。频繁发生的高温、热浪等事件将加重长江中下游地区的高温热害情况[5]。

江苏是中国的重要经济、工业、外贸大省，2022年末全省常住人口8515万人，新型城镇化建设步伐加快，年末常住人口城镇化率达74.4%[6]，城市的快速发展对气候变化有着直接而现实的影响。江苏地形以平原和丘陵为主，中部及南部为长江三角洲平原，东北部为山地丘陵区，东部为黄海，长江、太湖等重要河湖横贯全省，总体地形复杂多样，不同区域气候存在差异。本文通过对江苏省近73年降雨和气温数据进行EOF分解，分析不同区域气温和降雨的时空分布特征，为应对全球气候变化、实现江苏经济高质量发展提供参考。

1 资料及方法

1.1 资料

研究资料利用1950—2022年逐月的平均降雨和气温的栅格数据，数据来源于欧盟及欧洲中期天气预报中心等组织发布的ERA5-Land数据集，利用栅格计算公积计算12个月平均降雨和气温的平均值，得到江苏省逐年平均降雨和气温数据，然后进行EOF分析。

1.2 研究方法

经验正交函数分析方法(Empirical Orthogonal Function，缩写为EOF)，也称特征向量分析(Eigenvector Analysis)或者主成分分析(Principal Component Analysis，缩写PCA)，是一种分析矩阵数据中的结构特征，提取主要数据特征量的一种方法[7-8]。Lorenz在20世纪50年代首次将其引入气象和气候研究，该方法已在海洋和其他学科中得到了广泛的应用[9]。

EOF将时空数据分解为空间模态(EOF)和对应的时间系数(PC)，即X=EOFm×m×PCm×n，m为站点数，n为年数。为了保证各模态之间的独立性，North等的研究指出，在95%置信度水平下的特征根的误差为：

(1)

式中，λ—特征根；N*—样本的数量。

将λ按顺序依次检查，标上误差范围。如果前后两个λ之间误差范围有重叠，则没有通过显著性检验[10]。

2 年均降雨EOF模态分析

2.1 平均降雨年际变化

江苏省有13个地级市，长江以南的有5个市，长江以北的有8个市。为便于研究，本文以长江为界，利用各市逐年年均降雨资料分别计算出苏北地区、苏南地区和全省平均年降雨量，如图1所示。由1图可知，江苏地区年平均降雨量在1.5～6mm范围内波动，其中1954年达到极大值5.64mm，1978年达到极小值1.93mm，苏南地区平均降雨量整体高于苏北地区。

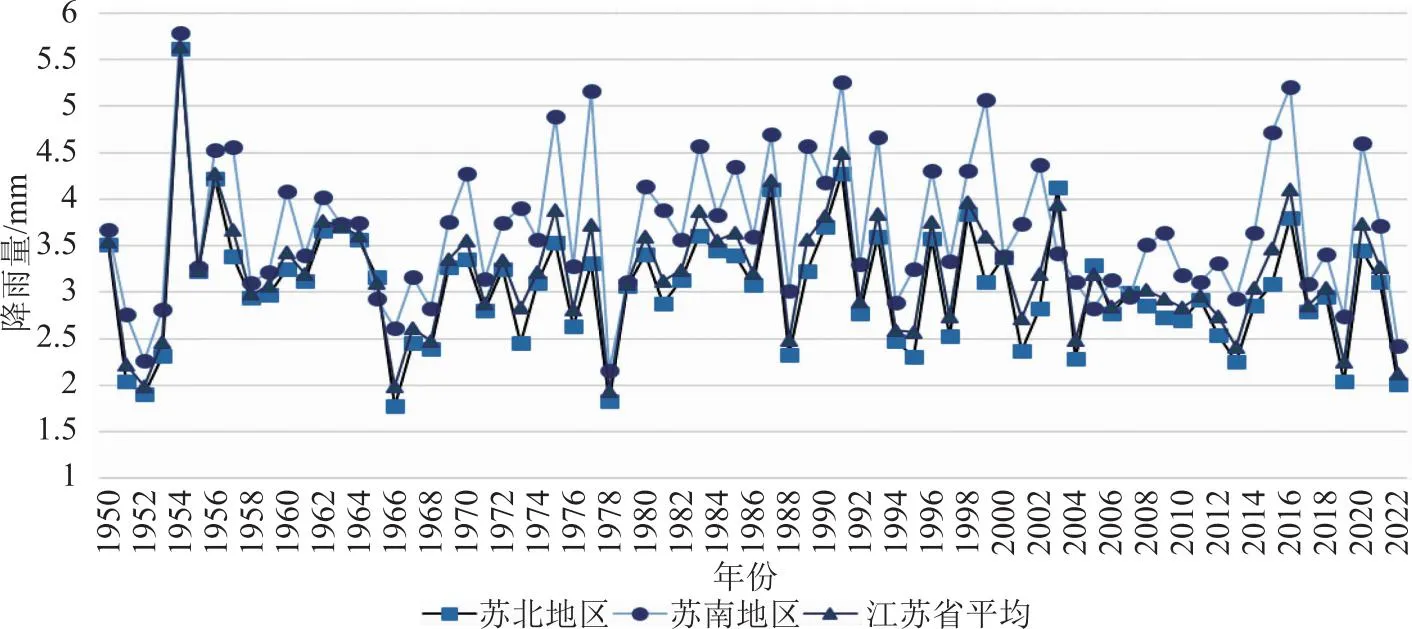
图1 1950—2022年江苏省年平均降雨变化图

2.2 年均降雨EOF分析

据表1显示，前4个特征向量的特征根、方差贡献及特征根误差范围反映了1950—2022年江苏年均降雨的2种空间分布类型：全区多(少)型、北多(少)南少(多)型。虽然前4个特征向量的累积方差贡献率达到96.07%，但是只有前2个特征根的误差(累积方差贡献率90.07%)通过North显著性检验。因此，这2个特征向量能基本反映部分地区的年均降雨情况。

表1 1950—2022年江苏省年平均降雨EOF分析方差贡献率

降雨EOF第一模态的方差贡献率为73.54%，反映了年平均降雨分布的最主要典型场。根据图2(a)可以发现降雨EOF第一模态为正，表明年平均降雨呈现整体一致性，即全区多雨或全区少雨的特征。该模态的高值区域分布在宁镇扬中部、常州、无锡等地区，说明该区域对降雨的敏感度较高。

图2 1950—2022年江苏省年平均降雨EOF分析

降雨EOF第二模态的方差贡献率为16.53%。

由图2(b)可见，大致以长江以北为界，向北为正值区，向南为负值区，正值中心位于淮安、宿迁等地；负值中心位于苏锡常地区。整体雨型表现为南北反相位特征，即江北地区降雨偏多时，江南地区偏少；反之，江北地区降雨偏少时，江南偏多。研究结果与夏露[11]等的研究结论相一致。

2.3 年均降雨时间分布

图3显示出江苏年均降雨前2个特征向量对应的时间系数，其正负号对应特征向量的方向，系数绝对值与该时刻降雨空间分布类型的典型性呈正相关。

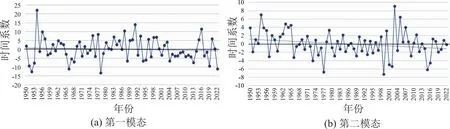
图3 1950—2022年江苏省年平均降雨EOF分析时间线

分析降雨EOF第一模态的时间系数如图3(a)所示，其斜率略小于0，说明1950—2022年江苏地区整体降雨量有减小趋势。其中1950—1990年年均降雨量呈增加趋势，1991—2022年年均降雨量呈减少趋势。32年的时间系数为正值，同时与降雨EOF第一模态的正向空间分布相吻合，表明江苏整体偏向湿润，尤以宁镇扬中部、常州、无锡等地区最为明显，时间系数正值越大，对应年份的降雨量越大，以1954年的情况最为明显。其余40年时间系数为负，其绝对值越大，对应年份的降雨量越少，空间上苏北地区，如徐州地区降雨量最少。

根据图3(b)可以看出降雨EOF第二模态时间系数的斜率小于0，说明1950—2022年江苏地区整体降雨量呈减少趋势，而江北地区降雨量有一定的增加趋势。在图3(b)中，时间系数为负的有47年，其降雨位相与图2(b)相反，空间分布呈北多南少。降雨量逐渐增加，典型年份为1999年。时间系数为正的年份有26年，其呈东南干西北湿，典型年份为2003年。

综合EOF第一、第二模态及对应时间系数，江苏省降雨量以长江为界，南北差异显著，在1950—1990年呈略增加趋势，1991—2022年呈减少趋势，全省整体降雨量近73年呈减少趋势，这与夏露[11]等的研究结论不一致，主要原因可能与城市化发展造成的“热岛效应”有关，也可能与样本数量不一致的影响。

3 年均气温EOF模态分析

3.1 平均气温年际变化

利用各市逐年年均气温资料分别计算出苏北地区、苏南地区和全省平均年气温值，如图4所示。由图4可知，江苏地区年平均温度在13.5～17.5℃范围内波动，其中2007年达到极大值16.3℃，1968年达到极小值13.95℃，苏南地区平均温度整体高于苏北地区。1950—1993年，江苏地区平均气温在15℃上下波动，1993年以后平均气温在16℃上下波动，1993年以后全省年平均气温上升约1℃，说明在30年内气温明显变暖。

图4 1950—2022年江苏省年平均气温变化

3.2 年均气温EOF分布

据表2显示，前4个特征向量的特征根、方差贡献以及特征根误差范围反映了1950—2022年江苏年均气温的2种空间分布类型：全区热(冷)型、北热(冷)南冷(热)型。虽然前4个特征向量的累积方差贡献率达到99.6%，但是只有前2个特征根(累积方差贡献率98.76%)通过North显著性检验。因此，这2个特征向量能较好反映江苏部分地区的年均气温情况。

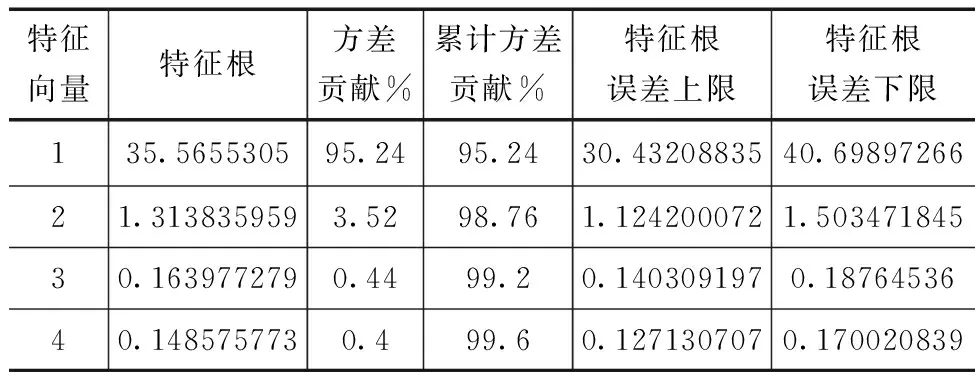
表2 1950—2022年江苏省年平均气温EOF分析方差贡献率

气温EOF第一模态的方差贡献率为95.24%，反映了江苏年平均气温分布的最主要典型场。图5(a)显示降雨EOF第一模态为正，表明年平均气温变化趋势一致，即全区气温分布要么整体偏高要么整体偏低。高值区位于徐州、淮安和宿迁地区，表明该区域气温变化活跃度高。气温EOF第二模态的方差贡献率为3.53%，由图5(b)可见，大致以长江以北为界，向北为正值区，向南为负值区，正值中心位于淮安、宿迁等地，负值中心位苏锡常地区，表现与降雨第2特征向量极为相似，呈现出由北向南变化的趋势。

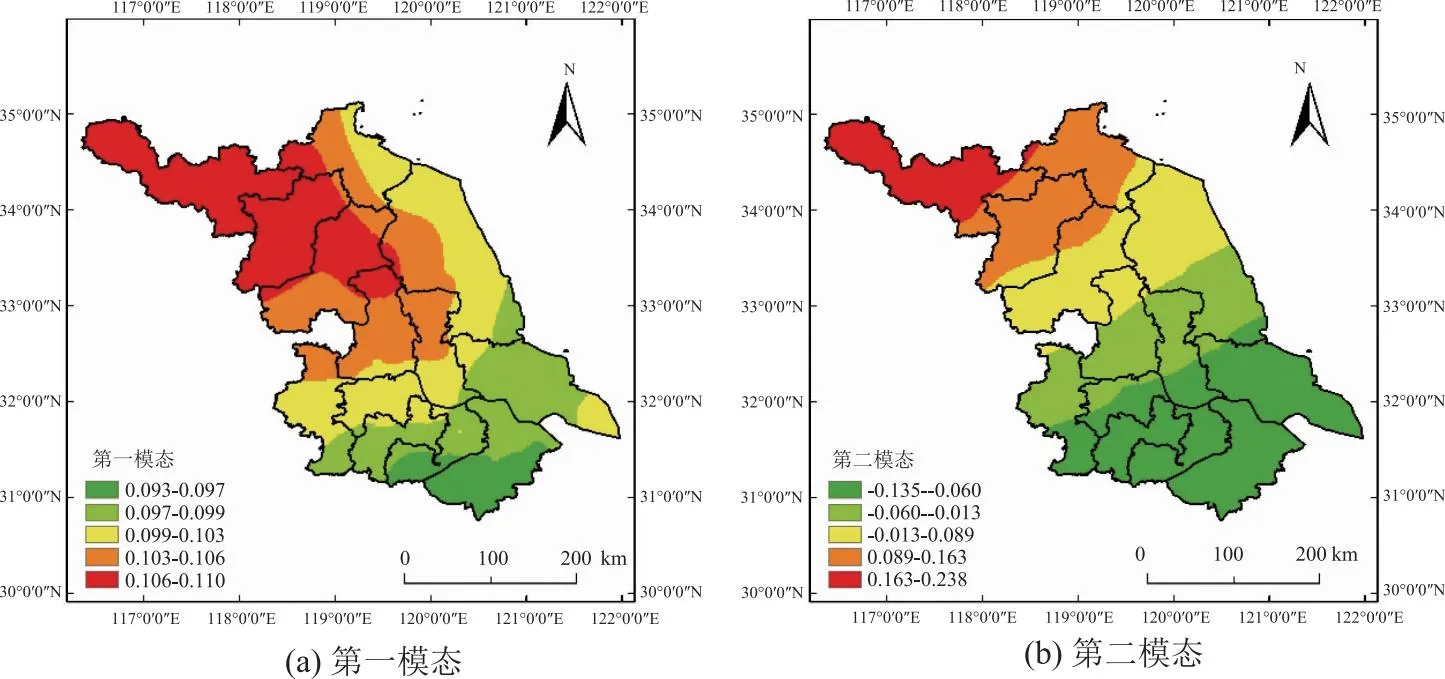
图5 1950—2022年江苏省年平均气温EOF分析

3.3 年均气温时间分布

年均气温EOF第一模态的时间系数，如图6(a)所示，由此分析得出1994年之前绝大部分年份时间系数为负值，1950—1994年江苏地区气温偏低；1995—2022年，时间系数逐年上升，几乎全为正值，该段时间内江苏地区气温偏高。纵观73年，江苏地区呈现明显的升温趋势。年均气温EOF第二模态对应的时间系数，如图6(b)所示，由此分析得出1950—1977年江苏地区气温年际变化较大，呈整体上升趋势；1978—2022年EOF第二模态时间系数呈下降趋势，其中1978—2002年为正值，反映在此期间江南地区气温低于江北地区，2003—2013年为负值，反映在此期间江南地区气温低于江北地区，2014—2022年波动较小，说明江南江北地区的气温差异趋于平衡。

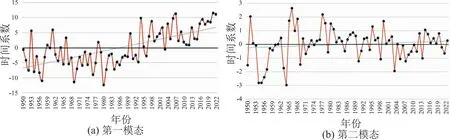
图6 1950—2022年江苏省年平均气温EOF分析时间线

综合EOF第一、第二模态及对应时间系数，江苏省气温与时间正相关，呈逐年上升趋势，同时不同时期不同地区呈现出差异化，即1994年以前，整体气温偏低，气温增长率低；1994年以后，整体气温偏高，且气温增长率变高。江北地区在2002年前高于江南地区，在2003—2014年低于江南地区。

4 讨论

研究表明，快速的城市化会改变下垫面的构成，主要表现为地面植物的减少和水泥建筑的增加。与此同时，由于城市聚集地人口众多，人类生存所产生的二氧化碳等气体和汽车尾气等温室气体对城市气候也产生了很大影响[12]；城市地表温度呈现逐年增加趋势，热岛效应逐步向周围地区蔓延[13]。因此，城市化发展是江苏地区降雨、气温年际变化的一个重要原因。

自20世纪90年代以来，江苏省的城市化水平一直稳步发展，根据王益华[14]等的研究，江苏省的城市化发展分为4个阶段：开始阶段(1949—1969年)、稳定发展阶段(1970—1989年)、加速发展阶段(1990—2005年)、高速发展阶段(2006—2015)。这与降雨和气温EOF第一模态时间系数图有高度的相似性，降雨和气温的时间分布与该地区城市化发展进程具有一定关联。

其次，江苏省城市的空间分布主要从东南沿长江两岸和沿太湖地区城市聚集，向北减少，这与降雨和气温EOF第一模态空间分布图展示的相一致，说明江苏地区降雨和气温的空间分布与城市分布具有一定相关性。

5 结语

通过使用EOF方法分析了1950—2022年江苏省的降雨和气温数据，结果显示年平均降雨空间分布呈整体一致性，以长江以北为界分成江南、江北2个特征区，且年平均降雨存在南北反相位特征，全省整体降雨量近73年呈减少趋势，降雨量变化呈现出波动性[15]，全省气温与时间正相关，呈逐年上升趋势。江苏地区降雨和气温变化与城市化发展关系密切，在时间和空间上与城市化发展呈现出一定相关性，主要原因是城市化发展导致下垫面的改变[16]，从而影响地区降雨分布，同时城市“热岛”效应也会对地区气温变化产生影响。

通过对江苏省年平均降雨和气温的空间分布进行分析，可以更好地了解江苏省的气候变化情况，为气候监测和应对气候变化提供参考。通过对城市化发展对降雨和气温的变化的分析，有助于深入认识城市化进程对环境的影响，为城市规划和环境保护提供依据。本文研究存在不足之处：主要关注了江苏省的降雨和气温空间分布特征，但在其他方面如降水强度、降水类型等方面的研究较为不足，且只使用了EOF方法进行分析，对其他统计方法方面应用较少，可能导致结果具有一定局限性。