基于时间窗和多仓温控的生鲜商品配送车辆路径优化问题

王勇，王静媛，苟梦圆，罗思妤

绿色包装与循环经济

基于时间窗和多仓温控的生鲜商品配送车辆路径优化问题

王勇，王静媛，苟梦圆，罗思妤

（重庆交通大学，重庆 400074）

针对当前生鲜商品配送效率低和成本高等问题，采用车仓温度可控的多仓车辆作为配送装备，并结合时间窗等约束，研究基于时间窗和多仓温控的生鲜商品配送车辆路径优化问题。建立最小化物流运营成本和车辆使用数量的双目标模型，然后设计基于Clarke-Wright节约算法的非支配排序遗传算法（CW-NSGA-Ⅱ）求解该模型。利用CW节约算法生成初始配送路径，以提高初始解的质量，并设计精英迭代策略，以提高算法的寻优性能。基于改进的Solomon算例，将文中所提算法与多目标粒子群算法、多目标蚁群算法、多目标遗传算法进行了对比，验证了CW-NSGA-Ⅱ算法的求解性能。结合实例，对多仓车辆使用数量、温控成本和运营成本等指标进行对比分析，结果表明，经优化后多仓车辆使用数量减少了35.7%，温控成本减少了39.2%，物流运营总成本减少了47.7%。文中所提模型和算法能够有效优化配送路径，降低运营成本，为构建高效率、低成本的生鲜配送网络提供了理论支持和决策参考。

生鲜商品配送；多仓温控；时间窗；CW-NSGA-Ⅱ

近年来，随着电子商务的发展和人民生活水平的提高，生鲜商品配送服务逐步向高品质、精细化、个性化方向发展，客户不再局限于单一的商品需求[1]。然而，传统的生鲜配送方式通常采用单车仓冷藏车进行服务，无法一次性满足客户现阶段多种商品的需求，导致配送效率较低。此外，生鲜商品具有时效性、易腐性，不合理的配送路径规划（如交叉配送、远距离配送等）会延长配送时间，增大生鲜商品的腐坏概率，从而增加配送成本和温控成本。运输装备的合理选用和配送路径的有效规划直接关系到生鲜商品配送服务效率的提升和运营成本的降低。应用多仓配送车代替单仓配送车作为运输装备，通过合理设置不同车仓的温度、规划配送路径能够满足客户的多样化生鲜商品需求，并能够有效缩短配送距离和配送时间，提高配送服务效率，减少生鲜商品的损坏，因此研究基于时间窗和多仓温控的生鲜商品配送车辆路径问题对于推动生鲜配送行业的高质量发展具有重要意义。国内外学者从多仓配送车辆路径优化问题和生鲜商品配送路径优化问题两方面进行了一系列研究工作。

针对多仓配送车辆路径优化问题，20世纪80年代，Christofides等[2]以车辆路径问题变体的形式提出了多仓配送车辆路径优化问题。Coelho、Laporte[3]将多仓车辆路径问题分为4类，并针对每类问题建立了优化模型。孙丽君等[4]研究了不同横向转运方式下的成品油多仓配送路径优化问题，建立了配送成本最小化的数学模型，应用节约算法求解该模型，有效降低了企业的配送成本。Chen等[5]研究了易腐商品的多仓配送车辆路径问题，以包含固定成本和油耗成本的总成本最小化为目标，设计了自适应大邻域搜索算法。Ostermeier等[6]研究了零售商品配送问题，研究发现，相较于单车仓车队，使用包含单车仓和多车仓的混合车队进行配送，可以节约高达30%的运营成本。王淑云等[7]研究了随机需求下的蓄冷式多温共配问题，建立了总成本最小化模型，并分别设计了蚁群算法和动态规划算法。由上述文献可知，相较于单仓配送车辆，使用多仓配送车辆能够有效降低运营成本。在生鲜商品配送方面，如何合理规划多仓配送车辆路径有待进一步研究。

针对生鲜商品配送路径优化问题，李军涛等[8]构建了以配送总成本最小化和客户满意度最大化为目标的多车型路径优化模型，并采用自适应遗传模拟退火算法求解。Zulvia等[9]以运营成本、货损成本、碳排放量最小化和顾客满意度最大化为目标，设计了多目标梯度进化算法。梁桂云等[10]针对当前生鲜商品配送过程中成本高、配送效率低下和商品损耗大等问题，以新鲜度最大化和总成本最小化为目标，建立了生鲜商品配送联合调度优化模型，并使用非支配排序算法进行求解。Liu等[11]以配送成本和碳排放成本最小化为目标，建立了生鲜企业横向合作模式下的绿色车辆路径优化模型，通过模拟退火算法进行路径优化，显著降低了目标函数值。上述多目标函数构建和混合智能算法设计为研究基于时间窗和多仓温控的生鲜商品配送问题提供了切入方法。

基于以上情况，文中构建了最小化运营成本和配送车辆使用数量的双目标优化模型，设计了基于节约算法的非支配排序遗传算法求解模型。结合实例，对比分析了不同车仓数量下的运营成本、温控成本和车辆使用数量等指标，为带时间窗和多仓温控的生鲜商品配送车辆路径优化问题提供了新思路。

1 问题描述

针对客户多种温控区间的生鲜商品需求，多仓配送车从配送中心出发，为沿途的客户提供服务，服务完成后返回配送中心。多仓配送车可以为具有多种生鲜商品需求的客户提供服务，减少了配送次数和车辆使用数量。在车辆路径规划时，根据生鲜商品的类型，将其安排在合适温度区间的车仓和该车辆的配送路线中，从而减少温控成本，提高车辆的装载利用率。结合客户的地理位置、服务时间窗和生鲜商品需求类型等信息，合理规划多仓配送车辆路径，可减少配送车辆的使用数量，降低时间窗惩罚成本。基于时间窗和多仓温控的生鲜商品配送车辆路径优化前后对比如图1所示。

优化前的配送路径和车仓装载情况如图1a所示，在配送网络中路径交叉冗余、客户时间窗被违反的现象较多，部分多仓配送车的车仓装载商品较少、剩余空间较大，增加了车辆使用数量，提高了配送成本、时间窗惩罚成本。优化后的配送路径和车仓装载情况如图1b所示，根据网络中各个客户的生鲜商品需求，将同类温度控制区间的生鲜需求安排给同一多仓车辆进行服务，并合理规划该多仓车辆的路径，使其尽可能实现多仓满载，且减少客户的时间窗违反现象，进而降低配送成本和时间窗惩罚成本。

图1 基于时间窗和多仓温控的生鲜商品配送车辆路径优化前后对比

2 模型建立

2.1 模型假设

生鲜商品配送网络中包含1个配送中心、多辆多仓配送车和一系列客户点。配送中心根据客户的地理位置分布和生鲜商品需求数量、类型对多仓配送车进行配送调度[12]。模型假设如下。

1）多仓配送车辆均为同一车型，1辆车配备了多个车仓，每个车仓的空间划分相同，但每个车仓可设置不同的温度区间。

2）在配送过程中，不考虑车辆的导航路径及道路运输实际场景对车辆行驶速度的影响，并假定多仓配送车行驶速度相同且恒定[13]。

3）不考虑多仓配送车在客户点的服务时间。

4）客户时间窗惩罚成本由车辆到达客户点的时间和客户点需求量决定[14]。

2.2 符号定义

这里涉及的变量及其定义如表1所示。

2.3 模型构建

以物流运营成本1最小化和多仓配送车使用数量2最小化为目标，建立了基于时间窗和多仓温控的生鲜商品配送车辆路径优化模型，见式（1）～（2）。

表1 变量定义

Tab.1 Variable definition

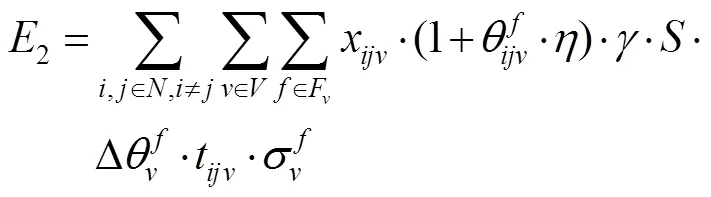
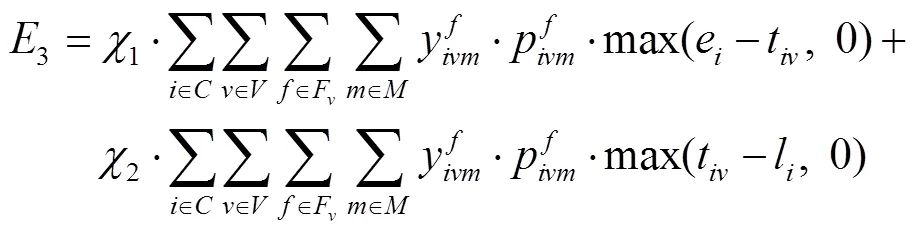
约束条件见式（8）～（20）。其中，式（8）表示每个客户只能被1辆多仓配送车访问1次。式（9）表示配送节点流量守恒。式（10）表示消除子回路。式（11）表示多仓配送车的使用数计算方式。式（12）表示车仓装载量不超过该车仓的最大载质量。式（13）表示任意一辆多仓配送车的行驶距离不超过该车辆的最大行驶距离。式（14）表示客户的每种生鲜商品需求只能由1辆多仓配送车中的1个车仓提供。式（15）表示多仓配送车到达节点的时间均在其服务时间窗内。式（16）～（17）表示多仓配送车到达节点的时间约束。式（18）～（20）表示决策变量约束。

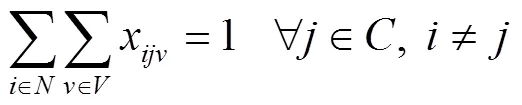
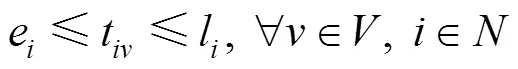
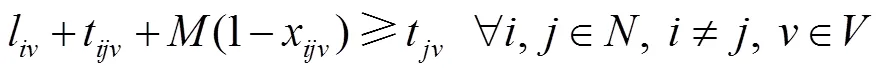
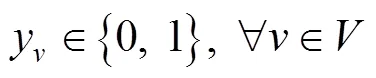
3 CW-NSGA-Ⅱ算法设计

这里设计了基于Clarke-Wright节约算法的非支配排序遗传算法，以求解基于时间窗和多仓温控的生鲜商品配送车辆路径优化问题。首先，利用Clarke-Wright（CW）节约算法生成初始路径。然后，应用非支配排序遗传算法（NSGA-Ⅱ）进行车辆路径的迭代优化，并引入精英迭代策略，从而提高算法全局寻优能力。最后，输出帕累托最优解集。CW-NSGA-Ⅱ算法流程如图2所示。其中，表示算法迭代次数，max表示算法最大迭代次数，表示精英迭代次数，max表示最大精英迭代次数。

图2 CW-NSGA-Ⅱ算法流程

3.1 初始种群构造

采用整数编码方式[17]构造染色体。假设该生鲜商品配送网络中共有6个客户，经过整数编码，染色体表示为（1，2，3，4，5，6）。根据约束对该染色体解码，可行解表达为（0，1，2，0，3，4，0，5，6，0），其中0表示配送中心。该可行解共有3条生鲜商品配送路径：配送路径1为0→1→2→0；配送路径2为0→3→4→0；配送路径3为0→5→6→0。初始种群的构造应用CW节约算法[18]，具体步骤如下。

1）将个客户分别与配送中心相连，构成个闭合回路0→→0（=1，2，3，…，）。

2）对于任意2个客户点组成的连接点对(,)，根据式（21）计算其节约里程值(,)。其中，c为节点与节点之间的距离。

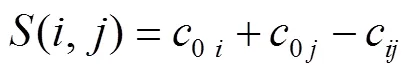
3）将所有(,)按降序排列。

4）设置1条空路径，根据(,)的排列顺序，逐个考察各客户连接点对(,)。若满足客户点和不在一条配送路径上且均与配送中心相邻，则将连接点对(,)插入路径中。当该路径违反载重约束或配送中心的时间窗约束时，则关闭该条配送路径，重新开启一条空路径。重复步骤4），直至所有客户被插入配送路径中。

5）输出初始种群。

3.2 部分映射交叉

部分映射交叉常被用于车辆路径问题求解，可有效避免算法陷入局部最优解[19-20]。首先，通过锦标赛选择2条父代染色体1和2，然后随机选择染色体上的基因位置作为交叉区域进行局部交叉，最后进行冲突测试。如果染色体中出现基因重复，则根据交换的基因片段建立映射关系，从而保证子代基因无冲突。部分映射交叉操作如图3所示。

由图3a可知，染色体1和2执行部分映射交叉后，生成染色体1、2。对1、2解码后生成配送方案。其中，1中有2条配送路径，分别为：0→3→5→0，0→1→6→4→2→0；2中有2条配送路径，分别为：0→2→4→1→0，0→3→5→6→0。

3.3 多点变异

通过锦标赛选择、部分映射交叉操作后，利用多点变异扩大解空间[21]。首先根据变异概率选择父代染色体，然后在选出的父代染色体中随机选择2个基因进行交换，剩下的基因再随机生成，最后检查染色体中是否存在重复基因，若“是”，则移除重复基因后再生缺失基因。多点变异操作如图4所示。

图3 部分映射交叉操作示意图

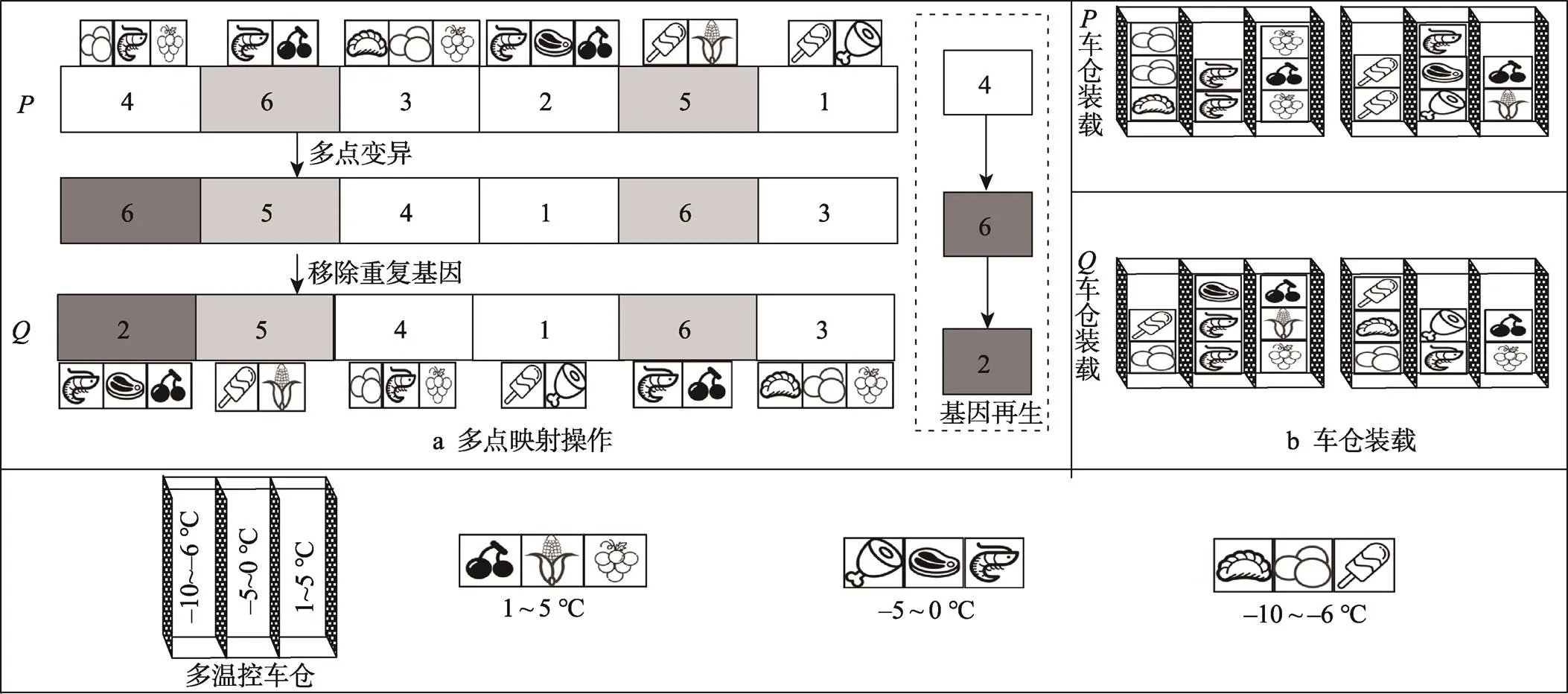
图4 多点变异操作示意图

3.4 帕累托优化解选择

帕累托优化解的选择主要依据解的非支配层级及拥挤度[22]，非支配层级={1,2,3, …,}，具体步骤如下。

1）对种群中每个个体设置2个参数、，其中表示种群中支配个体的解数量，表示被个体所支配的解集合。

2）设置=1，将=0的个体归入。

3）对于中的每个个体，遍历其所支配的解集，将中每个个体的减去1。

4）令=+1，将=0的解归入。

5）重复步骤3）、4），直至所有个体均被划分等级。

为了衡量同一层级中个体的优劣，将每层级边界上个体的拥挤度设置为无穷大，利用式（22）、（23）计算各层级中剩余个体的拥挤度。

帕累托优化解的选择过程如图5所示。种群中个体的非支配层级优于个体的非支配层级，所以个体优于个体；个体与个体处于同一非支配层级中，但个体的拥挤度大于个体的拥挤度，则个体优于个体。

3.5 算法比较

为了验证CW-NSGA-Ⅱ算法的有效性，将CW- NSGA-Ⅱ算法与多目标粒子群算法（MOPSO）[23]、多目标蚁群算法（MOACO）[24]、多目标遗传算法（MOGA）[25]进行对比分析，算法的相关参数设置如表2所示。

图5 帕累托优化解选择

在Solomon数据集[26]中选取15组数据进行改进，增加了客户需求的生鲜商品种类及质量，算例数据特征如表3所示。每组算例分别计算10次，选取最优物流运营成本、多仓配送车使用数量和求解时间进行对比，具体结果如表4所示。

如表4所示，首先在运营成本方面，CW-NSGA-Ⅱ算法计算结果均值为14 424.5元，相较于MOPSO、MOACO、MOGA，分别降低了11.7%、10.3%、11.2%；其次，在多仓配送车辆使用数量方面，相较于其他算法，CW-NSGA-Ⅱ的计算结果均值减少了1辆；最后，在算法求解时间上，CW-NSGA-Ⅱ的平均求解时间为164.9 s，而MOPSO、MOACO、MOGA的平均求解时间分别为175.2、174.0、175.4 s。通过检验与比较，结果显示，CW-NSGA-Ⅱ算法与其他3种算法存在显著性差异。由此可见，在求解文中所研究的问题方面，CW-NSGA-Ⅱ算法具有更好的寻优能力。

表2 算法参数设置

Tab.2 Parameter settings

表3 算例数据特征

Tab.3 Characteristics of the datasets

表4 不同算法优化结果对比

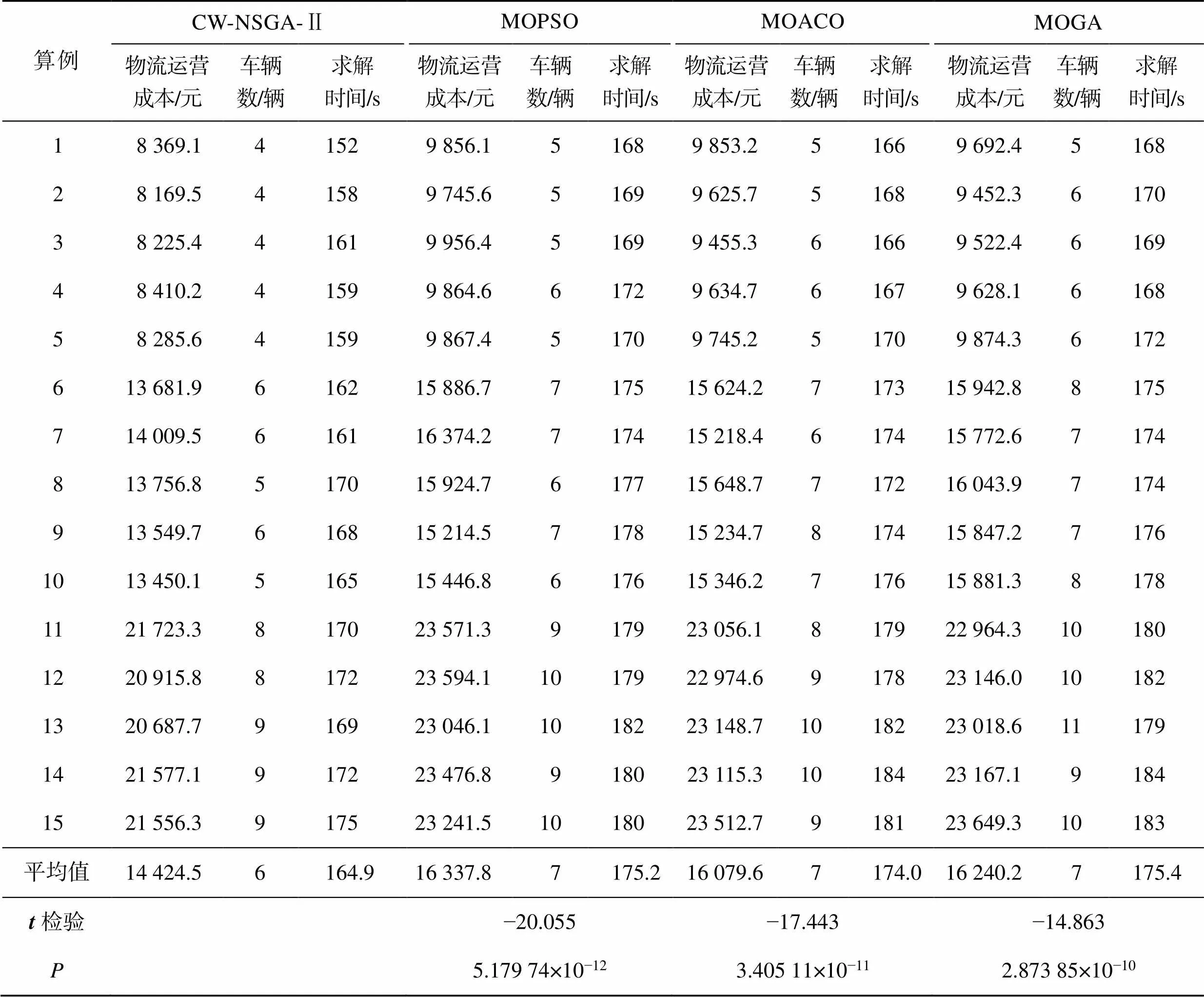
Tab.4 Comparison of optimization results of different algorithms

4 实例分析

4.1 相关数据

以重庆市某生鲜商品配送中心（D）所服务的100个客户点（1～100）为研究对象，配送中心与客户点的地理位置分布如图6所示。选取生鲜商品配送中心的部分商品类型，结合生鲜食品要求的温度分区，并考虑运输过程中的温控成本，将多仓配送车划分为3个车仓，并设置相应的温控区间，如配送樱桃、葡萄、玉米等蔬菜、水果的温控区间为1～5 ℃，鱼、虾等海鲜商品的温控区间为−5～0 ℃，冷冻水饺、冰激凌等冷冻商品的温控区间为−10～−6 ℃。具体信息如表5所示，相关参数设置[27-28]如表6所示。

图6 配送中心与客户的地理分布

表5 生鲜商品温控区间及商品种类

Tab.5 Temperature control ranges and product categories

4.2 优化结果及分析

针对基于时间窗和多仓温控的生鲜商品配送车辆路径优化问题，以最小化物流运营成本和多仓配送车辆使用数为目标，应用CW-NSGA-Ⅱ算法对模型进行求解。优化前后运营成本、多仓配送车使用数量及温控成本等指标变化情况如表7所示。

表6 参数设置

Tab.6 Parameter settings

由表7可知，优化后，配送车辆的使用数减少了5辆，运营成本减少了14 093.4元，温控成本减少了1 847.5元，惩罚成本减少了89.3%，配送距离缩减了49.0%。基于时间窗和多仓温控的生鲜商品配送车辆路径优化方案如表8和图7所示。

如图7a所示，在优化后配送车辆数减少了5辆，仅需要9辆多仓配送车为所有客户点提供服务。如图7b所示，9辆多仓配送车中有5辆处于满载状态，其余4辆多仓配送车的车仓剩余装载空间均小于18%，实现了车仓容量的合理利用。

4.3 分析与讨论

进一步探讨了不同车仓数目对各项运营指标的影响，分别研究了3种情形。结果如表9和图8所示。

1）多仓配送车有3个车仓，将车仓温度区间分别设置为1～5 ℃、−5～0 ℃、−10～−6 ℃。

2）相较于情形1，将多仓配送车增加1个1～5 ℃的车仓，共有4个车仓。

3）相较于情形2，将多仓配送车增加1个−5～0 ℃的车仓，共有5个车仓。

表7 基于时间窗和多仓温控的生鲜商品配送车辆路径优化结果前后对比

Tab.7 Comparison between fresh commodity distribution routes based on time windows and multi-compartment temperature control before and after the optimization

表8 优化后车辆配送方案

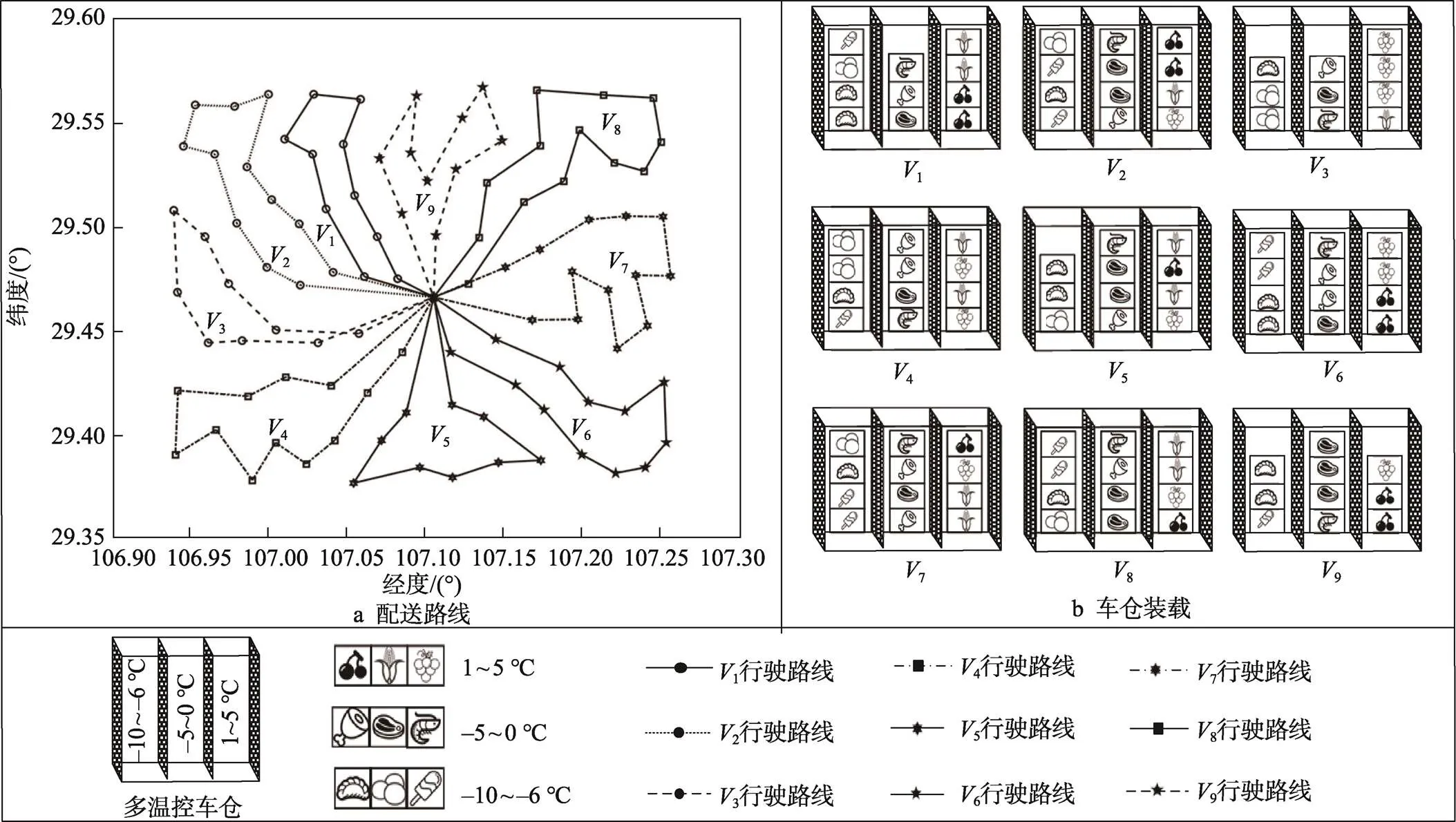
图7 配送路径

表9 不同车仓下的优化结果对比

Tab.9 Comparison of optimization results under different compartment numbers

图8 不同车仓下的各项指标结果对比

如表9和图8所示，以车仓外温度为20 ℃和3个车仓为研究基准，比较了不同车仓数量对各项运营指标的影响。当车仓数量增至4个时，多仓配送车的使用数量不变，而温控成本增加了984.9元，行驶成本增加了1 313.7元，运营成本增加了2 848.6元。当车仓数量增至5个时，多仓配送车的使用数量保持不变，而温控成本增加了1 394.1元，惩罚成本增加了1 200元，运营成本增加了3 800.3元。结果显示，在车仓外温度为20 ℃的情况下，当配送车辆具有3个车仓时，路径优化结果优于其他2种场景。

5 结语

研究了基于时间窗和多仓温控的生鲜商品配送车辆路径问题。首先，建立了最小化运营成本和多仓配送车使用数量的双目标优化模型。其次，设计了CW-NAGA-Ⅱ算法，以求解该模型，通过CW节约算法生成初始种群，并设计了精英迭代策略，以提高算法的寻优性能。最后，将CW-NAGA-Ⅱ算法与MOPSO、MOACO、MOGA进行比较分析，验证了CW-NAGA-Ⅱ算法的有效性。

以重庆某生鲜商品配送网络为例，对配送路径进行优化，提出了相应的优化方案。结果表明，优化后多仓配送车使用数量减少了35.7%，运营成本缩减了47.7%，温控成本从4 710.1元降至2 862.6元。此外，对比分析了不同车仓数量场景下的优化结果。结果显示，在生鲜商品需求量一定的情况下，选择合适车仓数目的多仓配送车可以有效降低运营成本和车辆使用数。文中研究为基于时间窗和多仓温控的生鲜商品配送车辆路径问题研究提供了新的切入点。

[1] 张文礼. 国务院办公厅印发《“十四五”冷链物流发展规划》[N]. 中国质量报, 2021-12-14(001).

ZHANG W L. Issued by The General Office of the State Council "14th Five-Year Plan" Cold Chain Logistics Development Plan[N]. China Quality Daily, 2021-12-14(001).

[2] CHRISTOFIDES N, MINGOZZI A, TOTH P. The Vehicle Routing Problem[J]. Revue Frangaise d'Informatique et de Recherche Opérationnelle, 1976, 10(2): 55-70.

[3] COELHO L C, LAPORTE G. Classification, Models and Exact Algorithms for Multi-Compartment Delivery Problems[J]. European Journal of Operational Research, 2015, 242(3): 854-864.

[4] 孙丽君, 周雅娴, 石海洋, 等. 多种横向转运配送方式下的成品油配送方案优化方法[J]. 系统管理学报, 2020, 29(6): 1177-1187.

SUN L J, ZHOU Y X, SHI H Y, et al. An Approach to Optimizing Distribution Plans of Oil Products for Multiple Distribution Schemes with Lateral Transshipment[J]. Journal of Systems & Management, 2020, 29(6): 1177-1187.

[5] CHEN L, LIU Y, LANGEVIN A. A Multi-Compartment Vehicle Routing Problem in Cold-Chain Distribution[J]. Computers & Operations Research, 2019, 111: 58-66.

[6] OSTERMEIER M, HÜBNER A. Vehicle Selection for a Multi-Compartment Vehicle Routing Problem[J]. European Journal of Operational Research, 2018, 269(2): 682-694.

[7] 王淑云, 孙虹, 牟进进. 随机需求下蓄冷式多温共配优化模型[J]. 系统管理学报, 2018, 27(4): 712-721.

WANG S Y, SUN H, MOU J J. Optimization of Cold-Storage Multi-Temperature Joint Distribution Based on Stochastic Demands[J]. Journal of Systems & Management, 2018, 27(4): 712-721.

[8] 李军涛, 刘明月, 刘朋飞. 生鲜农产品多车型冷链物流车辆路径优化[J]. 中国农业大学学报, 2021, 26(7): 115-123.

LI J T, LIU M Y, LIU P F. Route Optimization of Multi-Vehicle Cold Chain Logistics for Fresh Agricultural Products[J]. Journal of China Agricultural University, 2021, 26(7): 115-123.

[9] ZULVIA F E, KUO R J, NUGROHO D Y. A Many-Objective Gradient Evolution Algorithm for Solving a Green Vehicle Routing Problem with Time Windows and Time Dependency for Perishable Products[J]. Journal of Cleaner Production, 2020, 242: 118428.

[10] 梁桂云, 陈淮莉. 基于NSGA Ⅱ的生鲜品冷链配送联合调度优化[J]. 上海海事大学学报, 2022, 43(3): 28-35.

LIANG G Y, CHEN H L. Integrated Scheduling Optimization of Fresh Food Cold Chain Distribution Based on NSGA Ⅱ[J]. Journal of Shanghai Maritime University, 2022, 43(3): 28-35.

[11] LIU G K, HU J Y, YANG Y, et al. Vehicle Routing Problem in Cold Chain Logistics: A Joint Distribution Model with Carbon Trading Mechanisms[J]. Resources, Conservation and Recycling, 2020, 156: 104715.

[12] 杨森炎, 宁连举, 商攀. 基于时空状态网络的电动物流车辆路径优化方法[J]. 交通运输系统工程与信息, 2021, 21(2): 196-204.

YANG S Y, NING L J, SHANG P. Electric Logistics Vehicle Routing Optimization Based on Space-Time-State Network[J]. Journal of Transportation Systems Engineering and Information Technology, 2021, 21(2): 196-204.

[13] 李想, 闵德权, 张祺. 随机需求下半开放式冷链物流车辆路径优化[J]. 包装工程, 2022, 43(7): 160-169.

LI X, MIN D Q, ZHANG Q. Routing Optimization of Semi-Open Cold-Chain Logistics Vehicle under Random Demand[J]. Packaging Engineering, 2022, 43(7): 160-169.

[14] WANG Y, ZHANG J, ASSOGBA K, et al. Collaboration and Transportation Resource Sharing in Multiple Centers Vehicle Routing Optimization with Delivery and Pickup[J]. Knowledge-Based Systems, 2018, 160: 296-310.

[15] XIAO Y Y, ZHAO Q H, KAKU I, et al. Development of a Fuel Consumption Optimization Model for the Capacitated Vehicle Routing Problem[J]. Computers & Operations Research, 2012, 39(7): 1419-1431.

[16] 王思洪, 梁承姬, 张悦. 带温度决策与质量管理的冷链物流配送优化[J]. 制造业自动化, 2023, 45(4): 125-130.

WANG S H, LIANG C J, ZHANG Y. Optimization of Cold Chain Logistics Distribution with Temperature Decision and Quality Management[J]. Manufacturing Automation, 2023, 45(4): 125-130.

[17] 张异. 包装废弃物回收车辆路径问题的改进遗传算法[J]. 包装工程, 2018, 39(17): 147-152.

ZHANG Y. Improved Genetic Algorithm for Vehicle Routing Problem in Packaging Waste Recycling[J]. Packaging Engineering, 2018, 39(17): 147-152.

[18] 王勇, 罗思妤, 镇璐, 等. 考虑违约追偿和损失补偿的多中心集配网络联盟优化问题[J]. 中国管理科学, 2023, 31(3): 10-25.

WANG Y, LUO S Y, ZHEN L, et al. Multi-Center Pickup and Delivery Network Alliance Optimization Considering Default Penalties and Loss Compensations for Breach of Contract[J]. Chinese Journal of Management Science, 2023, 31(3): 10-25.

[19] 刘凡, 张惠珍, 周迅. 带模糊需求的开放式选址路径问题的混合离散蘑菇繁殖算法[J]. 计算机应用研究, 2021, 38(3): 738-744.

LIU F, ZHANG H Z, ZHOU X. Hybrid Discrete Mushroom Reproduction Algorithm for Solving Open Location-Routing Problem with Fuzzy Demands[J]. Application Research of Computers, 2021, 38(3): 738-744.

[20] İLHAN İ. An Improved Simulated Annealing Algorithm with Crossover Operator for Capacitated Vehicle Routing Problem[J]. Swarm and Evolutionary Computation, 2021, 64: 100911.

[21] SAĞ T. PVS: A New Population-Based Vortex Search Algorithm with Boosted Exploration Capability Using Polynomial Mutation[J]. Neural Computing and Applications, 2022, 34(20): 18211-18287.

[22] ASGHARI M, MIRZAPOUR AL-E-HASHEM S M J. A Green Delivery-Pickup Problem for Home Hemodialysis Machines; Sharing Economy in Distributing Scarce Resources[J]. Transportation Research Part E: Logistics and Transportation Review, 2020, 134: 101815.

[23] HAN H G, ZHANG L L, HOU Y, et al. Adaptive Candidate Estimation-Assisted Multi-Objective Particle Swarm Optimization[J]. Science China Technological Sciences, 2022, 65(8): 1685-1699.

[24] 赵志学, 李夏苗, 周鲜成, 等. 考虑交通拥堵的冷链物流城市配送的GVRP研究[J]. 计算机工程与应用, 2020, 56(1): 224-231.

ZHAO Z X, LI X M, ZHOU X C, et al. Research on Green Vehicle Routing Problem of Cold Chain Distribution: Considering Traffic Congestion[J]. Computer Engineering and Applications, 2020, 56(1): 224-231.

[25] PIERRE D M, ZAKARIA N. Stochastic Partially Optimized Cyclic Shift Crossover for Multi-Objective Genetic Algorithms for the Vehicle Routing Problem with Time-Windows[J]. Applied Soft Computing, 2017, 52: 863-876.

[26] 文展, 唐康健, 李文藻. 一种改进粒子群优化算法在车辆路径问题的应用研究[J]. 重庆邮电大学学报(自然科学版), 2020, 32(5): 891-897.

WEN Z, TANG K J, LI W Z. Research on Application of Vehicle Routing Problem Using an Enhanced Particle Swarm Optimization[J]. Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition), 2020, 32(5): 891-897.

[27] 范厚明, 吴嘉鑫, 耿静, 等. 模糊需求与时间窗的车辆路径问题及混合遗传算法求解[J]. 系统管理学报, 2020, 29(1): 107-118.

FAN H M, WU J X, GENG J, et al. Hybrid Genetic Algorithm for Solving Fuzzy Demand and Time Windows Vehicle Routing Problem[J]. Journal of Systems & Management, 2020, 29(1): 107-118.

[28] 方文婷, 艾时钟, 王晴, 等. 基于混合蚁群算法的冷链物流配送路径优化研究[J]. 中国管理科学, 2019, 27(11): 107-115.

FANG W T, AI S Z, WANG Q, et al. Research on Cold Chain Logistics Distribution Path Optimization Based on Hybrid Ant Colony Algorithm[J]. Chinese Journal of Management Science, 2019, 27(11): 107-115.

Fresh Commodity Distribution Vehicle Routing Optimization Based on Time Windows and Multi-compartment Temperature Control

WANG Yong, WANG Jingyuan,GOU Mengyuan,LUO Siyu

(Chongqing Jiaotong University, Chongqing 400074, China)

Aiming at the inefficient and high-cost fresh commodity distribution, the work aims to study the fresh commodity distribution route optimization based on time windows and multi-compartment temperature control by adopting multi-compartment vehicles with temperature controlled compartments as distribution equipment and applying time windows and other constraints. Firstly, the bi-objective model was established to minimize logistics operating cost and the number of vehicles. Then, the non-dominated sorting genetic algorithm based on the Clarke-Wright saving algorithm (CW-NSGA-Ⅱ) was designed to solve the model. Among them, the initial population was generated by the Clarke-Wright saving algorithm, which improved the quality of the initial solution, and an elite iterative strategy was designed to improve the optimization performance.Based on the improved Solomon example, the proposed algorithm was compared with the multi-objective particle swarm algorithm, multi-target ant colony algorithm and multi-target genetic algorithm, verifying the solution performance of the CW-NSGA-Ⅱ. Combined with a case study, the indicators such as the number of multi-compartment vehicles, temperature control costs and operating costs were compared and analyzed. The results showed that the number of optimized multi-compartment vehicles was reduced by 35.7%, the temperature control cost was reduced by 39.2%, and the total operating cost was reduced by 47.7%. The proposed model and algorithm can effectively optimize the distribution route, reduce the total operating cost, and provide theoretical support and decision-making reference for the construction of the efficient and low-cost fresh distribution network.

fresh commodity distribution; multi-compartment temperature control; time window; CW-NSGA-Ⅱ

F570；TB485.3

A

1001-3563(2024)05-0263-13

10.19554/j.cnki.1001-3563.2024.05.032

2023-09-28

国家自然科学基金（72371044，71871035）；重庆市教委科学技术研究重大项目(KJZD-M202300704)；重庆市自然科学基金面上项目（CSTB2022NSCQ-MSX0535）；巴渝学者青年项目（YS2021058）