基于遗传粒子群动态聚类算法的物流柔性分拣系统品规分配
杜佳奇,杨旭东*,孙栋,张磊,王晋冰
基于遗传粒子群动态聚类算法的物流柔性分拣系统品规分配
杜佳奇1,杨旭东1*,孙栋2,张磊3,王晋冰3
(1.贵州大学 机械工程学院,贵阳 550000;2.贵州理工学院,贵阳 550000; 3.贵州省烟草公司贵阳市公司,贵阳 550000)
针对目前烟草物流配送中心条烟分拣量大,不同条烟品规的分配对订单的总处理时间影响较大的问题,研究平衡各个分拣区品规的分配,提高分拣效率。建立以各分区品规相似系数和最小为目标函数的数学模型,并采用改进的遗传粒子群动态聚类(GAPSO-)算法进行求解。首先,结合各品规分拣量对品规相似系数进行改进,并将其作为适应度函数;然后在粒子群算法中对惯性权重因子进行改进,使其值可以进行自适应改变;最后,在粒子群动态聚类算法中引入遗传算法中的交叉变异扩大解的搜索范围,基于Matlab对文中的其他算法进行求解对比,求得结果在EM-plant中进行仿真验证。结合某烟草物流配送中心数据仿真验证,利用GAPSO-算法处理订单的时间为234.5 s,较传统时间大幅度较少,有效提升了柔性物流分拣效率。采用该算法可充分发挥2种算法的优良性,具有更好的收敛性及寻优性,为柔性物流品规分配提供了新思路。
品规分配;品规相似系数;惯性权重因子;遗传粒子群动态聚类算法
由于自动化程度差异,物流分拣可被分为人工分拣(MSS)和自动化分拣系统(ASS)[1]。自动化分拣具有效率高、出错率低、常被用于柔性分拣中。柔性分拣由于嵌入了信息化、模块化、可视化、机械化、电子化等组件,故而其分拣过程中可以通过上位机及时进行信息反馈,并对分拣过程中出现的问题及时反馈。物流柔性分拣策略为多个分区对同一订单中的烟并行分拣,并暂时存储至缓存区,等待上一分区流过后缓存区挡板上下开合进行有序合流。并行分拣下,订单总处理时间由各个分拣区中分拣时间最长的分拣时间决定,各个分拣区的分拣时间是由订单在该分区分拣的各品规的分拣量决定,若将2个分拣量较大的品规放在一个分拣区进行分拣将延长该分区的分拣时间,从而影响订单的总处理时间。基于此本文将减少订单总处理时间作为目标来对分区之间的品规分配问题进行研究。
张贻弓等[2]对自动分拣系统的品规分配优化提出了最大最小蚁群算法(MMAS)结合动态优化来求解模型。刘靖明等[3]针对-均值聚类算法易陷入局部收敛结合了粒子群算法,来对聚类问题进行更好效果的求解。李建明等[4]在品项似系数中加入了分拣量的影响因子,并采用了结合禁忌搜索算法的动态聚类对品项分配模型进行求解。王艳艳等[5]分析了品规的分拣量拆分对并行分拣系统延时时间的影响,并设计启发式算法进行求解。Lee等[6]对基于品规之间的关联性差异分配货位问题,提出了一种启发式聚类算法进行求解,再结合关联性差异和空间填充曲线来对货位区域进行分配。Peterson等[7]在人工分拣系统里,分析品规分配影响的因素,得到人在分拣区行走距离受品规分配的影响较大。Wu等[8]针对品规分配聚类问题,建立了0-1整数规划模型,利用订单的总数和各个品规订购量确定品规相似系数,采用归类方法进行求解。Garfinkel等[9]考虑到入库时货物品规间的相似性,采用循环交换算法进行求解分析。Liu等[10]根据订单、品规数、分拣量3个限制条件分别对品规和客户定义2个变量进行对比,建立了0-1整数规划模型,提出原始-对偶算法求解模型。本文考虑到粒子群结合动态聚类算法在解的搜索过程中容易陷入局部最优,故在粒子群算法的基础上结合遗传算法中的交叉变异来扩大解的搜索范围,提高收敛速度。
在现有的品规分配问题中,有着较多启发式算法来求解问题,如:遗传算法、粒子群算法、灰狼算法等。但这类算法对解搜索过程中依赖于参数的设定,存在陷入局部最优的死角。故以上算法各自都有其适用的途径,并不具备解决多种问题的普遍性,需要在已有的算法中进行组合优化。基于此,本文对如何均衡分拣区之间的品规分配问题进行研究,建立以各分区品规相似系数之和为适应度函数的数学模型,并提出2种聚类算法求解模型;然后针对动态聚类算法中的均值取聚类中心容易陷入局部最优的缺点,利用粒子群算法中的种群寻优和遗传算法中的交叉、变异等步骤对动态聚类算法进行改进;最后经过某烟草物流中心实例仿真验证该改进算法的高效性。
1 问题描述
1.1 物流柔性分拣系统
物流柔性分拣系统主要由立式机、卧室机、开箱机、滑箱机、传输皮带等部分组成,目前大部分物流柔性分拣线采取异型烟和标准烟混合分拣的方式,由于异型烟具有尺寸不同、分拣量较少、品规数量多等特点,故而异型烟进行自动化分拣难度较大,对自动分拣系统设计有着较高要求。本文对某烟草物流分拣中心进行现场场景建模,如图1所示。整个分拣系统由4条分拣线组成,分别为3条复合一体化分拣线以及1条异型烟分拣线,提高了异型烟分拣及标烟分拣效率。

图1 烟草物流分拣中心
物流柔性分拣系统有2种分拣方式:串行分拣、并行分拣[11]。串行分拣策略:前一个分拣区对订单分拣完成后,后一个分拣区可进行分拣,该分拣策略适合分拣小批量小品规物品。并行分拣策略:多个分拣区对一个订单同时分拣,依次进行合流,该分拣策略适合大批量多品规的物流柔性分拣系统[12]。由于分拣机中的卧式机品规种类较少,而立式机的品规种类较多,故本文主要研究内容为立式机的品规分配。对一定数量的立式机进行分区,基于每个分区来对烟的品规进行分配,本文采取并行分拣策略来进行分拣,如图2所示。本文研究方向为将烟的品规进行合理分配,提高分拣效率,减少订单总处理时间。

图2 并行分区柔性分拣系统
1.2 确定分区间的品规相似系数并改进
各订单在各分拣区的分拣时间越短,其分拣效率越高,订单的总处理时间就越短。为了减少各订单在各分拣区的分拣时间,条烟品规分配的均匀性较为重要。条烟的品规分配是将每个品种的烟指定到某个分拣机的分拣通道进行分拣,该问题可归结为分类已知数,是一个聚类问题。
Jane等[13]在聚类问题中引入了品规相似系数,用来表示2种品规在一个分区的共存关系。如式(1)所示,品规相似系数越大,表示该2种品规应该分配到不同的分拣区。
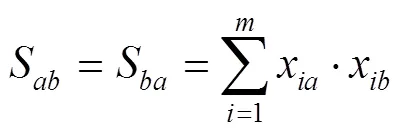

式中:S为品规与品规之间的品规相似系数;为待分拣订单的总数。式(2)为0-1变量,表示品规相似系数对应的2种品规必须同时出现在一个订单中。
由于在条烟物流分拣中,立式机每个储烟通道出烟时间相同,故分拣量也是制约分拣时间的关键因素。由于文献[13]提出来的品规相似系数并未考虑到条烟的分拣量,所以本文在品规相似系数中加入条烟的分拣量影响因子。考虑到品规分拣量可能会出现2种品规相同情况,为了避免无穷大产生,故而对分拣量影响因子添加条件数,如式(3)所示。
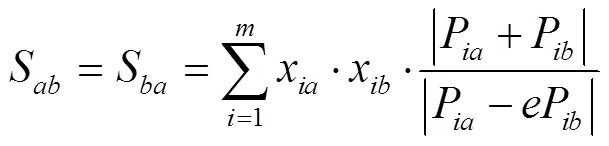
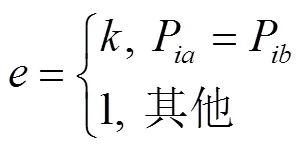
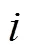
由式(3)可知,若两品规分拣量都十分大并且2种分拣量相差很大,品规相似系数就会较大,则2种品规应分到不同的分拣区;若2种品规分拣量都很小并且2种分拣量相差很小,则2种品规应分到一个分拣区进行分拣。
1.3 模型假设
为了建立更好的数学模型,做出如下假设:
1)前一个订单分拣完成后才可进行下一个订单的分拣。
2)各个分区的立式机完全相同,每台立式机每分拣一条烟所需的时间都相等。
3)立式机内的烟一直都余量充足,即补货效率高。
4)每种品规只能分配到一个立式机的一个分拣位。
2 品规分配优化建模
为了减少订单总处理时间,解决品规分配的聚类问题尤为重要。各分区品规相似系数和累加值越大,品规的分配越不均匀,订单的总处理时间越长。即订单总处理时间和各分区品规相似系数和累加值成正比,故将求订单总处理时间最小值转换为求各分区品规相似系数和累加值的最小值。目标函数如式(5)所示。
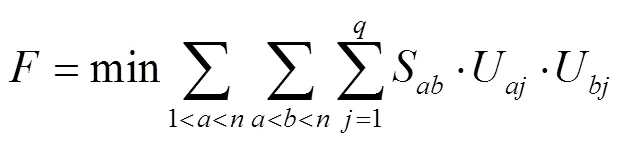
约束条件:
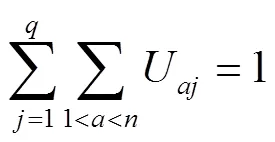

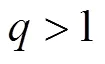
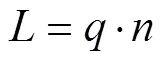
3 品规分配模型求解
3.1 动态聚类算法的设计
通过动态聚类算法(-means)求解品规分配问题模型,得到聚类中心。将各个品规的卷烟进行合理归类,归类后筛选最优解。算法流程如图3所示,求解品规分配问题步骤如下:
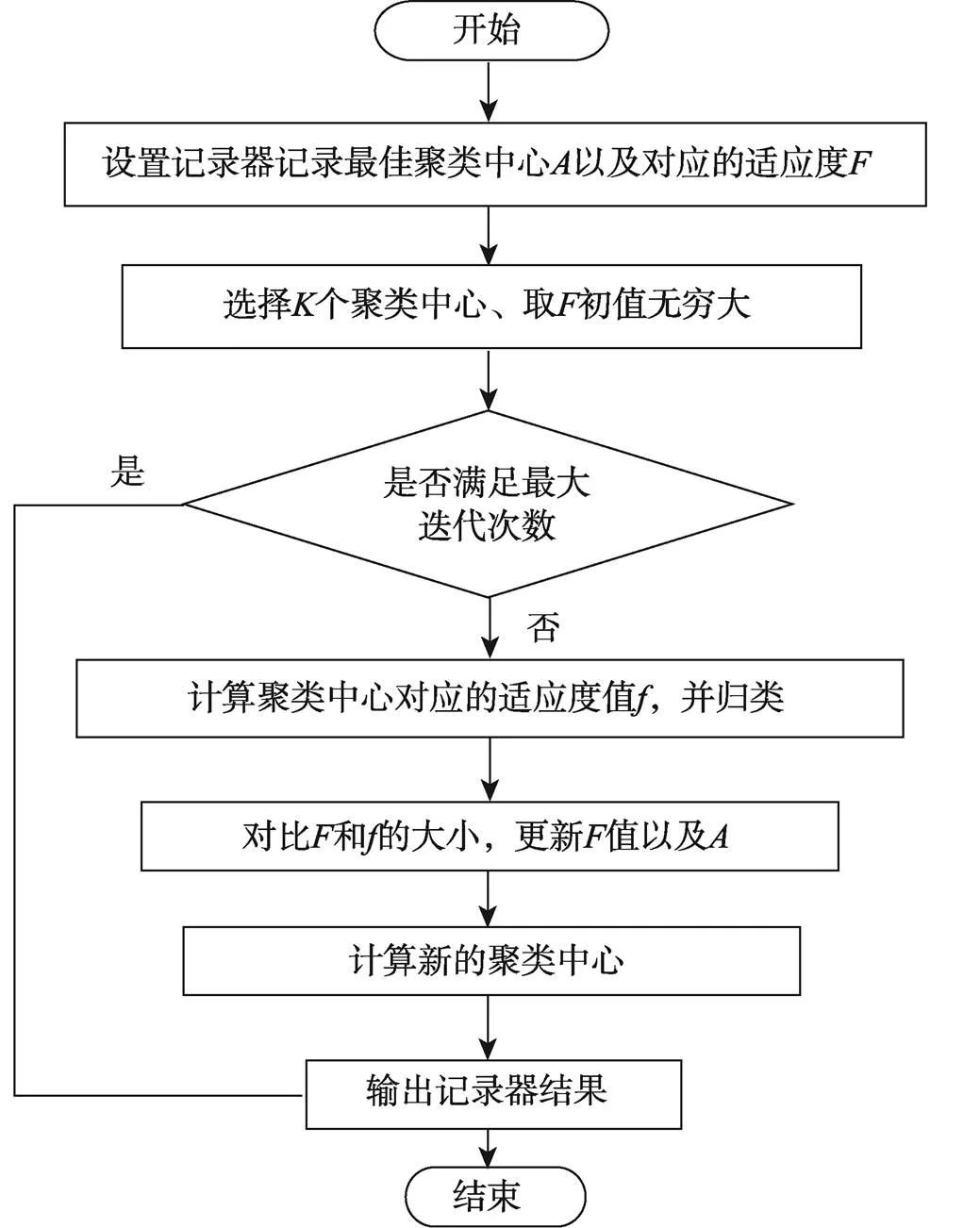
图3 K-means算法流程
1)随机选取个聚类中心。
2)用式(3)代替动态聚类算法中的欧氏距离判别,计算其余的每个品规和这个品规的品规相似系数,储存至行列的矩阵中。
3)寻找矩阵中每一行的最小值对应的分拣区号,记录每一个分拣区的个数为行1列的矩阵。设定每个分拣区最大容纳品规数为,先将中小于的品规进行分配,后将中大于的品规进行分配,按照从小到大品规相似系数对分拣区进行品规分配,将分配完的品规从矩阵中删除。
4)计算未全部完成分配品规的各个分拣区品规相似系数之和(),取其中最小值对应的分拣区,从矩阵中找出对应该分拣区品规相似系数的最小值。将最小值对应的品规分配至该分拣区。
5)判断是否存在未完成分配的分拣区,若存在则转步骤4,若不存在则转步骤6。
6)求新的聚类中心,即求每个分区的所有品规数的均值然后取整。
7)判断聚类中心是否已经不变,或者已经达到最大迭代次数;若没有则转步骤2。
由求解步骤可知,该算法可以快速地求得较好的聚类结果,但是以最小()为聚类标准限制了搜寻解的范围。一旦有一两个坏点的产生,进行后续迭代容易会让算法陷入局部收敛。
3.2 GAPSO-K算法设计
3.2.1 适应度函数

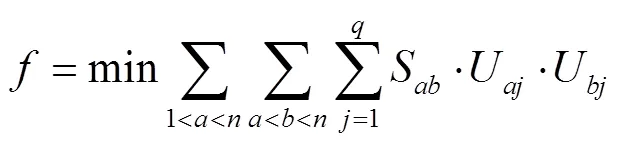
3.2.2 粒子信息更新
粒子特征信息有速度和位置,按照式(12)和式(13)对种群中的每个粒子进行速度和位置的更新。
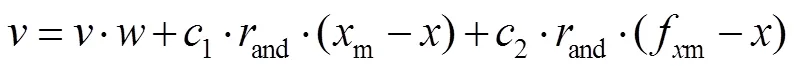

3.2.3 选择
根据个体的适应度大小不同进行选择。选择方法常用的有轮盘赌、精英选择等。精英选择操作步骤是先选取适应度前/2个个体,然后进行后续的交叉变异等操作,但精英选择容易让搜寻解陷入到局部最优。轮盘赌则是按照适应度的不同来计算每一个粒子被选中的概率。其中遵循适应度越大个体越容易被选中,扩大了对下一代个体的搜索范围,不易陷入局部最优[14]。轮盘赌示意图如图4所示,本文采取轮盘赌的选择方式来对粒子进行选择,粒子被选中的概率为:
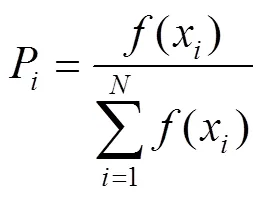
式中:为粒子i的适应度。
3.2.4 交叉
采取基于交叉因子[15]的方式进行两两交叉。将轮盘赌选择出来的2个父代粒子进行交叉得到子代粒子,对比子代父代适应度大小,选择最优粒子进入下一代,其余没有被选择的粒子直接进入下一代。这样通过交叉不但可以增加粒子的多样性,不容易让求解过程陷入局部最优解,而且可以加快求解速度,减少迭代次数。子代粒子的位置以及速度计算方法如式(15)~(16)所示。

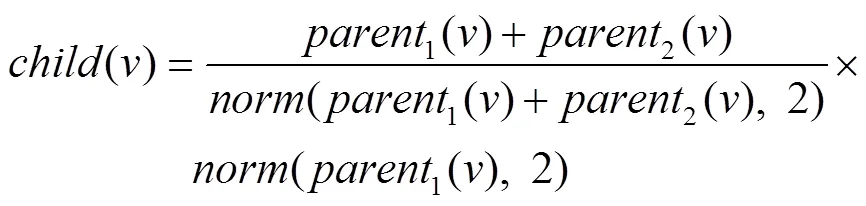
3.2.5 变异

3.2.6 惯性权重因子改进
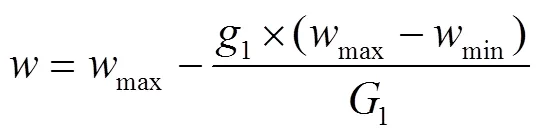
3.2.7 速度位置限制
因粒子群算法在搜索最优解过程中容易出现速度或者位置超过设定的范围,故要加以限制让解的范围得到约束。
3.3 遗传粒子群动态聚类(GAPSO-K)算法求解
遗传算法(GA)是模拟自然界物竞天择、适者生存的定律而产生的一种自适应全局优化算法,其基本步骤为编码、选择、交叉、变异等。通过逐代筛选,直到算法达到最大迭代次数结束。粒子群算法(PSO)是模仿自然界中鸟类的群体捕食行为,将每个个体称为粒子,用位置、速度、适应度来表征。粒子利用自身历史最佳位置和种群历史最佳位置来更新速度和位置,信息更新完计算适应度来衡量优劣程度[16]。
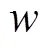

图5 GAPSO-K算法流程

7)若迭代次数超过最大迭代次数或者种群的最佳位置不发生变化则算法结束,否则转到步骤3。
4 仿真分析
4.1 仿真数据
为了验证该算法性能,本文利用MATLAB通过仿真方法对GAPSO-、粒子群动态聚类(PSO-)、-means等3种算法进行了对比分析。参数设置如下:各个立式机分拣通道分拣一件烟的时间=0.3 s,每个缓存区的合流时间=1 s,品规总数=50,订单的总数=10。每个订单中的每种品规分拣量如表1所示。
表1 各品规在各订单中的分拣量
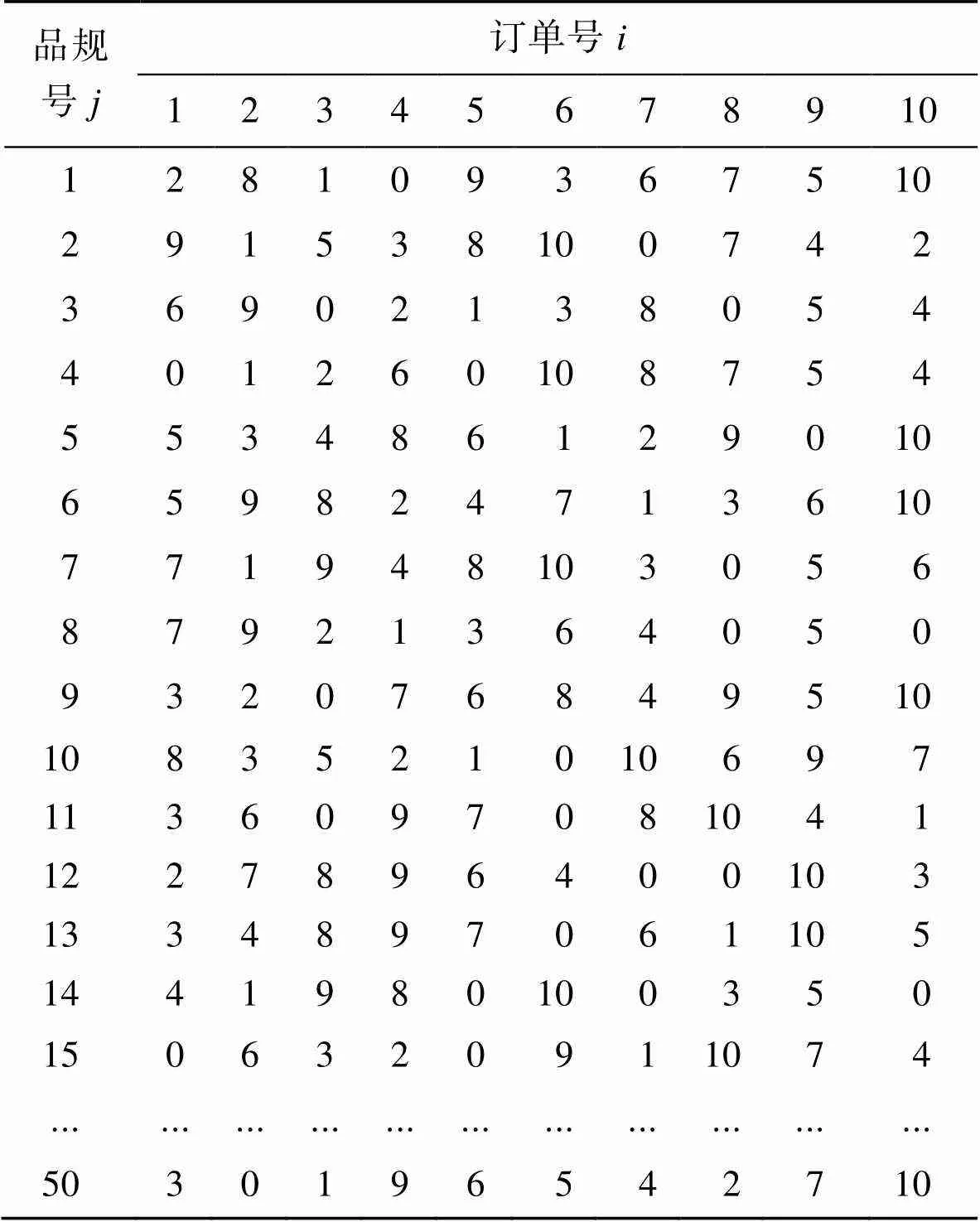
Tab.1 Picking volume for each specification in each order
4.2 仿真结果与分析
对3种优化算法(GAPSO-、PSO-和-means)在MATLAB上进行30次仿真验证,其算法的初始参数设定如表2所示。仿真结果最优值结果见表3。
表2 GAPSO-参数
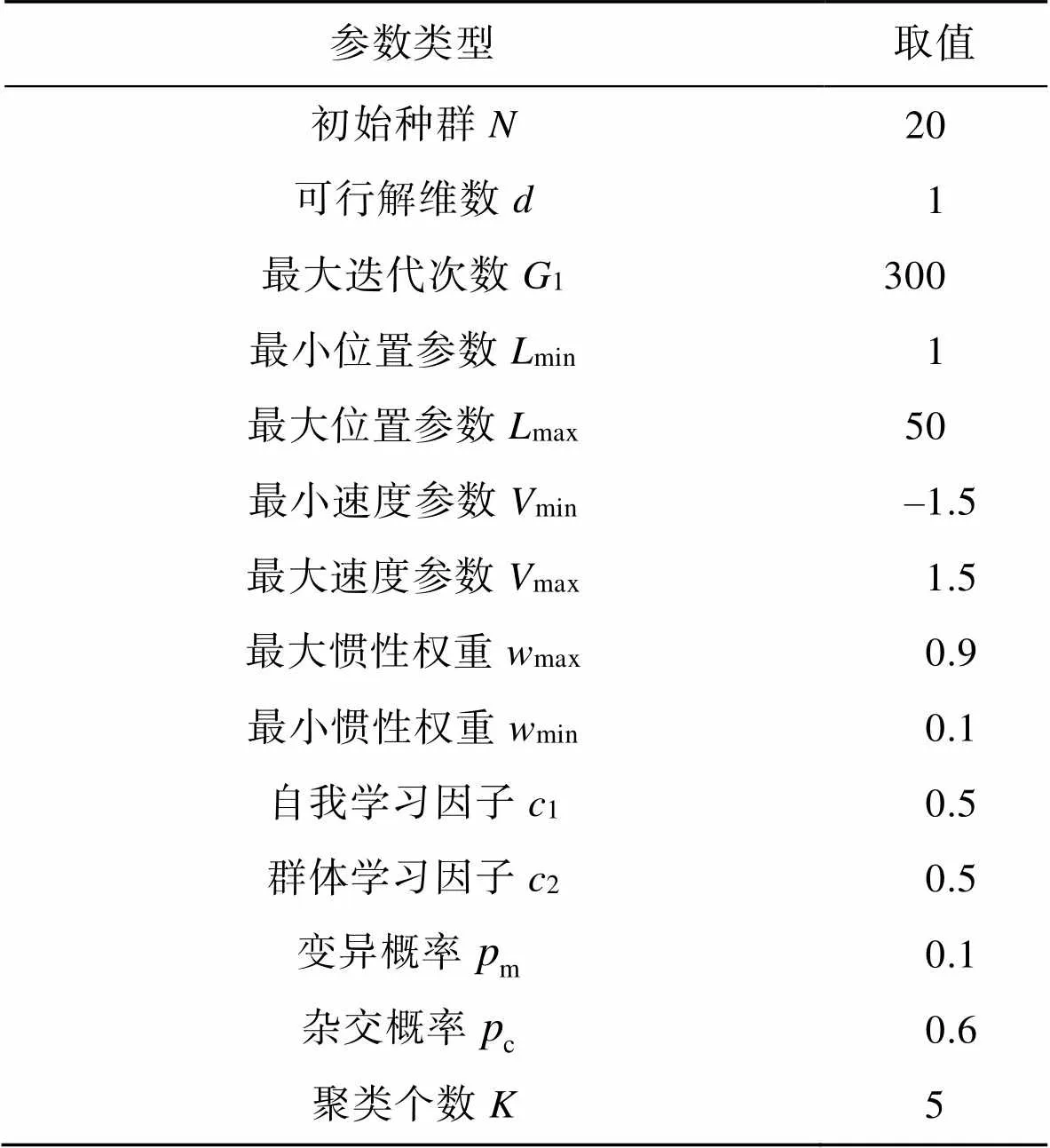
Tab.2 GAPSO-K parameters
表3 优化后的品规号分配

Tab.3 Optimized specification number allocation
利用EM-Plant软件对分拣系统工艺流程图进行1∶1建模,并按照实际运行时需要的各种参数赋予模型中的各个设备。按照分拣系统实际统运行时的控制方法,编写该仿真系统的各种控制策略。将3种算法得出的品规分配优结果利用EM-Plant软件进行仿真验证,其复合一体化分拣系统二维模型如图6所示。其系统是由补货小车、卧式机、立式机、传输带、缓存区、包装机等部分构成。在EM-Plant中设置与实际物流系统相近的参数,达到与实际高度相关,故可在EM-Plant进行模拟得到较好的品规分配方案,从而减少订单总处理时间。
现场布局由3条复合一体化分拣线以及一条异型烟分拣线组成。本文主要研究立式机的品规分配对订单总处理时间的影响,故取其中的异型烟分拣线进行研究。其中每个分拣区代表异型烟分拣线的一个子线,异型烟分拣线如图7所示。现场采用了5条异型烟子线,故而本文讨论的分区数目也为5,整个异型烟分拣线模型由立式机、传输带、缓冲区、合单区、包装机等部分组成。由于现场布局条件使得每个子线传输带长度不同,在EM-Plant中模拟传输带的长度来表示。
对前文经过3种算法得出的品规分配结果在异型烟分拣线中进行仿真模拟获取订单总处理时间,并且将各个分拣区的品规相似系数和累加值、订单的总处理时间进行对比,如表4所示。
由表4可知,对比3种算法优化后得到的平均值,PSO-算法相较于-means算法提升了10.2%,GAPSO-算法相较于-means算法提升了15.2%。对比优化后的平均值,PSO-算法相较于-means算法提升了12.5%,GAPSO-算法相较于-means算法提升了16.4%。由于GAPSO-算法是在PSO-算法基础上进行改进的,2种优化算法具有一定的相似性,相较于PSO-算法只提升了5.6%。因此按照GAPSO-算法得到的品规分配结果最好,能大幅度降低订单总处理时间,提高分拣效率。
对比MATLAB仿真结果中3种算法最优值对品规相似系数和的进化过程如图8所示。

图6 复合一体化分拣系统二维模型
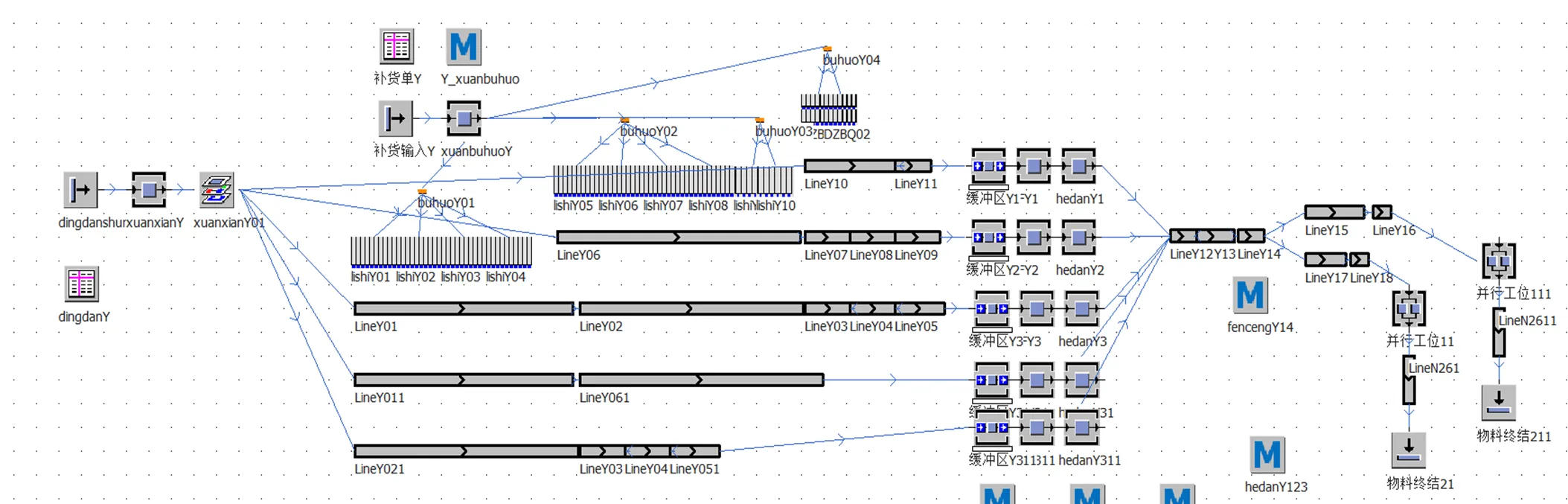
图7 异型烟分拣线模型
表4 仿真结果对比

Tab.4 Comparison of simulation results
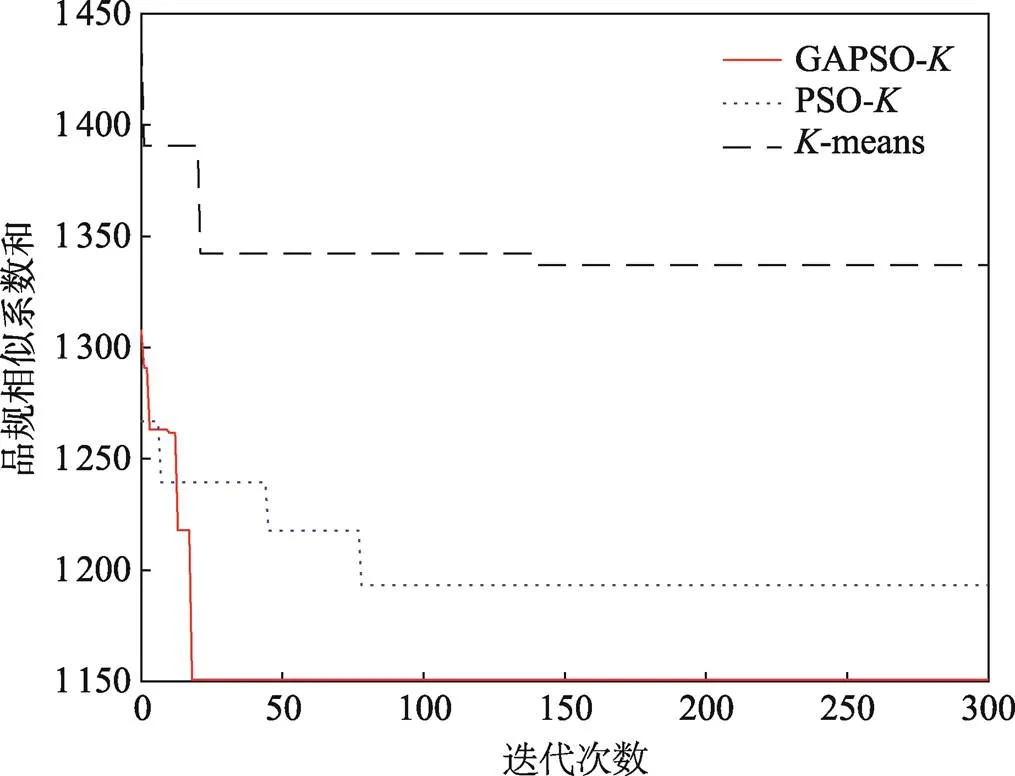
图8 3种算法最优适应度进化过程对比
GAPSO-在迭代了18次后完成收敛,为1 150;PSO-在迭代78次后收敛于1 193,-means则于139次迭代后收敛于1 337。GAPSO-有最少的迭代次数和最优的收敛结果,效果明显优于其他2种算法,并且经过EM-Plant软件的验证得出该算法处理后的品规对订单的总处理时间明显低于其他2种算法。
5 结语
本文针对柔性物流分拣系统,以品规相似系数作为适应度函数建立品规聚类模型,针对模型求解提出一种具有创新性的改进遗传粒子群动态聚类算法。考虑到品规分拣量对适应度函数的影响,对品规项系数引入了分拣量以及条件数进行改进。为提高算法子代选择多样性,在算法中添加了遗传操作中的交叉变异来提高搜索范围。利用MATLAB进行算法求解,通过算例对比,证明所提算法对品规分配问题具有较好的适应性。结合某烟草物流实例数据,利用EM-Plant软件进行系统仿真,相比其他2种算法,采用GAPSO-算法得到的订单总处理时间从302.4 s减少至252.7 s,订单总处理时间较-means算法的减少了16.4%,相较PSO-算法减少了5.6%,分拣效率明显提升。结果表明了本文提出的GAPSO-算法适用于物流柔性分拣系统的品规分配,为提高物流柔性分拣系统的效率提供了新思路。
本文仅考虑了立式机的品规分配对订单总处理时间的影响,但是在柔性物流分拣中卧式机品规分配对分拣效率的影响也是不可忽略,因此卧式机品规分配问题有待进一步研究。
[1] DE KOSTER R B M, LE DUC T, ROODBERGEN K J. Design and Control of Warehouse Order Picking: A Literature Review[J]. European Journal of Operational Research, 2007(2): 481-501.
[2] 张贻弓, 吴耀华, 耿耀华. 并行拣选策略下的自动拣选系统品项分配优化[J]. 计算机工程与应用, 2011, 47(3): 240-243.
ZHANG Y G, WU Y H, GENG Y H. Item Assignment Optimization of Automated Picking System Based on Synchronized Zoning Strategy[J]. Computer Engineering and Applications, 2011, 47(3): 240-243.
[3] 刘靖明, 韩丽川, 侯立文. 基于粒子群的K均值聚类算法[J]. 系统工程理论与实践, 2005, 25(6): 54-58.
LIU J M, HAN L C, HOU L W. Cluster Analysis Based on Particle Swarm Optimization Algorithm[J]. Systems Engineering-Theory & Practice, 2005, 25(6): 54-58.
[4] 李建明. 物流配送中心分区自动分拣系统品项分配方法研究[D]. 兰州: 兰州交通大学, 2017: 16-31.
LI J M. Research on Item Distribution Method of Automatic Sorting System in Logistics Distribution Center[D]. Lanzhou: Lanzhou Jiatong University, 2017: 16-31.
[5] 王艳艳, 吴耀华, 吴颖颖. 并行自动拣选系统品项拣选量拆分优化[J]. 机械工程学报, 2013, 49(16): 177-184.
WANG Y Y, WU Y H, WU Y Y. SKU Picking Quantity Splitting Optimization of Parallel Automatic Picking System[J]. Journal of Mechanical Engineering, 2013, 49(16): 177-184.
[6] LEE M K. A storage assignment policy in a man-on-board automated storage/retrieval system[J]. International Journal of Production Research, 1992, 30(10): 2281-2292.
[7] PETERSON C G, GERALD A. Considerations in Order Picking Zone Configuration[J]. International Journal of Operations & Production Management, 2002, 27: 793-805.
[8] WU C. An Association-Based Clustering Approach to Order Batching Considering Customer Demand Patterns[J]. Omega, 2005, 33(4): 333-343.
[9] GARFINKEL M. Minimizing Multi-Zone Orders in the Correlated Storage Assignment Problem[D]. Georgia: Georgia Institute of Technology, 2005.
[10] LIU C M. Clustering Techniques for Stock Location and Order-Picking in a Distribution Center[J]. Computers & Operations Research, 1999, 26(10/11): 989-1002.
[11] 杨姣. 烟草异标合一多模式分拣系统仿真研究[D]. 贵阳: 贵州大学, 2022: 37-49.
YANG J. Simulation Study of Tobacco Heterogeneous Multi-Mode Sorting System[D]. Guiyang: Guizhou University, 2022: 37-49.
[12] 李露莎. 多子线复杂烟草分拣系统研究[D]. 贵阳: 贵州大学, 2022: 22-42.
LI L S. Research on Multi-Subline Complex Tobacco Sorting System[D]. Guiyang: Guizhou University, 2022: 22-42.
[13] JANE C C, LAIH Y W. A Clustering Algorithm for Item Assignment in a Synchronized Zone Order Picking System[J]. European Journal of Operational Research, 2005, 166(2): 489-496.
[14] 张长勇, 刘佳瑜. 基于改进遗传算法的航空集装箱装载优化[J]. 包装工程, 2022, 43(11): 253-260.
ZHANG C Y, LIU J Y. Optimization of Aviation Container Loading Based on Improved Genetic Algorithm[J]. Packaging Engineering, 2022, 43(11): 253-260.
[15] 许晨, 康雪, 杨玲. 基于粒子群K均值聚类算法的多时相去云处理[J]. 成都信息工程大学学报, 2020, 35(4): 424-429.
XU C, KANG X, YANG L. Multi-Temporal Cloud Removal Based on Particle Swarm K-Means Clustering Algorithm[J]. Journal of Chengdu University of Information Technology, 2020, 35(4): 424-429.
[16] 吴延凯, 张伟, 王亚刚. 基于GA-PSO的印版滚筒温度二自由度PID参数整定[J]. 包装工程, 2020, 41(5): 185-191.
WU Y K, ZHANG W, WANG Y G. Parameter Tuning of Two-Degree-of-Freedom PID Controller for Plate Cylinder Temperature Based on GA-PSO[J]. Packaging Engineering, 2020, 41(5): 185-191.
Genetic Particle Swarm-based Dynamic Clustering Algorithm for Logistics Flexibility Sorting System of Specification Allocation
DU Jiaqi1, YANG Xudong1*, SUN Dong2, ZHANG Lei3, WANG Jinbing3
(1. School of Mechanical Engineering, Guizhou University, Guiyang 550000, China; 2. Guizhou University of Technology, Guiyang 550000, China; 3. Guiyang Branch of Guizhou Province Tobacco Company, Guiyang 550000, China)
In order to solve the problems of the large sorting quantity of cigarette in tobacco logistics distribution center and the great impact of assignment of cigarette specification on the total processing time of orders, the work aims to study the allocation of each sorting zone and improve the sorting efficiency. A mathematical model with the objective function of minimizing the similarity coefficients of specification in each zone was developed and solved by an improved genetic particle swarm dynamic clustering (GAPSO-) algorithm. Firstly, the similarity coefficient of each specification was improved by combining the sorting quantity of each specification as the fitness function. Then, the inertia weight factor was improved in the particle swarm algorithm so that its value could be changed adaptively. Finally, the cross-variance in the genetic algorithm was introduced in the particle swarm dynamic clustering algorithm to expand the search range of the solution, and the results were compared with the other algorithms based on Matlab. The results were simulated and verified in EM-plant. Combined with the data simulation verification in a tobacco logistics distribution center, the time for processing order with GAPSO-algorithm was 234.5 s, which was significantly reduced compared with the traditional time, effectively improving the efficiency of flexible logistics sorting. The use of this algorithm can give full play to the goodness of both algorithms, with better convergence and merit-seeking, and provides a new idea for flexible logistics product rule allocation.
product specification distribution; similarity coefficient of specifications; inertia weight factor; genetic particle swarm dynamic clustering algorithm
TB485.3;TP278
A
1001-3563(2024)05-0126-09
10.19554/j.cnki.1001-3563.2024.05.015
2023-09-20
贵州省烟草公司贵阳市公司科技项目(黔烟筑科(2022)1号);贵州省普通高等学校青年科技人才成长项目(黔教合KY字[2021]268)

