带有射频偏压源的感性耦合Ar/O2/Cl2等离子体放电的混合模拟研究*

佟磊 赵明亮 张钰如 宋远红 王友年

(大连理工大学物理学院,三束材料改性教育部重点实验室,大连 116024)

在刻蚀工艺中,通常会在感性耦合等离子体源的下极板上施加偏压源,以实现对离子能量和离子通量的独立调控.本文采用整体模型双向耦合一维流体鞘层模型,在Ar/O2/Cl2 放电中,研究了偏压幅值和频率对等离子体特性及离子能量角度分布的影响.研究结果表明: 当偏压频率为2.26 MHz时,随着偏压的增加,除了Cl–离子和ClO+离子的密度先增加后降低最后再增加外,其余带电粒子、O 原子和Cl 原子的密度都是先增加后基本保持不变最后再增加.当偏压频率为13.56 和27.12 MHz时,除了Cl–离子和 离子外,其余粒子密度随偏压的演化趋势与低频结果相似.随着偏压频率的提高,在低偏压范围内(<200 V),由于偏压源对等离子体加热显著增加,导致了带电粒子、O 原子和Cl 原子的密度增加;而在高偏压范围内(>300 V),由于偏压源对等离子体加热先减弱后增强,导致除了 离子和Cl–离子外,其余带电粒子、O 原子和Cl 原子的密度都是先下降后增加的.此外,随着偏压频率的增加,离子能量分布中的高能峰和低能峰彼此靠近,离子能峰间距变窄,并最终变成单峰结构.本文的结论对于优化等离子体刻蚀工艺具有重要意义.

1 引言

含氯的感性耦合等离子体(inductively coupled plasma,ICP)被广泛应用于半导体产业中,主要有两个原因[1,2]: 第一,采用含氯的等离子体进行刻蚀,能够提高刻蚀的选择性和各项异性;第二,与含其他卤族元素的等离子体相比,采用含氯的等离子体进行刻蚀,易产生挥发性的刻蚀产物.因此,氯和含氯等离子体是半导体(GaAs,GaSb,GaP)、金属(Al,Cu,Pt,Mo,Nb)和含Sr,Bi,Ta,Ba 及Ti 的复合铁电体薄膜材料的最佳刻蚀剂/反应物[3–5].

在过去的几十年中,人们针对Ar,O2,Cl2及其混合气体放电[6–35]进行了大量的研究,尤其重点关注了不同材料的刻蚀速率和选择性[36–47].如Fan等[36]在实验中发现当Ar/O2/Cl2的比例不变时,GaAs 的刻蚀速率随着气体总流速的增加而增加.Smith 等[37]在实验中发现,当在Ar/Cl2混合气体中添加少量的O2后,可以显著地降低AlN 的刻蚀速率,而GaN 的刻蚀速率几乎不变,这显著地提高了AlN 和GaN 之间的选择性.Lee 等[38]和Taube等[39]在Ar/O2/Cl2等离子体放电中,利用X 射线光电子能谱(XPS)发现由于AlGaN 的表面能够形成耐腐蚀的Al2O3层,其刻蚀的选择性高于GaN 和InGaN.Chung 等[40]同样使用XPS 研究了外界参数对在Pt 薄膜上刻蚀TiO2掩膜的影响,结果表明: 在Ar/Cl2混合气体中加入O2会导致Ti2O3和TiO 的氧化,从而降低TiO2的刻蚀速率.2002年,Park 等[41]采用Ar/O2/Cl2等离子体刻蚀SrBr2Ta2O9(SBT) 薄膜,结果表明: O2的加入使SBT 薄膜的结构趋于稳定,进而导致了薄膜刻蚀速率的下降.Kwon 等[42]与Kang 等[43]使用Langmuir 探针研究了Ar/O2/Cl2等离子体中Mo和Al2O3薄膜的刻蚀特性,结果表明: Mo 薄膜的刻蚀速率随着O2含量的增加呈现出非单调的变化,而Al2O3薄膜的刻蚀速率是单调下降的.Tinck等[44–46]用混合等离子体设备模型(HPEM)研究了不同放电条件下Ar/O2/Cl2等离子体对Si 晶圆刻蚀特性的影响,他们发现随着气压和O2气流流速的增加,由于晶圆被氧化,刻蚀速率突然降低并趋于零.Hsu 等[47]在实验中发现当Ar/O2/Cl2混合气体的总流速不变时,Ru 的刻蚀速率随着O2含量的增加先增加后降低.

此外,人们还研究了外界参数对Ar/O2/Cl2等离子体特性的影响.例如,Efremov 等[48]使用Langmuir 探针以 及光发射谱(optical emission spectroscopy,OES)研究了不同的Ar/Cl2(O2比例恒定) 和Ar/O2(Cl2比例恒定) 比例对等离子体状态的影响,结果表明: 即使Cl2的含量低于O2的含量,Cl–离子的密度依然远高于O–离子的密度.Hsu 等[47,49]使用Langmuir 探针等多种诊断工具,发现随着O2含量的增加,电子能量分布函数、等离子体电势和流向器壁表面的离子流仅有微弱的变化.Tinck 等[44–46]使用HPEM 进行模拟,发现虽然刻蚀速率随着O2流速的增加突然降低,但是流向晶圆的粒子通量没有发生突变,即等离子体特性并没有受到显著影响.

在ICP 放电中,为了实现对入射到晶圆上的离子能量和离子通量的独立控制,人们通常会在下电极上施加一个独立的射频偏压源,其中线圈源控制等离子体密度和离子通量,偏压源控制轰击到偏压电极上的离子能量.然而,由于ICP 源和射频偏压源之间存在耦合效应,导致射频偏压源不仅仅会影响偏压电极附近鞘层的振荡行为,还会影响体等离子体的特性.例如,Lee 与Chung[10],Zhang 等[8]和Wen 等[6]分别在实验和数值模拟上发现: 当ICP运行在感性模式时,等离子体密度随偏压功率先降低后增加.Schulze 等[50]在Ne 放电中观察到,即使当ICP 功率远高于偏压源功率时,由偏压源引起的鞘层加热也会对电子的动力学行为产生影响,进而改变体等离子体密度和离子通量.Ahr 等[51]发现当施加射频偏压源时,H2放电中模式转换发生得更为平稳,且随着偏压功率的增加,模式转换发生在较低的ICP 功率下.

尽管人们针对射频偏置的感性耦合等离子体特性进行了研究,但偏压源对Ar/O2/Cl2混合气体放电特性的影响几乎没有报道;另外,入射到偏压电极上的离子能量分布函数(ion energy distribution function,IEDF)在刻蚀过程中也起着非常重要的作用,然而Ar/O2/Cl2感性放电中的相关研究也非常有限.因此,本文将采用由整体模型、鞘层模型和离子蒙特卡罗碰撞(Monte-Carlo collision,MCC)模型组成的混合模型,研究射频偏压源对Ar/O2/Cl2混合气体放电中带电粒子密度、基态中性粒子密度、解离率、电负度以及轰击到偏压电极上的IEDF 的影响.

2 模 型

图1 显示了本文所模拟的腔室结构示意图,其中等离子体区域被分为两部分,即体等离子体区和鞘层区.其中,体等离子体区采用整体模型来描述,即假设等离子体的空间分布是均匀的,各种粒子的密度和电子温度由粒子数平衡方程以及电子功率平衡方程来描述.此外,采用一维流体模型来描述鞘层中带电粒子的产生及输运.当模拟达到稳态后,通过离子MCC 模型来模拟鞘层中离子与中性粒子之间的碰撞过程,进而统计得到电极表面的IEDF.需要注意的是,尽管图1 展示的是二维的腔室结构示意图,但本文所采用的整体模型是零维模型,而用来描述鞘层特性的模型则是一维流体模型.下面详细叙述各模型.

图1 混合模型示意图Fig.1.Schematic of configuration for the hybrid model.

2.1 整体模型

2.1.1 粒子数平衡方程

在Ar/O2/Cl2混合气体中,考虑的粒子种类如表1 所列.对于第l种重粒子(中性粒子和离子),粒子数平衡方程为[6,7,15,16]

表1 Ar/O2/Cl2 混合气体放电中考虑的粒子Table 1.Plasma species considered in Ar/O2/Cl2 discharges.

其中,nl是第l种粒子的密度;L是反应腔室的高度.由于鞘层内的电子密度比较低,在计算体区内的碰撞源项时,需要将最大鞘层厚度ds,max考虑进来.和分别是由于体区反应而引起的第l种粒子的产生和损失项,具体的碰撞过程主要取自文献[6,29–32,35].

Rin,l=4.48×1017Qin,l/V,Rout,l=1.27×10-5nlQin,sum/(p0V)分别是由于气体流入和流出所引起的粒子的产生和损失项.其中,Qin,l是原料气体泵入∑腔室的流速,V表示腔室的体积,Qin,sum=是所有原料气体的入流流速之和,p0是出流处的气压,单位是Torr.由于在实际放电中,只会泵入原料气体,因此泵入源项Rin,l只会出现在原料气体的粒子数守恒方程中.需要注意的是,由于鞘层势垒的作用,负离子只能被约束在放电腔室中心区域,即气体泵出而引起的损失Rout,l只会影响中性粒子和正离子的密度[30–32,52–55].

方程(1)中的最后两项表示粒子在器壁表面上的产生和损失,包括正离子在器壁上的中性化、中性原子的复合以及激发态或亚稳态在器壁表面的淬灭 (退激发)[52,55,56].中性粒子l在器壁上的损失系数为[52]

其中A是腔室的表面积;Λl,Dl,νl和γl分别是中性粒子的扩散长度、扩散系数、热速度和复合/淬灭系数.在Ar/O2/Cl2放电中,各个中性粒子的复合系数γl,如表2 所列.其中,Cl 原子在器壁表面的复合(反应1)系数γl是由腔室的器壁材料以及氯原子和基态氯气分子的密度比值决定的.本文中假设腔室的器壁为不锈钢,则该反应的系数为[29,57]

表2 中性粒子与器壁的相互作用[6,29–32,35]Table 2.Reactions of neutral species on the wall[6,29–32,35].

反应2 的系数主要由氧气的含量决定[32,57,58]:

正离子在器壁表面的损失系数为[52]

其中,Aeff,+=2πRLhR,++2πR2hL,+是离子损失的有效面积,R是腔室的半径,hR,+和hL,+分别是径向和轴向的鞘层边缘与中心处的密度之比[29,30,32].玻姆速度的表达式为

其中,e是单位电荷;M+是离子质量;αs是鞘层边界处负离子密度与电子密度之比,即鞘层边界处的电负度[59].γ-=Te/T-是电子温度Te与负离子温度T-的比值.本文假设负离子温度T-和正离子温度T+是气压p(mTorr) 和背景气体温度Tgas(K)的函数[15,16,54,60]:

需要注意的是,尽管在一般条件下,腔室的外壁不会变得很热(通常在300—330 K 之间),但是放电中心处的气体温度可能较高,尤其当ICP 处于感性放电模式时.因此,背景气体的温度由下式确定[16,24,32]:

其中,〈Pcoil〉=Pcoil/V是线圈的功率密度.

电子密度ne可以通过准中性条件来确定:

其中,q+,n+,q-和n-分别是正负离子的电荷及密度.

2.1.2 功率平衡方程

当放电达到稳定时,等离子体从电源中吸收的功率与等离子体消耗的功率相等.其中,等离子体吸收的功率主要来自线圈功率和偏压源功率两部分;而等离子体消耗的功率主要包括电子和背景气体发生弹性碰撞、激发碰撞和电离碰撞而引起的能量损失,以及带电粒子流向器壁、介质窗和偏压电极而引起的功率损失.因此,功率平衡方程为[6,7,15,16]

其中,Pcoil是线圈功率,它是一个外部输入参数.Pbias是由偏压源引起的沉积功率,包括偏压源功率、欧姆加热功率和随机加热功率.Pc是单位体积内由于电子和中性粒子发生弹性碰撞和非弹性碰撞而损失的能量[29–32]:

nn是参与碰撞的基态中性粒子的密度,kiz是电子和中性粒子发生电离碰撞的速率系数,εc是每产生一个电子-离子对所引起的能量损失[52].

方程(11)中的Pwall表示带电粒子入射到器壁和介质窗上而引起的功率损失,其表达式为[6,7,15,16]

其中,介质窗的半径R1=13 cm;ε+和εe是每个离子和电子损失的平均动能;是接地电极表面的鞘层电压降.根据无碰撞的Child 定律[52],有,其中是时间平均的鞘层电压降,Abias和Ag分别是偏压电极和接地电极的面积.

方程(11)中的Ploss表示由流向偏压电极表面的正离子引起的能量损失,其表达式为[6,7,15,16]

2.2 流体鞘层模型

当在下电极上施加一个射频偏压源时,偏压电极附近的鞘层属性将发生改变,进而影响等离子体状态.因此,本文在整体模型的基础上耦合鞘层模型,自洽地模拟了偏压源参数对等离子体特性的影响.在ICP中,等离子体密度较高,鞘层较薄,即鞘层厚度远小于偏压电极半径,因此可以采用一维鞘层模型来描述.在鞘层区,假设电子密度nes和负离子密度n-s满足玻尔兹曼分布:

其中,ne和n-分别是整体模型计算得到的体等离子体区的电子密度和负离子密度,等离子体电势Vp被设为0.

鞘层内部的电势φs满足泊松方程:

其中,ε0是真空介电常数.n+s是鞘层内的正离子密度,由连续性方程来确定[61–66]:

u+s为离子速度,由动量守恒方程来确定:

其中,p+s是正离子压强,M是离子和背景气体碰撞引起的动量转移.

如图1 所示,偏压源通过一个隔直电容CB连接到下极板上.为了获得偏压电极上的电势Ve和以及偏压源的沉积功率Pbias,在模型中还需要耦合一个电流平衡方程,即Ii+Ie+Id=Ibias.其中Ii,Ie和Id分别是离子电流、电子电流和位移电流,Ibias是偏压源流向偏压电极的电流[15,16]:

其中,偏压源的电压Vrf表示为

式中,V0是电压幅值,f是偏压源的频率.

由偏压源引起的总功率沉积由下式给出[6,7,15,16]:

其中,τrf是偏压源的射频周期;Pohm是由于电子和中性粒子碰撞而引起的欧姆加热功率;Pstoc是由于鞘层振荡而引起的随机加热功率[52,67].

2.3 离子蒙特卡罗碰撞模型

当整体模型和鞘层模型之间的迭代达到稳定后,可以调用离子MCC 模型计算偏压电极上的IEDF.为了消除统计误差,在调用离子MCC之前,通常在一个周期内将大量的粒子均匀地撒在鞘层模型计算区域的边缘,每种正离子的数量约为106个.随着这些离子被电场力推动以及在碰撞过程的影响下,离子的运动轨迹会发生改变.当离子打到极板上时,记录该离子的能量以及离子速度与极板之间的夹角.当所有的离子都到达极板时,即可统计得到归一化的IEDF,记作F(εi)[34]:

其中,nein 是统计IEDF 时对应的离子能量的格点数;N(εi) 是能量介于εi到εi+dε的离子数量;νx,νy和νz分别是子速度在x,y和z三个方向上的分量.离子蒙特卡罗碰撞模型中具体考虑的碰撞过程来自于文献[6,7,18,19,68,69].

3 结果与讨论

3.1 偏压幅值和频率对等离子体特性的影响

若无特殊说明,后文研究条件一致: ICP 功率100 W,气压10 mTorr,腔室的半径和高度均为15 cm.不同偏压源频率下,基态中性粒子密度随偏压幅值的演化,如图2 所示.其中,偏压幅值的变化范围为10—400 V,偏压源频率分别为2.26,6.78,13.56 和27.12 MHz,标准状况下气体流速分别为Ar/O2/Cl2=50/20/100 mL/min.研究结果显示: 在固定的偏压频率下,随着偏压幅值的增加,Ar 原子、O2分子和Cl2(ν=0)分子的密度先快速降低,后缓慢下降/几乎保持不变,最后再次快速降低;ClO 分子的密度则是先快速下降,后几乎保持不变/略微增加,最后再次显著下降;而O 原子和Cl 原子的密度则是先快速增加,随后几乎保持不变/略有增加,最后再次快速增加.此外,偏压频率越低,基态中性粒子密度的中间平稳过渡期越长.另外,当偏 压幅值小 于200 V时,Ar 原子、O2分子,Cl2(ν=0)分子以及ClO 分子的密度随着偏压频率的增加而降低,而O 原子和Cl 原子的密度随偏压频率的增加而提高.当偏压幅值在200—300 V 内变化时,各种中性粒子的密度随着偏压频率先几乎保持不变,随后原料气体密度和ClO 分子密度下降,O 原子和Cl 原子的密度增加.继续提高偏压到400 V,Ar 原子、O2分子、Cl2(ν=0)分子以及ClO 分子的密度随着偏压频率的增加先增加后降低,而O 原子和Cl 原子的密度则随着偏压频率先降低后增加.

图2 不同偏压频率下,基态中性粒子密度随偏压幅值的变化Fig.2.Evolutions of the densities of ground state neutral particles with bias voltage for different bias frequencies.

图3 给出了不同的偏压频率下,吸收功率和损失功率随射频偏压的演化.当偏压频率固定为2.26 MHz 时(图3(a)),随着偏压幅值的增加,从偏压源中吸收的功率Pbias先是以约0.6 倍的增长速率增加,然后增长速率增加为1.7;而由等离子体流向偏压电极引起的功率损失Ploss先是略微增加,后以约0.6 倍的增长速度增加.因此随着偏压幅值的增加,从偏压源中吸收的净功率∆P=Pbias-Ploss先快速增加,后保持不变,最后更为明显地增加.这表明当偏压从10 V 增加到200 V时,等离子体从偏压源中吸收了较多的能量,导致更多的Ar 原子、O2分子和Cl2(ν=0)分子发生非弹性碰撞,增强了O 原子和Cl 原子的产生,如图2(d)和图2(e)所示;当偏压幅值增加到约300 V时,偏压源对净吸收功率几乎没有影响,这导致了O 原子和Cl 原子的密度几乎保持不变;当偏压进一步增加到400 V时,等离子体从偏压源中吸收的能量再次快速增加,从而产生了更多的O 原子和Cl 原子.

图3 不同偏压频率下,吸收功率和损失功率随偏压幅值的变化(a) 2.26 MHz;(b) 6.78 MHz;(c) 13.56 MHz;(d) 27.12 MHzFig.3.Evolutions of the power deposition and power loss with bias voltage for different bias frequencies: (a) 2.26 MHz;(b) 6.78 MHz;(c) 13.56 MHz;(d) 27.12 MHz.

当偏压源频率为6.78 MHz (图3(b)),偏压幅值在10—200 V 范围内时,等离子体从偏压源中吸收的净功率 ∆P仅略微高于2.26 MHz 时的结果,因此O 原子和Cl 原子的密度也略高(见图2).而当偏压幅值增加到300 V时,这两个偏压频率下等离子体吸收的净功率∆P几乎相等,即偏压频率对等离子体的特性几乎没有影响.进一步增加偏压到400 V,偏压频率为6.78 MHz 时的净吸收功率∆P反而低于2.26 MHz 的结果,这导致了电子与原料气体的非弹性碰撞被减弱,从而抑制了O 原子和Cl 原子的产生(见图2(d)和图2(e)).当偏压频率进一步提高到13.56 和27.12 MHz时,偏压源对等离子体的加热更为有效,这促进了O 原子和Cl 原子的产生,并使得原料气体的密度进一步降低.

图4 给出了不同偏压频率下,ClO 分子的主要产生项和损失项随偏压幅值的变化.研究结果表明: ClO 分子最主要的产生途径是Cl 原子在器壁上的复合,并且其反应速率随着射频偏压的增加而增加;ClO 分子最主要的损失途径是电子碰撞解离.随着偏压幅值的增加,电子密度上升(见图5(i)),因此电子碰撞解离ClO 分子的反应速率随之提高,最终导致ClO 分子密度的降低.

图4 不同偏压频率下,ClO 分子的产生速率和损失速率随偏压幅值的变化(a) 2.26 MHz;(b) 6.78 MHz;(c) 13.56 MHz;(d) 27.12 MHzFig.4.Evolutions of the generation and loss rates of ClO molecules with bias voltage for different bias frequencies: (a) 2.26 MHz;(b) 6.78 MHz;(c) 13.56 MHz;(d) 27.12 MHz.

图5 不同偏压频率下,带电粒子密度随偏压幅值的变化(a) Ar+;(b) ;(c) O+;(d) O–;(e) ;(f) Cl+;(g) Cl–;(h) ClO+;(i) 电子密度Fig.5.Evolutions of the densities of charged species with bias voltage for different bias frequencies: (a) Ar+;(b) ;(c) O+;(d) O–;(e) ;(f) Cl+;(g) Cl–;(h) ClO+;(i) electron density.

图5 给出了不同偏压频率下,带电粒子密度随偏压幅值的变化规律.研究结果显示: 当偏压频率较低时,如2.26 和6.78 MHz,随着偏压幅值从10 V 增加到400 V,除了Cl–和ClO+离子密度是先增加后降低最后再增加,以及电子密度是先增加后略微下降,最后再增加外,其余带电粒子的密度都是先增加后基本保持不变/略微增加,最后再继续增加.为了解释Cl–和ClO+离子密度随偏压变化的不同趋势,图6 和图7 分别给出了二者的源项.结果表明: Cl–离子最主要的来源是电子解离附着Cl2(ν=0)分子.如图2(c)和图5(i)所示,当偏压小于200 V时,尽管Cl2(ν=0)分子密度随着偏压的增加而下降,电子密度的增加趋势更为显著,因此Cl–离子的产生速率以及密度都是增加的;当偏压进一步升高到300 V时,一方面由于电子密度和Cl2(ν=0)分子密度略微降低,使得Cl–离子的产生速率下降;另一方面在偏压幅值为200—300 V 的范围内,离子的密度几乎没有受到偏压的影响,导致Cl–离子的损失几乎保持不变.最终,以上两个因素使得Cl–离子的密度呈下降趋势;当偏压继续增加到400 V时,同样是由于电子解离附着Cl2(ν=0)分子的反应速率显著增加,使得Cl–离子的密度随之提高.

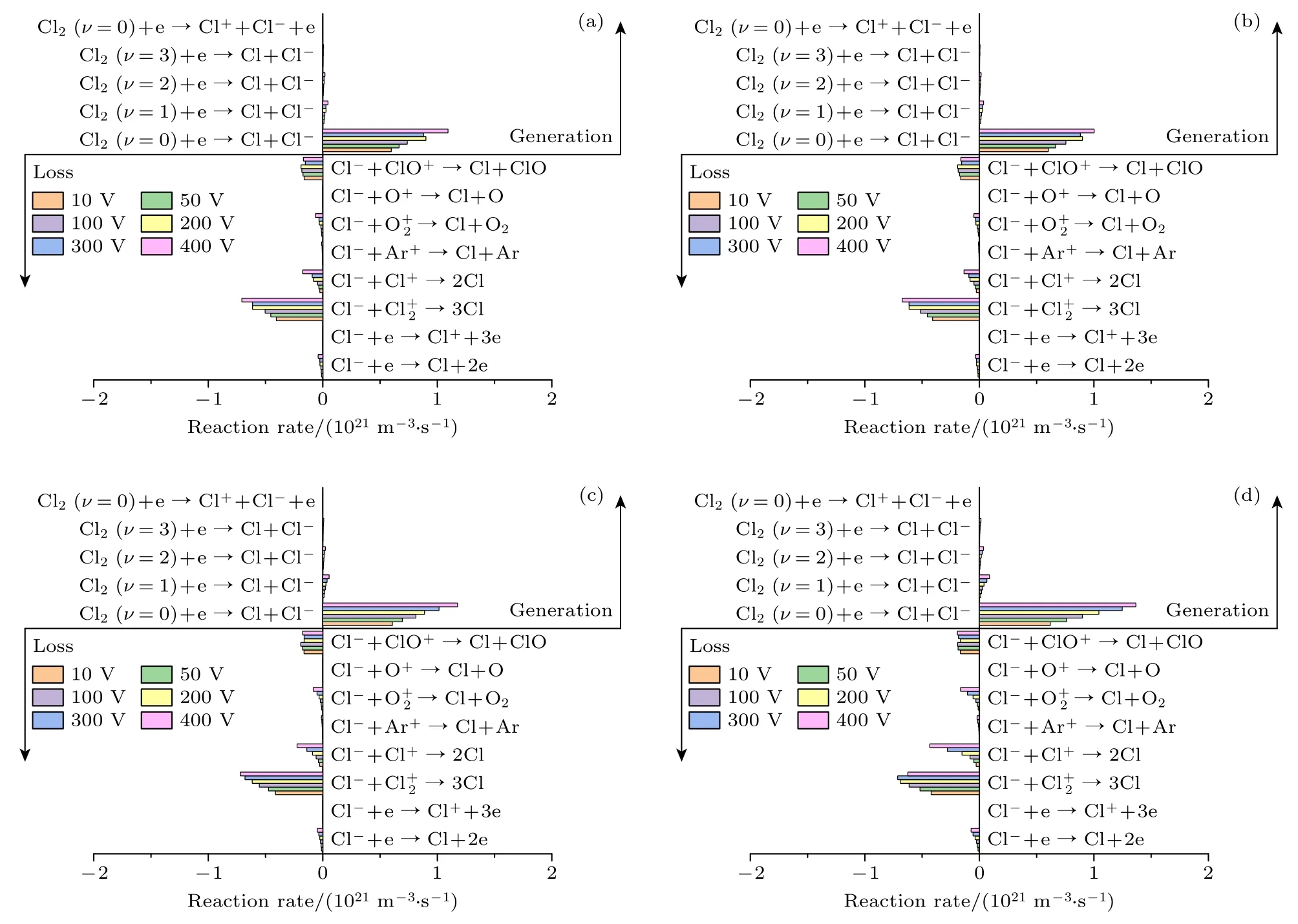
图6 不同偏压频率下,Cl–离子的产生速率和损失速率随偏压幅值的变化(a) 2.26 MHz;(b) 6.78 MHz;(c) 13.56 MHz;(d) 27.12 MHz Fig.6.Evolutions of the generation and loss rates of Cl– ions with bias voltage for different bias frequencies: (a) 2.26 MHz;(b) 6.78 MHz;(c) 13.56 MHz;(d) 27.12 MHz.

图7 不同偏压频率下,ClO+离子的产生速率和损失速率随偏压幅值的变化(a) 2.26 MHz;(b) 6.78 MHz;(c) 13.56 MHz;(d) 27.12 MHzFig.7.Evolutions of the generation and loss rates of ClO+ ions with bias voltage for different bias frequencies: (a) 2.26 MHz;(b) 6.78 MHz;(c) 13.56 MHz;(d) 27.12 MHz.

不同偏压幅值和频率下,ClO+离子的产生率和损失率如图7 所示.显而易见,ClO+离子最重要的产生途径是ClO 分子和离子之间的电荷交换碰撞.以偏压频率为2.26 MHz 为例,当射频偏压增加到150 V时,该碰撞过程的速率变高,导致ClO+离子的密度出现相同的变化趋势(图5(h)).随着偏压幅值进一步增加到300 V,偏压对ClO分子和离子的影响都比较微弱(见图2(f)和图5(e)),因此ClO+离子的产生速率微弱增加.另外,ClO+离子的主要损失途径为在器壁表面的中性化以及与Cl–离子的中和反应.尽管后者的速率随着偏压的增加而降低,但此时ClO+离子的密度较高(见图5(h)),即器壁上的损失过程显著增强.因此,ClO+离子的总损失速率是增加的,最终导致ClO+离子密度的降低.随着偏压增加到400 V,由于此时Cl+离子的密度较高(图5(f)),Cl+离子与ClO 分子之间的电荷交换碰撞速率显著增加,最终导致ClO+离子密度的继续增加.

如图5 所示,当偏压频率增加到13.56 MHz时,随着偏压幅值的增加,除了Cl–离子密度(见图5(g))先线性增加后降低,然后再增加,最后再降低外,其余离子的密度随偏压幅值的变化趋势与低偏压频率时的结果相似.Cl–离子密度随偏压幅值的非单调变化趋势依然可以通过图6(c)中的源项来解释.在前三个阶段中,在电子和离子的共同作用下,Cl–离子密度呈现出先增加、后降低、再增加的趋势;而最后一个阶段,可能是由于此时的Cl–离子密度较高,使得由中和反应引起的损失速率有所提高,如Cl-+Cl+→2Cl,最终导致Cl–离子密度出现短暂的下降趋势.

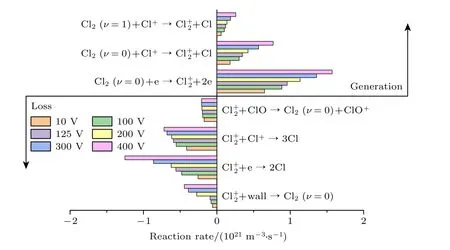
图8 偏压频率为27.12 MHz时, 离子的产生速率和损失速率随偏压幅值的变化Fig.8.Evolutions of the generation and loss rates of ions with bias voltage at bias frequency of 27.12 MHz.

当ICP 功率为100 W,气压为10 mTorr,偏压频率不同时,Cl2(ν=0)分子的解离率nCl/和O2分子的解离率随偏压幅值的变化规律如图9 所示,其中nO∗=nO+nO(D),并且忽略了O2分子的密度.研究结果表明: 当偏压频率为2.26 MHz时,Cl2(ν=0)分子和O2分子的解离率随着偏压先增加,后基本保持不变,最后再继续增加.由图3(a)可知,随着偏压从10 V 增加到200 V,等离子体从偏压源中吸收功率的增长速度快于损失功率,这促进了Cl2(ν=0)和O2的解离(见图2(b)和图2(c)).进一步增加偏压到300 V,由于净吸收功率∆P基本保持不变,Cl2(ν=0)和O2的解离率也近似为一个常数.当偏压增加到400 V时,由于净吸收功率∆P的再一次显著增加,促进了Cl2(ν=0)和O2的解离.此外,当偏压幅值小于200 V时,解离率随着偏压频率的增加而变得更高;当偏压幅值在200 到300 V 的范围内时,解离率随偏压频率先几乎保持不变,然后增加;当偏压幅值高于300 V时,解离率随着偏压频率先降低后增加.另外,还可以发现Cl2(ν=0)分子的解离率始终在45%以上,远高于O2分子(解离率不超过15%).

图9 不同偏压频率下,解离率随偏压幅值的变化(a) Cl2(ν=0);(b) O2Fig.9.Evolutions of the dissociation fraction with bias voltage for different bias frequencies: (a) Cl2 (ν=0);(b) O2.

图10 给出了不同偏压频率下,等离子体的平均电负度α=n-/ne随偏压幅值的变化规律.研究结果表明: 固定偏压频率为2.26 MHz时,等离子体平均电负度随着偏压的增加先快速降低,后基本保持不变,最后再继续下降.需要注意的是,Cl–离子的密度比O–离子的密度高一个数量级(见图5(d)和图5(g)),因此等离子体的平均电负度主要由Cl–离子密度和电子密度的比值决定,即α=nCl-/ne.在较低和较高的偏压范围内,尽管Cl–离子的密度和电子密度都随偏压幅值的增加而增加,但是由于等离子体从偏压源中获得的净能量显著增加,Cl2(ν=0)分子的密度降低(图2(c)),使得Cl–离子的增长速度受到抑制(见图5(g)),因而等离子体平均电负度随偏压幅值的增加呈下降趋势.

图10 不同偏压频率下,电负度随偏压幅值的变化Fig.10.Evolution of the electronegativity with bias voltage for different bias frequencies.

提高偏压频率到6.78 MHz,当偏压小于200 V时,虽然电子密度和Cl–离子的密度都有所增加,电子密度的增幅更显著,因此电负度随偏压频率的增加而降低.当射频偏压在300 V 以上时,虽然电子密度和Cl–离子的密度都有所降低,电子密度的降幅更明显,导致在此偏压范围内,等离子体的平均电负度随偏压频率也有所提高.当进一步提高偏压频率到27.12 MHz时,电子密度和Cl–离子的密度都显著增加,尤其是电子密度,导致了电负度的进一步降低.

3.2 偏压幅值和频率对离子能量分布的影响

在固定的ICP 功率和气压下,偏压频率和幅值对轰击到偏压电极上的Ar+离子的能量角度分布的影响,如图11 所示.研究表明: 当偏压源频率由2.26 MHz 增加到27.12 MHz时,高能峰和低能峰逐渐向中间靠拢,离子能峰宽度∆ε+逐渐减小.这是因为当偏压源频率较低时,离子渡越鞘层的时间τ+远小于射频周期τrf,即离子更能响应鞘层的振荡,从而IEDF 展示出更宽的双峰分布[70],这与Hopkins 等[71]和Gahan 等[72]的测量结果相吻合.随着偏压频率的增加,离子渡越鞘层的时间τ+与射频周期τrf变得相当,这使得离子能峰间距∆ε+变窄,甚至在较低的射频偏压下近似呈现单峰分布,这与Edelberg 等[73–75],Hayden 等[71]和Gahan等[72]的实验测量和Wen 等[6]的数值模拟结果相符.另外,随着偏压幅值的增加,所有的离子能峰均向高能方向移动,且离子能峰宽度∆ε+逐渐增大.这是因为在较低的偏压幅值下,离子运动速度较慢,离子渡越鞘层的时间τ+较长,即IEDF 对射频调制的响应较弱.随着偏压幅值的提高,时间平均的鞘层电压降不断增加,如表3 所列,因此离子获得的能量较高,即离子能峰向高能方向移动;此外,尽管时间平均的鞘层厚度也有所增加,但是的增加更为明显,因此离子渡越鞘层的时间τ+下降,即鞘层振荡对IEDF 的调制作用变得更为明显,离子能峰宽度∆ε+增加.

表3 偏压频率为13.56 MHz时,不同偏压幅值下的时间平均鞘层厚度和鞘层电压降Table 3.Time-averaged sheath thickness and voltage drop across the sheath for different bias voltage amplitudes,at bias frequency of 13.56 MHz.

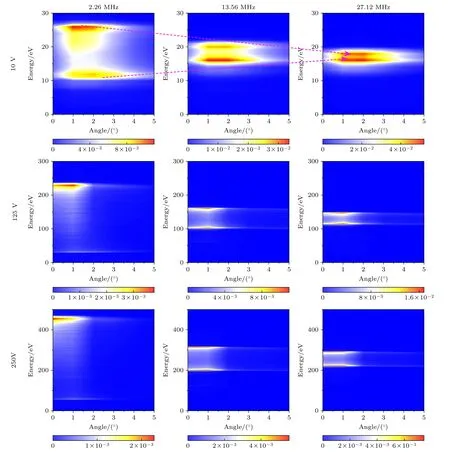
图11 不同偏压频率和幅值下,Ar+离子的离子能量角度分布Fig.11.IEADFs of Ar+ ions for different bias frequencies and bias voltages.

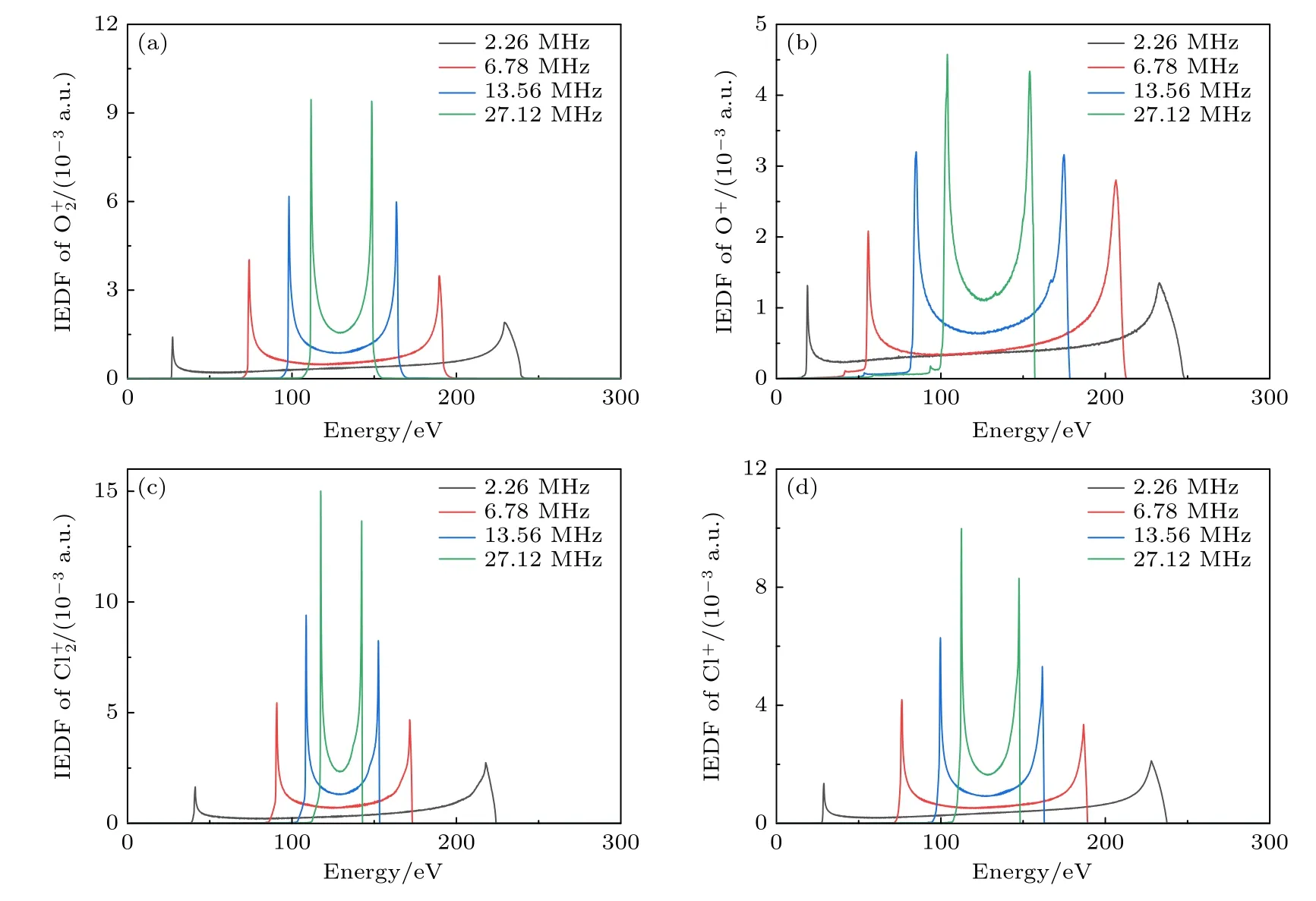
图12 偏压幅值为125 V,不同偏压频率下各离子的能量分布(a) ;(b) O+;(c) ;(d) Cl+Fig.12.IEDFs of ions for different bias frequencies at bias voltage of 125 V: (a) ;(b) O+;(c) ;(d) Cl+.

4 结论

本文采用由整体模型双向耦合鞘层模型、离子MCC 模型组成的混合模型,研究了带有偏压源的感性耦合Ar/O2/Cl2等离子体特性.在ICP 功率为100 W,气压为10 mTorr时,探讨了偏压频率和幅值对基态中性粒子密度、带电粒子密度、解离率、电负度和偏压电极上的IEDF 的影响.

研究结果表明: 当偏压频率为2.26 MHz,偏压幅值低于50 V时,Cl2(ν=0)分子的密度最高;当偏压高于50 V时,Cl 原子取代Cl2(ν=0)分子成为密度最高的中性粒子,离子和Cl–离子分别是最重要的正负电荷携带者.另外,随着偏压幅值的增加,除了Cl–离子和ClO+离子的密度先增加后降低再增加外,其余带电粒子、O 原子和Cl 原子的密度均是先增加后基本保持不变最后再增加.这一现象可以通过等离子体从偏压源中吸收的功率以及在偏压电极上耗散的功率来解释: 沉积功率随着射频偏压单调增加,且在较高的偏压幅值下增幅更明显,而耗散功率先是几乎保持不变随后线性增加.因而,在较低和较高的偏压范围内,等离子体能够吸收更多的能量,这增强了电子与O2分子以及Cl2(ν=0)分子的分解、电离等碰撞过程,并导致O 原子、Cl 原子和带电粒子的密度显著增加.

随着偏压频率的提高,在低偏压范围内,原料气体和ClO 分子的密度以及电负度降低,带电粒子、O 原子和Cl 原子的密度以及解离率增加;在高偏压范围内,原料气体和ClO 分子的密度以及电负度先增加后降低,除了离子和Cl–离子的密度非线性变化外,其余带电粒子、O 原子和Cl原子的密度以及解离率先降低后增加;并且在频率为27.12 MHz,偏压超过250 V时,电子取代Cl–离子成为主要的负电荷携带者.另外,当偏压频率为13.56 MHz时,除了Cl–离子的密度随着偏压幅值先增加后降低再增加最后再降低外,其余粒子密度随偏压的变化趋势与低频结果相似.当偏压频率为27.12 MHz时,除了离子随偏压幅值先快速增加后缓慢增加最后再降低外,其余粒子密度的演化趋势与13.56 MHz 的结果相似.

由于离子能量在刻蚀工艺中具有重要意义,本文还研究了偏压源参数对轰击到偏压电极上的IEDF 的影响.随着偏压幅值的增加,高能峰和低能峰都向高能方向移动,并且离子能峰宽度变宽.另外,随着偏压频率的增加,两个离子能峰逐渐向中间靠拢,能峰宽度逐渐变小,最终由双峰结构变成单峰结构.研究结果有助于我们深入理解带有偏压源的感性耦合Ar/O2/Cl2等离子体的特性,这对于优化等离子体工艺具有重要意义.