结合源偏倚和权窗的蒙特卡罗全局减方差方法*

张显 刘仕倡 魏军侠 李树 王鑫3) 上官丹骅

1) (北京应用物理与计算数学研究所,北京 100094)

2) (华北电力大学核科学与工程学院,北京 102206)

3) (中国工程物理研究院高性能数值模拟软件中心,北京 100088)

全局计数问题在反应堆pin-by-pin 模型蒙特卡罗模拟和多物理耦合计算中动态粒子输运蒙特卡罗模拟等重大研究领域中都有广泛的应用场景.大量的全局减方差算法研究立足于全局计数误差分布的展平,由此提高全局计数的整体效率.本工作针对两种高效全局减方差算法,即均匀计数密度算法(属于源偏倚算法的一种)和权窗算法的结合展开研究,提出利用均匀计数密度算法的偏倚因子调整权窗下限,由此实现两种算法的有机结合.基于Hoogenboom-Martin 压水堆全堆基准题中开展了一系列对比测试,验证了混合全局减方差算法更优于单一权窗算法或均匀计数密度算法,尤其是在降低最大误差方面.同时,基于新的指标,验证了均匀计数密度算法较经典的均匀裂变源算法具有更好的表现.研究结果表明,本文提出的混合全局减方差算法能高效求解全局计数问题,进一步促进了相关领域的研究.

1 引言

蒙特卡罗(Monte Carlo,MC)方法具有几何建模能力强、物理过程描述高保真等优点,被广泛应用于定态和动态粒子输运问题的模拟.随着研究的深入,输运问题的几何模型愈加精细,考虑的因素越来越多,例如反应堆pin-by-pin 模型[1,2]和多物理耦合计算中大规模动态粒子输运模型等[3].庞大的几何和计数规模以及高效高精度的计算需求,给MC 粒子输运模拟带来巨大挑战.由于所模拟系统的空间不均匀性,计数统计误差在全局范围内呈现不均匀分布,由此带来整体效率的低下.解决这一问题的本质困难在于高功率区域因具有较多的粒子样本数,能较快获得统计收敛的结果,而低功率区域的收敛则耗时巨大,仅单纯增加样本总数,只会导致绝大部分计算资源浪费在已收敛的高功率区域,难以(在有些情况下是不可能的)获得全局收敛的计数结果,而这些结果对于反应堆计算或高置信度多物理耦合计算至关重要.

为实现全局计数整体误差分布的展平,需要引入相关的全局减方差算法指导MC 粒子输运,提高全局计数的整体效率[4,5].均匀裂变源(UFS)算法[6–8]是针对临界计算提出的一种高效全局减方差算法,根据裂变中子源的密度分布重新分配裂变源,以便在低功率区域人为地产生更多的裂变中子.基于UFS 算法的启发,均匀计数密度(UTD)算法[9]被提出,其利用目标计数密度来指导源粒子的偏倚,获得了更高的全局减方差性能.此外,权窗(WW)算法[10,11]也是一种被广泛应用的全局减方差算法,不同于UTD 和UFS 算法,WW 算法是对粒子的输运过程进行偏倚,以引导粒子输运到更广泛的区域.

为进一步提高MC 临界计算全局计数问题的整体效率,本文提出一种结合UTD 算法和WW算法的混合全局减方差方法,其利用UTD 的偏倚因子动态调整WW 下限,利用WW 减小UTD 方法引起的权重波动,以此实现两种算法的有机结合.这一方法在MC 粒子输运程序cosRMC[12–14]上进行了验证.第2 节介绍了UFS 和UTD 算法的基本思想;第3 节对混合算法的思想和实现方法进行了描述;第4 节基于新的指标深入研究了UTD算法的效率,并开展混合算法的测试验证;第5 节给出了相应结论.

2 UFS 和UTD 算法原理

在反应堆模拟计算中,不同几何栅元间的功率密度会有较大差异,全堆中子样本数量就会呈现不均匀分布,导致全局计数不能同步收敛.UFS 算法的基本思想: 在保证结果无偏的前提下,对裂变中子源分布进行调整.由于MC 方法进行临界计算是以迭代形式开展的,上一代产生的次级裂变中子将作为下一代的裂变中子源.基于这一特点,UFS算法根据当前代的裂变中子数密度分布产生偏倚因子,在下一代开始时指导裂变源分布的调整.为便于描述裂变中子源分布,在堆芯区域叠加均匀网格对空间进行离散,以网格为单元执行源粒子的偏倚.UFS 偏倚因子的设置方法为

其中,Nt为总裂变源中子数,m为总网格数,Ni为网格i内的裂变源中子数.

引入源偏倚因子βi后,网格i内每次碰撞产生的裂变中子数[15]将被调整为

其中,w是发生碰撞的中子权重;υ为平均次级裂变中子数;为宏观裂变中子截面;是宏观总截面.为保证计算结果无偏,下一代裂变源中子的权重ws将调整为ws/βi.

上述算法将导致低功率区域分裂出更多的小权重中子,而高功率区域则相应减少了裂变中子数,因此不会增加额外的计算耗时.如果减方差目标是展平某种全局计数的统计误差分布,以目标计数密度指导源粒子的偏倚可能比基于裂变中子数密度的偏倚效率更高[9].基于此,UTD 算法提出偏倚因子的设定方法为

其中Tt为所有网格目标计数值之和;m为总网格数;Ti为网格i的目标计数值.上述两种算法本质上都是源偏倚算法.

3 基于UTD 和WW 的混合全局减方差算法

WW 算法是一种基于分裂和轮盘赌的全局减方差方法,也需要借助网格来为不同空间区域提供WW.每一个网格的WW 由三个参数组成,包括WW 上限、WW 下限和轮盘赌存活权重.每当粒子到达栅元边界、碰撞点以及飞行每个平均自由程后,都会对粒子的权重进行检查.如图1 所示,如果粒子权重低于WW 下限,就会触发轮盘赌机制,有效地截断小权重的粒子;如果粒子权重高于WW 上限,对粒子执行分裂操作,增加粒子样本数.通过为低功率区域设置较小的WW 参数,为高功率区域设置较大的WW 参数,可以实现计算资源的均匀分配.WW 算法是一种输运过程偏倚算法.

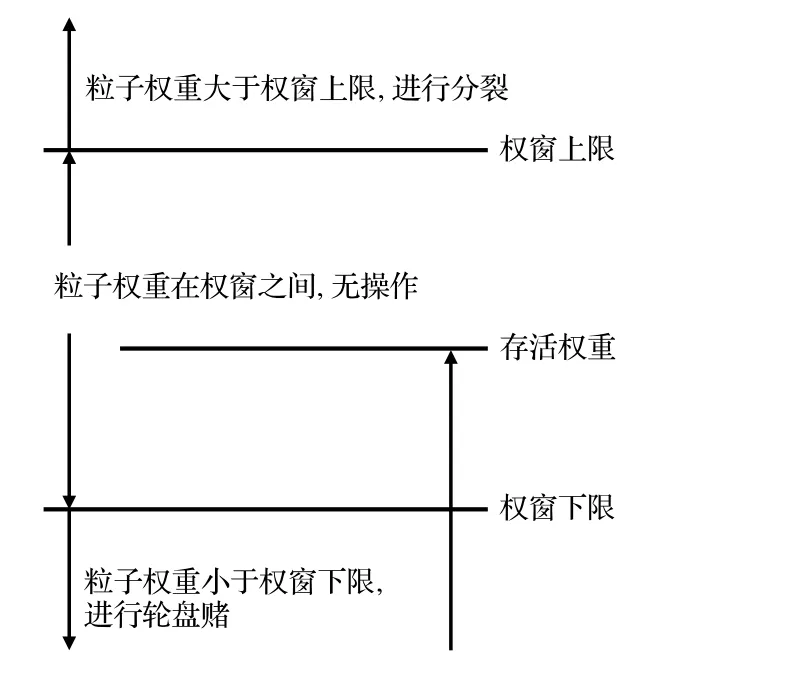
图1 权窗原理Fig.1.Working principle of weight window.

为结合源偏倚与输运过程偏倚各自的优势,获得临界计算全局计数整体效率的进一步提高,本文提出一种基于UTD 和WW 的混合算法.由于UTD 算法会改变裂变中子的权重,可能会引起较大的粒子权重波动,不利于统计结果的整体收敛,而WW 算法可以将粒子权重控制在合理范围内,因此混合算法预计可以获得更高的整体效率.

UTD 方法和WW 方法均基于网格执行偏倚操作,因此在混合算法中两者可以共用一套网格划分方案.在低功率区域,UTD 和WW 方法都会分裂中子,混合算法将建立两个临时储存库,对这些粒子进行临时分类存放,按序完成所有粒子的输运模拟.由于UTD 算法在低功率区域会分裂出极小权重的中子,WW 的轮盘赌机制可能直接截断这类粒子,对UTD 算法的效果造成一定削弱.因此,提出使用UTD 偏倚因子βi来调整网格WW 下限WL:

通过这种方法,在不同功率区域根据UTD 偏倚因子,合理地降低或抬高WW 下限,可以减少WW对UTD 性能的负面影响,实现两种方法的有机结合.

4 数值结果及分析

选择在Hoogenboom-Martin 压水堆全堆基准题[16,17]上开展相关的测试验证.如图2 所示,该模型堆芯径向半径为209 cm,轴向高度为366 cm,共包含241 个燃料组件,燃料组件为 17×17 布置;每个组件内呈现17×17 的棒分布,包含264 个燃料棒和25 个控制棒通道.从图2(a)和图2(b)(不采用任何全局减方差算法)可以看出,基准模型的径向功率分布具有显著不均匀性,导致统计误差分布也呈现严重不均.将堆芯沿横向和纵向划分成289×289 的网格,其中燃料区网格共计69649 个.计算条件为非活跃代数200,活跃代数300,每代初始粒子数50000,采用50 核并行计算,统计每个网格的中子裂变功率.

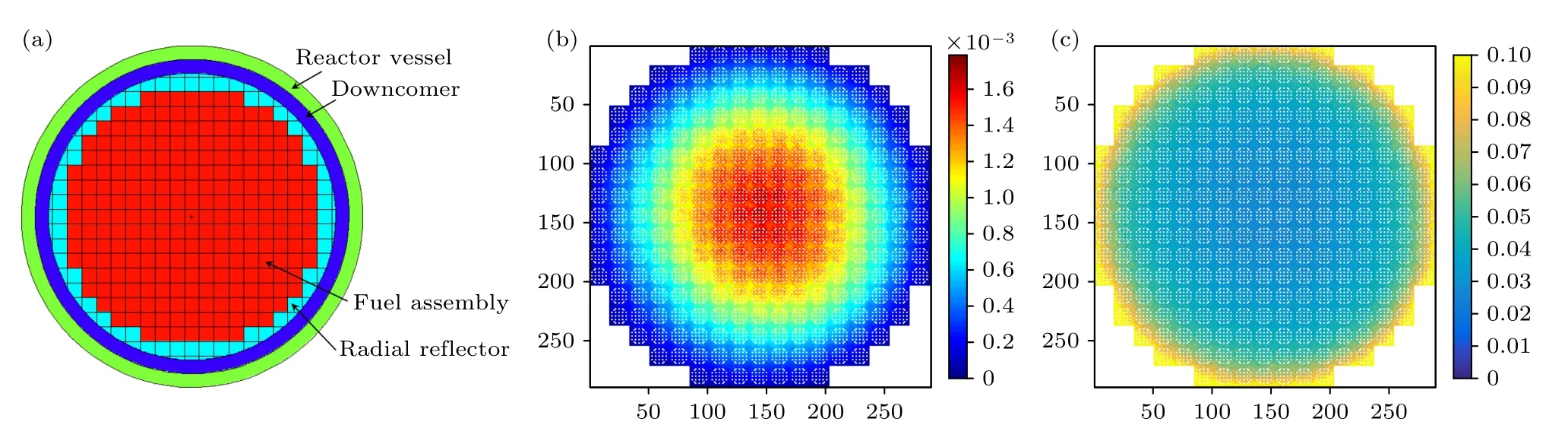
图2 Hoogenboom-Martin 基准题(a) 几何横截面;(b) 功率分布(MW);(c) 统计误差分布Fig.2.Hoogenboom Martin benchmark: (a) Geometric cross-section;(b) power distribution (MW);(c) statistical error distribution.

4.1 基于新指标的UTD 和UFS 对比分析

为更清晰地了解UTD 算法的优势所在,基于新指标对UTD 和UFS 进行了对比分析.在H-M基准题计算中,堆芯模型具有1/4 对称性,4 个对称区域的物理量在理想情况下应完全相同,而由于统计误差的存在,导致堆芯物理对称区域的计算结果略有不同,称之为计算不对称性.引入变异系数Cυ定量描述这种计算不对称程度,变异系数越大表示不对称性程度越大[18]:

其中,S和分别是对称区域4 个计数量的标准偏差和平均.

图3 给出了Basic,UFS 和UTD 三种情况下的变异系数分布.从图3 可以看出,不使用任何源偏倚的Basic 情况下,堆芯外围的计算不对称程度明显比中心的不对称程度大;使用UFS 算法时,堆芯外围的Cυ明显降低,计算不对称程度较Basic的小;UTD 算法下的计算不对称度相较UFS 有了更进一步的改善.

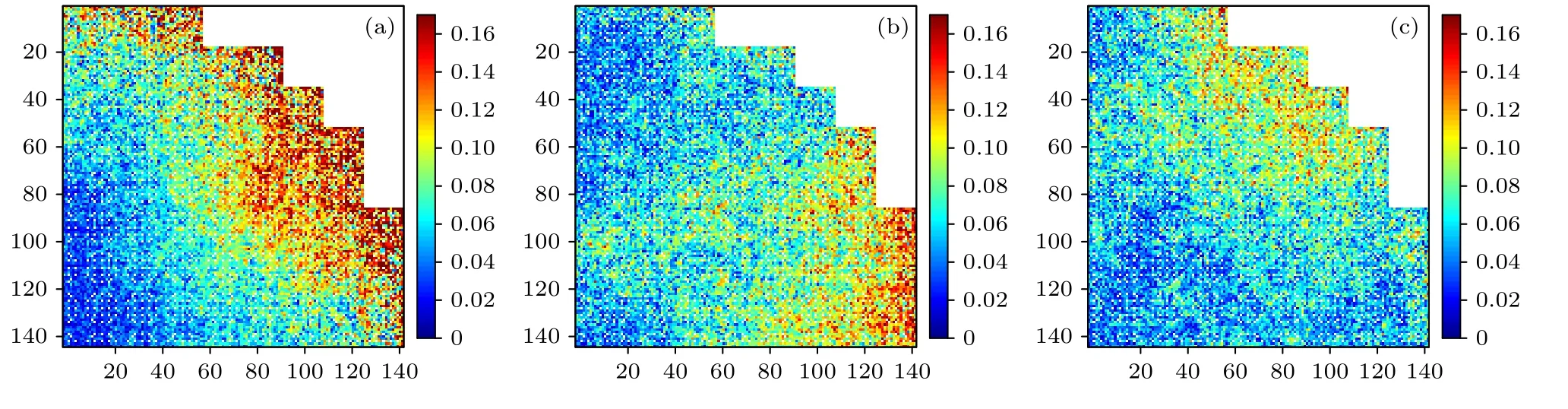
图3 变异系数分布(a) Basic;(b) UFS;(c) UTDFig.3.Distribution of the coefficient of variation: (a) Basic;(b) UFS;(c) UTD.

此外,UFS 算法和UTD 算法在临界计算的每个活跃代都会对偏倚因子进行更新,选取了堆芯中横向289 个连续的网格,计算得到UTD 和UFS算法在这些网格中的偏倚因子的方差分布,见图4.UTD 偏倚因子的方差整体小于UFS 偏倚因子的方差,UTD 算法的偏倚因子在迭代过程中波动更小,表明UTD 算法相比UFS 算法更具稳定性.

图4 偏倚因子的方差分布Fig.4.Variance distribution of bias factors.

为了进一步对比两者的减方差效果,引入品质因子FOM_MAX 和FOM_95 来表征计算效率[19,20]:

这里,T是计算时间,Remax是所有网格计数的统计误差的最大值,Re95表示某一网格计数的统计误差,其使至少95%的网格计数的统计误差都不大于该值.表1 给出了三种计算条件下中子注量率的统计误差和品质因子.从两种品质因子来看,UTD 算法和UFS 算法均获得了计算效率的提高,并且UTD 算法的计算效率略优于UFS 算法.在降低最大误差的问题上,UTD 算法的计算效率是UFS 算法的1.36 倍.

表1 UTD 算法和UFS 算法的计算结果对比Table 1.Comparison of calculation results of UTD and UFS.

4.2 混合算法的验证

统计误差的累积分布如图5 所示,UTD 算法下的统计误差较集中落在3.7%—5.0%区间内,混合算法和WW 算法下的统计误差较集中落在2.7%—3.2%区间内.从结果可以看出,WW 算法下的统计误差整体小于UTD 算法,且最大和最小误差的差值相比UTD 算法也更小,说明WW 算法的减方差力度比UTD 算法更大.使用混合算法时,UTD 算法会在临界计算中的每个活跃代开始对裂变源分布进行调整,WW 算法会在粒子输运过程中对粒子进行偏倚,两者的共同作用使得低功率区域具有更多的粒子样本,在低功率区域实现更进一步的减方差效果,从而混合算法的最大统计误差小于WW 算法和UTD 算法.表2 列出了三种减方差算法的整体效率,通过品质因子可以得出,针对降低最大误差的问题,混合算法的计算效率分别是WW 算法和UTD 算法的2.6 倍和3 倍.

表2 计算结果对比Table 2.Comparison of calculation results.

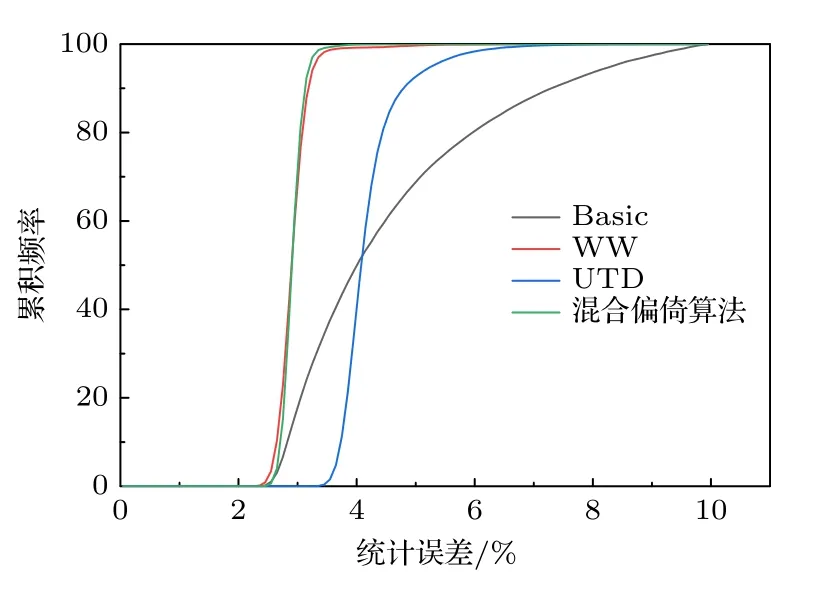
图5 统计误差的累积分布Fig.5.Cumulative distribution of statistical errors.

5 结论

围绕MC 粒子输运模拟全局计数问题统计误差分布不均的问题,本文提出了一种结合均匀计数密度算法和WW 算法的混合算法,通过引入WW减少了均匀计数密度算法导致的权重波动,其WW 下限利用均匀计数密度算法偏倚因子进行调整,本质上实现了源偏倚和输运过程偏倚的有机结合.在Hoogenboom-Martin 基准题的验证计算中,基于新的指标对比分析了均匀计数密度算法和UFS 算法,进一步验证了UTD 算法的高效性.同时,计算结果表明,混合算法的整体效率较均匀计数密度算法或WW 算法有进一步的提高.在降低最大误差方面,混合算法的整体效率分别是WW算法和均匀计数密度算法的2.6 倍和3倍,验证了混合算法的优越性.