双振荡场产生正负电子对的理论研究*

李传可 林南省 周鲜鲜 江淼 李英骏‡

1) (中国矿业大学(北京),隧道工程灾变防控与智能建养全国重点实验室,北京 100083)

2) (中国矿业大学(北京)理学院,北京 100083)

3) (安徽财经大学管理科学与工程学院,蚌埠 233030)

在强电磁场下真空产生正负电子对的研究中,多场的组合扮演重要的角色.本文运用计算量子场论方法在全时空数值求解狄拉克方程,研究了两个空间分离的局域化振荡电场击穿真空产生正负电子对的过程.结果表明通过选取合适的场参数,两场的相互作用可以显著增强正负电子对的产生.两场的相互作用使产生正负电子对的动量分布曲线出现了周期性的振荡,并导致了非对称的多光子跃迁过程.通过含时微扰理论分析得出,正负电子对的动量分布的周期性振荡可由电场宽度、电场频率和两场间距共同决定.两场间距能够改变正负电子对动量分布的变化周期,随着两场间距的增大,产生正负电子对的动量(能量)的单一性得到优化;电场宽度不仅影响正负电子对动量分布的峰谷高度差,还会改变其在动量空间峰值的展宽;根据能量守恒定律,电场频率的增大使得产生粒子对的动量随之变大.因此,通过选择合适电场参数可以抑制或加强特定动量分布的正负电子对,这为今后的实验设计提供了重要的理论指导.

1 引言

量子电动力学(QED)在理论上精准地预测了真空在超强电磁场的作用下会衰变产生正负电子对[1,2].早期开创性的研究可追溯到Sauter[3]以及Heisenberg 和Euler[4]的研究.1951年,Schwinger[5]使用固有时的方法计算了均匀静电场下真空中正负电子对的产生率w ∝exp(-Ec/E),Ec表示真空产生正负电子对所需的临界电场强度,Ec=1.32×1018V/m;E表示外加电场的强度.因此,将真空通过量子隧穿产生正负电子对的过程称为Schwinger 机制或Schwinger 效应.1970年,Brezin以及Itzykson[6]利用Wentzel-Kramers-Brillouin(WKB)近似的方法将真空产生正负电子对的研究扩展到随时间变化的空间均匀电场,并发现了基于多光子跃迁的正负电子对产生过程.除了上述方法外,世界线瞬子方法[7–9]、量子Vlasov 方程(QVE)[10–13]、Dirac-Heisenberg-Wigner (DHW)形式[14–19]和计算量子场论(CQFT)[20–33]等方法被广泛应用于正负电子对产生的研究.此外,研究者们对不同方法之间的关系进行了探讨,因为它不仅可以相互验证彼此的结果,而且有助于从不同角度理解他们的结果.例如,Dumlu[34]在标量QED 和旋量QED 中证明了QVE 与半经典散射方法的等价性.Hebenstreit 等[14]发现旋量QED 中的Wigner 函数可以简化为具有单分量且空间均匀的含时电场的QVE.Li 等[35]将上述结果推广到标量QED,并发现此时电场可以有3 个分量.Li 等[36]从理论上证明了对于空间均匀的电场CQFT 等价于QVE.

近年来,随着激光技术的飞速发展[37],激光强度已经达到1023W/cm2.并且更高强度的激光设施仍在建设中,如欧洲的极端光基础设施[38].这极大地激发了人们对真空中产生正负电子对的研究热情.实验方面,人们通过高强度的激光与物质相互作用产生γ光子,再利用产生的γ光子与激光光子相互作用,通过Breit-Wheeler 过程来产生正负电子对[39–44].但是这种通过两步过程实现正负电子对产生的实验设计,依然需要先与物质相互作用.若仅有激光相互作用产生正负电子对所需要的激光强度[5]为1029W/cm2.目前最高的激光强度与之相比仍差几个数量级.2008年,Schützhold 等[8]提出了一种动态辅助的Schwinger 机制,由一个强而缓慢变化的电场和一个弱而快速变化的电磁场相结合.动态辅助的Schwinger 机制显著提高了正负电子对产生的概率,并导致正能连续态与Dirac海之间有效谱间隙的缩小.从极端光基础设施的结构特点出发,提出了多脉冲同时聚焦于一点的方案[45–48].与单脉冲的情况相比,该方案使得实验上观测到真空产生正负电子对的阈值能量显著降低.Jiang 等[21,24]设计了一个多场结构,通过将几个局域的次临界静电场并排应用,显著降低了量子隧穿产生正负电子对的阈值.但是,两个局域化的振荡电场之间的相互作用如何影响正负电子对的产生有待进一步的研究.本文从两个对撞激光脉冲所形成的驻波场出发构建两个局域化的时空不均匀的电场,并结合微扰理论分析了电场宽度、电场频率以及电场间距对正负电子对产生过程的影响.研究结果可以为真空产生正负电子对的实验研究提供理论指导.

2 理论方法与模型

2.1 计算量子场论

采用计算量子场论的方法[20–33]研究极强电场下真空中正负电子对的产生过程,该方法可以在全空间和时间上数值求解狄拉克方程.由于单粒子的量子力学方程不足以描述粒子的产生和湮灭,在量子场论的框架下,引入含时的场算符.场算符随时间的演化过程由海森伯运动方程描述,其中标量场描述的一维哈密顿量H^=cσ1p+σ3c2+V(z,t),σ1和σ3为泡利矩阵,c为真空中的光速,V(z,t) 为外场对应的势能.除无特殊声明外,将沿用原子单位制(ℏ=m=e=1,c=137.036).将外加电场当作经典场,并忽略粒子之间的相互作用,因此这里海森伯方程等价于狄拉克方程:

本文采用的外场是沿z方向分布的,狄拉克方程的4 旋量波函数简化成了2 旋量波函数.对于自由哈密顿量H0=cσ1p+σ3c2,其本征态有up(z)(E≥c2)和un(z)(E≤–c2).那么,场算符可以表示为

式中,∥vac〉〉表示真空态.这意味着,ρ(z,t) 表示电场突然关闭后产生的电子的空间分布.最后,对空间密度在全空间进行积分,得出每一时刻的粒子产生总数:

式中,Upn(t) 表示时间演化矩阵,表示t时刻的负能量态un(z,t) 在自由正能量态up(z) 上的投影,对应跃迁概率,即

产生电子的动量分布表达式为

利用能量和动量的关系E2=c4+c2p2可以得到产生电子的能量分布.最后,利用劈裂算符和快速傅里叶变换数值求解狄拉克方程,即可得到(5)式中的Upn(t),进而得到相关的可观测量.

2.2 外场模型

采用两个局域化的时空不均匀电场,两个电场是空间分离的.电场用标势V(z,t) 表示,其表达式为

式中,电场的空间部分为

V1=V2是电势的高度,W1=W2是电场的宽度,z0是电场的中心,d表示两个电场中心的距离.电场宽度为激光脉冲的半高宽,为了使两个电场在空间上是分离的,须满足d>2W1.另外,ω 表示振荡场的振荡频率.

2.3 一阶含时微扰理论

为了深层次理解两个振荡场的相互作用对正负电子对产生过程的影响,本文采用一阶含时微扰理论进行分析.首先,将哈密顿量分成两部分:H=cσ1p+σ3c2+V(z,t)=H0+H′.其中,H0=cσ1p+σ3c2是自由哈密顿量,H′=V(z,t) 是微扰部分.对于自由哈密顿量,通过其狄拉克方程H0|Ψ〉=E|Ψ〉,解得正能量本征值Ep=负能量本征值En=本征值对应的本征矢有:

式中,sgn(p)和sgn(n)分别表示动量p和动量n的符号.任意时刻t的一阶微扰的跃迁幅值可以表示为

将标势(7)式和自由哈密顿量的本征函数(8)式代入(9)式并积分,可以得到:

式中,V0表示电场的高度且V0=V1=V2,W表示电场的宽度,W=W1=W2,p,n表示动量,Ep和En为相应动量的能量,Apn是由(9)式的内积项给出:

通过对所有p 态和n 态求和,可以得到正负电子对产生总数的一阶微扰估计值:

产生正负电子对的动量分布,通过对所有n 态求和,可得

3 结果与讨论

我们运用计算量子场理论和一阶含时微扰理论研究了两个振荡场中正负电子对的产生.接下来将主要讨论两个振荡场之间的相互作用对正负电子对产生的影响,以及电场宽度、电场频率和两场间距在正负电子对产生过程中所扮演的角色.

3.1 场间的相互作用对正负电子对产生的影响

通过多光子跃迁效应产生的正负电子对,振荡场的频率ω 起决定性作用.由于所选的振荡场频率ω=2.5c2大于正负能级之间的能量间隙2c2,无论是单振荡场还是双振荡场都以一个稳定的速率产生正负电子对,如图1 所示.其中两场间距d=8/c,而电场宽度(激光脉冲的半高宽)W1=W2=3/c,能够使电场的主要产生区域在空间上分离.通过对比计算量子场论结果和微扰结果可知两者符合较好,最大相对误差不超过4.02%.因此,微扰理论能够很好地描述通过单光子跃迁产生正负电子对的过程(微扰理论的适用性将在附录中进一步讨论).并且两种结果均以T/2 的周期在时间上振荡,微扰理论的结果(12)式中的高频振荡项Ep–En+ω 是正负电子对的数量在时间上振荡的原因.电场振荡项sin(ωt)在一个周期内会有向上和向下两次取到最大振幅的过程,因此正负电子对的数量在时间上的振荡周期为T/2.此外,还发现双振荡场产生的正负电子对数量超过了单振荡场产生正负电子对数量的2 倍.两场间的相互作用导致正负电子对产生数量的增加,说明双振荡场的正负电子对产生过程具有增益效应.

图1 正负电子对数量随时间的变化,实线和虚线分别表示计算量子场论的结果和一阶含时微扰理论的结果,蓝色线表示双振荡场产生的粒子对数量,黑色线表示单振荡场产生的粒子对数量,红色点线表示单振荡场产生的粒子对数量的2倍,其 中V1=V2=0.75c2,W1=W2=3/c,d=8/c,ω=2.5c2,T=2π/ωFig.1.Time evolution of the electron-positron pairs,the results calculated by the computational quantum field theory and the first-order time-dependent perturbation theory are represented by the solid line and the dashed line,respectively.The electron-positron pairs created by double oscillating filed is represented by blue line,the electronpositron pairs created by single oscillating field is represented by black line,and the twice of the pairs created by single oscillating field is represented by the red dotted line.Here,V1=V2=0.75c2, W1=W2=3/c,d =8/c,ω=2.5c2,T =2π/ω.

为了进一步分析双振荡场正负电子对产生过程的增益效应,我们研究了产生的正负电子对的动量分布.利用微扰理论计算了20 个激光周期时所产生正负电子对的动量分布,如图2 所示,发现与计算量子场论的结果符合得很好.可以看到,由于两个场的相互作用,双振荡场产生粒子的动量分布在动量p=±103.7 附近的展宽变窄,有利于产生单一能量的正负电子对.另外,双振荡场产生粒子的动量分布曲线出现了振荡,在动量p=±53.4和p=±138.2 处出现了新的峰值,在动量p=±69.1 和p=±128.8 处出现了新的谷值.这里,峰值与谷值对应正负电子对动量分布的极值点.当某一动量上的正负电子对数量是局部最大值时,定义为动量峰值;反之,定义为动量谷值.尽管计算量子场论和一阶含时微扰理论的动量峰值强度在动量p=±53.4 和p=±138.2 处并未有明显的差距(图2),但两者之间的相对误差为4.17% (p=±53.4)和3.33% (p=±138.2),如表1 所列.然而在动量p=±103.7 处的计算量子场论和一阶含时微扰理论的动量峰值强度差距较大(见图2),但仅为7.41%,说明数值模拟与理论推导的较为吻合.

表1 计算量子场论与一阶含时微扰理论的动量峰值强度误差Table 1.Error of momentum peaks probability with the CQFT and the first-order time-dependent perturbation theory.

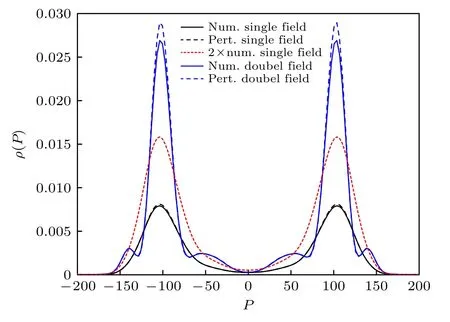
图2 正负电子对的动量分布,实线和虚线分别表示计算量子场论的数值结果和一阶含时微扰理论的结果.其中V1=V2=0.75c2,W1=W2=3/c,d=8/c,ω=2.5c2,t=20T=40π/ωFig.2.Momentum spectra of the created electron-positron pairs,the results calculated by CQFT and the first-order time-dependent perturbation theory are represented by the solid line and the dashed line,respectively.Here,V1=V2=0.75c2,W1=W2=3/c,d=8/c,ω=2.5c2,t=20T=40π/ω.

有趣的是,振荡势阱产生的正负电子对的动量分布也发现了相似的振荡行为[23],其来源于微扰结果中sin2[(p+n)d/2]项.与之不同的是,本文的外场构型为两个空间分离的振荡电场,通过微扰计算得到正负电子对的动量分布(13)式,发现两个空间分离的振荡场所产生正负电子对的动量分布被cos2[(p+n)d/2]调制.在数学上,cos2[(p+n)d/2]=sin2[(p+n)d/2+π/2],两者相比仅差π/2 的相位.假设双振荡电场的相位差ϕ从0 变换到π,外场结构即从双振荡电场变换成了振荡势阱.那么,微扰理论中,cos2[(p+n)d/2]=sin2[(p+n)d/2+π/2],外场结构的相位差也会影响正负电子对的动量分布.

另外,通过对比双振荡场和单振荡场2 倍的动量分布(见图2),由于两个场的相互作用,在动量峰(p=±53.4,±103.7,±138.2)处双振荡场的产生粒子数大于单振荡场的2倍,其中动量主峰(p=±103.7)处双振荡场的产生粒子数是单振荡场的3.4倍,因此双振荡场的正负电子对产生过程具有增益效应.根据能量动量关系E2=c4+c2p2可以得到动量p=±103.7 对应的能量为E=1.25c2.而振荡场的频率ω=2.5c2,根据能量守恒定律Ep=En+ω,负能态En=–1.25c2的电子吸收一个光子的能量跃迁到正能态Ep=1.25c2.这说明一阶含时微扰理论给出的动量分布(13)式中的共振项Ep-En-ω表示产生过程.可以通过一阶含时微扰理论很好地描述正负电子对的产生过程.

3.2 两场间距对正负电子对产生的影响

通过研究不同场间距下产生的正负电子对数量随时间的变化(图3)发现随着场间距的逐渐增加,正负电子对的产生数量会逐渐减少,最终趋于一个稳定值.另外,当场间距足够大(例如d=11/c,14/c)时,与单振荡场产生正电子对数量的2 倍相等,双振荡场的正负电子对数量的增益效应随着场间距的增大而减弱直至消失.

图3 不同场间距d 下正负电子对数量随时间的变化,实线和虚线分别表示计算量子场论的结果和一阶含时微扰理论的结果.其中V1=V2=0.75c2,W1=W2=3/c,ω=2.5c2,T=2π/ωFig.3.Time evolution of the created electron-positron pairs for different distances between the two fields (d),the results calculated by CQFT and the first-order time-dependent perturbation theory are represented by the solid line and the dashed line,respectively.Here,V1=V2=0.75c2,W1=W2=3/c,ω=2.5c2,T=2π/ω.

假设 (12) 式中 cos2[(p+n)d/2] 的(p+n)为常数,那么随着间距d的变化,正负电子对的产生数量应为周期性变化.而研究结果表明无论是量子场论还是微扰理论,正负电子对的产生数量随两场间距d的变化都是单调的(图3).如图4 所示,随着场间距d的增大,因为两场的相互作用,动量主峰(p=±103.7 处)的产生数量减少,并且出现了更多的动量峰值和谷值,从而导致(p+n)无法作为常数考虑.这也是两场的相互作用所导致的增益逐渐减小直至消失的原因.根据微扰理论,两个电场的相互作用由cos2[(p+n)d/2]描述.如果当场间距d较小且p+n≠ 0时,cos2[(p+n)d/2]的振荡周期较大,那么正负电子对的在动量上的宽度相对较宽,如图4 所示.同时,动量主峰(p=±103.7 处)附近的产生概率被大大加强,因此当场间距较小时,正负电子对的产生数量也被相干增强.此外,改变两场的间距d可以改变特定动量下的正负电子对产生率.例如,在动量p=±128.8 和p=±72.3处,d=8/c时为动 量谷值,而 当d=14/c时为动量峰值;在动量p=±47.1处,d=8/c时为动量峰值,当d=14/c时为动量谷值.可以利用这种机制抑制或加强相应能量的粒子产生,从而产生单一化能量的正负电子对.

通过微扰理论,正负电子对的动量分布被cos2[(p+n)d/2]因子控制,随着场间距d的变化,其动量分布的振荡周期也会随之改变.对于d=8/c,11/c,14/c,其动量分布的振荡周期分别为53.8,39.1,30.7.计算量子场论的结果中(见图4),场间距d=8/c,11/c,14/c的动量分布的振荡周期分别为50.3,37.7,31.4,两者符合较好.随着场间距d的增大,正负电子对的动量分布的振荡周期变小,双振荡场产生粒子的动量峰的展宽更窄,并且正负电子对的产生率几乎没有发生改变(见图3),这为产生足够多的单一能量的正负电子对提供了可能.由于正负电子对的动量分布的振荡周期变小,出现了更多的动量峰值和谷值.但是,对于绝对值大于103.7 的动量峰值(当d=8/c,11/c,14/c时,动量峰值分别为p=±138.2,±131.9,±128.8)并不符合cos2[(p+n)d/2]因子所给出的动量振荡周期,即正负电子对的正(负)动量分布并不是关于动量p=103.7(p=–103.7)对称分布的.通过微扰理论计算,当d=8/c,11/c,14/c时,动量峰值分别为p=±157.8,±143.1,±134.7,但这些动量处均未出现动量峰值,如图4 所示.为了进一步分析正负电子对的动量分布曲线的不规则振荡,根据能量动量关系Ep=,和En=,计算了每一动量峰值所对应的能量.发现正负电子对的产生包含两种过程: 对称跃迁过程和非对称跃迁过程.以d=8/c为例,根据能量守恒定律Ep=En+ω,对称跃迁过程有1.25c2=(–1.25c2)+2.5c2,即负能态En=–1.25c2(n=±103.7)上的电子吸收一个光子的能量跃迁到正能态Ep=1.25c2(p=±103.7);而非对称跃迁过程中,动量峰值p=±53.4 对应的能量1.08c2,根据以上能量守恒关系,这些跃迁来自于能量为En=–1.42c2(n=±138.2)的负能态.此外,负能态En=–1.08c2(n=±53.4)还可吸收一个光子跃迁到正能态Ep=1.42c2(p=±138.2),使得跃迁概率在p=±138.2 处出现峰值.最近研究发现造成非对称跃迁的原因是外加电场的空间非均匀性[49].我们使用的双振荡电场之间存在相互作用,使得非对称跃迁在某一动量下被加强或抑制,因此所产生正负电子对的动量分布出现了动量峰值(被加强)和动量谷值(被抑制).因此,动量p=±103.7 上电子来自于对称跃迁过程,其他动量上的电子来自于非对称跃迁过程.而动量p=±103.7 上电子数量远大于其他动量,说明对称跃迁过程更容易发生.

3.3 电场宽度对正负电子对产生的影响

我们所用的电场宽度一致,即W=W1=W2.随着电场宽度W的增大,正负电子对的产生率显著减少,如图5 所示.对于Sauter 型的电势,其电场强度E0=∂V(z,t)/∂z|z=z0=V/(2W) .电势高度保持不变,电场强度随电场宽度的增大而减小,而正负电子对的产生率与电场强度的平方成正比[6],即Γ∝E02.因此,当电场宽度增大时,正负电子对产生率显著减小.

图5 不同电场宽度W 下正负电子对数量随时间的变化,实线和虚线分别表示计算量子场论的结果和一阶含时微扰理论的结果.其中V1=V2=0.75c2,d=14/c,ω=2.5c2,T=2π/ωFig.5.Time evolution of the created electron-positron pairs for different widths of electric field (W),the electronpositron pairs calculated by CQFT and first-order timedependent perturbation theory are represented by the solid line and the dashed line,respectively.Here,V1=V2=0.75c2,d=14/c,ω=2.5c2,T=2π/ω.

微扰理论的(12)式和(13)式表明电场宽度W通过W2csch2[πW(p+n)]因子影响双振荡场中正负电子对的产生数量和动量分布.为了研究W2csch2[πW(p+n)]因子如何影响双振荡场中正负电子对的产生,进一步分析了不同电场宽度下的正负电子对的动量分布.如图6 所示,随着电场宽度的增大,虽然动量主峰p=±103.7 处的正负电子对数量受影响较小,但其他动量峰值对应的粒子数量显著减小,从而导致了正负电子对产生的总数显著减小.此外,电场宽度W=2/c时,在动量p=±147.7 处是动量峰值,而当电场宽度W=4/c时,不再是动量峰值.通过微扰理论的(13)式发现,正负电子对的动量分布与W2csch2[πW(p+n)]项成正比.当电场宽度W增大时,W2csch2[πW(p+n)]项随之减小,每一动量上正负电子对的数量也随之减少(图6).W2csch2[πW(p+n) ]因子不仅改变了正负电子对的动量分布峰值的高度,还改变了动量分布的展宽.因此,在动量p=±147.7处,随着电场宽度W的增大,正负电子对动量分布的峰值逐渐消失.而3.2 节中所提到cos2[(p+n)d/2]项所预测的绝对值大于103.7 的动量峰值没有出现也是因为被W2csch2[πW(p+n)]项所抑制.因此,电场宽度W也可以调节正负电子对的动量分布.若在实验中需产生某一特定动量分布的正负电子对,可以通过调节振荡场频率ω,电场宽度W和两场间距d来实现.

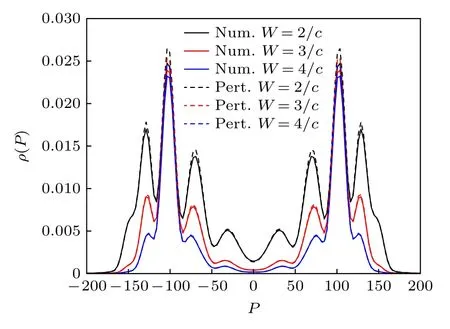
图6 不同电场宽度(W)下正负电子对的动量分布,实线和虚线分别表示计算量子场论的结果和一阶含时微扰理论的结果.其中V1=V2=0.75c2,d=14/c,ω=2.5c2,t=20T=40π/ωFig.6.Momentum spectra of the created electron-positron pairs for different widths of electric field (W),the results calculated by CQFT and the first-order time-dependent perturbation theory are represented by the solid line and the dashed line,respectively.Here,V1=V2=0.75c2,d=14/c,ω=2.5c2,t=20T=40π/ω.

3.4 电场频率对正负电子对产生的影响

通过多光子跃迁机制产生正负电子对的过程中,电场振荡频率有着举足轻重的作用.图7 描述了不同电场频率下正负电子对的产生数量随时间的变化.对于电场频率ω=2.3c2,2.4c2,2.6c2,2.7c2,微扰理论与计算量子场论的结果最大相对误差分别为8.14%,5.40%,2.93%,2.32%,说明微扰理论仍然适用于描述不同电场频率下正负电子对的产生过程.并且随着电场频率ω 的不断增大,正负电子对的产生数量逐渐减少.从微扰的角度上来看,更大的频率会激发出更高能的电子,但是相应的耦合矩阵元 〈p|V|n〉 会随着动量p的增大而减小,因此同时粒子数产量也会跟着减小.

图7 正负电子对数量随时间的变化,实线和虚线分别表示计算量子场论的结果和一阶含时微扰理论的结果.这里,V1=V2=0.75c2,W1=W2=3/c,d=8/c,T=2π/ωFig.7.Time evolution of the electron-positron pairs,the results calculated by the computational quantum field theory and the first-order time-dependent perturbation theory are represented by the solid line and the dashed line,respectively.Here,V1=V2=0.75c2,W1=W2=3/c,d=8/c,T=2π/ω.

根据微扰理论,电场频率主要以[exp(Ep-Enω)-1]/(Ep-En-ω)的方式控制所产生正负电子对的动量分布,即满足共振条件Ep-En-ω=0的量子态之间才能够发生跃迁产生正负电子对.如图8 所示,不同电场频率下所产生的正负电子对过程依然存在对称跃迁和非对称跃迁两种过程,并且两种过程都遵循能量守恒定律.随着电场频率的增大,动量峰值所对应的动量逐渐变大.由于动量的增大,相应的耦合矩阵元 〈p|V|n〉 而减小,因此该动量处正负电子对的产生概率也会随之减小.

图8 不同电场频率下正负电子对的动量分布,实线和虚线分别表示计算量子场论的结果和一阶含时微扰理论的结果.其中V1=V2=0.75c2,W1=W2=3/c,d=8/c,T=2π/ωFig.8.Momentum spectra of the created electron-positron pairs for different frequencies of electric field.The results calculated by the computational quantum field theory and the first-order time-dependent perturbation theory are represented by the solid line and the dashed line,respectively.Here,V1=V2=0.75c2,W1=W2=3/c,d=8/c,T=2π/ω.

4 结论

本文运用计算量子场论方法和一阶含时微扰理论研究了两个空间分离的局域化振荡电场下正负电子对的产生过程,分析了两个振荡场和单一振荡场中正负电子对产生过程的异同,详细讨论了电场宽度、电场频率和两个电场的间距对正负电子对产生过程的影响.研究发现一阶含时微扰理论与计算量子场论结果符合较好,这为研究超临界频率电场的正负电子对产生提供良好的理论工具.两个电场的相互作用会导致正负电子对的动量分布曲线出现振荡行为,并使正负电子对的产生总数有所增加.而随着两电场的间距增大,两场的相互作用导致的增益效应将会减弱直至消失.根据微扰理论,场间距主要通过cos2[(p+n)d/2]项来调控所产生的正负电子对的动量分布,使所产生的正负电子对的动量分布出现周期性振荡行为.并且通过分析正负电子对的动量分布,发现了非对称的多光子跃迁过程.随着电场宽度的增大,电场强度随之减小,正负电子对的产生总数也随之减少.电场宽度以W2csch2[πW(p+n)]的方式调节正负电子对的动量分布,其能够改变正负电子对的动量分布振荡幅值,并同时改变动量分布的展宽.根据能量守恒定律,电场频率的增大使得产生粒子对的动量变大,相应的耦合矩阵元〈p|V|n〉 也随之减少,所产生的正负电子对的数量也随之减小.因此,能够通过改变电场频率、电场宽度、两场间距来加强或抑制某一特定动量上的正负电子对的产生率.这对未来的激光诱导真空产生正负电子对的实验具有一定的理论指导.

附录A 一阶含时微扰理论的适用性

通过一阶含时微扰理论和计算量子场论两种方法讨论了双振荡电场产生正负电子对的过程.其中,一阶含时微扰理论能否有效地描述正负电子对的产生过程显得尤为重要.为了衡量一阶含时微扰理论的适用范围,引入了平均相对误差:

为了确保一阶含时微扰理论能够有效地描述正负电子对的产生,当平均相对误差大于10%时,认为一阶含时微扰理论不再适用于描述真空中的正负电子对产生.我们主要通过控制变量的方式分析了不同电场宽度、电场势高和电场频率下一阶含时微扰理论与计算量子场论的平均相对误差,相应的参数有:W1=W2=3/c,V1=V2=0.75c2,ω=2.5c2,每次测试中仅改变其中的一个参数,如表A1所列.

表A1 计算量子场论与一阶含时微扰理论的产生粒子对数量的平均相对误差Table A1.Mean relative error of the particle number created by the CQFT and the first-order timedependent perturbation theory.

我们发现对于不同电场频率,两者的平均相对误差先增大后减小,在临界频率2c2附近,一阶含时微扰理论失效.根据能量守恒定律,在临界频率附近,在动量p=0 附近所产生的正负电子对最多,所产生的正负电子对会在空间上聚集,由于泡利不相容原理,抑制了正负电子对的产生.我们推测含时微扰理论忽略了空间的影响,不受泡利不相容原理的限制,正负电子对能够持续不断的产生,因此在临界频率附近,两者的平均相对误差较大,一阶含时微扰理论失效.在临界频率附近的正负电子对产生过程还有很多问题值得研究,接下来的工作中,我们将进一步探讨临界频率附近含时微扰理论的适用性.两者的平均相对误差随着电场宽度的增大而减小,当电场宽度小于0.7/c时,一阶含时微扰理论失效.而电场势高的增大会增大两者的平均相对误差,当电场势高大于1.2c2时,一阶含时微扰理论不再适用.这是因为电场强度E=V/(2W),当电场宽度减小或者电场势高增大时,电场强度增大,外加电场不能被当作微扰项,因此当电场宽度小于0.7/c,抑或电场势高大于1.2c2时,一阶含时微扰理论与计算量子场论的平均相对误差较大,含时微扰理论不适用于描述正负电子对的产生过程.