基于改进强耦合振子的微弱脉冲信号检测方法*

李远芳 姜园 赵磊

(中山大学电子与通信工程学院,深圳 518107)

强耦合振子可用于微弱脉冲信号的检测和波形恢复,但其对微弱脉冲信号的检测频率会受到系统内置频率的限制.在系统内置频率固定的情况下,系统只能对一定频率范围内的脉冲信号进行有效检测和波形恢复,在检测更高频率的脉冲信号时会出现波形失真.本文分析了耦合振子内置频率和微弱脉冲信号检测频率之间的关系,提出两种改进强耦合振子结构以扩展微弱脉冲信号的频率检测范围.通过引入非线性恢复力耦合项,非线性恢复力强耦合振子可以有效保留信号的高频分量,在更高频率的脉冲信号输入时也能较好地保留信号特征.双振子强耦合系统通过引入Van der Pol-Duffing 振子,加强了系统内部结构的稳定性,同样达到了扩展脉冲信号频率检测范围的效果.此外,基于变迭代步长和混沌检测的频率相关性,提出了一个未知频率脉冲信号检测方法,以改变迭代步长的方法代替改变系统内置频率来进行频率扫描,并且利用混沌检测的频率相关性,将接收信号和恢复信号的相关系数和纯噪声输入情况下的相关系数进行对比,根据两个相关系数之间的明显差异可以有效检测出脉冲信号.通过仿真实验进行验证,所提方法可以有效检测出未知频率的脉冲信号,并且所提的改进强耦合振子结构相对于强耦合振子有较大的性能提升.

1 引言

随着空间电磁环境日益复杂,对微弱信号的研究也越来越受到重视.微弱信号检测技术在通信、测量、生物医学、海洋和机械工程等领域都有广泛应用,且一直是国内外研究学者关注的研究热点[1−4].传统的微弱信号检测方法主要包括线性方法,如相关检测[5]、谱估计[6]、小波分析[7]等,以及非线性方法,如经验模态分解[8]、高阶累积量[9]等.这些方法的主要目标是通过抑制噪声来提高信噪比,但在噪声抑制的过程中不可避免地会对信号造成损伤,因此在微弱信号处理上,这些方法的性能往往十分有限.相比之下,基于混沌理论的信号检测方法对系统参数摄动具有敏感性,对噪声具有一定的免疫特性,并且所需先验知识较少,能够在各种噪声下应用,因此特别适用于微弱信号检测[10−13].自20 世纪末开始,混沌理论得到了蓬勃发展,许多学者开始将混沌理论应用到微弱信号检测领域,并取得了一系列重要进展.

1992年,Birx 等[14]采用了复映射前向反馈神经网络识别Duffing 方程相平面中的变化,以检测随机高斯噪声背景下的微弱信号.此后,混沌检测得到了不断改进和发展.2009年,Yuan 等[15]将Duffing 振子的相图混沌程度和输入混沌序列的混沌程度相关联,以此实现了对EEG 信号的检测,从而首次将混沌振子的检测范围扩展到非周期性信号.2011年,吴勇峰等[16]发现脉冲信号能够激励环形耦合Duffing 振子之间出现瞬态同步突变现象,并利用这一现象成功检测出强噪声背景下的微弱脉冲信号.2015年,曾喆昭等[17]基于广义时间尺度变换,对Duffing 振子模型进行了扩展,有效扩展了微弱脉冲信号的频率检测范围,提升了检测性能.2016年,张悦等[18]利用自适应算法对双耦合Duffing 振子检测算法进行了改进,并在对瞬态电磁辐射信号进行脉冲展宽处理后,成功实现了瞬态电磁辐射信号的远距离探测.曹保锋等[19]于2019 年发现对两个Duffing 振子同时施加较大的恢复力和阻尼力耦合,可使振子间产生广义的“阱内失同步”现象,并基于这种现象实现了微弱脉冲信号的检测和恢复.2020年,Luo 等[20]提出一个同时具有线性和非线性耦合项的双耦合Duffing系统,并利用该系统实现对复杂不规则信号波形的降噪处理,成功恢复出复杂不规则信号的波形细节和信号总体趋势.

虽然大量的研究表明,混沌振子在微弱信号检测领域具有很大的潜力,但目前基于混沌振子的时域微弱脉冲信号检测技术尚未成熟.强耦合振子虽然能够实现对微弱脉冲信号的检测及波形恢复,但在系统内置频率设定后,强耦合振子只能检测一定频率范围内的脉冲信号,对更高频的脉冲信号检测会出现失真,在实际检测未知频率的脉冲信号时性能十分局限,这极大限制了强耦合振子在实际工程中的应用.针对强耦合振子的不足,本文对强耦合振子进行了改进,提出了两种改进的强耦合振子系统,分别为非线性恢复力强耦合振子和双振子强耦合系统.非线性恢复力强耦合振子通过引入非线性恢复力耦合项,提高了系统对高频分量的保留能力,减少系统在检测高频脉冲信号时的失真,尽可能提高恢复信号波形和接收波形相关性.双振子强耦合系统通过引入Van der Pol-Duffing 振子,利用Van der Pol-Duffing 振子优秀的抗干扰能力和高检测灵敏度,提高系统整体的检测性能,能更好识别脉冲信号对系统的激励,从而提高脉冲信号波形恢复效果.另外,基于变迭代步长方法[21]和混沌检测的频率相关性,本文提出一种未知频率脉冲信号检测方案,通过变迭代步长进行频率扫描,然后求接收信号和恢复信号的相关系数,并和纯噪声情况下的相关系数作对比,可以实现对未知频率脉冲信号的检测.

2 系统振子

2.1 强耦合振子

Holmes 型Duffing 振子是一个经典混沌振子模型,其方程为

单个Duffing 振子只适用于检测微弱周期信号,应用范围十分有限,为了扩展检测信号类型提高检测性能,常将多个振子进行耦合.常见的线性恢复力耦合振子方程[16]如下:

其中,α(x1-x2) 为线性恢复力耦合项,α为耦合系数.线性恢复力耦合振子由两个Duffing 振子通过线性恢复力耦合而成,耦合系数一般较小,默认取值为0.2,所以线性恢复力耦合振子一般也被称为“双耦合振子”或“弱耦合振子”.线性恢复力耦合振子可以通过失同步实现对脉冲信号的检测.在检测脉冲信号时,需要将系统置于同宿轨道,令两个Duffing 振子处于同步状态,然后将信号输入其中一个Duffing 振子,使两个Duffing 振子失同步,通过两个振子之间状态的差异可以检测出脉冲信号.虽然线性恢复力耦合振子能检测脉冲信号的有无,但它无法恢复脉冲信号波形,并且检测性能也十分有限.

2019年,曹保锋等[19]在(3)式的基础上提出了一种强耦合振子,方程为

其中ξk(x1-x2) 为线性恢复力耦合项,k(-)为阻尼力耦合项,k为阻尼力耦合项系数,ξ为阻尼系数.在强耦合系统中,阻尼力耦合系数和线性恢复力耦合系数相关联,并且阻尼力耦合系数k维持在一个比较大的值,通过较大的阻尼力和线性恢复力共同耦合,脉冲产生的激励能同时作用于系统的两个Duffing 振子,使两个Duffing 振子产生方向相反的突变,根据两个Duffing 振子之间的状态差异可以实现脉冲信号的检测和波形恢复.强耦合振子检测脉冲信号的原理如图1 所示,图1(a)为原始三角脉冲信号以及带噪脉冲信号,脉冲幅值为0.6,脉冲宽度为1 μs,上升沿和下降沿相等,均为0.5 μs,信噪比为0 dB.采样时间间隔10 ns,采样持续时间20 μs,系统内置角频率为 5×106rad/s,系统参数为文献[16]中默认参数,本文参数设置借鉴了文献[16]以便于对比,但信号参数设置不失一般性.将图1(a)中的加噪三角脉冲信号输入强耦合振子系统,系统的时域输出和相轨图如图1(c),(d)所示,明显看到两振子同时出现了方向不同的突变,第1 个Duffing 振子相轨图出现了向上的轨道偏移,而第2 个Duffing 振子相轨图出现了向下的轨道偏移,对两个振子输出的一阶微分项进行差分可以恢复出三角脉冲信号,恢复波形见图1(b).

图1 三角脉冲检测示意图(a)原始三角脉冲及加噪三角脉冲;(b)系统恢复的三角脉冲波形;(c)系统两个振子的时域输出;(d)系统两个振子的相轨图Fig.1.Triangular pulse detection diagram: (a) Original delta pulse and noise-added delta pulse;(b) delta pulse waveform after system recovery;(c) time domain output of two oscillators of the system;(d) phase track diagram of two oscillators of the system.

强耦合振子相对于线性恢复力耦合振子,不仅提高了脉冲信号的检测性能,并且实现了对脉冲信号的波形恢复,但强耦合振子在系统内置频率固定后,只能对很窄一个频段范围内的脉冲信号进行有效检测和波形恢复,在输入信号频率过高时,系统恢复的脉冲波形会出现失真,所以在对脉冲信号进行检测时需要预先对待测信号的频率有一个大致估计,这在一定程度上限制了强耦合振子的实际应用.为了更好地说明强耦合振子存在的信号检测频率限制问题,以图1(a)中三角脉冲信号检测为例,设置强耦合振子内置角频率为 106rad/s,其他参数相同,此时强耦合振子的时域输出和恢复的三角脉冲如图2 所示.从图2(a)可以看到,在输入脉冲信号频率相对于系统内置频率过高的时候,输入脉冲信号的脉冲宽度已经小于强耦合振子输出的正弦波周期,此时输入脉冲信号对系统的影响只能让系统在单个正弦周期内出现突变,而这远比在多个周期突变要困难,并且输入信号频率相对于系统内置频率越高,系统突变越困难,此时系统的突变很容易出现失真,使得恢复的信号波形发生畸变.对比图1(b)和图2(b),可以明显看到,在相同的三角脉冲输入下,内置频率更低的强耦合振子输出已经发生畸变,恢复的波形已经不是一个标准的三角脉冲了,这说明在系统内置频率变低之后,已经无法对图1(a)中的三角脉冲实现波形恢复,系统存在一个和内置频率相关的脉冲信号检测频率范围.

图2 强耦合振子对高频三角脉冲检测效果图Fig.2.Effect of strong coupling oscillator on the detection of high-frequency triangular pulse.

2.2 非线性恢复力强耦合振子

为了拓宽检测频率范围,提高信号检测效果,本文提出了非线性恢复力强耦合振子,动力学方程为

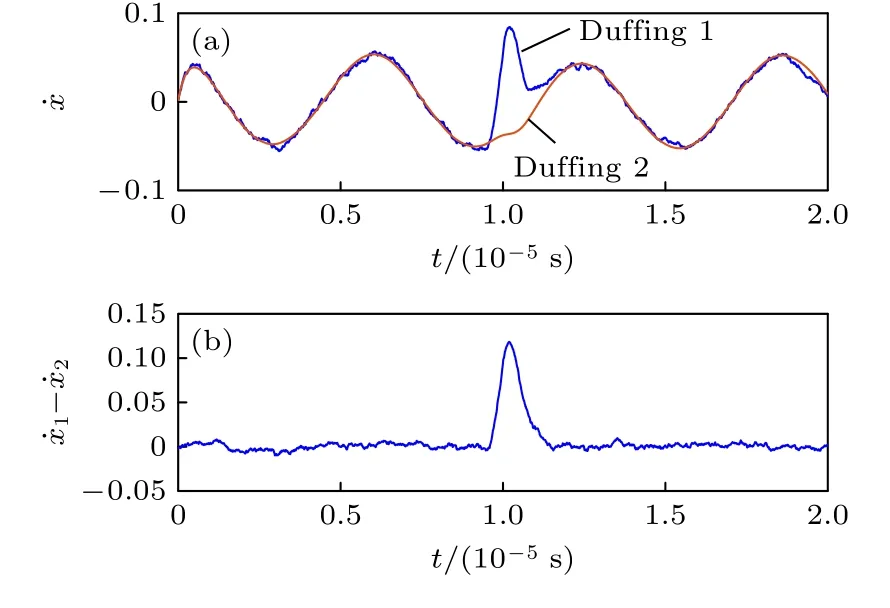
图3 非线性恢复力强耦合振子对高频三角脉冲检测效果图Fig.3.Effect of nonlinear restoring force strong coupling oscillator on the detection of high-frequency triangular pulse.

2.3 双振子强耦合系统

Van der Pol-Duffing 振子是广泛应用于物理学、生物学和力学领域的一种振子模型,动力学方程为

其中,γ为阻尼系数,λ为刚度系数,取值一般为1,F和ω分别为周期极化力的振幅和角频率.鉴于Van der Pol-Duffing 振子对噪声的良好免疫能力,常将Van der Pol-Duffing 振子和Duffing 振子进行线性耦合来提高系统的检测性能.Van der Pol-Duffing 振子和Duffing 振子的线性耦合方程如下:

由于Van der Pol-Duffing 振子和Duffing 振子的线性耦合系统具有优秀的抗干扰能力和检测灵敏度,故基于Van der Pol-Duffing 振子和Duffing振子的线性耦合系统和强耦合振子结构提出双振子强耦合系统.将Van der Pol-Duffing 振子以及Duffing 振子的线性耦合系统作为一个整体,然后将两个线性耦合系统进行强耦合,双振子强耦合系统方程如下所示:

式中有3 个耦合项,d1(x1-y1) 为Van der Pol-Duffing 振子和Duffing 振子的线性耦合系统内部的线性耦合项,d2(x1-x2) 为两个线性耦合系统之间的线性耦合项,d3(x˙1-x˙2) 为两个线性耦合系统之间的阻尼力耦合项,d1,d2和d3分别为对应耦合项的耦合系数.双振子强耦合系统通过两个线性耦合系统之间的线性耦合和阻尼力耦合维持强耦合振子的检测机制,并通过内部的线性耦合d1(x1-y1)来引入Van der Pol-Duffing 振子特性,提升系统抗噪声干扰能力,提高系统检测灵敏度.双振子强耦合系统检测脉冲信号的机制与强耦合振子相同,都是通过脉冲信号的激励使两个Duffing 振子之间出现同步突变,然后利用两个Duffing 振子的状态差异来检测和恢复脉冲信号.为了更好对比说明双振子强耦合系统的优势,同样以图1(a)中的三角脉冲信号检测为例,设置系统参数:F=0.2,ξ=2.78,γ=2,d1=0.2,d2=16,d3=3.4,内置角频率为106rad/s,此时双振子强耦合系统的时域输出和恢复的三角脉冲如图4 所示.对比图2 和图4 可以看到,双振子强耦合系统在当前频率脉冲信号输入下,能恢复出标准的三角脉冲信号,这说明双振子强耦合系统能检测到更高频率的脉冲信号,双振子强耦合系统相对于强耦合振子有着更广的脉冲信号检测频率范围.和非线性恢复力强耦合振子保留脉冲信号高频分量不同,双振子强耦合系统的优势在于利用了Van der Pol-Duffing 振子的特性来提升检测性能,Van der Pol-Duffing 振子的优秀抗干扰特性体现在其同步状态更不容易被破坏,输出更加稳定.对比图3(a)和图4(a),可以看到在脉冲信号的激励下,非线性恢复力强耦合振子的两个Duffing 振子为正常的反向突变,而双振子强耦合系统第2 个Duffing 振子甚至出现了和第1 个Duffing 振子同向的突变趋势,这在一定程度上带来的好处是,双振子强耦合系统能对更高频的信号进行检测,并且拥有更优秀的抗噪声干扰能力,在检测瞬态脉冲信号时有更好的检测性能.从图3(a)和图4(a)可以看到,双振子强耦合系统的时域输出比非线性恢复力的时域输出更加平滑,从图3(b)和图4(b)可以看到,双振子强耦合系统恢复的三角脉冲比非线性恢复力强耦合振子恢复的三角脉冲更能保留原三角脉冲的信号特性.

图4 双振子强耦合系统对高频三角脉冲检测效果图Fig.4.Effect of dual-oscillator strong coupling system on the detection of high-frequency triangular pulse.

3 未知频率脉冲信号检测方法

为了进一步分析不同耦合系统对脉冲信号检测频率范围的影响,本文采用皮尔逊相关系数作为衡量系统检测性能的指标,皮尔逊相关系数可以反映系统恢复的脉冲信号波形和原始脉冲信号波形的相似程度,其定义为

其中,X和Y分别为输入和输出信号序列,Xi和Yi分别为输入和输出信号序列中第i个值,和分别为X和Y的均值,r为X和Y的相关系数,取值范围为[–1,1],r=0 表示X和Y无相关性,负值表示负相关,正值表示正相关,r的值越大表示相关程度越高.为了比较各个耦合系统对不同频率的脉冲信号波形恢复程度,固定耦合系统内置频率为100 Hz,然后将不同频率的周期三角脉冲信号输入耦合系统,求耦合系统恢复的脉冲信号与原始脉冲信号的相关系数.采样率采用0.1 MHz以保证每个系统都能有足够多的采样点来进行波形恢复.各个系统恢复信号与原始信号的相关系数随检测信号频率变化的曲线图如图5 所示.图5 中相关系数大于0.9 视为系统可以较好恢复出信号波形,可认为此时恢复信号接近原始信号,所以将相关系数大于0.9 以内的频率范围视为耦合系统的脉冲信号检测频率范围.

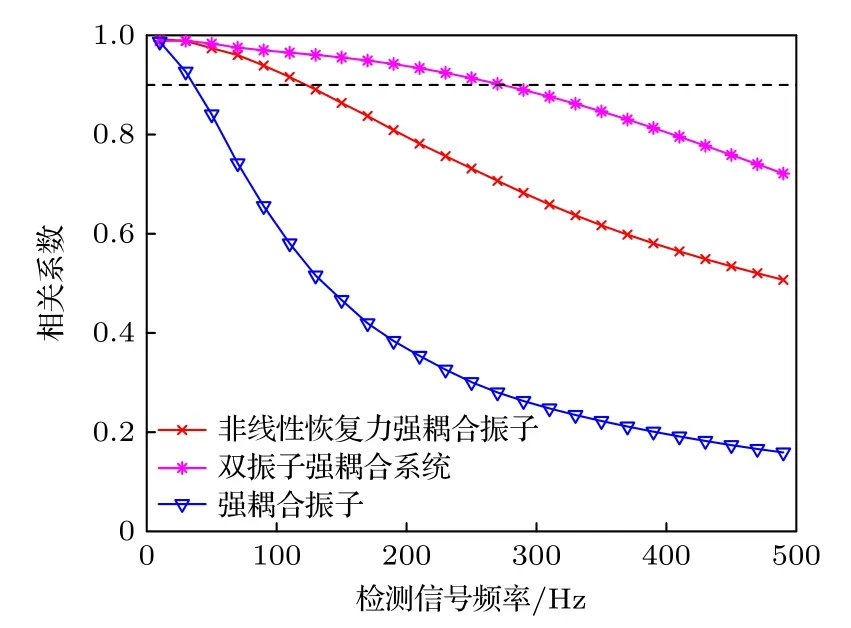
图5 原始信号和耦合系统恢复信号的相关系数随检测信号频率变化曲线图Fig.5.Curves of correlation coefficients of the original signal and the recovered signals of the coupled systems with the frequency of the detected signal.

由图5 可以看到,不同强耦合系统对脉冲信号的检测特性一致,固定系统内置频率后,除了信号频率过低,检测点不够导致无法进行相关的部分,曲线总体变化趋势为: 输入脉冲信号频率越低,系统对脉冲信号的恢复效果越好;输入脉冲信号频率越高,系统对脉冲信号恢复效果越差.这是因为在输入脉冲信号的频率较低时,脉冲信号对系统的激励能让振子在多个正弦周期发生突变,脉冲信号的幅度变化能最大程度传递到振子中,使两个振子突变产生的状态差异能较好反映输入脉冲信号特征.在输入脉冲信号的频率较高时,脉冲信号对系统的激励只能让振子在单个正弦周期内发生突变,这会加大振子突变的难度,振子产生的突变会丢失部分脉冲信号特征,所以恢复信号会失真.非线性恢复力强耦合振子和双振子强耦合系统分别通过引入非线性恢复力耦合项和引入Van der Pol-Duffing振子,分别通过不同的方式扩展了脉冲信号检测频率范围,提高脉冲信号检测性能.由图5 可以看到,在系统内置频率为100 Hz 的情况下,强耦合振子只能检测34 Hz 以内的脉冲信号,才能令恢复信号和原始脉冲信号的相关系数达到0.9,而非线性恢复力强耦合振子可以较好恢复出125 Hz 以内的脉冲信号波形,双振子强耦合系统则可以对270 Hz以内信号实现良好检测.这里将系统内置频率写作fset,则强耦合振子检测频率范围为0.34fset,非线性恢复力强耦合振子检测频率范围为1.25fset,双振子强耦合系统检测频率范围最广,为2.7fset.

由于混沌检测的原理本就具有频率相关性,其本质就是利用混沌振子对与系统内置频率相近的外来信号的高度敏感性,来检测该频率信号的有无,所以在系统内置频率设定后,混沌振子就只能检测一定频率范围内的信号,如果要检测不同频率下的信号,需要通过不断改变内置频率的方式来进行频率扫描.非线性恢复力强耦合振子和双振子强耦合系统相对于强耦合振子大大扩展了对脉冲信号的频率检测范围,这意味着在进行频率扫描时能更快寻找到最佳的信号检测频率.本文基于变迭代步长方法和混沌振子检测的频率相关性提出一种未知频率脉冲信号检测方法,首先通过变迭代步长的方法来代替系统内置频率变化,找到检测脉冲信号的较优等效输入频率,之后利用混沌检测的频率相关性,将系统恢复脉冲信号和接收脉冲信号的相关系数和纯噪声输入时的相关系数进行对比,判别接收信号中是否存在脉冲信号.变迭代步长的原理如图6 所示,混沌振子系统在检测信号时,系统的输入为一系列信号采样点,系统会对这一系列信号采样点进行解微分方程运算,此时进行求解的迭代步长默认视为信号采样率的倒数,增大运算时的迭代步长相当于增大信号的采样时间间隔,在信号采样率固定的情况下,即等效于系统的输入信号频率以同等倍数减小.由于系统内置频率改变会导致系统对脉冲信号的最佳检测参数发生变化,所以在进行频率扫描时,通过改变迭代步长的方法来代替改变系统内置频率,可以固定系统的内置频率及该频率下的最佳检测参数,避免参数对信号检测造成影响.

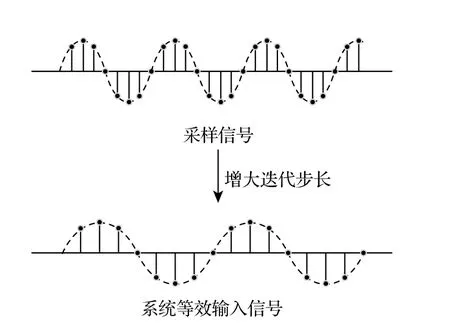
图6 变迭代步长原理图Fig.6.Schematic diagram of variable iteration step.

由于混沌振子检测具有频率相关性,系统只能响应一定频率内信号,其他频率的信号和噪声并不会对系统的输出造成影响,各个耦合系统对脉冲信号检测特性如图5 所示.通过变迭代步长得到较优的脉冲信号检测频率后,直接求接收信号和恢复信号的相关系数.如果接收信号中含有脉冲信号,那么脉冲信号作用于系统使系统发生突变,系统的恢复信号能保留脉冲信号特性,接收信号和恢复信号之间的相关系数会较大,而纯噪声情况下,由于振子对噪声具有一定的免疫特性,相关系数会较小,根据有无脉冲信号时相关系数的明显差异,可以判别接收信号中是否存在脉冲信号.系统检测脉冲信号的流程图如图7 所示,系统接收到信号Sn,设置内置频率f0和初始迭代步长h0.由于频率搜索跨度较大,对内置频率f0的要求并不高,为了避免错过最佳检测频率,f0可以设置一个较小的频率,初始迭代步长h0则根据信号采样率设置,为采样率的倒数.首先将接收信号Sn输入系统求系统的恢复信号,并求恢复信号和接收信号Sn的相关系数.由图5 可知耦合系统对脉冲信号的检测特性为,输入信号频率越低检测性能越好,所以在固定内置频率后,只需不断增大迭代步长,减小系统等效输入信号频率,就可以得到相关系数的最大值,即得到脉冲信号检测的最佳频率.之后将系统恢复信号再次输入系统进行降噪,并求此时系统输出和接收信号的相关系数,记为r.然后生成和接收信号能量一致的高斯噪声,并同样输入系统两次进行降噪,求系统输出和生成高斯噪声之间的相关系数,记为相关系数对比值ε,将ε乘一个误差保护系数η作为相关系数阈值,如果r大于相关系数阈值,说明两个相关系数之间存在明显差异,系统检测到脉冲信号存在,如果r小于相关系数阈值,说明此时接收信号对系统并没有造成影响,系统没有检测到脉冲信号.

图7 检测流程图Fig.7.Flow chart of detection.

4 仿真实验研究

4.1 微弱脉冲信号检测

为了验证所提脉冲信号检测方法的有效性,生成仿真三角脉冲信号,然后基于图7 流程进行检测,对比强耦合振子、非线性恢复力强耦合振子和双振子强耦合系统三者的检测率.设定系统内置频率为16 Hz,系统参数为默认参数,待测脉冲信号幅度为0.6,频率为10 kHz,即脉宽为0.1 ms,采样率1 MHz,采样持续时间为1 ms,信噪比为–20 到0 dB,误差保护系数取5,蒙特卡罗仿真次数为10000次,所得的三角脉冲检测率曲线如图8 所示.

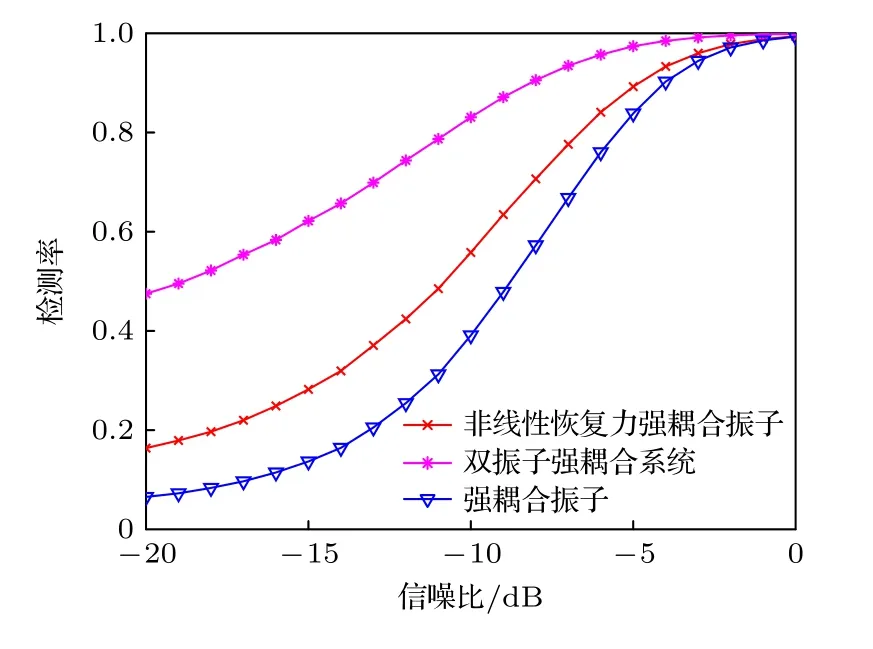
图8 耦合系统对三角脉冲信号检测率随信噪比变化曲线图Fig.8.Variation of detection rate of triangular pulse signal with signal-to-noise ratio by coupling systems.

由图8 可以看到,双振子强耦合系统检测性能最优,非线性恢复力强耦合振子次之,强耦合系统最差.在进行检测时,利用了混沌振子检测的频率相关性和噪声免疫特性,在输入噪声时进行了两次降噪来降低纯噪声输入时的相关系数,由于双振子强耦合系统引入了Van der Pol-Duffing 振子,Van der Pol-Duffing 振子具有优秀的抗干扰能力和检测灵敏度,所以能有效对噪声进行滤除并且在脉冲信号输入时有效恢复出脉冲信号,所以在检测时,有无信号输入相关系数差异较大,检测脉冲信号的检测率高.强耦合振子检测存在频率限制是因为强耦合振子在检测较高频率信号时会出现失真的情况,而这里为了降低噪声,在对接收信号进行波形恢复后还会再一次输入系统进行降噪,所以强耦合振子恢复的信号波形失真程度会进一步加大,所以恢复信号和接收信号的相关系数会偏低,在进行信号检测时检测率较低.非线性恢复力强耦合振子在强耦合振子的基础上引入了一个非线性恢复力耦合项,其作用是为了更好地保留信号中的高频分量,所以相对于强耦合振子,非线性恢复力强耦合振子恢复的信号失真程度会减弱,两者的相关系数会更高,所以在检测信号时检测率会比强耦合振子更高.图8 不仅验证了所提脉冲信号方法的有效性,而且进一步证明了所提改进结构的优越性.

4.2 瞬态脉冲信号检测

为了验证所提改进强耦合结构对瞬态脉冲信号的检测优越性,采用单指数衰减正弦脉冲来仿真瞬态脉冲信号,对比不同耦合结构对瞬态脉冲信号的检测率.仿真瞬态脉冲信号表达式如下:

其中,A为脉冲强度,τ为衰减常数,fc为震荡频率.仿真中取A=0.1,τ=10-6,fc=1 MHz,仿真噪声采用高斯白噪声,信号采样率取为10 MHz,瞬态脉冲信号以及加噪后瞬态脉冲信号如图9所示.

图9 瞬态脉冲信号及其加噪信号Fig.9.Transient pulse signal and its additive noise signal.

由图9 可以看到,瞬态脉冲信号脉宽极窄,无法进行波形恢复和相关系数求解,常用于检验振子对脉冲信号的检测性能,下面利用不同耦合结构对瞬态脉冲信号进行检测.设置系统内置角频率为106rad/s,仿真信噪比从–35 dB 到0 dB,对比弱耦合振子、强耦合振子、非线性恢复力强耦合振子和双振子强耦合系统对瞬态脉冲信号的检测率,检测率随信噪比变化曲线如图10 所示.

图10 耦合系统对瞬态脉冲信号检测率随信噪比变化曲线图Fig.10.Variation of the detection rate of transient pulse signal with signal-to-noise ratio by coupling systems.

由图10 可以看到,双振子强耦合系统检测性能最优,非线性恢复力强耦合振子次之,强耦合振子检测性能低于非线性恢复力强耦合振子,弱耦合振子性能最差.由于瞬态脉冲信号十分微弱,频率较高而且持续时间极短,所以瞬态脉冲信号相较于一般的脉冲而言,对强耦合振子产生的激励更为微弱,由信号激励产生的振子同步突变差异也较小,这也导致强耦合振子对微弱脉冲信号的检测性能有限.文献[16]中所提出的弱耦合振子并不能通过外来激励使振子发生反向突变,只能借助两个振子之间的失同步检测脉冲信号,检测性能要低于强耦合振子.非线性恢复力强耦合振子能通过非线性恢复力耦合项更好保留高频分量,在一定程度上提高了系统对瞬态脉冲信号的检测性能.改进强耦合振子是通过引入Van der Pol-Duffing 振子来提高系统整体的抗干扰能力和检测灵敏度,能更好识别到瞬态信号对同步振子产生的激励,从而提高了对瞬态信号的检测性能.图10 充分验证了所提改进强耦合结构对脉冲信号的检测优越性.

5 结论

本文提出了两种改进强耦合振子结构,分别为非线性恢复力强耦合振子和双振子强耦合系统.非线性恢复力强耦合振子通过引入非线性恢复力耦合项,更好地保留了信号的高频分量,双振子强耦合系统通过引入Van der Pol-Duffing 振子,提高了系统整体的抗干扰能力和检测灵敏度,可以更好地识别信号对同步振子产生的激励.两种改进强耦合振子结构通过不同的方式实现了脉冲信号检测频率范围的扩展,并提高了系统对瞬态脉冲信号的检测性能.同时,为了实现对未知频率脉冲信号的检测,本文基于变迭代步长方法和混沌检测的频率相关性,提出了一种未知频率脉冲信号检测方法,通过变迭代步长找到系统对脉冲信号检测的最佳频率,然后求输入信号和恢复信号的相关系数,和输入纯噪声情况下的相关系数做对比,可以准确检测出未知频率的脉冲信号.仿真结果表明所提检测方法和所提改进强耦合结构可以实现对脉冲信号的有效检测.