极坐标下基于圆的无人机纯方位无源定位研究

赵延阳，丁奕心，崔家铭

（辽宁工程技术大学 电气与控制工程学院，辽宁葫芦岛，125000）

0 引言

随着电子信息技术的更新迭代，探测定位技术在不断发展，同时探测定位技术在军事斗争中的地位和作用得到不断提高[1]。传统的有源探测定位会不断发射出电磁波，极易被对方侦查到，导致生存能力下降。相比于有源定位技术，无源探测定位技术具有很多优点，其中最重要的一点是本身不发射信号，因此不易被对方捕获自身的位置，使得自身生存能力大幅提升。因此无源定位技术得到越来越广泛地研究和应用[2]。本文针对无人机编队调整问题，通过纯方位无源定位方式对无人机进行调整，研究在极坐标下基于圆的无人机纯方位无源定位系统及其推广。

1 前提假设

假设在无偏差的情况下，9 架无人机均匀分布在圆周上，发射信号无人机的位置无偏差，因此发射信号无人机的排布满足正九边形的几何特征[3]。具体体现在：无偏差时，发射信号无人机之间的角度关系与距离关系是确定的，即图1 中虚线长度、发射无人机之间的圆心角可知。考虑发射信号无人机与接收信号无人机的位置我们可以发现，待定位无人机都是以与发射信号无人机之间的连线长度与夹角信息α1，α2，α3而确定圆的公共交点。编队由10 架无人机组成，形成圆形编队，其中9 架无人机（编号FY01 ～FY09）均匀分布在某一圆周上，另1 架无人机（编号FY00）位于圆心(见图2)。无人机基于自身感知的高度信息，均保持在同一个高度上飞行。选择三架无人机发射位置信号，已知发射信号的无人机位置无偏差[4]。

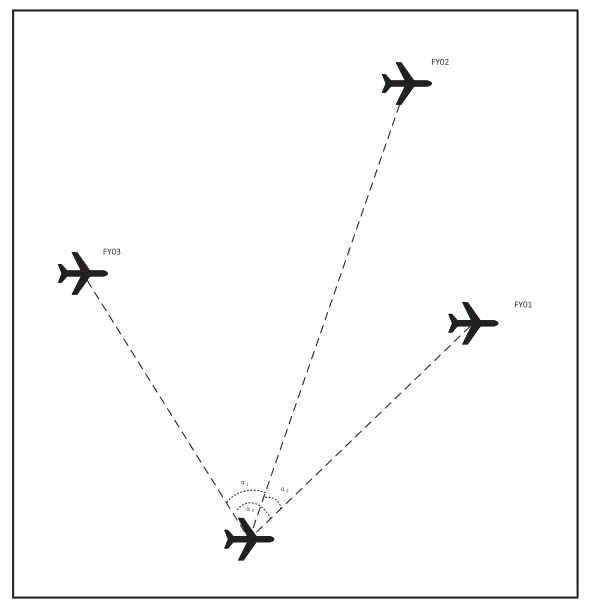
图1 无人机纯方位无源定位原理示意图

图2 无人机编队组成示意图

2 纯方位无源定位模型建立

这一节在无人机FY00和另2架编号已知的无人机发射信号且位置皆无偏差，其余位置有偏差的无人机接收信号的情况下，建立接收信号的无人机的定位模型。

■2.1 极坐标系的建立

已知发射信号无人机的编号，将FY00 无人机记为坐标原点，其与FY01 所在直线为极轴建立极坐标系。另一已知发射信号的无人机坐标为FY0F(R,γ)(2≤F≤9)(见图3)设接受信号无人机FY0X的理想极坐标为。

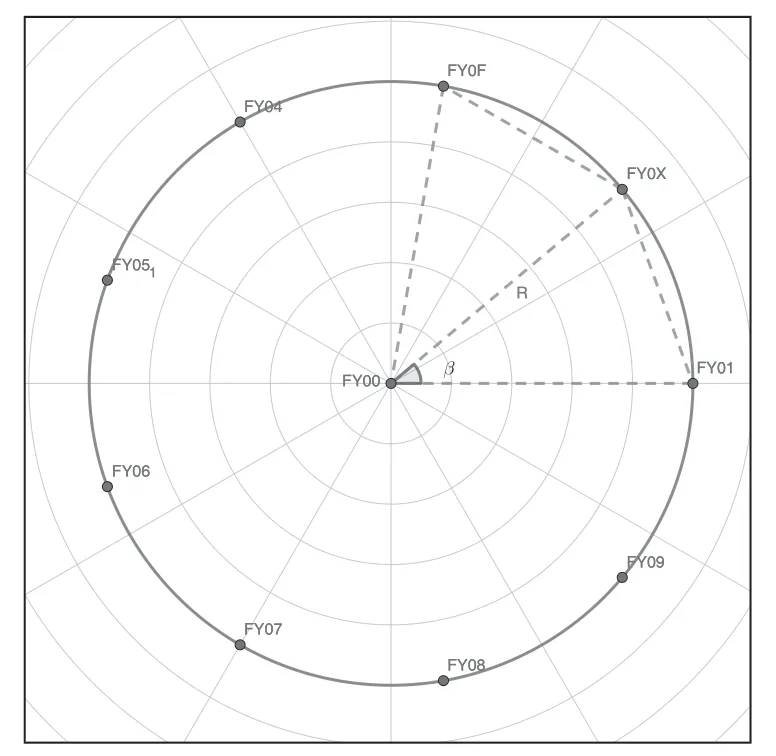
图3 极坐标下无人机编队示意图

■2.2 无人机定位模型的建立

过FY00，FY01 ,FY0F三点作圆，令FY00，FY01，FY0F分别为A、B、C，无人机定位模型由发射信号无人机进行分析计算，将理想位置的信息发送给临近理想位置的接收信号无人机，无人机在接收信号后将在自身调整至理想位置。讨论发射信号无人机的位置被定位无人机位置之间的关系：如图4 所示，已知α1+α2=α3，AB=AC，θ=∠BAC，通过三角形正余弦定理可得：

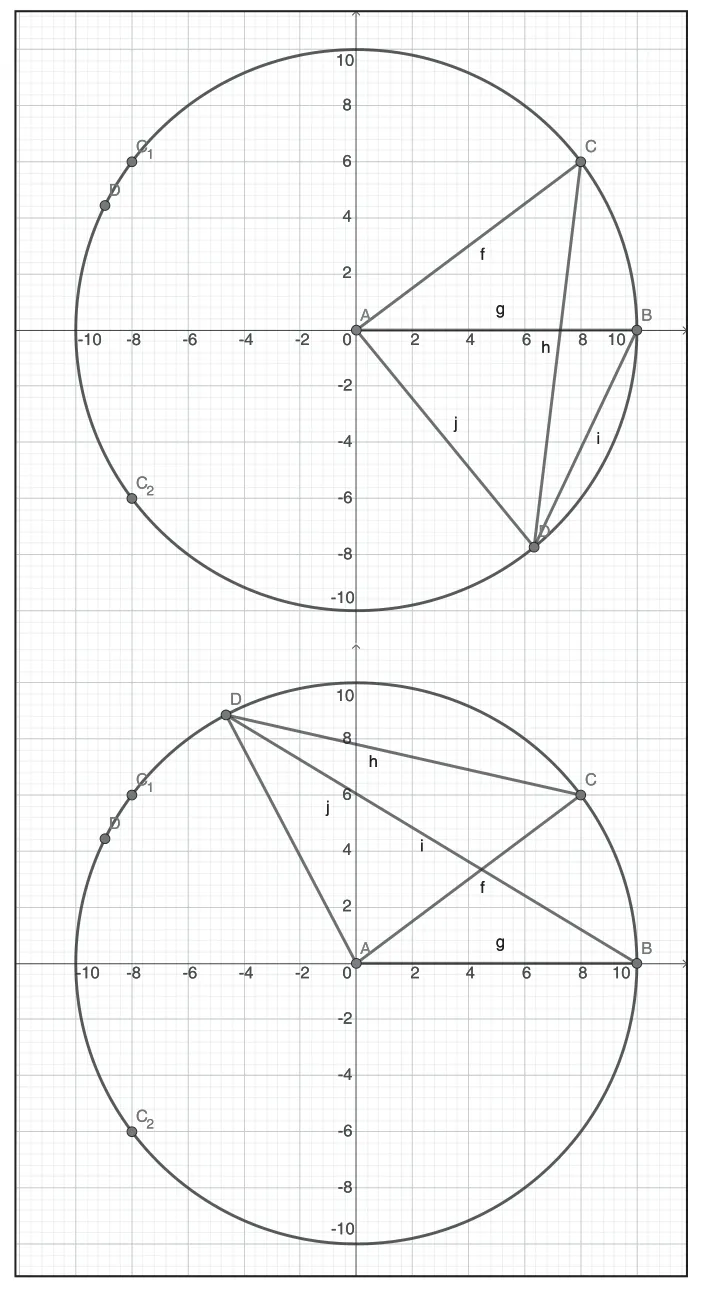
图4 根据D 点不同时编队的临时几何特征

2≤X≤5 时，有α3＜π：

5≤X≤9 时，有α3＞π：

解得接受信号无人机FY0X的理想极坐标为D(R,β)：

所以接受信号无人机FY0X的具体位置信息为(R1,β1)，可得无人机移动距离为：

3 无人机数量的最小化

无人机在编队飞行时为避免外界干扰，应尽可能保持电磁静默，减少向外发射电磁信号，所以要保证准确性的前提下尽可能减少无人机向外发射电磁信号的频率及发射源的数量[5]。

通过选用三角定位算法，设FY00-FY09九架无人机的编号为0，P1-P9。取圆上任意两个无人机Pn1,Pn2为发射源，设圆周半径为R，Pn1(Rcosθ1,Rsinθ1)，Pn2(RcosC,Rsin θ2)，我们通过三角定位算法可以确定接收信号无人机D(x,y)的θ1表达式、θ2表达式、同时含有θ1和θ2表达式。联立三个表达式我们可以消除θ1和θ2，给出四架无人机信号源的分类方式如表1 所示。

表1

已知O( 0,0 )P1(R,0)，根据以上分类开始使用三角定位算法计算目标点坐标：首先根据分组，得出三个圆的方程，求得圆心坐标和半径。对于分组一、二，根据O1P还有D与O1P夹角1α，可以唯一的确定一个圆，设其圆心为O1(x1,y1)，半径为r1，可得：

从而求解出O1(x1,y1)与r1，解得：

对于分组三、四：

解得：

得到x1～x4四个点坐标和四个半径后，因为已知方程组：

任取其中三个，一共有四种组合。由于D 点是其中任意三个圆的唯一交点，因此可以确定，本模型不需要进行估算，所以可以直接通过解上述方程组消去未知数θ1,θ2，从而求得从而求得D坐标(x,y)，实现了有效定位。

4 模型调整

已知接收信号无人机位置信息，建立调整模型，使无人机群在多次调整后均匀分布于某个圆周上。

■4.1 调整模型的建立

设计一种无人机编队位置调整方法，使在已知三架无人机位置信息后即可得出其余无人机位置。具体流程图如图5 所示。

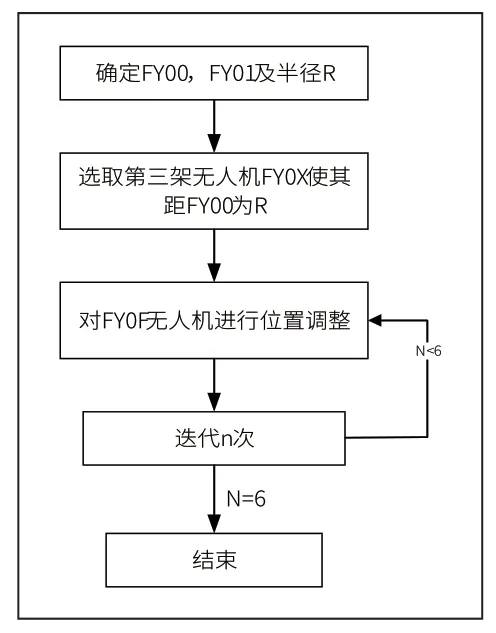
图5 无人机位置调整流程图

■4.2 调整模型的求解结果

根据初始坐标计算出无人机接收到的方向信息α1,α2，接着按照上述两种方法的步骤分别进行2 次迭代（取R＝100m）。最终得到无人机组完成迭代前后的坐标对比如表2 所示。

表2 无人机计算前后的坐标

可见该方法在无人机编队调整中系统误差较小，具有良好的准确性。

5 总结

本篇论文中，大部分过程都严格使用数学化的表达方式，使无人机位置定位更加严格，具有解析性，模型准确度更高。无源定位可以不依赖问题信息，可以拓展至多个无人机系统中，能够实现无人机协同搜索，同时利用个体局部信息和群体全局信息进行局部搜索。达到目标最优解的速度快，对计算机处理器和内存要求不高。将复杂问题转化成单一问题重复操作，简化解体步骤，效率高。