混合课程对物流管理专业学生绩点的影响因素分析
杨雪陶,张荣祯
(南京邮电大学,江苏 南京 210023)
0 引言
南京邮电大学于2016 年10 月成立现代邮政学院,其物流管理专业面向现代邮政信息和邮政物流快递服务,与国家邮政局及邮政、快递及物流企业等开展政产学研合作,越来越受到大众的青睐。该专业主要培养适应现代物流服务业发展需要,具有较高的思想道德和文化修养,具有国际视野、创新精神和实践能力的物流管理专业人才。物流管理专业的学生需要掌握管理科学基础理论、现代物流管理理念等专业知识,能够熟练运用现代物流与供应链管理理论、系统规划设计方法、计算机信息技术[1-2]。但是从该专业学生的课堂表现与考试成绩来看,传统课堂主要存在如下几个问题:(1)学生的基础不同,教师无法实现个性化教学;(2)专业课程较为枯燥且教师为主学生为辅的教学模式很难调动学生学习的积极性;(3)传统教学受时间空间限制很大。
随着“互联网+”时代的到来,学习场景地点发生了巨大的变化,学习不再被拘于小小的教室之中,传统课堂教学与在线学习相结合的混合式教学模式应运而生。相对于传统教学的不足,混合教学能够以学生为主体,实现精确、个性化教学,构建高校互动教学模式,实现精准学习评价。且通过线上教学和线下教学的有机结合,可以充分实现学习环境、学习资源和学习方式的合理整合,不受时间空间的限制。建设线上、线下混合教学课堂,能够更好地践行以学生为主体的新时代教育思想,提高教学质量,促使学生深度学习,满足当代大学生发展实际需要,培养走向新时代的人才。目前,国内外已有众多针对“互联网+”混合教学的相关研究[3-9],例如:王晶心等[3-4]运用相关分析和多元线性回归分析等方法研究基于MOOC 的混合式课程对北京大学在校生的学习影响;许德泓[5]通过案例分析法和对比分析法,纵向跟踪福州大学在2007—2016 年期间实施混合教学改革的效果;徐凤等[6]以《运筹学》课程为例,阐述了混合教学模式的设计。
然而现有研究大多没有采用定量的研究方式,缺乏数据分析的理论支撑且研究手段较为单一。因此,本文采用物流管理专业学生总平均学分绩点(GPA)为因变量,基于线上发布并收集的310 份调查问卷的数据,运用描述性统计、交叉分析、有序logistic 回归分析等定量研究方法来研究混合课程对该专业学生绩点的影响。
1 交叉分析结果
本次调查面向南京邮电大学现代邮政学院物流管理专业本科全日制大学生随机发放问卷。调查问卷采用问卷星设计,并发布线上问卷。问卷主要内容包括学生个人情况(性别、年级、专业、日平均学习时长、GPA 等)以及物流管理专业学生对学校混合课程设计的态度、了解程度、满意程度和适应程度等,共计设置22 个问题。一共发放350 份问卷,收回有效数据310 份。利用SPSS 分别以学生个人情况和混合课程开展情况两个方面进行学生的GPA 交叉分析。
1.1 个人情况与GPA 的交叉分析
根据表1,使用卡方检验,做如下假设:
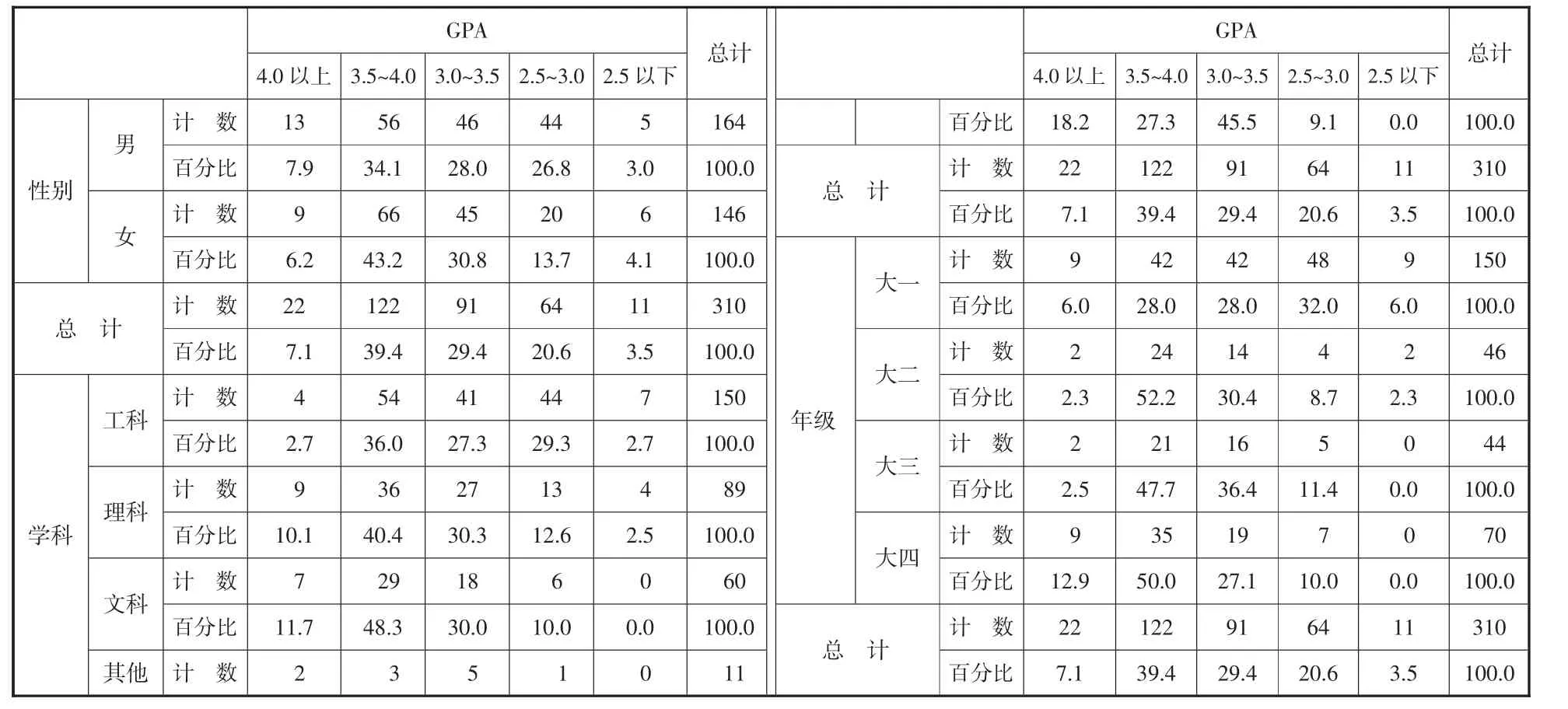
表1 个人情况与GPA 之间的交叉表
(1)H0: 性别和GPA 之间是独立的;VS H1: 两者之间不独立。
(2)H0: 学科和GPA 之间是独立的;VS H1: 两者之间不独立。
(3)H0: 年级和GPA 之间是独立的;VS H1: 两者之间不独立。
由表2 可知,性别、学科类型、年级和GPA 之间的卡方检验的P 值均小于0.05,拒绝原假设,表明性别、学科类型、年级和GPA 之间不独立,存在一定相关性。

表2 卡方检验P 值表
由表3 可知,性别、学科类型、年级和GPA 之间的列联系数c,Cramer's V,近似显著性表明性别、学科类型、年级和GPA 之间存在一定的关联程度。

表3 相关系数表
1.2 混合课程开展情况与GPA 的交叉分析
(1)了解程度、适应速度和日平均学习时长分别与GPA 的交叉分析结果如表4 所示。
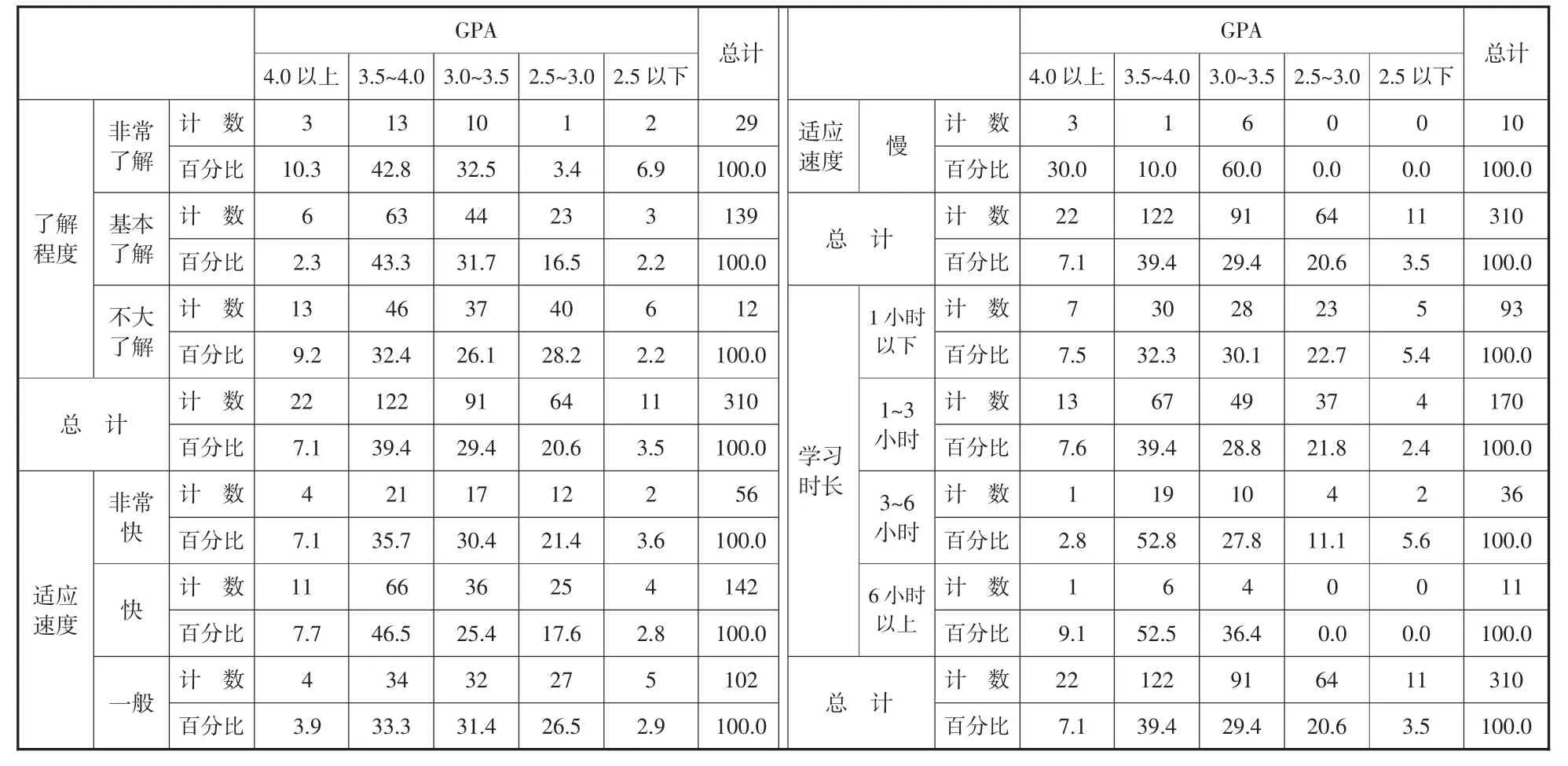
表4 混合课程开展情况与GPA 之间的交叉表
类似1.1 节使用卡方检验以及相关系数分析,得到结论:对混合课程的了解程度、适应速度和GPA 之间存在一定的关联程度,但混合课程日平均学习时长和GPA 之间不存在关联。
(2)作业完成情况、专注程度和讨论情况分别与GPA 的交叉分析结果如表5 所示。
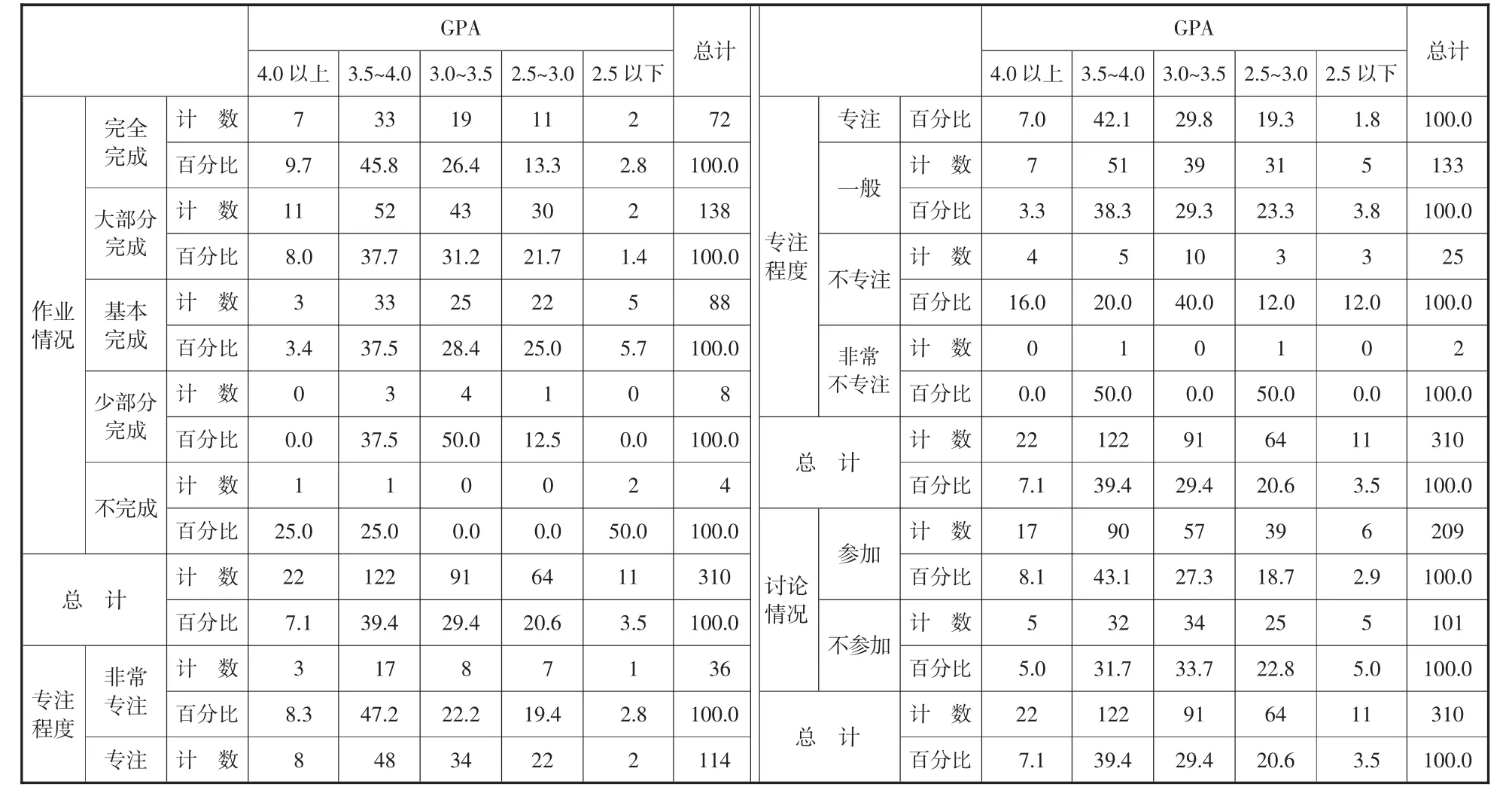
表5 混合课程开展情况与GPA 之间的交叉表
同样地,使用卡方检验及相关系数分析,可知,线上学习作业的完成情况和GPA 之间存在一定的关联程度,而线上学习的专注程度、讨论情况和GPA 之间不存在关联。
2 有序logistic 回归分析结果
2.1 多重共线性检验结果分析
根据交叉分析结果,选取和GPA 之间存在一定关联程度的自变量:性别、学科类型、年级、对混合课程的了解程度、对混合课程的适应速度和线上学习作业完成情况,对其进行多重共线性检验,结果如表6 所示。
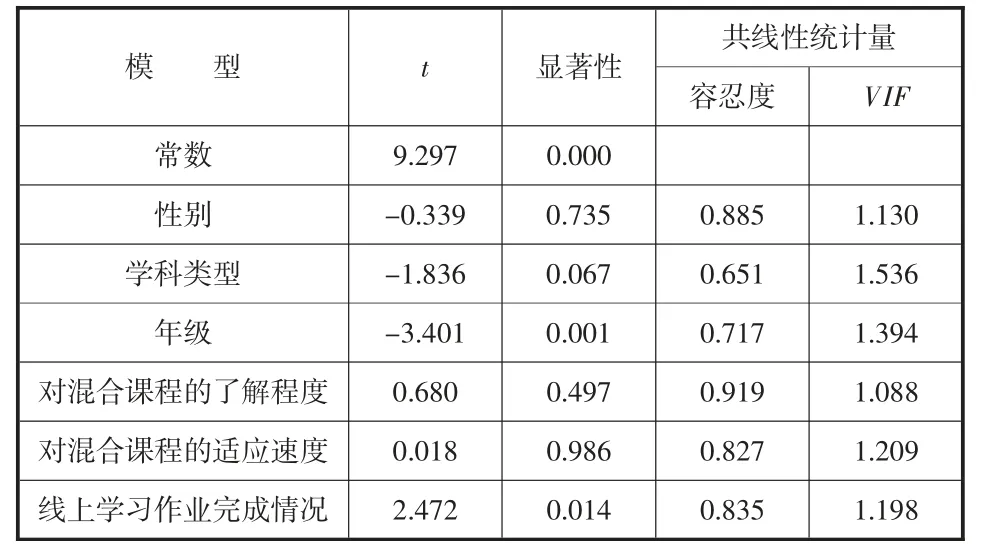
表6 多重共线性检验表
由表6 可知,容忍度均远大于0.1,方差膨胀因子VIF 均小于10,可认为自变量之间不存在严重的多重共线性。
2.2 平行线检验结果分析
根据表7,选择联系函数Complementary log-log,结果如表8 所示。

表7 联系函数表
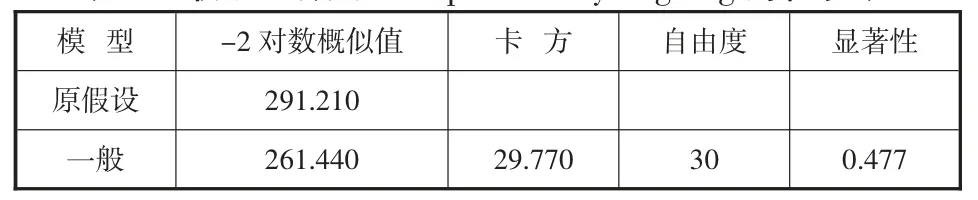
表8 联系函数为Complementary log-log 的检验表
当联系函数为Complementary log-log 时,显著性为0.477,大于0.05,不拒绝原假设,即认为满足平行线假设。
2.3 有序logistic 回归结果分析
有序logistic 回归结果如表9 所示。
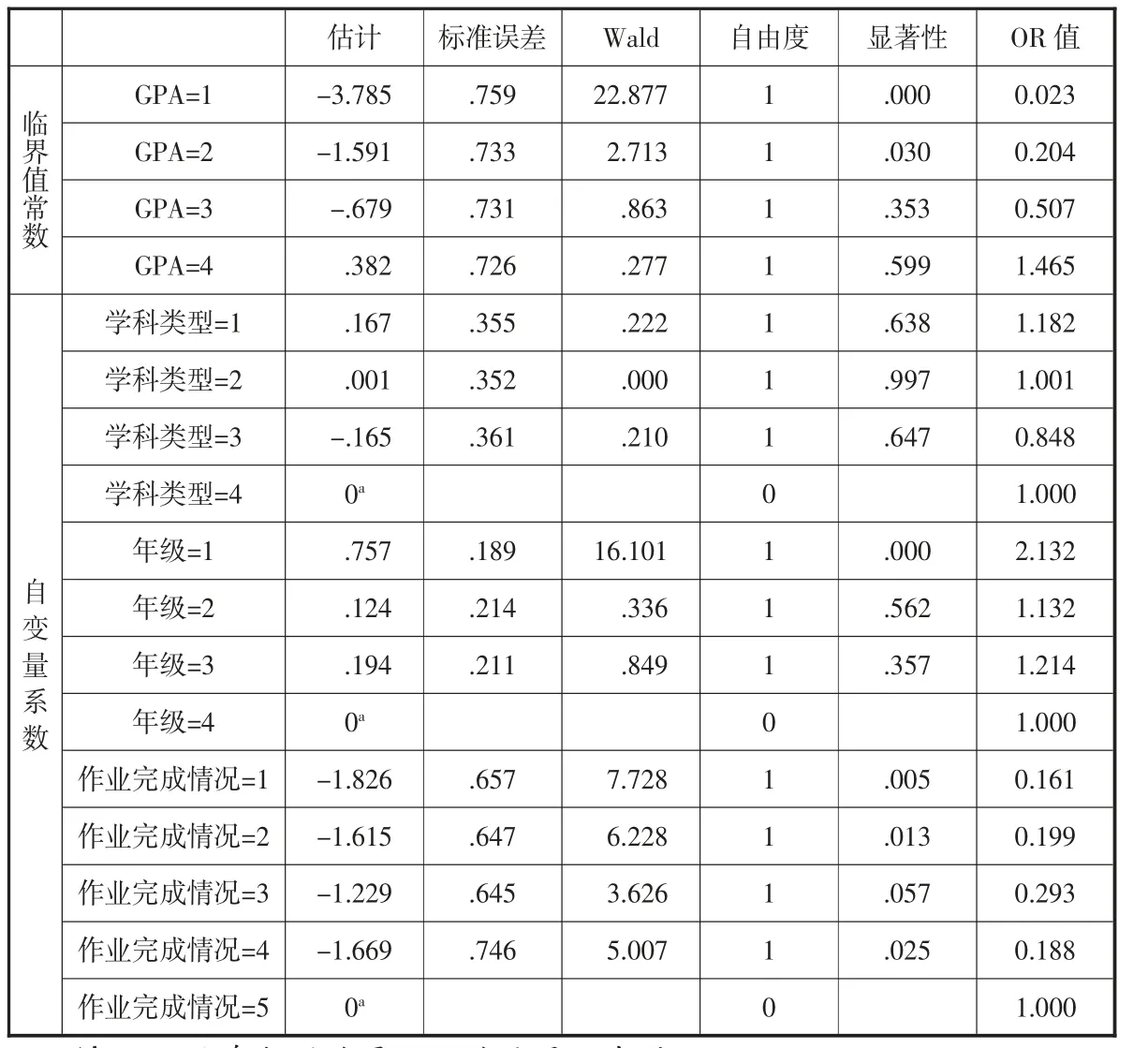
表9 参数估计表
表9 中,临界值常数GPA=1、GPA=2、GPA=3 和GPA=4 对应的估计值分别代表“4.0 以上vs4.0 以下”、“3.5 以上vs3.5 以下”、“3.0 以上vs3.0 以下”和“2.5 以上vs2.5 以下”的二元logistic 回归的常数项。自变量系数中,学科类型=1、2、3、4 对应的估计值分别代表“学科类型为工科”、“学科类型为理科”、“学科类型为文科”和“学科类型为其他”的自变量系数估计值;年级=1、2、3、4 对应的估计值分别代表“年级为大一”、“年级为大二”、“年级为大三”和“年级为大四”的自变量系数估计值;作业完成情况=1、2、3、4、5 对应的估计值分别代表“作业全部完成”、“作业大部分完成”、“作业基本完成”“作业少部分完成”和“不完成”的自变量系数估计值。
由表9 可以看出,在显著性水平为0.05 时,学科类型不会对GPA 等级水平产生显著影响。而“年级=2”、“年级=3”及“作业完成情况=3”也均未在模型中呈现显著性。
2.4 有序logistic 回归模型检验
对模型中是否所有自变量偏回归系数全为0 进行似然比检验,由表10 可知,显著性0.000 小于0.05,说明至少有一个自变量的偏回归系数不为0,即拟合包含学科类型、年级和作业完成情况3 个自变量的模型拟合优度好于仅包含常数项的模型。

表10 模型拟合信息表
3 结论与混合课程改进措施
3.1 结论
通过对物流管理专业学生个人基本情况、混合课程开展情况同GPA 的交叉分析以及以GPA 为因变量的有序logistic 回归分析可得以下结论:
(1)年级对GPA 具有显著影响,且年级为大一的学生更为明显,相对于其他年级的学生,其GPA 处于较低等级水平的概率更高。性别、学科类型和GPA 之间虽然存在一定的关联程度,但对GPA 的影响并不显著。
(2)混合课程线上学习作业完成情况对GPA 具有显著性影响,而且作业完成情况越好,GPA 所处等级水平的概率也相对越高。对混合课程的了解程度、对混合课程的适应速度同样和GPA 之间存在有一定的关联程度,但对GPA 的影响并不显著。
3.2 改进措施
(1)学院应积极发挥顶层设计的作用,高屋建瓴,确保物流管理专业学生,尤其是大一新生充分了解混合课程的形式、内容等,加快其对混合课程的适应速度,进而达到大力提升混合课程具体内容的开展。
(2)教师应提供课程的电子课件、在线资源、精品课程等,丰富学习内容。从图1 可以看出,需加强学习监督力度。比如:每次线上课程中设置签到环节,计入课程总成绩的计算,线上课程打开视频,突击检查,采用实时互动的直播问答等方式。从图2 和3 可以看出,教师可以开展线上线下课程的有机结合,丰富课程内容,使用生动的视频语言、在线资源,以弹幕留言的方式与学生互动,调动学生的积极性。
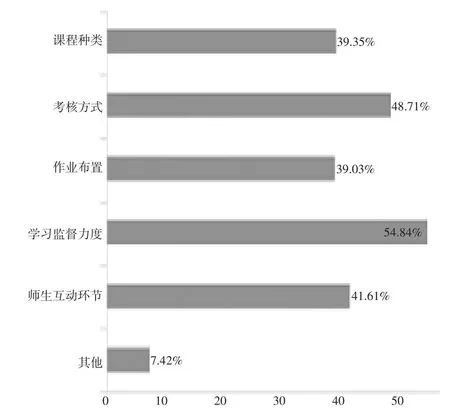
图1 学生对混合课程的改进看法
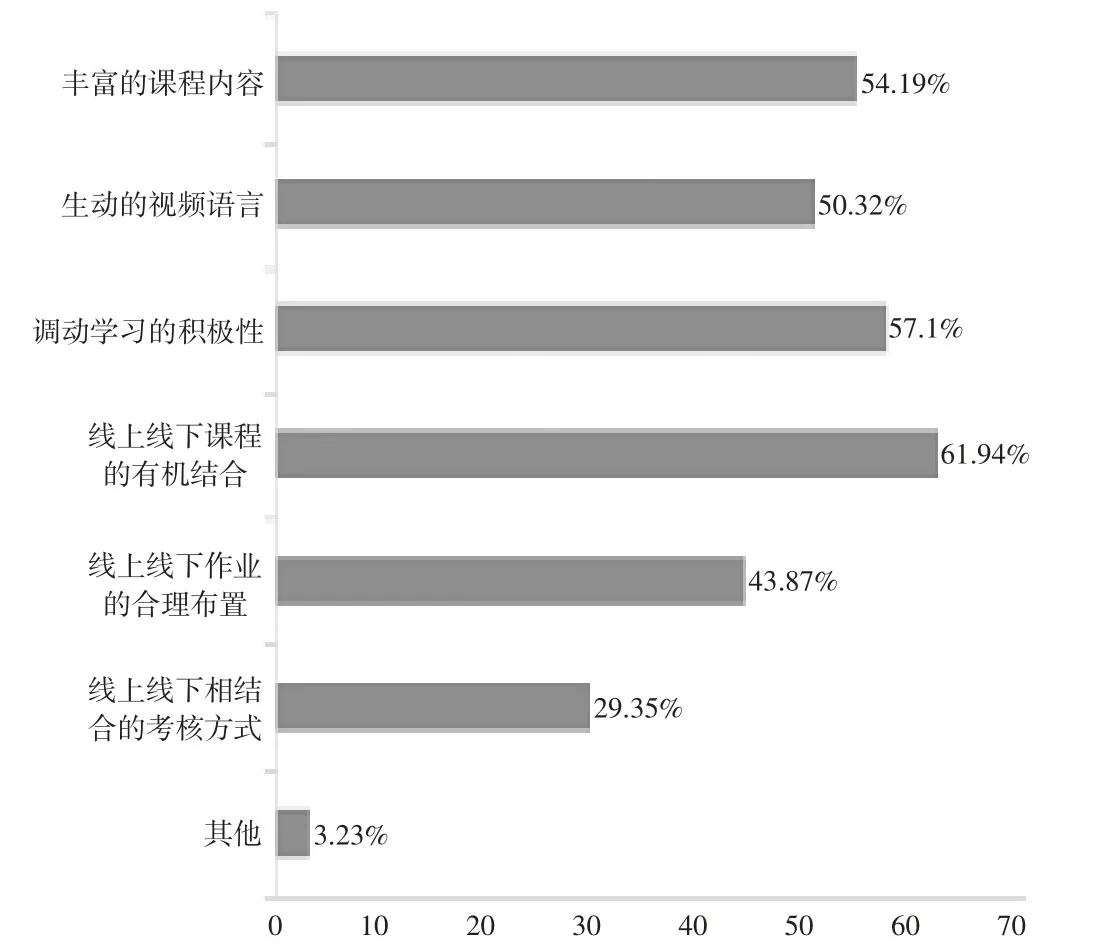
图2 学生对混合课程核心的看法
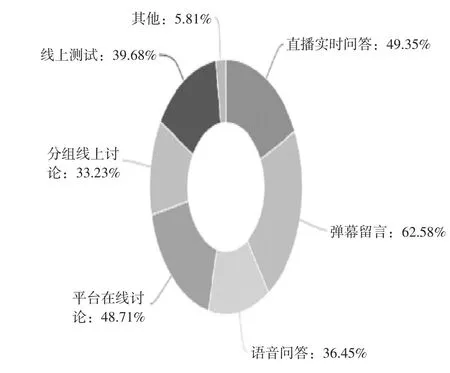
图3 线上学习方式图
(3)从图4 以及有序logistic 回归分析可以看出,物流管理专业学生应提高自制力,以高效率积极投入到线上线下的课堂中而不是长时间却低效率的学习,尤其是作业完成情况,应独立按时完成作业、多与教师交流,在平时就打下坚实知识基础。
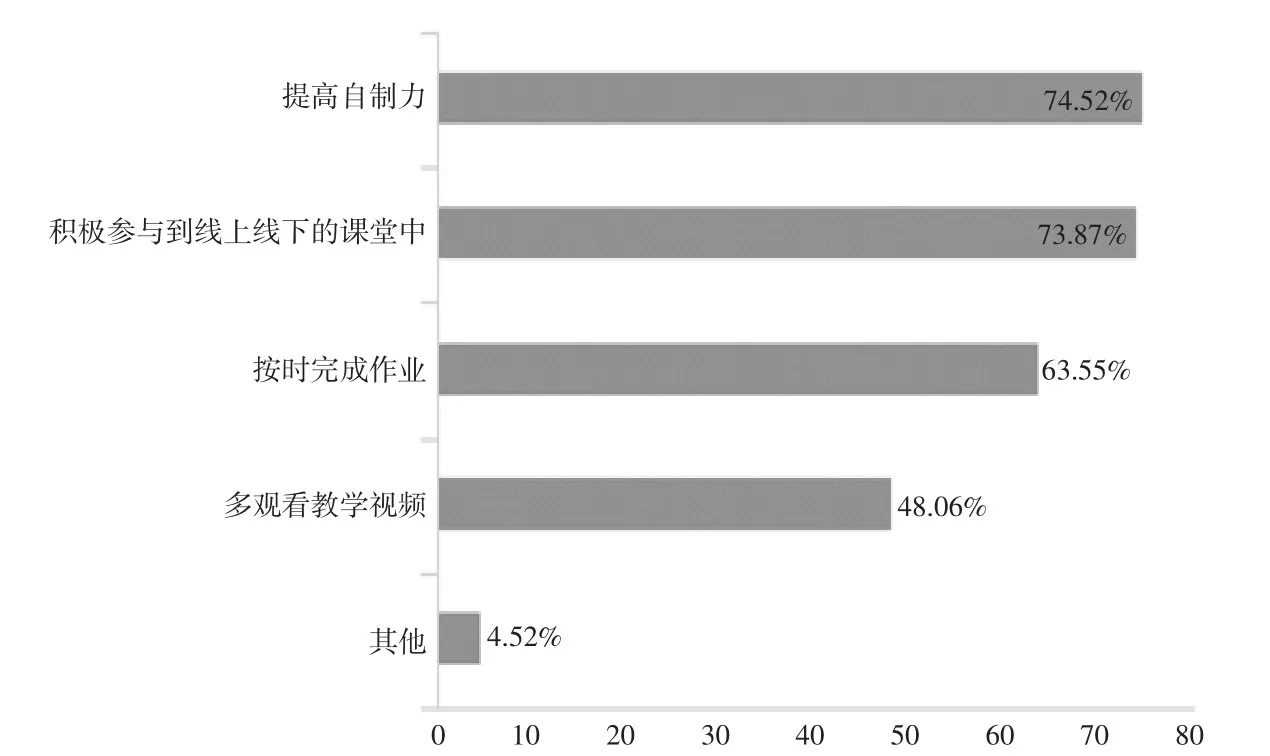
图4 适应混合课程具体做法图

