基于混合遗传算法的堆垛机路径优化研究
蒋小燕,周先烨
(重庆交通大学 机电与车辆工程学院,重庆 400074)
0 引言
随着物流行业的迅速发展,仓库货物的存储逐渐变得智能化,在不断优化的仓储系统中,堆垛机作为连接货物和货架的纽带[1],一直是不可或缺的存在,堆垛机的行走路径对货物的存取效率有较大影响,提高运送效率能够提高立体库的整体运作效率,降低公司成本。
优秀的路径规划能够提高堆垛机系统的工作效能。华祎明等[2]利用遗传算法研究了堆垛机的作业形式对立体库工作效率的影响,构建了多目标优化模型。蔡安江等[3]利用遗传算法研究和解决了堆垛机的调度问题。闫青等[4]利用遗传算法将集束搜索作为初始路径,有效避免了算法陷入局部最优解。因此,对效率要求高的立体仓库货物存储系统,普遍存在货架的布局没有达到最优化、堆垛机的路线杂乱、WCS 控制系统的算法落后等问题[5]。这些问题都会对堆垛机的运行效率带来巨大的影响,针对上述问题,提出了新的混合遗传算法,以此来优化堆垛机路径,从而提高整个立体仓库的工作效率。
1 堆垛机的路径优化数学模型
1.1 仓库整体布局设计
通过立体仓库货架的巷道数量以及堆垛机的数量来确定所需堆垛机的数量,立体仓库的模型参数设置为:库位层数12 层、巷道数目4 条、库位列数50 列、每个库位长度2 米、每个库位高度为1.8 米,利用已知的仓库参数条件进行立体仓库的整体布局图设计如图1(a)所示,就单个的仓库货架俯视图,将堆垛机的运行区域划分成3 个,A 区表示传送区、B 区表示存取区、C 区表示暂存区,如图1(b)所示,由于堆垛机是在直线巷道中工作,因此为了方便对堆垛机的行走路径进行简化可视,将其视为竖直的二维格子地图。

图1 仓库整体设计
1.2 堆垛机路径优化数学模型
立体仓库的运行从数学上可以描述为有n 个待取的货物要在m 个货架上进行逐个存取,设立体仓库中有N 台堆垛机,有S个输入库任务,堆垛机的载重量为Q,每单个任务的重量qn(n=1,2,3…,m),需要向M 个货架库位送货,及货架的库位编号为m(m=1,2,…,M),将S/N=P(令P 为整数)个作业批次,且每个批次的任务总重量小于或等于堆垛机的载重量,一个作业批次,堆垛机进行逐个入库处理,可建立如下的堆垛机行走路径数学模型[6]:
其中:式(1)为总体运行的目标函数,Dmin为堆垛机完成一个任务批次所行走的最短距离,库位i 到库位j 的运距为dij,货台到各库位的距离为d0i(i、j=1,2,…,m),设D01=0 表示第一个存货库位到取货台的距离,D0M表示最后一个存货库位到取货台的距离。式(2)为重量的约束条件,设常数Q=30kg。
2 堆垛机路径优化的混合遗传算法
2.1 蚁群算法简介
利用蚁群算法解决路径优化问题的过程可以概括为:蚂蚁能够走通的路线表示优化问题中的可行解,那么蚂蚁在多个点上形成的所有不同路线,就代表了路径优化中的所有解,最优解就会在这些解空间中产生[7]。蚂蚁在路径选择点上会留下信息素,通过不同的路径尝试,蚂蚁会在最短的路径点上留下较强的信息素,随着不断的累积,最短路径上的信息素沉淀总和最多[8]。在正反馈机制下,蚂蚁群体会自然而然的集中到最优路径上,此时的路线就是优化过程中的最优解[9]。
2.2 遗传算法简介
遗传算法是一种进化算法,其主要思想是模仿生物界的“物竞天择”的进化法则[10]。通过编码、选择、交叉以及变异等操作,获得优化后的最优染色体。遗传算法在全局搜索上的能力较强,而在局部搜索上就相对薄弱,因此,在搜索最优解的过程中,遗传算法所耗费的时间较多[11]。
2.3 混合遗传算法
结合蚁群算法和遗传算法的优点,形成新的混合遗传算法,该算法可改进遗传算法在局部搜索能力上的不足,算法通过遗传算法的一系列操作后,通过蚁群寻优操作进行交叉处理得到的个体会取代原个体,以增强算法的局部搜索能力[12]。新的混合遗传算法以遗传算法为主体,在局部程序上加入蚁群算法。混合遗传算法的优化如下[13]:
(1)编码的设计
对货架进行整数编码排序,将存取货架视为染色体,将染色体等分成货架数量一致的切割段,其中不同段位对应不同的货架编号[14]。
(2)种群初始化
对染色体的编码设计完成之后,初始种群会产生初始解,通过货架的容量及大小来决定初始种群的数量[15],实验中取得种群数量为80。
(3)适应度函数
(4)选择操作
适应度值可以决定选择操作中,在旧群体中被选择的个体会被放入到新的种群里去,适应度值高的个体被选择的概率也大[7]。
(5)交叉操作
利用顺序局部交叉的方法,先确定两条父代染色体交叉部分的左右两个位置,假设为第5 段和第8 段,将5 和8 段之间的两组节段进行交叉组位,如:灰色部分进行交叉为:
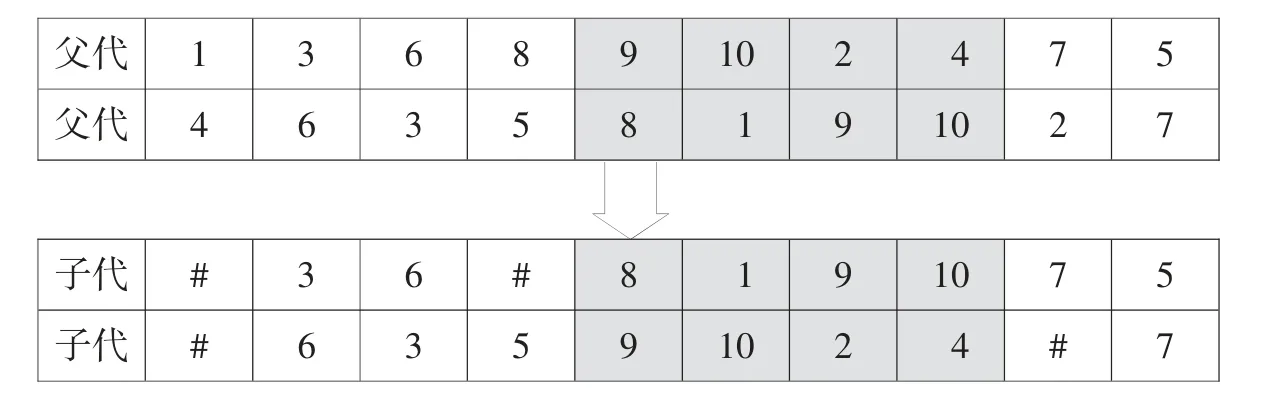
交叉后,同一条染色体中有重复的货架编号,保留出现不重复的数字,重复的部分会利用映射关系进行数字填充,填充后的结果为:

(6)变异操作
变异操作在同一条染色体重新完成,采用两两对换的方式,例如将第5 段与第8 段的编号进行交换,得到新的子代染色体如下:

(7)蚁群优化操作
遗传算法在局部搜索能力上存在很大的不足,在编码、选择、交叉、变异之后,引入蚁群算法进行寻优操作,即只保留信息素所增加的操作,否则忽略。蚂蚁在不同点位之间移动就会构造出一个解,那么形成这个解的概率可用以下公式(4)表示[17]:
式中:τij表示蚂蚁走过每条路线所留下的信息素;ηij表示验证ij 路线的可取性,一般为ij 两个库位之间距离的倒数;α 表示控制τij的参数,需满足大于或等于0 的条件;β 表示控制ηij的参数,需满足大于或等于1 的条件;τiz和ηiz表示所有可能的解。
全局信息素的更新规则如式(5)、式(6)所示:
式中:τij表示蚂蚁走过每条路线所留下的信息素总量;表示第k 只蚂蚁所产生的信息素总量;ρ 表示蚂蚁的信息素的挥发系数;S 表示蚂蚁的数量;Q 表示信息素总量;Lk表示第k 只蚂蚁行走的路程。
(8)结束操作
通过信息素浓度的高低来对每个个体进行交叉变异,利用适应度值的大小对其进行好坏评估,信息素浓度较好的会进入下一次的交叉、变异和逆转操作,判断操作是否循环的依据是:遗传代数以及信息素浓度的大小是否达到最优[18]。不满足条件就会转入适应度值的计算,否则,结束遗传循环操作。
3 结果分析
利用案例来完成算法优化的验证试验,通过已知条件将信息绘制成表格,如表1 所示:
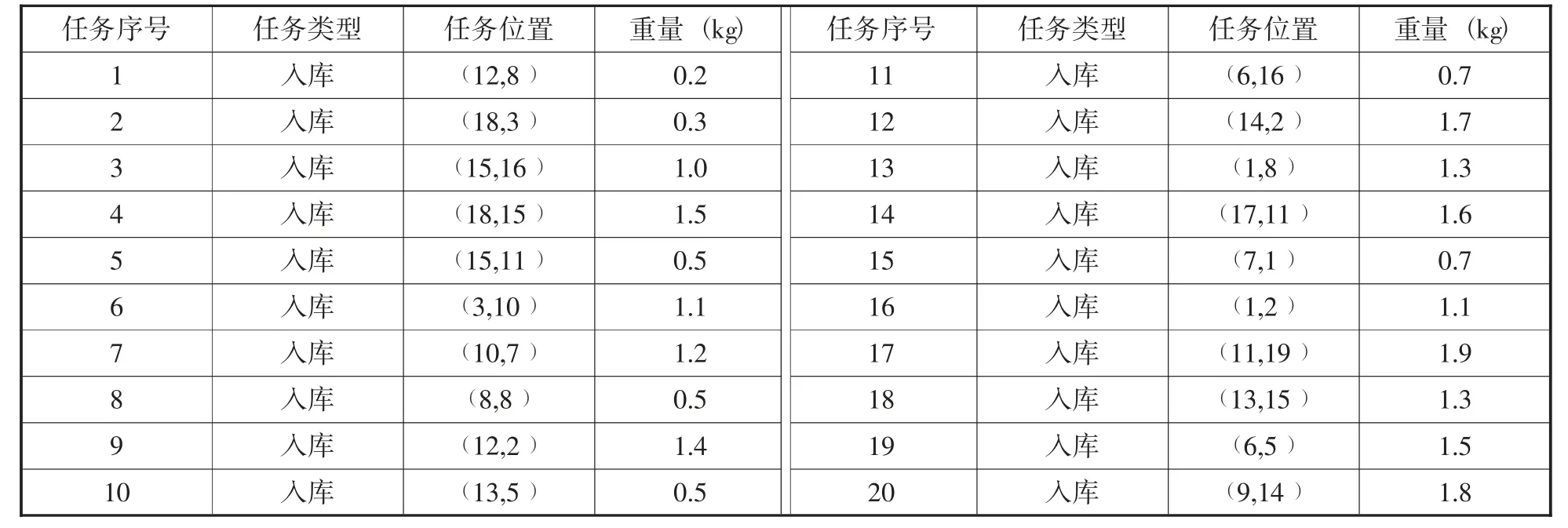
表1 入库信息表
在利用两个算法进行对比实验时,保证各个参数不变且相同,因此设置的算法参数如表2 所示。

表2 算法参数表
混合遗传算法在10 次搜索中的最优解为96.3km,如表3 所示,相对于单纯的遗传算法,其余解与最优解也较为接近,其最优解对应的路线轨迹为:20→11→6→13→15→19→8→1→7→10→9→12→2→14→5→4→3→17→18。

表3 混合遗传算法的搜索结果
遗传算法10 次搜索中的最优解为99.5km,如表4 所示,对应的路线轨迹为:18→1→17→11→20→7→10→13→6→8→19→16→15→12→9→2→5→14→4→3。

表4 遗传算法的搜索结果
实验分析:混合遗传算法和遗传算法进行比较分析,分别对两种算法进行10 次搜索,对其每项平均值进行对比,如表5 所示。

表5 两种算法对比分析
4 结论
通过建立自动化立体仓库的基础模型,对堆垛机在传统路径选择中使用到的遗传算法进行了优化,形成新的混合遗传算法,有效地解决了遗传算法在局部搜索能力上的不足,使得堆垛机在拣选货物的过程中行走的路径最优,该算法对提高堆垛机运行效率提升上有显著成效。不足之处,当订单出现较多出库和入库要求时,堆垛机会出现呆滞问题。

