基于动态调节下垂曲线的光伏逆变器两阶段协调控制策略

王键，钱瞳，唐文虎，吴承虎，陈嘉伟，申悦晴，龚贤夫

(1.华南理工大学 电力学院，广东 广州 510641；2.广东电网有限责任公司电网规划研究中心，广东 广州 510080)

近年来，在“双碳”目标的推动下，我国分布式光伏装机总容量迅猛攀升，2022年，分布式光伏新增装机51.1 GW，同比增长高达74.5%[1-2]。分布式光伏渗透率持续升高，也给配电网的运营带来了一系列重大的技术挑战，例如潮流倒送导致的电压越限问题[3]和光伏快速变化导致的电压波动问题[4]。相比于有载调压变压器[5]和并联电容器[6]等常规调压设备，光伏逆变器具有响应迅速、可频繁控制和可独立调节有功/无功的优势[7-8]；因此，配电系统运营商(distribution system operator，DSO)应当采用更加有效的光伏逆变器电压控制策略，在经济效益和运营风险之间取得所需平衡[9]。

目前，主流光伏逆变器电压控制方式分为集中控制、局部控制两类。集中控制通常基于最优潮流(optimal power flow，OPF)优化算法实现[10]，需要DSO与各光伏逆变器建立高可靠、低延时的通信线路，这在当前大部分配电网中难以实现[11]，因而集中控制在抑制电压实时波动方面效果较差。局部控制通常只依赖于局部信息，依据一定的控制方式进行光伏逆变器的电压控制[12]，可以有效应对外部环境变化导致的电压快速波动问题。IEEE 1547-2018标准中提出的标准无功-电压(以下记为“Q-V”)下垂曲线是目前普遍采用的局部电压控制方式[13-14]；然而，局部控制无法根据不同运行场景动态调节下垂控制曲线，来实现全局最优的电压控制效果。

为了解决集中控制、局部控制无法兼顾电压控制实时性、最优性的问题，考虑到目前配电网具有一定的通信能力[15]，国内外学者提出了集中与局部相结合的电压控制方式。文献[16]以最大消纳可再生能源并保持电压在规定区间为目标，每6 h利用可再生能源预测信息对逆变器Q-V下垂曲线的斜率进行集中整定，并在集中控制间隔期间利用整定后的Q-V下垂曲线实时调整无功输出，应对电压快速波动；文献[17]以光伏出力削减量最小为目标函数，利用集中控制分钟级调整Q-V下垂曲线的横轴截距，以达到逆变器在局部电压控制时全局最优的控制效果；文献[18]以网损最小和电压满足约束为目标，每15 min利用优化算法得到逆变器最优的无功输出参考值，各逆变器根据该参考值上下平移Q-V下垂曲线，使得逆变器在电压偏差较小时输出无功参考值，在电压偏差较大时跟随Q-V下垂曲线进行无功调整；文献[19]结合模型预测控制(model predictive control，MPC)算法，利用优化算法滚动调整Q-V下垂曲线电压死区节点位置，实现逆变器局部控制曲线的全局优化设置。

然而，上述方式在集中控制、局部控制阶段均存在不足。在集中控制阶段，上述方式没有充分考虑光伏出力预测(以下简称“光伏预测”)的不确定性对局部控制曲线集中整定的影响，在光伏预测存在误差时决策鲁棒性和经济性较差。在目前考虑光伏预测不确定性问题的优化策略研究中，分布鲁棒优化算法结合了随机优化与鲁棒优化的优点，能够更好地平衡决策经济性和鲁棒性，近年来受到了广泛关注[20-21]。在局部控制阶段，上述方式集中优化调节Q-V下垂曲线时，仅调整控制曲线斜率或截距，没有充分挖掘曲线可调灵活性，光伏逆变器的无功支撑能力没有被充分使用。

综上所述，本文提出基于动态调节下垂曲线的光伏逆变器集中-局部电压两阶段协调控制策略。所提策略集中控制阶段以电压越限条件风险价值(conditonl value at risk，CVaR)[22]与电压控制成本的加权和最小为目标函数，利用基于Wasserstein距离的分布鲁棒优化算法和MPC算法考虑光伏预测不确定性，根据集中优化结果滚动调节各光伏逆变器局部控制曲线，并在集中控制间隔时期，利用下垂曲线实时调整逆变器无功出力来抑制电压波动。此外，为了充分发挥逆变器的无功支撑能力，本文提出一种多曲线节点灵活可调的改进Q-V下垂曲线，使得逆变器在受局部控制曲线约束的情况下，也可以根据集中优化结果输出全局最优的无功功率。最后采用分布式光伏高渗透的改进IEEE 37节点配电系统验证本文所提策略的有效性。

1 集中-局部两阶段电压控制策略框架

本文提出的光伏逆变器集中-局部电压两阶段控制策略框架如图1所示。在集中控制阶段，根据设定的模型参数，以及获取的光伏和负荷预测数据，DSO采用分布鲁棒优化算法处理光伏预测不确定性，以电压控制成本与电压越限CVaR的加权和最小作为目标函数，以分钟级的尺度(例如5 min)，利用MPC算法滚动优化设置、动态调节各光伏逆变器有功功率削减量(以下简称“有功削减”)参考值和所提改进Q-V下垂曲线，并利用有限的通信设施，将优化结果下发给各光伏逆变器，使得各光伏逆变器在分钟级的尺度上实现电压控制的相互优化协调，达到全局最优的控制效果。在局部控制阶段，各光伏逆变器首先根据DSO下发的信号，调整有功削减和局部控制曲线，然后以秒级的尺度(例如10 s)测量本地节点电压，根据Q-V下垂曲线实时调整无功输出，实现对光伏预测误差和电压波动的快速响应。

图1 两阶段电压控制策略框架Fig.1 Framework of the proposed two-stage voltage control strategy

本文提出的光伏逆变器集中-局部电压两阶段控制策略具有以下优势：

a)所提控制策略能够克服使用固定局部控制曲线进行电压无功控制时，各光伏逆变器间难以协调、电压控制效果较差的问题。

b)所提控制策略能够克服仅使用集中控制方式时，控制策略无法快速响应电压波动的不足。

c)相比现有的集中与局部相结合的电压控制策略，本文所提控制策略利用分布鲁棒优化算法考虑光伏预测不确定性，实现DSO对电压控制和经济效益的不同权衡需求，进一步加强了DSO利用光伏逆变器对配电网电压进行调节的能力。

d)相比常规Q-V下垂曲线，所提改进Q-V下垂曲线多曲线节点灵活可调，具有更强的曲线调节和无功输出能力。在集中控制阶段优化调节所提改进下垂曲线，能够达到与使用集中优化直接设置逆变器无功出力值相同的电压控制效果。

2 局部控制阶段下垂曲线模型

2.1 常规Q-V下垂曲线

常规Q-V下垂曲线包括标准、变斜率以及变截距Q-V下垂曲线，具体的说明及其不足见附录A。

2.2 改进Q-V下垂曲线

针对常规Q-V下垂曲线无法充分发挥逆变器无功输出能力的问题，本文提出多曲线节点灵活可调的改进Q-V下垂曲线，曲线如图2所示，具体说明如下：①对于改进Q-V下垂曲线能够响应的最大、最小电压(图2中的节点电压Uq，1、Uq，6)，依然被设定为固定常数，即确保逆变器在任何运行场景，均能够根据本地测量电压快速响应和调整无功功率；②将逆变器开始发出/吸收无功功率的电压阈值(图2中的节点电压Uq，3和Uq，4)设定为由集中控制阶段整定的决策变量，相比使用标准Q-V下垂曲线，逆变器在一定程度上可根据运行场景动态调节无功输出能力；③将逆变器开始保持发出/吸收最大无功功率的电压阈值(图2中的节点电压Uq，2和Uq，5)设定为由集中阶段整定的决策变量，使得在电压偏差较小时，逆变器也能输出较大无功功率，进一步增强逆变器无功支撑能力，有效解决常规Q-V下垂曲线在高风险厌恶和高决策保守性的场景下，无功输出能力不足的问题。所提改进Q-V下垂曲线的灵活可调节点电压为Uq，k(k=2，3，4，5)，用下标k表示Q-V下垂曲线第k个节点相关参数，下同。图2中Q为无功功率，U为电压。

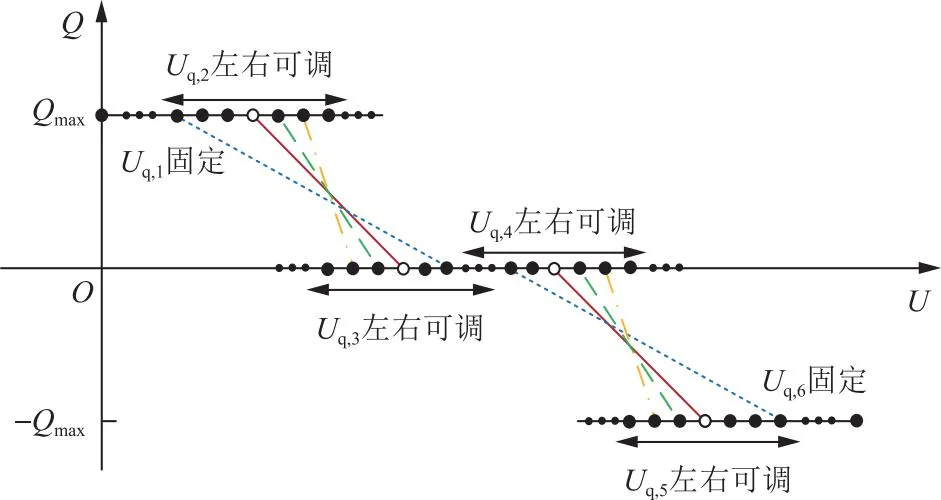
图2 改进Q-V下垂曲线Fig.2 Improved volt-var droop control curve

为了保证逆变器局部控制的稳定性，应限制所提改进Q-V下垂曲线的斜率和各曲线灵活节点位置关系。首先，Q-V下垂曲线的斜率不能过大，否则会导致无功输出对电压扰动过于敏感，引起电压控制稳定性较差问题；其次，各曲线灵活节点位置顺序应当保持不变，即Uq，k≤Uq，k+1(k=1，2，…，5)，确保电压无功控制负反馈逻辑不变；最后，应当对Q-V下垂曲线偏离标准曲线施加一定惩罚，避免下垂曲线频繁和不必要动作。所提改进Q-V下垂曲线控制稳定性约束在本文第3章中具体给出。

3 集中控制阶段优化模型

3.1 确定性优化模型

本研究以光伏逆变器有功削减比例、所提改进Q-V下垂曲线灵活节点位置以及储能装置有功功率为决策变量。首先在不考虑光伏预测不确定性的情况下，建立集中控制阶段确定性优化模型，在满足配电网运行约束和受控设备运行约束的同时，实现电压控制成本与电压越限CVaR加权和最小的优化目标。

3.1.1 确定性优化模型目标函数

集中控制阶段确定性优化模型采用风险系数ρ，将最小化电压控制成本和电压越限CVaR的多目标问题转化为单目标问题，具体如下：

min(JCost，t+ρJCVaR，t)，

(1)

JCost，t=f1，t+f2，t+f3，t+f4，t=

(2)

[Un，t(Pc，PV，t)-Umax-kn，t]+}.

(3)

式中：t为集中控制时间点，用下标t表示t时的相关参数，下同；JCost，t为配电网的电压控制成本，权重为1，其包括与上层电网的电力交易成本f1，t、逆变器无功出力成本f2，t、光伏出力削减惩罚成本f3，t，以及逆变器Q-V下垂曲线变动惩罚成本f4，t，设置f4，t的目的是避免下垂曲线的不必要和频繁动作；JCVaR，t为配电系统电压越限CVaR；风险系数ρ为DSO对于电压越限风险的重视程度，即CVaR的权重；n为配电网节点，用下标n表示配电网节点n的相关参数，下同；Nbus为配电网所有节点集合；αn，t为逆变器有功削减比例，为决策变量；E(·)为期望函数；函数[·]+的功能为与0比较后取较大值；PL，n，t、PPV，n，t分别为有功负荷、光伏可用有功功率，当节点没有光伏单元时，PPV，n，t=0；Pc，PV，n，t则为光伏可用有功功率预测值，用下标c表示相关参数预测值，下同；PB，n，t为储能装置有功功率吸收值，为决策变量；QPV，n，t为逆变器无功功率注入值，当节点没有光伏单元时，QPV，n，t=0；Un，t为节点电压幅值；Umax为节点电压上限，用下标max、min表示参数的最大、最小值，下同；Uq，0，k为常规Q-V下垂曲线第k个节点电压值；c1，n，t和c2，n，t为购卖电成本系数，c3，n，t、c4，n，t、c5，n，t则分别为无功出力成本系数、有功削减惩罚成本系数，以及Q-V下垂曲线调节惩罚成本系数；β为电压越限CVaR中节点电压在限制范围内的置信度；kn，t为电压越限CVaR辅助变量；p(PPV，t)为光伏可用有功功率向量PPV，t的概率；Pc，PV，t为光伏可用有功功率预测值向量。由于优化模型为确定性模型，光伏可用有功功率向量唯一且取为预测值Pc，PV，t，即p(Pc，PV，t)=1。

3.1.2 确定性优化模型约束条件

集中控制阶段确定性优化模型约束条件包括光伏逆变器运行约束、节点电压约束、储能装置运行约束，以及所提改进Q-V下垂曲线约束。

a)光伏逆变器运行约束。光伏逆变器无功支撑能力受逆变器容量和有功输出的限制，并且有功削减不能超过最大可用有功功率，约束分别为：

(4)

0≤αn，t≤1，∀n∈NPV.

(5)

式中：NPV为配电网中具有光伏逆变器的节点集合；SPV，n为光伏逆变器容量。

b)节点电压约束。DSO若更加重视电压控制成本，将允许一定的电压偏高甚至越限，电压偏高和越限的严重程度由式(3)量化；DSO若更加重视电压越限风险，将会调整光伏逆变器有功削减和无功出力，降低节点电压，但是降低节点电压应有所限制，否则会导致电压越下限问题。电压限制约束式为：

Umin≤Un，t，∀n∈Nbus.

(6)

c)储能装置运行约束。本研究将蓄电池作为储能装置接入配电网，并设蓄电池逆变器工作在单位功率因数模式，储能装置运行约束相关公式和具体说明参见附录B。

d)改进Q-V下垂曲线约束。如图2所示，所提改进Q-V下垂曲线为分段线性曲线，可以通过引入辅助变量，精确描述逆变器无功出力受该曲线的控制，约束式为：

(7)

式中：Uq，n，k，t(k=1，6)为常数，Uq，n，k，t(k=2，3，4，5)为连续变量；aq，n，k，t、dq，n，k，t分别为辅助连续变量、二元变量；Qq，k为图2中节点电压Uq，n，k，t对应的无功功率，均为常数；Qn，max为节点n逆变器的最大无功出力。由于逆变器具备削减有功功率能力，一方面为了充分调用削减有功功率所产生的额外无功调度空间，另一方面为了简化优化模型，尽可能地减少连续变量相乘产生的非线性项，设置Qn，max=SPV，n。

所提改进Q-V下垂曲线的控制逻辑和斜率限制约束为：

(8)

式中mq，1、mq，2分别为下垂曲线的左半部分斜率限制系数、右半部分斜率限制系数，mq，1和mq，2均设置为0.02(标幺值)。

3.2 考虑光伏预测不确定性的优化模型

本研究利用基于Wasserstein距离的分布鲁棒优化算法考虑光伏预测不确定性，并使用MPC算法闭环滚动优化，进一步纠正光伏预测误差造成的集中控制阶段电压控制偏差，提高优化控制准确度。

3.2.1 基于Wasserstein距离的模糊集

不确定性优化模型利用Wasserstein距离描述模糊集中经验概率分布与真实概率分布之间的距离，与建立其他模糊集的方式相比，能够更全面地挖掘光伏预测有限数据中真实概率分布的深层信息[23]，同时，基于有限数据集，利用Wasserstein距离构建模糊集的分布鲁棒优化算法，该模型能够通过对偶理论被转化为易于求解的有限凸规划模型[24]；因此，本研究以Wasserstein距离作为半径，以根据光伏预测误差有限数据集获取的经验概率分布为中心，将光伏预测误差真实概率分布限制在球型空间模糊集中。DSO可以通过调整Wasserstein半径控制模糊集空间的大小，来调整优化结果的保守度。

经验概率分布p1和真实概率分布p2之间的Wasserstein距离

(9)

式中：S为ξ1和ξ2的联合概率分布，p1和p2称为S的边际概率分布；V(ξ1，ξ2)为S的全体集合；ξ1、ξ2分别为p1、p2的随机向量，取值集合均为G={ξ∈RB：cξ≤d}，其中c、d分别为随机向量取值集合的系数矩阵、向量，随机向量ξ代表光伏预测误差向量，B为ξ的长度；G2为二维随机向量(ξ1，ξ2)所有的取值集合；‖·‖表示取范数计算。

当随机向量的有限数据集GN(包含的样本数量为N)已知时，基于Wasserstein距离的模糊集

W(pG，N)={p∈J(G)：dW(pG，N，p)≤ε}.

(10)

式中：pG，N为根据GN生成的经验概率分布，用下标G表示与光伏预测误差数据集GN相关的参数，下同；p为模糊集包含的概率分布；J(G)为G的全部概率分布集合；ε为W中包含的概率分布和pG，N之间的最大Wasserstein距离，即W的半径。ε与W包含真实概率分布的置信度λ的关系为

(11)

式中C为与GN相关的常数。

根据式(10)、式(11)，DSO可以通过调整ε来调整W的大小，进而控制决策鲁棒性和经济性。

在本研究中，B等于光伏逆变器数量。当光伏预测误差向量为GN中的样本，即ξG∈GN时，实际光伏可用有功功率

PG，PV，n，t=Pc，PV，n，t+ξG，n，t，∀n∈NPV.

(12)

式中ξG，n，t为向量ξG，t中的元素。

3.2.2 模型预测控制算法

在分布式光伏高渗透率配电网中，无法保证实际光伏出力与预测值相同，并且光伏预测精度随着预测步长的增加显著降低，导致以常规开环控制方式求解的超前控制指令不再可行；因此，本研究采用MPC算法，以闭环优化的方式，不断更新光伏预测信息，滚动求解电压控制优化问题，及时校正集中控制指令。MPC算法具体说明参见附录C。

3.2.3 不确定性优化模型目标函数

不确定性优化模型计及光伏预测不确定性对于电压越限CVaR的影响，根据模糊集中使得电压越限CVaR最恶劣的概率分布，对决策变量进行滚动优化，目标函数式(1)—式(3)相应更改为：

(13)

[UG，n，τ(PG，PV，i，τ)-Umax-kn，τ]+}，

(14)

(1-αn，τ)PG，PV，i，n，τ]++c2，n，τ[PL，n，τ+PB，n，τ-

(15)

式(13)—(15)中：T为MPC算法中预测时域长度；τ为时间变量，用下标τ表示τ时的相关参数；EGN，τ(·)为基于数据集GN，τ求期望的函数；Epτ(·)为基于概率分布pτ求期望的函数；下标i表示对随机向量有限数据集GN进行索引。

3.2.4 不确定性优化模型约束条件

本研究利用期望形式考虑光伏逆变器容量限制约束和节点电压约束受光伏预测不确定性的影响，约束式(4)、式(6)相应更改为：

∀n∈NPV，τ∈{t，…，t+T}；

(16)

Umin≤EGN，τ(UG，i，n，τ)，∀n∈Nbus，

τ∈{t，…，t+T}.

(17)

不确定性优化模型其余约束不涉及到随机变量，与确定性优化模型相同。

3.2.5 不确定性优化模型求解

在不确定性优化模型中，节点电压需要通过交流潮流计算得到，计算式是注入功率的非凸非线性方程；并且在改进Q-V下垂曲线方程式(7)中，也存在因连续变量交叉相乘而导致的双线性项；此外，在利用分布鲁棒优化算法处理光伏预测不确定性时，目标函数为min-max形式：因此，该模型为混合整数非凸非线性模型，难以直接求解。

本研究首先对节点电压方程进行线性化处理[25-26]，然后采用连续变量离散化的方式对式(7)中存在的双线性项进行线性化处理[27]，最后采用文献[24]提出的分布鲁棒优化模型凸重构方法，对本文所提优化模型进行凸重构。经过线性化处理和凸重构后的模型如式(18)所示，为混合整数二阶锥模型，可以调用商业求解器直接求解。本研究基于MATLAB仿真平台，使用CVX优化器接口调用商业求解器GUROBI直接求解该模型，收敛精度均设置为0.1%。

(18)

式中：λn，τ、sn，i，τ分别为分布鲁棒优化模型凸重构时引入的辅助变量；xτ为式(13)中第1阶段的决策变量向量，即xτ=((ατ)T，(PB，τ)T，(QPV，τ)T)T，其中ατ为光伏逆变器有功削减比例决策向量，PB，τ为储能装置有功功率决策向量，QPV，τ为逆变器无功功率决策向量；bn，l，τ、an，l，τ均为分布鲁棒模型凸重构辅助变量，具体表达式如式(19)所示；lq，n，k，m，τ、wq，n，k，m，τ分别为双线性项线性化二元、连续辅助变量；M为足够大常数；下标m为改进Q-V下垂曲线约束线性化过程中引入的变量索引；下标l表示将函数[·]+分类讨论后的公式索引。

(19)

式中：1、0分别为元素全为1、0的nbus维向量，nbus为配电网节点总数；R、X分别为配电网节点阻抗矩阵实部、虚部；gn、hn分别为矩阵G、H第n行(对应第n个节点)构成的向量，G、H为节点电压方程线性化过程中引入的系数矩阵；Ubase为配电网节点基准电压向量，本研究取注入功率为0时的节点电压向量；|Ubase|、θbase分别为Ubase的幅值、相角，Ubase，n为Ubase中的第n个量。

4 集中-局部两阶段电压控制策略流程

得益于集中、局部两阶段电压控制方式的相互配合，DSO既能充分利用通信设施，全局优化协调各光伏逆变器，也能利用局部控制曲线使得各逆变器出力进行自适应调整。图3所示为所提两阶段电压控制策略的流程。

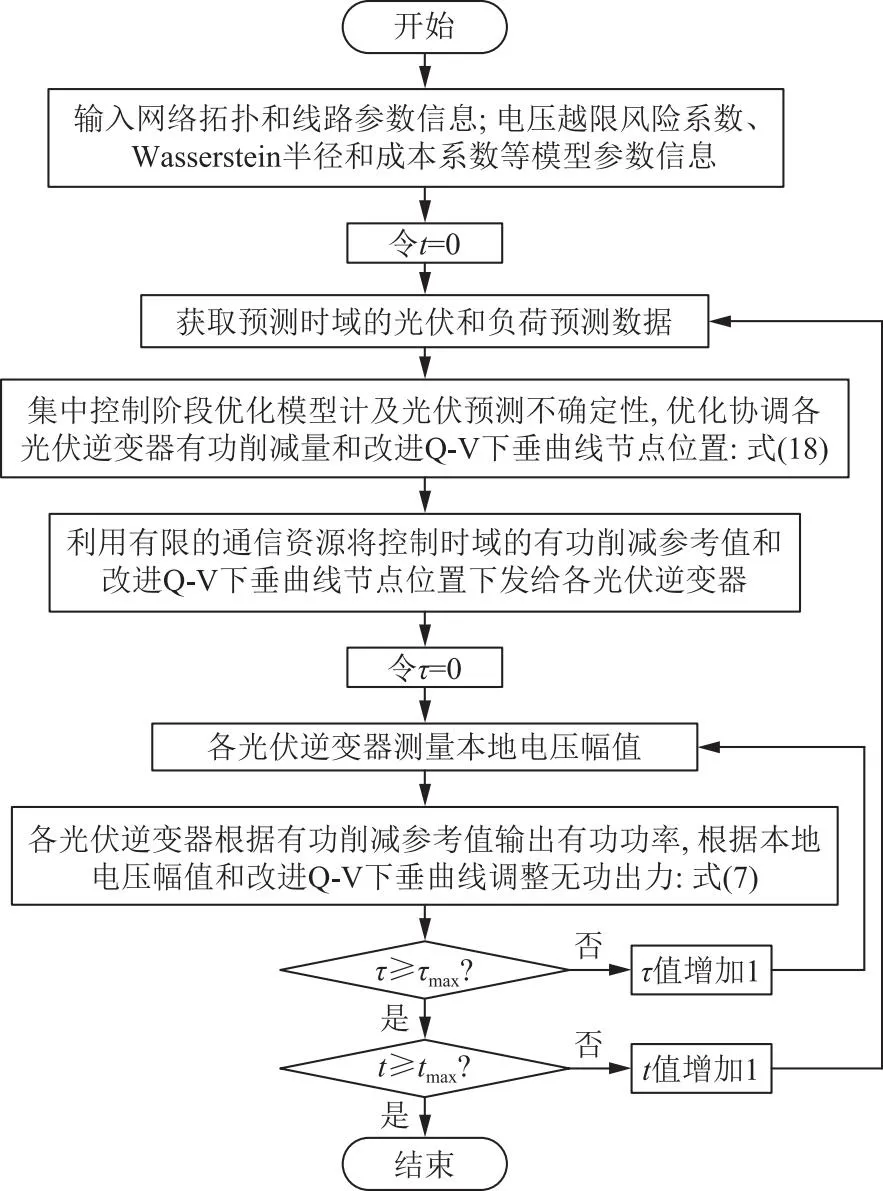
图3 所提两阶段电压控制策略流程Fig.3 Flow chart of the proposed two-stage voltage control strategy

5 算例分析

5.1 算例介绍

本研究对含有11个光伏逆变器(PV1—PV11)和4个储能装置(EB1—EB4)的改进IEEE 37节点配电系统进行仿真，系统拓扑如图4所示，线路参数和负荷数据与文献[28]一致，配电系统的基准电压为4.8 kV，节点1为松弛节点，电压幅值设定为1.02(标幺值)，电压相角设定为0°，光伏逆变器和储能系统的位置和容量信息参见附表D.1，其余仿真参数参见附表D.2。取集中控制时间间隔Δt=5 min，测试系统24 h总负荷和总光伏有功功率曲线如图5所示，该配电网的光伏渗透率达到了210%(最大光伏可用出力除以最大负荷需求)。在光伏预测数据方面，每个Δt设置30条预测样本，即N=30，并且总体上预测误差随着预测步长的增加而增大。

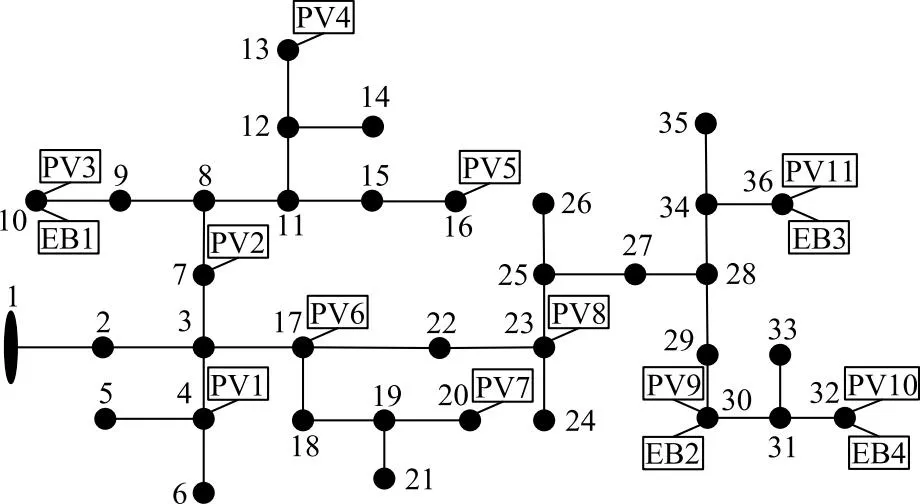
图4 改进的IEEE 37节点配电系统Fig.4 Modified IEEE 37-bus distribution network system

图5 总负荷和总可用光伏有功功率曲线Fig.5 Total load demand and available PV output curves

5.2 集中控制效果分析

为验证所提策略相较于使用固定局部控制曲线进行电压无功控制的优越性，同时验证在集中控制阶段使用所提改进Q-V下垂曲线后，逆变器具有更加灵活的无功支撑能力，设定风险系数ρ=15，Wasserstein半径ε=0.001，在不同光伏场景下，对光伏逆变器采用如下4种基于不同Q-V下垂曲线的集中控制策略进行仿真分析：

策略1：光伏逆变器无功出力遵循附图A.1所示的标准Q-V下垂曲线，曲线节点参数参见附表D.2。

策略2：光伏逆变器无功出力遵循附图A.2所示的变斜率Q-V下垂曲线，曲线固定节点与策略1标准Q-V下垂曲线相同。

策略3：光伏逆变器无功出力遵循附图A.3所示的变截距Q-V下垂曲线，曲线斜率与策略1标准Q-V下垂曲线相同。

策略4：光伏逆变器无功出力遵循如图2所示的改进Q-V下垂曲线，曲线固定节点与策略1标准Q-V下垂曲线相同。

进一步设置不考虑局部控制曲线约束的集中控制策略5作为光伏逆变器无功出力最优策略。

图6—图8分别展示不同光伏场景下的末端节点电压以及光伏逆变器无功出力和有功削减情况。

图6 不同光伏场景末端节点电压Fig.6 Terminal bus voltage in different PV scenarios

图7 不同光伏场景逆变器无功出力Fig.7 Total reactive power output of inverters in different PV scenarios

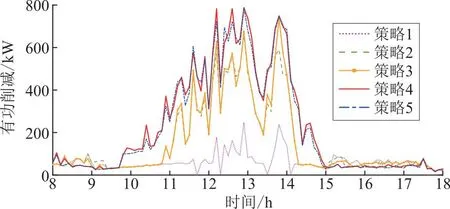
图8 不同光伏场景逆变器有功削减Fig.8 Total curtailed active power of inverter in different PV scenarios

由图6—图8可知，在高光伏出力导致节点电压偏高的时段，策略1因标准Q-V下垂曲线节点电压与无功出力呈固定反比关系，当节点电压降低时，无功出力相应减少，此时需要削减更多的有功功率维持较低的节点电压；因此，出于对经济效益和电压越限风险的权衡，策略1无功出力和有功削减均较少，末端节点电压维持在较高水平，节点电压在多个时间段超越上限。

策略2、策略3可以通过集中控制分别动态调节Q-V下垂曲线的斜率、截距，打破了标准曲线节点电压和无功出力固有的反比关系，使得各光伏逆变器在一定程度上相互协调无功出力，逆变器在节点电压降低时，无功出力维持不变甚至增加；因此，相比于策略1，策略2和策略3在仅增加了较少有功削减的情况下，输出了较多的无功功率，大幅降低了节点电压及其越限风险。

图9所示为策略4末端节点光伏逆变器Q-V下垂曲线节点变化情况。

图9 不同光伏场景策略4末端节点下垂曲线变化情况Fig.9 Variation of terminal inverter droop curves of strategy 4 in different PV scenarios

根据图9可知，本文所提策略4使用的改进Q-V下垂曲线兼顾了变斜率和变截距的功能，曲线节点Uq，k(k=2，3，4，5)均可灵活调节，使得各逆变器无功支撑能力和相互之间的电压控制协同能力得到进一步提升。如图6所示，在08：00—11：00和15：00—18：00，节点电压相较于11：00—15：00偏低；但是得益于所提改进Q-V下垂曲线节点调节的灵活性，根据图7分析可知，策略4光伏逆变器在维持较低的电压越限风险和总成本时，仍能发出较多的无功功率，这是策略2仅动态调节Q-V下垂曲线斜率和策略3仅动态调节Q-V下垂曲线截距所无法做到的。

各策略与策略5具体对比统计见表1，相比于其他策略，策略4和策略5的节点电压、无功出力、有功削减和成本情况均十分接近。

表1 不同控制策略决策变量和成本情况与策略5对比统计Tab.1 Decision-making variables and costs of different control strategies compared to strategy 5

综上所述，在不同光伏场景下，本文所提策略在集中控制阶段通过优化调节所提改进Q-V下垂曲线，能够使得各光伏逆变器之间相互协调，达到全局最优的电压控制效果。

5.3 局部控制效果分析

为了验证本文所提控制策略相比于仅使用OPF算法的集中控制策略在电压波动抑制方面的有效性，在ρ=10且其余参数与5.1节相同情况下，策略4和策略5选择相同时间点的局部控制曲线参数和无功出力参考值，并且2种策略具有相同的有功削减。光伏出力波动如图10所示，分别在经历70 s、160 s和270 s后，光伏出力均出现了明显的波动，波动率超过了63.9%。设置局部控制步长为10 s，仿真总时长为5 min。

图10 光伏出力波动Fig.10 PV output fluctuations

2种策略的末端节点电压波动情况如图11所示，2种策略的电压均受到了光伏出力波动的影响，策略5的电压波动率为5.88%。逆变器无功出力情况如图12所示，策略4根据电压波动情况，通过所提改进Q-V下垂曲线实时调整逆变器无功出力，电压波动率为3.50%，相比策略5电压波动降低了40.56%。此外，由于电压波动，策略5还出现了若干个时间点出现电压越限的问题，而策略4得益于逆变器无功出力的快速调节，有效抑制了电压波动问题。

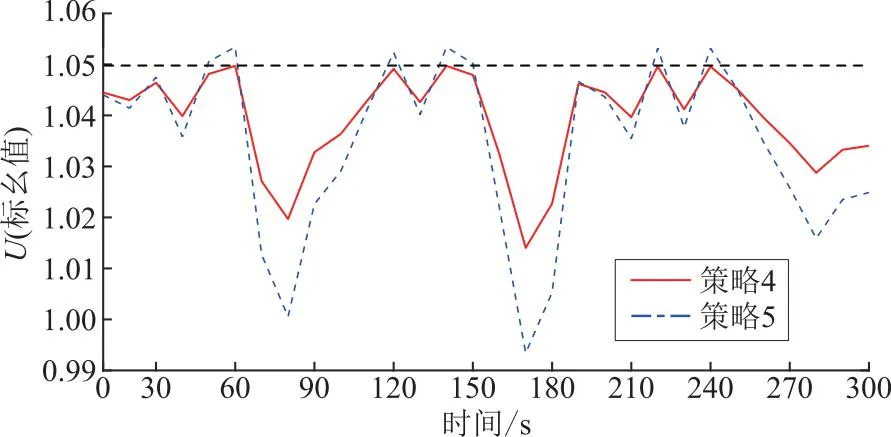
图11 2种控制策略末端节点电压波动Fig.11 Terminal bus voltage fluctuations of two control strategies

图12 2种控制策略末端节点逆变器无功出力Fig.12 Reactive power output of the inverter in terminal bus of two control strategies

综上所述，使用本文所提基于动态调节下垂曲线的集中-局部电压两阶段控制策略，相比于仅使用OPF算法的集中电压控制策略，电压波动得到了有效抑制，电压越限亦可避免。

5.4 不同Wasserstein半径场景控制效果分析

不同Wasserstein半径ε的选取会影响对光伏预测误差概率分布的模糊集W大小的描述，进而影响集中控制阶段分布鲁棒优化模型决策的保守度。设定ρ=10，其余参数与5.1节相同，在13：00时刻不同Wasserstein半径ε下，集中优化得到的不同控制策略逆变器无功出力、有功削减以及末端节点电压和总成本曲线分别如图13—图16所示。

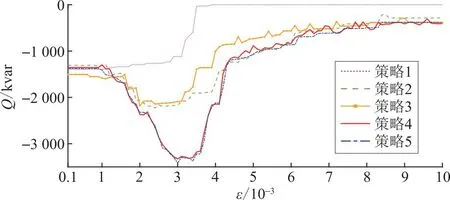
图13 不同Wasserstein半径逆变器无功出力Fig.13 Total reactive power output of inverter with different Wasserstein radius

图14 不同Wasserstein半径逆变器有功削减Fig.14 Total curtailed active power of inverter with different Wasserstein radius

从图13—图16可以看出，随着ε的增大，5种控制策略的总成本和总光伏出力削减量不断增大，末端节点电压不断降低，因此决策变量总体上随着ε的增大而趋于保守，鲁棒性不断增强。策略4在不同ε下的优化结果与基于光伏预测期望值的确定性优化结果、常规鲁棒优化结果的对比见表2。当ε趋于0时，W中仅包含一种概率分布，即认为光伏预测误差有限数据集GN中的样本所形成的概率分布为真实概率分布，此时优化结果与基于光伏预测期望值的确定性优化结果接近，经济效益较好，但节点电压较高(如图15所示)，甚至超过了电压上限1.05(标幺值)；ε越大，则W中所包含的概率分布与基于GN的经验概率分布差距越大，此时优化结果越接近常规鲁棒优化结果，经济性越差，但节点电压较低(如图15所示)，电压越限风险越小。除此之外，如图13所示，光伏逆变器无功出力在ε较小和较大的情况下均较低，这分别是由DSO对经济效益的权衡和电压控制下限约束式(17)导致的。

表2 策略4不同优化方式对比Tab.2 Comparison of different optimization methods of strategy 4s

图15 不同Wasserstein半径末端节点电压Fig.15 Terminal bus voltage with different Wasserstein radius

图16 不同Wasserstein半径总成本Fig.16 Total costs with different Wasserstein radius

综上，在使用分布鲁棒优化算法处理光伏预测误差后，DSO可以通过调整Wasserstein半径ε，在电压控制成本与光伏预测不确性带来的电压越限风险之间进行充分权衡，相比确定性优化和鲁棒优化，分别具有更好的鲁棒性和经济性。

接下来进一步对比分析不同控制策略在不同ε下的控制效果。如图13—图16所示，在不同的ε下，策略1的逆变器无功出力、有功削减以及节点电压与策略5的全局最优结果相差较大，并且策略1的总成本最大，再次证明利用固定局部控制曲线进行电压控制时，无法使得各逆变器无功出力相互协调，控制效果较差。

相比逆变器无功出力较多的情况，在逆变器无功出力较少的情况下，策略2和策略3的逆变器无功出力、有功削减以及节点电压与策略5的全局最优结果更加接近，证明了通过集中控制方式动态调节Q-V下垂曲线，能够使得各逆变器间相互协调，达到全局最优的电压控制效果。然而，当集中控制需要逆变器进一步提供无功支撑时，由于策略2的变斜率Q-V下垂曲线和策略3的变截距Q-V下垂曲线调节灵活性有限，此时无法进一步提高无功输出达到全局最优的电压控制效果。策略4采用本文所提改进Q-V下垂曲线，相比于策略2和策略3可以通过进一步调节曲线节点Uq，2和Uq，5释放无功支撑能力，在所有ε下均能达到与策略5相似的全局最优控制效果，证明了所提改进Q-V下垂曲线的有效性和灵活性。

6 结论

在分布式光伏高渗透率配电网中：仅使用OPF算法进行光伏逆变器集中控制，无法及时抑制电压波动；仅使用局部控制，无法达到全局最优控制效果；使用集中和局部结合的控制方式时，常规Q-V下垂曲线可调节灵活性没有被充分挖掘，逆变器无功支撑能力有限；并且现有文献没有充分考虑光伏预测不确定性对于电压越限风险的影响，以及DSO在不同的电压控制成本和电压越限风险之间进行权衡的需求。综上，本文提出了基于动态调节下垂曲线的光伏逆变器集中-局部电压两阶段协调控制策略，主要结论如下：

a)本文所提策略相较于逆变器集中电压控制策略，能够利用下垂曲线实时调整逆变器无功出力响应光伏变化，达到抑制电压波动和防止电压越限的效果；相较于逆变器局部电压控制策略，能够根据不同的运行场景全局动态调节下垂曲线，实现光伏逆变器间电压控制的优化协调。

b)本文所提控制策略采用基于Wasserstein距离的分布鲁棒优化算法和MPC算法，考虑光伏预测不确定性对于电压控制的影响，使得DSO可以通过控制Wasserstein半径，对光伏逆变器电压集中控制的经济效益和越限风险进行权衡和调整。

c)本文所提改进Q-V下垂曲线具有多个灵活可调曲线节点，相比于常规Q-V下垂曲线，能够在不同光伏场景、不同Wasserstein半径场景，满足集中控制对于逆变器无功出力的需求，达到接近全局最优的逆变器电压控制效果。