计及时空分布特性的光-荷典型场景提取方法

钟富城，王星华，黎子律，张岚麒，杨炜康，黄祥源，赵卓立

(广东工业大学 自动化学院，广东 广州 510006)

随着我国“双碳”目标以及屋顶光伏整县工作的推进，越来越多的屋顶分布式光伏接入配电网中[1-3]。分布式光伏出力随机性较大，与气象条件有着很强的相关性。分布式光伏对配电网的高渗透率会对电力系统的调度优化控制提出更高的要求[4-5]。准确描述含大规模分布式光伏的配电网光伏、负荷典型日运行场景，是提升光伏就地消纳能力与配电网安全可靠运行能力的前提。

典型场景法是当前描述含不确定性光伏出力运行场景的主要手段，其主要分为数学统计学和聚类方法2种。基于概率密度函数的方法利用数学统计方法对历史光伏、负荷数据进行处理，得出满足历史光伏、负荷数据分布特性的公式或曲线：文献[6]利用蒙特卡洛抽样法生成光伏发电中的随机分量，结合理想出力归一化曲线与随机分量生成光伏发电序列；文献[7]利用copula函数构建光伏-风电相关性模型后，采用改进的拉丁超立方抽样法生成大量光伏-风电场景，最后结合k-means聚类法完成典型场景生成；文献[8]基于copula理论构建出符合历史分布特性的光伏和负荷的关联公式，从而完成光-荷联合，根据关联公式为含光伏的配电网提供规划参考。基于聚类分析的方法是一种实现簇内相似度更大和簇间相似度更小，以揭示样本之间内在性质的算法：文献[9]利用k-means聚类算法分别对各节点的负荷、光伏和风电数据进行聚类，并以聚类中心作为该节点的典型场景；文献[10]基于局部密度中心的聚类算法对光伏历史出力数据进行聚类分析，以聚类中心为典型出力场景，再利用copula函数建立描述典型场景间相关性的公式。

以上方法在对单一节点的典型场景生成时有较好的效果，但未能很好地考虑配电网中各台区节点之间光伏出力、负荷功率之间的时间和空间分布特性。因此本文提出一种计及时空分布特性的光-荷典型场景提取方法，考虑配电网的空间拓扑结构，建立计及节点负荷时空分布特性且能整体反映光伏、负荷日场景的描述矩阵，并基于拉普拉斯特征映射(Laplacian eigenmaps，LE)和高斯混合模型(Gaussian mixture model，GMM)估计，完成光-荷典型日场景提取，生成能为配电网的运行调度和规划等工作提供参考的光-荷典型日场景。

1 基于LE矩阵降维

为了能一次性建立整个中压配电网或一整条馈线上所有台区的光伏、负荷典型场景，避免每次只能单独形成1个台区典型场景的缺点，本文提出基于LE及GMM的计及时空分布特性的光-荷典型场景联合方法。主要步骤如图1所示。

图1 本文所提方法主要步骤Fig.1 Main steps of the proposed method

1.1 光-荷日运行场景描述矩阵

本文所需数据为完整1年中每日24 h各时刻的光伏、负荷数据。利用3次样条插值法[11]对缺失少量数据的日期进行填充，并舍弃缺失过多数据的日期，最终得到1年中具备完整24 h光伏、负荷运行数据的日期，保证形成的日运行场景描述矩阵之间行、列完整且相同，便于后续计算矩阵的降维和概率密度时，避免由于矩阵结构不一致带来的降维值不可用的影响。

图2所示为1个已知拓扑结构的中压配电网(其中PV表示光伏)，共有10个负荷节点，其中有4个节点有光伏接入。

图2 配电网拓扑结构示意图Fig.2 Schematic diagram of distribution network topology

根据图2建立光伏、负荷的日场景矩阵描述，如下：

(1)

式中：p为光伏出力或负荷功率；下标n表示节点编号。日场景描述矩阵的每1列表示1个节点，每1行表示节点采样时刻记录的出力数据。分别建立能够反映配电网时间断面下负荷、光伏出力节点分布情况的日运行场景，将整个配电网或整条馈线所有台区的场景都包含在描述矩阵中。该场景描述矩阵的每行之间很好地体现了各节点光伏出力和负荷水平的时序相关性特征，每列之间很好地体现了各节点之间的空间相关性。

此外，这种光伏、负荷日场景描述矩阵通过新增列数或建立新的矩阵来描述同一配电网结构中光伏、负荷节点新增的情况，不仅可以很好地反映配电网光伏、负荷的时空分布特性，且充分考虑了二者的增长特性。

1.2 基于LE的矩阵降维

由于光伏、负荷日场景描述矩阵的每行、每列之间包含了节点之间光伏出力、负荷功率的时序相关性和空间相关性特征[12-14]，若简单使用投影类型降维法(如将三维矩阵投影到二维平面)，则在整体上丢弃了某个维度的信息特征，使矩阵信息失真过大而失去参考价值。为保留描述矩阵的流形结构特征，且不过多丢失矩阵的重要信息，应避免选用投影类降维法。本文选用基于流形学习的LE法来描述矩阵的降维要求。

LE是运用图拉普拉斯概念来计算高维特征集的低维流形表示的非线性流形学习降维算法[15-16]，其实质是找到平均意义上保持数据点局部邻近信息的特征表示。LE算法所产生的映射可以看作是对几何流形的一种连续离散逼近的映射，用数据点的邻域图来近似表示流形，并用Laplace-Beltrami算子近似表示邻域图的权值矩阵，可实现高维流形的最优嵌入。其基本实现步骤如下：

步骤1，构建图。对于1个矩阵内部的数值，将每个数据点与近邻的k个数据点连线，其中k为预先设定的值，由此将所有的数据点连接构建1个图。

步骤2，确定权重。确定数据点之间连线的权重大小，构成邻接矩阵Wij；若点i和点j相连，则二者关系的权重设定如下：

(2)

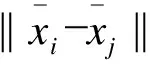
步骤3，构建拉普拉斯矩阵。定义对角矩阵D，对角线上(i，i)位置元素等于矩阵Wij的第i行之和。则拉普拉斯矩阵L=D-Wij。

步骤4，确定目标函数。为了让样本yi和yj在降维后的子空间里尽量接近，优化目标函数为min∑‖yi-yj‖2wij，wij为i和j之间的权重值；利用Lagrange乘子法将目标函数化简为Lyi=λDyj。

步骤5，特征映射。计算拉普拉斯矩阵L的特征向量与特征值λ：Lyi=λDyj，其中Dyj为步骤3中D的yj样本矩阵，Lyi为yi样本矩阵，使用最小的m个非零特征值对应的特征向量Ly作为降维后的结果输出。

由于后文高斯混合模型在处理高维数据时计算复杂度急剧增加，且容易出现维度灾难问题，导致估计结果不准确，而其对一维数据的估计效果是最佳的，所以本文对24行n列的矩阵降维到一维，再分别组成用于高斯混合模型计算的光伏、负荷矩阵降维值的数据集。由于每个矩阵内部都呈现不一样的流形结构，对每个矩阵做相同降维处理后的数值仍能表征矩阵的流形结构差异。

2 基于GMM的典型场景提取

GMM是一种常用的概率模型，用于对具有未知或复杂分布的数据进行建模，从而计算其数据分布特征，最终基于多个高斯分布的线性组合来描述数据的概率分布[17-19]。对于LE形成的光伏、负荷矩阵降维值数据集，由于内部降维值的分布特征未知，可认为其总体分布中含有K个子分布概率模型。针对数据分布特征未知的数据集，为了准确得出矩阵降维值数据分布特征，本文采用GMM进行计算，其数学表达式如式(3)所示：

(3)

高斯密度函数

(4)

GMM的计算具体步骤如下：

步骤1，初始化。假定数据集内部共有K种子分布，随机初始化每种分布的均值、协方差和权重参数。

步骤2，期待步骤。根据当前模型参数，计算每个数据点属于每个分布的后验概率，然后使用参数的当前估计评估似然函数。

步骤3，最大化步骤。根据期待步骤的结果更新模型参数，即通过最大化似然函数来调整每个高斯分布的均值、协方差矩阵和权重系数。

步骤4，重复步骤3，直至模型收敛或达到预定的迭代次数。

步骤5，根据训练好的模型参数可视化处理模型。

对于光伏、负荷的日场景描述矩阵的降维值数据集，使用上述GMM计算，即可分别得出光伏、负荷日场景的概率分布情况，并选取光伏、负荷数据集中概率密度较大的场景作为候选典型场景集。

2.2 基于Wasserstein距离的典型场景提取

在初步完成典型场景候选集识别后，为了减少候选集场景中虽然满足概率阈值要求但场景矩阵内部数据分布差别不大的场景数量，提高典型场景的代表性，本文利用Wasserstein距离指标来衡量候选典型场景集之间的相似程度[20-21]，并最终舍弃部分虽然满足概率阈值要求但相似性较大的冗余场景，得出具有高度代表性并与其他典型日场景有较大区别的典型日场景。

Wasserstein距离可以用来衡量2个分布的相似程度，数据从分布p移动成分布q所移动距离的最小值即为2个分布间的Wasserstein距离。本文利用Wasserstein距离衡量矩阵之间的相似程度，2个矩阵之间的Wasserstein距离越小表明矩阵间的相似程度越高，其公式如下：

(5)

式中：Π(p，q)为分布p和q组合起来的所有可能的联合分布的集合，对于每一个可能的联合分布γ，可以从中采样得到任一对样本(x，y)，并计算出这对样本的距离。最终计算出该联合分布γ下，样本对距离的期望值Ex，y～γ(‖x-y‖)。在所有可能的联合分布中能够对这个期望值取到的下界就是2个分布间的Wasserstein距离。

在本文中，若2个候选场景集矩阵间的Wasserstein距离过小，表示2个日场景描述矩阵比较相似，应取其中概率密度更高的作为典型场景。具体Wasserstein距离下限的设置，可在1年的光伏典型场景数量5～10个、负荷典型场景数量7～12个的规模之间进行调整，这样的光-荷典型场景规模比较适合配电网运行规划[22-24]。

3 算例分析

为了验证本文方法的有效性，选取广东省清远地区某条含光伏接入的10 kV馈线2021年的光伏、负荷运行数据进行实验仿真。该馈线共有10个负荷节点，其中包含4个光伏节点，拓扑结构如图2所示，各台区节点容量见表1。

表1 各节点变压器容量及光伏装机容量Tab.1 Transformer capacity and PV installed capacity at each node

首先对所有收集到的运行数据进行预处理，按上文所述方法填充部分缺失值，舍弃缺失值过多的日期。进而按照该配电网的拓扑结构分别建立光伏、负荷近1年运行日的日场景描述矩阵。

3.1 典型场景提取

本文使用PyCharm集成开发环境进行实验仿真。LE邻域值设置为3，维数设置为1；混合高斯分布K值初始化设置为5。首先分别对光伏、负荷的日场景描述矩阵进行降维处理得到光伏、负荷降维值数据集；随后利用GMM分别计算2个数据集的概率密度分布情况，得到结果如图3、图4所示。

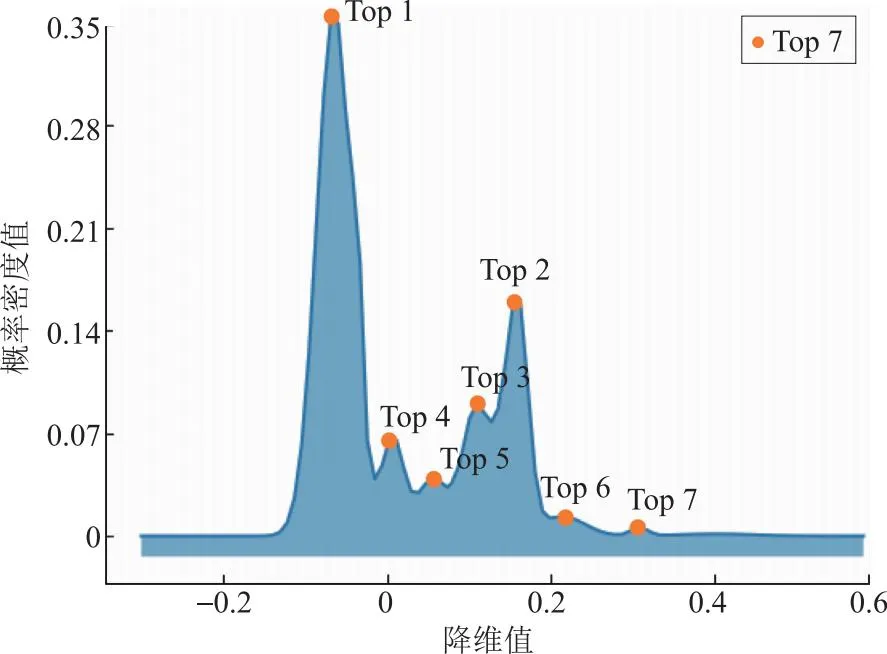
图3 光伏典型日场景的概率分布Fig.3 Probability distribution in typical PV daily scenarios

图4 负荷典型日场景的概率分布Fig.4 Probability distribution in typical load daily scenarios

由图3可以提取出光伏候选典型场景矩阵7个(记为Top1—Top7)，Top6和Top7仅占4.75%，故予舍弃。剩下5个候选场景在经过Wasserstein距离指标筛选后，最终确定为馈线的5个光伏典型日场景矩阵。由图4可以提取出负荷候选典型场景矩阵6个(记为Top1—Top6)，经过Waserstein距离指标筛选后最终确定为馈线的6个负荷典型日场景矩阵。

图5和图6分别为所提取的该馈线全节点光伏、负荷概率最大的典型日场景1曲面图。使用平滑的曲面将矩阵列数(节点编号)形成的曲线相连，能更直观地看出整个场景描述矩阵中各点之间的关联性。在投影到二维平面后能直观看出各光伏、负荷节点在哪些时间点普遍出力较多或较少等情况，更适合规划人员对整个配电网运行场景的全面把控。

图5 该馈线全节点光伏典型日场景1曲面图Fig.5 Surface diagram of full feeder nodes in typical PV daily scenario 1

图6 该馈线全节点负荷典型日场景1曲面图Fig.6 Surface diagram of full feeder nodes in typical load daily scenario 1

由图5可以看出，该馈线某个典型场景的节点在10—15时段光伏出力最大最集中，且由于第3列(5号节点)光伏装机容量最大，其光伏出力值最大。由图6可以看出，该典型场景下负荷节点用电高峰期也集中于10—15时段，与光伏出力高峰期接近。由图4得到的全年6个负荷典型场景得知，每个负荷节点的最高峰时期也基本在9—17时段，基本与全年5个光伏典型日场景的出力高峰重合，可知该馈线有更高的运行稳定性。

3.2 不同方法生成的典型日曲线对比

为了突出本文方法识别典型场景的优点，利用广东某城市配电网数据组成的日场景矩阵，对比使用本文基于LE-GMM的典型场景提取法、k-means聚类法和拉丁超立方采样法生成的典型场景与实际运行场景，结果表明本文方法速度最快，误差最小，更贴近实际运行场景。

对于上述含有10个负荷节点且其中4个包含光伏出力的中压馈线，使用这3种方法得到的典型日场景与馈线后续2个月内实际日运行场景拟合度对比的误差曲线如图7、图8所示。其中k-means聚类方法使用手肘法得到的光伏典型场景最佳聚类数为7，负荷典型场景最佳聚类数为11；拉丁超立方采样得到的光伏、负荷典型日场景数分别为10和11。对整个配电网所有节点全年数据进行典型场景生成，3种方法所使用的时间和误差见表2。

表2 不同方法生成典型场景对比Tab.2 Comparisons of generating typical scenarios using different methods

图7 馈线全节点光伏典型场景误差曲线Fig.7 Typical PV scenario error curves of feeder full nodes

图8 馈线全节点负荷典型场景误差曲线Fig.8 Typical load scenario error curves of feeder full nodes

从表2可以看出，在对整个配电网所有台区光伏和负荷典型场景提取上本文方法所用时间最短，平均误差最小，生成的场景个数更少，能达到更好的效果。

选取最能拟合配电网或馈线各节点真实运行场景的典型场景法，才能准确地为配电网的短期运行调度、发电计划调整以及规划优化等提供可靠参考，这样才具有典型场景生成的现实意义。

4 结论

a)k-means聚类方法的核心是用欧氏距离衡量数据对象间的相似度，对数据进行类别划分并找出聚类中心。但在本文构造的日运行场景描述矩阵中，若只简单使用欧氏距离来衡量矩阵中各行或各列数值之间的欧氏距离，则无法很好地考虑光伏出力时序相关性和空间相关性。采用本文所提LE-GMM算法在矩阵降维时则不仅考虑了矩阵内部数值之间的局部相关性，也保留了矩阵的流行结构，即同时考虑了各节点之间时序以及空间上的相关性，对于所构造的日场景描述矩阵，其识别典型场景的能力较好。

b)拉丁超立方采样方法是一种从多元参数分布中近似随机抽样的方法。根据数据集的分布划分采样区间，确保仅有少量数据的区间也能参与采样。对于一整年的日场景描述矩阵数据集，虽然此方法同样能识别数据集中具有代表性的场景，但受少量极端场景影响，提取的典型场景代表性不强；所以该方法在实际运用中的误差也是最大的。而本文的LE-GMM算法能通过概率密度曲线很好地体现各种场景出现概率的大小，由此判断场景是否具备代表性。

综上所述，相较于传统的k-means聚类算法以及拉丁超立方采样形成的典型场景，本文提出的LE-GMM典型日场景提取算法对实际运行场景有更好的拟合能力，误差更小。搭配所构建的日场景描述矩阵，本文方法能够快速生成整个配电网或整条馈线各个台区节点的典型场景，在得到能高度拟合现实配电网的典型运行场景后，可以为含光伏的配电网运行调度以及发电计划的安排提供可靠参考。