住宅新风系统卧式分风箱风量平衡的研究

周智勇 张俊皓 李佳宜 李定霜

（昆明理工大学建筑工程学院，云南昆明 650500）

0 引言

近年来，越来越多的高品质住宅开始使用集中空调通风系统［1］，在住宅集中通风系统的末端构件中，常常采用新风分风箱来保证各个房间的风量，新风分风箱具有低噪音、把动压转变为静压等优势，但随着室内人员对舒适性和新风量的要求越来越高，为了提高新风分风箱均匀分配风量的性能，现有研究人员对风量分配装置的均匀送风研究如下：江世焕［2］通过试验的方法，使旋流通过风量分配装置，实现在圆形风管上均匀布置的出风口的出风量相等，在风管长度为5D，风口间距为4D时，入口风速为5～12 m/s范围内能够实现风量自动平衡；郑庆红等［3］研究了用于等截面圆形直管均匀送风的旋流风量分配器，通过试验得出了局部阻力静压系数为0.23～0.39 的旋转流量分配器，比国外的降低了75%～69%，针对其特点给出了不同流量下的单位摩擦阻力变化曲线，为工程应用提供了参考依据；王琦等［4］通过CFD 数值模拟和实验验证的方法，分析了风量分配器的进、出风管的不同截面尺寸和风速、导流板的设置位置、长度、角度和不同外接阻力对风量分配的影响情况，为风量分配装置的设计提供了一定的理论依据；常悦等［5］通过CFD 数值模拟的方法研究了体积较小且带有6 个出口的风量分配装置，在不同位置设置不同长度的导流板，可以实现在一定风量范围内使得风量分配器达到风量平衡且各个出口压力相等；张姝雅等［6］通过CFD 数值模拟的方法研究在风量分配装置中设置的导流板高度、角度对风量分配的影响，认为导流板的高度对风量分配的影响较导流板的角度较弱，当导流板的高度为120 mm时，通过调节导流板的角度可以实现一定风量范围内的调节。

以上研究表明优化风量分配器的结构以及在风量分配器中增设导流板，通过改变导流板的角度、位置、长度、高度等可实现风量的调节，但是以上研究所采用的研究方法时间成本高、研究内容不够全面。基于此本文采用CFD 数值模拟结合SPSS 正交实验的方法，将卧式分风箱的导流板结构参数设计作为变量因子、卧式分风箱每个出风口的风量的不平衡率作为因变量，以综合评分为基础作为衡量卧式分风箱各出口风量平衡的指标。设计多种导流板的结构模型并进行流场分析，对仿真结果做极差分析，最终得到卧式分风箱风量平衡最好的一组导流板的结构参数。

1 模型及计算方法

1.1 物理模型及简化

研究对象为某工程住宅新风系统的卧式分风箱，该工程住宅区域相比于其他建筑物，其层高低，根据我国《住宅设计规范》中规定：居住建筑层高为2.8 m，卧室、客厅不得小于2.4 m，且该工程住宅房间顶部铺设有采暖所需要的水管，采取一般通风系统使用的安装方式较为困难，因此该工程采用地板送风的形式并且创新使用了卧式分风箱。

该卧式分风箱基本尺寸为：900 mm×500 mm×60 mm，进风口1 个，进风口风管长度为100 mm，进风口尺寸为：300 mm×100 mm；出风口有8 个，正对面2 个出风口、侧面各3 个出风口，出风口中心距箱体顶面30 mm，出风口风管长度为1 000 mm，出风口尺寸为：130 mm×30 mm，为方便后文的叙述对出风口进行编号，以x轴逆时针方向依次为：出风口1、出风口2、出风口3、出风口4、出风口5、出风口6、出风口7、出风口8，其物理模型如图1 所示。

图1 卧式分风箱外观示意

1.2 数学模型

采用Realieablek-模型及压力与速度耦合的SIMPLE 算法求解其中湍流动能k和湍流耗散率的控制方程分别为：

为简化数值计算，对卧式分风箱内的空气流动作以下假设：

（1）卧式分风箱体内及风管内的空气流速较低，可视为不可压缩流体，流体密度符合Boussinesq 假设。

（2）空气流动为稳态等温流动。

（3）卧式分风箱及其风管的气密性良好，不考虑漏风。

（4）入口风速垂直于入口面，且风速等值分布。

1.3 边界条件

以卧式分风箱进风口为计算入口边界，设为速度入口，大小为2.04 m/s，方向垂直于入口边界面；以风管末端的出口为计算出口边界，设为压力出口，0 Pa。

1.4 网格划分及独立性验证

为保证计算精度的要求，模型采用Fluent meshing进行四面体非结构性网格划分，对卧式分风箱速度入口、风管末端的出口、风管与箱体连接的部分区域的网格进行部分加密处理，如图2 所示。

在送风速度为2.04 m/s 的边界条件下，分别采用表1 中4 种方案精度的网格进行计算，选取卧式分风箱各出风口的风速值来进行网格独立性的验证。由图3 可知，不同网格数量下各个出风口的风速值变化不大，风箱两侧的风速随着网格数量的增加而减小，风箱正对面的2 个出风口的风速随网格数量的增加而增大，观察网格数量为103 万和179 万的出风口风速值变化基本一致，网格数量为333 万时计算精度提高，但造成了计算机计算资源的浪费。因此，可认为从网格数量为103 万开始网格数量已经满足计算的要求，实现了网格的独立性，综合考虑到179 万的网格数所需要的计算资源相对较少，其计算精度已经较高，在进行模拟研究时选取179 万的网格数作为计算网格。

图3 网格数量对出风口风速的影响

1.5 数值模型验证

选择转速为2 380 r/min、静压为180 Pa、送风量为220 m3/h的风机进行模型验证，实测与模拟得出的各个出风口的风速如图4 所示。由图4 可知，模拟得出的各个出风口的风速值变化趋势与实际测试得出的数据的一致性很好，且风箱各个出风口模拟得出的风速与实测风速之间的误差在4.2%～11.9%。因此，数值模型可以用来研究卧式分风箱的风量平衡。

2 正交试验方案设计

正交试验是一种研究多因素、多水平的高效率试验方法，它根据全面试验挑选出具有代表性的案例进行试验，实现各个因素间的均衡搭配，减少实验次数。这些被选出的案例具有“均匀分散，齐整可比”的特点，能全面地反应各个因素水平对试验指标的影响情况［7］。

在卧式分风箱内加装导流板已经证明能够改善风箱内部流场的分布，但导流板的具体结构形式的选择对气流的分布影响较大，为此，采用正交试验方法来探究导流板的各个参数的影响情况并获得最佳的导流板结构参数组合。

2.1 确定评判指标

针对卧式分风箱风量平衡的评判，文中引入不平衡率X作为评判指标。在Fluent 中计算出卧式分风箱每个出风口的平均风速，根据下式计算卧式分风箱各个出风口风速的不平衡率［8］。

式中，X为出风口的不平衡率；Ga为实际出风量；Gd为设计出风量。

不平衡率X的值越小，说明卧式分风箱的各出风口的风量趋于一致，卧式分风箱的风量越平衡。为了使模拟结果全面反映卧式分风箱的风量平衡，本文将各个出风口的不平衡率视做评价指标，由于卧式分风箱的模型是对称的，将出风口1 和出风口8 的不平衡率视作指标a、出风口2 和出风口7 的不平衡率视作指标b、出风口3 和出风口6 的不平衡率视作指标c、将出风口4 和出风口5 的不平衡率视作指标d。

引入综合评分法，综合评分是一种将多指标按着一定的规则转换为单指标的方法。具体来讲，它是综合比较各种指标的重要性及其实测值，对每组试验结果评定出一个综合分数，而以此分数作为单指标进行统计分析。

简单公式评分法是综合评分中的一种方法，当各指标的重要程度和量纲均相同时可以将各指标数值直接相加，然后作为单指标进行分析。文中因指标a、指标b、指标c、指标d 对卧式分风箱风量平衡的判断重要程度相同，因此后文采用简单公式评分得出的综合分数对卧式分风箱的风量平衡进行综合评判。

2.2 正交试验因素和水平的确定

图5 为正交试验架构图。为提高卧式分风箱的送风均匀性，选取了综合评分指标进行评判。对导流片的结构设计选择导流板的长度（因素A）、导流板的高度（因素B）、导流板的夹角（因素C）3 个因素进行正交实验，在每个因素选取3 个水平。导流板的长度的3 个水平为：160 mm、180 mm、200 mm；导流板的高度的3 个水平为：45 mm、50 mm、55 mm；导流板夹角的3 个水平为：65°、75°、85°。导流板的具体结构设计如图6 所示。

图5 正交试验架构

图6 导流板布置模型平面示意(单位：mm）

2.3 设计正交实验表

根据正交试验原理，采用3 因素3 水平L9（33）的正交试验方案来研究不同因素对综合评分的影响，一共需要进行9 组试验，大幅度减少了工作量，提高了试验效率。正交试验方案如表2 所示。

表2 正交试验方案

由表2 可知，设计的试验方案在实验参数的每一列，3 个水平出现的次数相同，且任意2 列的排列方式均衡齐全，充分保证了挑选出的部分试验方案包含所有因素的所有水平，而且任意2 列之间的因素组合全部出现，充分保证了3 个因素之间的组合完整，因此该正交试验的9 组试验方案具有“均匀分散、整齐可比”的特点，可以代表全部试验。

2.4 极差分析

极差可以直观表达出导流板长度、导流板高度、导流板夹角对卧式分风箱风量平衡影响的重要次序，因素的极差越小，表明该因素对送风均匀性影响越小，反之，因素的极差越大，表明该因素对送风均匀性影响越大。极差数学计算公式为：

式中，kj为因素X的j水平对应的指标和；Xj（i）为因素X的第j水平第i个因素组合方案所对应的实验值。

式中，kj为因素X的第j个水平的和的均值。

式中，R（X）为X的极差；Max（kj）为因素X的第j个水平和均值中的最大值；Min（kj）为因素X的第j个水平和均值中的最小值。

通过表3 极差分析可知，3 个因素对综合评分的影响程度不同，根据表中极差值的大小可以判断影响因素的主次顺序为：导流板高度＞导流板角度＞导流板长度。为更加直观地显示3 个因素水平对综合评分的影响，以3 个因素的水平为横坐标，以综合评分为纵坐标得到如图7 所示的正交分析指标图。

表3 试验结果的极差分析

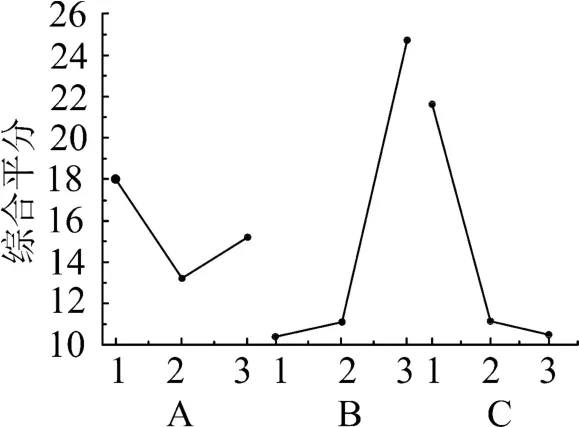
图7 正交分析指标

由正交分析指标图可得，3 个因素试验水平实验7 的综合评分最低，即导流板结构参数设置效果最好的是导流板长度为200 mm、导流板高度为45 mm、导流板角度为75°。

2.5 结果验证分析

通过正交试验结果分析得到了送风均匀性较好的导流板结构参数，为验证试验结果，根据优化后的试验参数建立模型，在相同的边界参数下进行数值模拟，得到的结果如表4 所示。

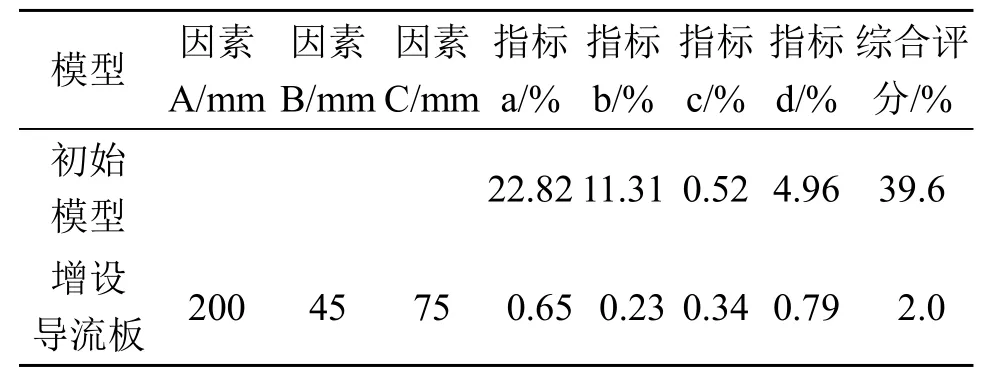
表4 试验结果验证对比

从表4 可以看出，初始模型卧式分风箱风量平衡的综合评分为39.6%，增设导流板优化后卧式分风箱风量平衡的综合评分为2%，较初始模型综合评分降低37.6%，说明卧式分风箱风量平衡提高37.6%。

3 结论

为了研究卧式分风箱风量平衡的问题，本文从卧式分风箱的物理模型入手，采用CFD 数值模拟和SPSS正交试验相互结合的方法，以综合评分为指标，对卧式分风箱内设置导流板的结构参数进行了优化分析，最终得出以下结论：

（1）导流板结构参数中3 个试验因素对于卧式分风箱风量平衡影响的主次顺序为：导流板高度＞导流板角度＞导流板长度。

（2）导流板结构参数对卧式分风箱风量平衡影响效果最好的是：导流板长度为200 mm、导流板高度为45 mm、导流板夹角为75°。

（3）基于正交试验优选的导流板结构参数组合，对卧式分风箱风量平衡进行仿真验证。结果表明：优化设置导流板后的模型比初始模型各支路的不平衡率降低了37.6%，送风均匀性整体提高。

本研究将室内实验与理论研究相结合，为未来卧式分风箱的优化设计提供参考。对于卧式分风箱设置导流板来调整风量分配有一定的理论依据，但是应用到实际工程中存在一定的局限性，因此在未来的研究中，将针对工程实际情况与本模型结合并加以修正，对卧式分风箱的认识会更加准确。