基于自适应分段云模型的电力异构数据聚类研究

孙 妍,张俊超,马占海,严嘉正

(国网青海省电力公司信息通信公司,青海 西宁 810008)

0 引言

随着智能电网的广泛使用,电网的智能化水平正在逐步提升,使得电网中的各类数据可以进行聚类[1]。云计算技术在电网中的广泛运用,使得电网中的信息系统复杂化程度不断降低。但是,随着电力网络异构数据的增加,为保证云计算网络中电网的安全、稳定,需要对异构数据进行聚类,从而有效地排除异构无关冗余数据[2-3]。由于云计算模式下电力异构数据具有种类繁多、数据维度大、结构复杂的特点,所以电力异构数据聚类多为自适应分段式聚合[4]。对此,相关学者进行了研究。

庞传军等[5]提出基于长短期记忆(long short-term memory,LSTM)网络的电力负荷聚类建模及特性分析方法。该方法采用LSTM自动编码器提取负荷数据特征,采用k-means算法完成电力负荷数据聚类分析。该方法聚类精度较高,但是数据聚类较慢。梁京章等[6]提出基于核主成分分析(kernel principal component analysis,KPCA)和改进k-means的电力负荷曲线聚类方法。该方法将密度聚类思想结合k-means算法,以实现数据快速降维聚类。该方法数据聚类能力较强,但是容易产生冗余数据。Guleria K等[7]提出1种增强能量以降低传感器节点分簇能量消耗的方法。该方法根据移动节点从固定节点中选择簇头,传输移动节点数据;利用粒子适应值计算继节点的速度和位置,完成电力节点链路故障预测,提高网络寿命。但是该方法的计算算力有待验证。Kannan N等[8]利用远程处理技术构建电力系统实时监控组件模型,以提高系统的可重用性和可扩展性。该方法使用具有公共对象请求协议的架构开发潮流监控模型,以解决实时经济负荷调度和动态安全监控;结合潮流监测、动态安全监测和经济负荷分配,优化分布式平台体系结构,从而实现对电力系统的性能监测。但是该方法在复杂电网环境下的聚类收敛效果仍需进一步提升。

云模型由隶属云与语言原子模型演化而成,采用数字特征描述具有定性概念特点的定量数值,可有效减少冗余数据。云模型通过不确定性转化提高数据聚类速率,进而有效提升数据聚类效果。基于此,本文应用自适应分段云模型,采用Tent映射电力异构数据,通过云期望曲线方程计算数据聚类中心,利用熵值完成有序聚类。仿真测试结果表明,本文提出的基于自适应分段云模型的电力异构数据聚类方法的漂移基本特征聚类效果较优、分类聚类面积较大、聚类收敛效果较好、轮廓系数数值较高,能为电力系统的安全、稳定运行提供技术支持。本文研究对目前电力行业的异构数据处理进行了探讨,对预测电力系统的发展趋势具有重要意义。

1 基于Tent映射的电力异构数据预处理

电力系统包含发电、变电、输电、配电等逻辑结构,所以电力数据具有多源异构的特点。同时,由于电力系统数据在云空间的分布较为分散,电力异构数据无法有效聚类,从而降低了数据聚类精度。Tent映射属于混沌系统中的一种分段式线性函数[9]。利用拓扑共轭映射关系使数据空间分布均匀,可提高聚类寻优效率和求解精度。Tent映射的数学表达式为:

(1)

式中:zi为电力异构数据种群初始值;0<α<1。

本文将电力异构数据种群初始值转化到数据个体搜索空间,建立Tent混沌映射序列,以完善数据遍历。

(2)

式中:N为异构数据总量,MB;φi为种群规模;q为空间维数;Sm为元素数组;m为期望的类簇个数。

在有限维数据内积空间内,本文设定拓扑共轭映射关系,划分异构数据数组:

(3)

式中:wij为数据空间中相同簇的i和j之间的距离。

本文将异构数据进行Z-score标准化[10],以扩大元素数组的组内相似性和组间差距,使数据空间分布均匀:

(4)

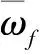
通过Tent映射的方式均匀数据空间分布,可以提高聚类寻优效率和求解精度,完成数据聚类预处理。

2 基于自适应正态云模型的数据聚类中心确定

正态云模型可以清晰展现Tent混沌映射关联,确保数据空间内的电力异构数据元素数组的完整性和一致性。本文假设W为论域、E为论域上的定性概念。当定量值x∈W时,x对E的隶属度函数为:

(5)

式中:ti为迭代时间,s;x0为簇首节点半径处于隶属度函数第一象限的概率[11];xi为簇首节点半径处于隶属度函数无效象限的概率。

通过隶属度函数获取稳定倾向随机值后,本文使用正态云模型的期望值Fx、熵值Fn和超熵值Hf这3个数字特征,建立云期望曲线方程[12]。其中:Fx为定性概念中最具代表性的指标;Fn为定性理论模糊度衡量标准;Hf为期望值Fx的不确定性度量。

本文通过Fx和Fn确定电力异构数据元素数组的云期望曲线方程:

(6)

式中:n为正态云滴。

由于正态云模型是由x个正态云滴构成,需要对云滴性质进行判定。其详细步骤如下。

③推算随机值λ对E的隶属度,以获取论域内正态云滴性质。

(7)

式中:γ为隶属度系数。

④反复执行步骤①～步骤③,直至获取正态云模型中的所有正态云滴。

本文根据正态云滴性质对电力异构数据元素数组实施云化处理,并根据有限维电力异构数据元素数组中心向量确定数据聚类中心。

(8)

式中:σ为可能性划分系数;l为电力异构数据元素数组到聚类中心的距离;vi为电力异构数据元素数组中心向量。

通过正态云模型中的期望值、熵值、超熵值获取论域内正态云滴性质,可确定数据聚类中心,为后续有序聚类提供支持。

3 基于熵值的异构数据有序聚类

本文根据正态云模型的熵值评价Tent混沌映射序列异构数据稳定性、定义子序列分段条件,以提高分段聚合的有效性。本文设子序列为D(i0,j0),在数据聚类中心计算正态云模型最大熵值:

(9)

式中:T′j为Tent混沌映射序列在固定时间下的关键节点j的边界域。

本文利用目标函数剔除最大熵值下的异构数据元素数组,以消除无关、冗余数据,使目标函数值达到最小。

(10)

式中:pi为离散随机变量;φ为模糊加权指数。

本文在优化后的异构数据元素数组中定义分段聚合条件,并以pi作为异构数据相似度。异构数据元素的权重为:

(11)

本文根据di划分异构数据聚类数组,创建di的权重熵元素数组Di;利用云分段聚合近似算法,对Di进行分段。

(12)

式中:lj为Tent混沌映射序列最大概率;li为对应的异构数据类簇特征状态。

本文利用正态云模型描述异构数据在云分段聚合状态下的聚类收敛结果,以完成异构数据有序聚类。电力异构数据有序聚类流程如图1所示。

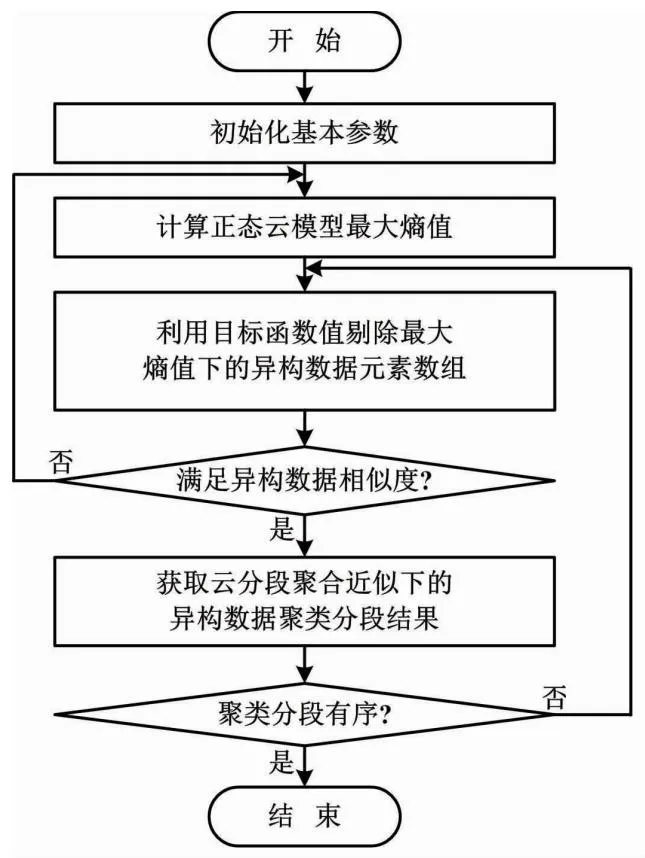
图1 电力异构数据有序聚类流程图

基于图1所示流程,本文完成了电力异构数据有序聚类,有效解决了鲁棒性问题,实现了基于自适应分段云模型的电力异构数据聚类方法的设计。

4 仿真测试

4.1 仿真环境

为了验证基于自适应分段云模型的电力异构数据聚类方法的整体有效性,仿真测试在国网某公司信息通信数据库中随机选取2022年上半年的1 000组异构数据。其中:600组异构数据用于训练;400组异构数据用于仿真测试。仿真测试利用本文方法、文献[5]方法、文献[6]方法,从漂移基本特征聚类、分类聚类面积、聚类收敛效果等方面进行对比分析。仿真测试平台为Matlab R2022a。仿真测试分析在主频为1 Hz的环境下完成。

4.2 仿真结果与分析

4.2.1 漂移基本特征聚类分析

训练集在模拟聚类过程中存在异构数据点密集区域选取不当的情况,容易造成训练集过拟合。因此,为了提高训练样本聚类均衡度,需要对异构数据聚集程度进行优化。仿真以漂移基本特征聚类作为测试内容,使用单个滑动窗口进行聚类拟合;以数据空间分布均匀、滑动窗口移动方向与漂移基本特征聚类路径一致为较优的聚类结果。本文对比本文方法、文献[5]方法和文献[6]方法的漂移基本特征聚类效果。漂移基本特征聚类效果越优,则异构数据聚类求解精度越高。漂移基本特征聚类结果对比如图2所示。

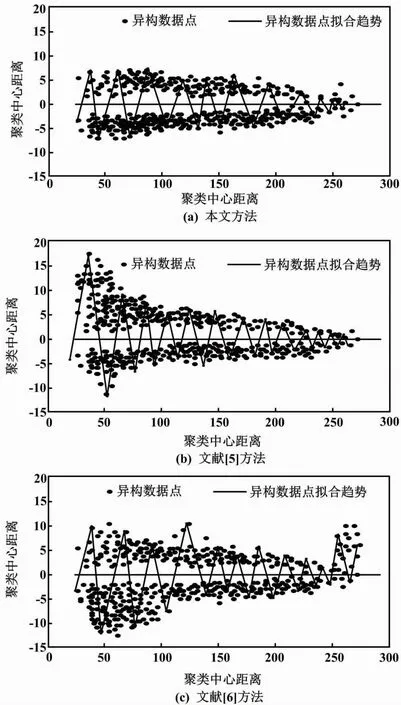
图2 漂移基本特征聚类结果对比

由图2可知,在相同基本特征的异构数据聚类拟合程度下,本文方法的数据空间分布较为均匀,且滑动窗口移动方向与漂移基本特征聚类路径一致。而文献[5]方法和文献[6]方法的数据空间分布存在失衡,所得的异构数据漂移基本特征聚类过于杂乱。由此说明,本文方法异构数据聚类求解精度较好。这是因为本文方法采用Tent映射对电力异构数据进行聚类预处理。预处理后的异构数据不均衡性得到降低,进而使数据空间分布均匀,漂移基本特征聚类能力得以提高。

4.2.2 分类聚类面积分析

样本项之间的相似度越高,则数据聚类效果越好。在相同基本特征的异构数据聚类拟合程度下将期望曲线相交,得到异构数据分类聚类面积,并根据样本特征出现概率衡量聚类效果。分类聚类面积越大,则表明样本项之间的相似度越高,且能有效减少无关、冗余数据,完成异构数据聚类。分类聚类面积结果对比如图3所示。

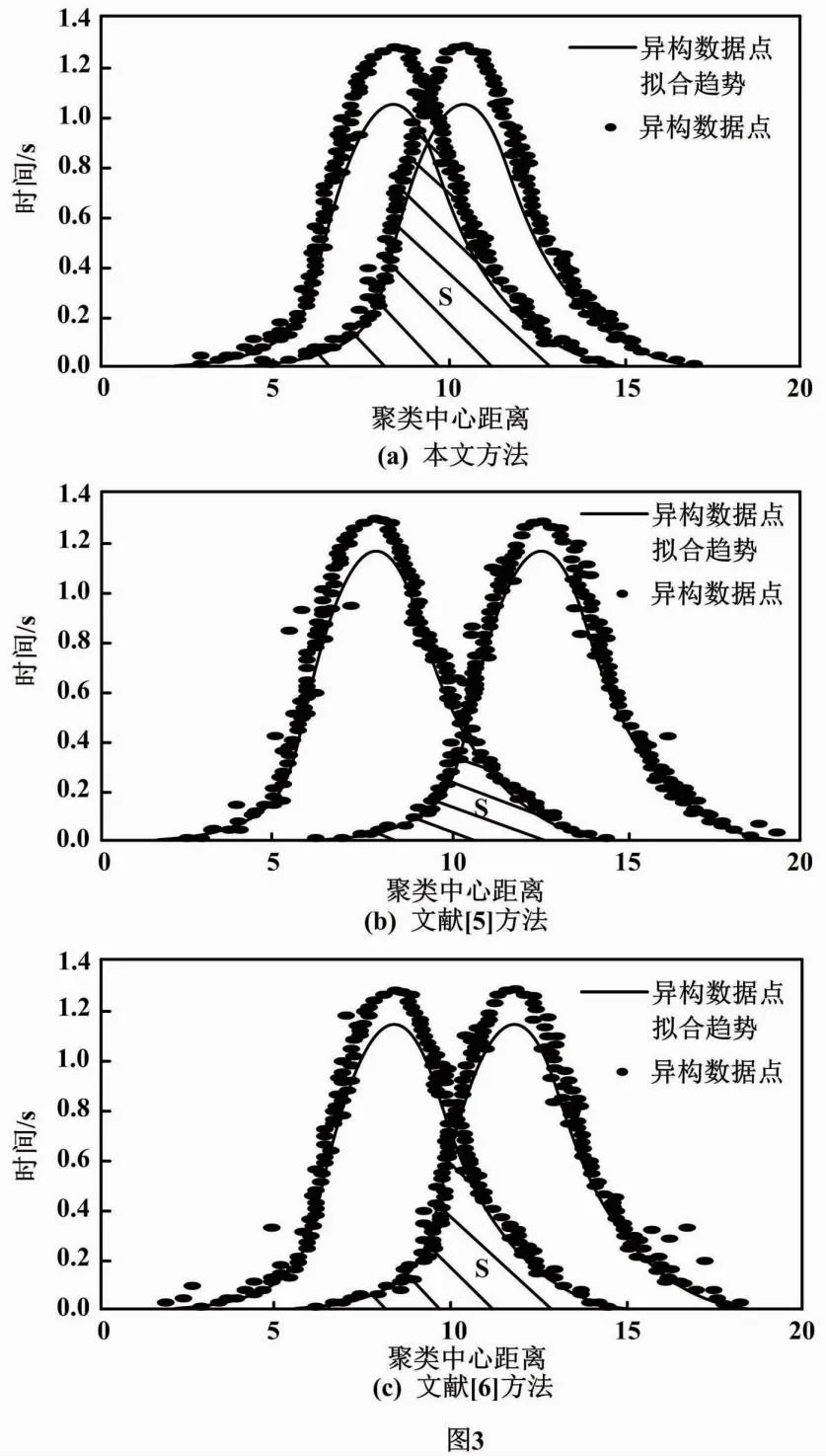
图3 分类聚类面积结果对比

由图3可知,本文方法分类聚类面积(图中S处)大于文献[5]方法和文献[6]方法,且异构数据聚类拟合效果较优。这是因为本文方法通过云期望曲线方程获取了论域内正态云滴性质、确定了异构数据聚类中心,进而提升了期望曲线相交效果、扩大了分类聚类面积,从而有效完成了异构数据聚类。

4.2.3 聚类收敛曲线分析

基准测试函数可以测试算法在固定聚类负载下的性能。本文设定迭代次数为1 000次,以获取目标函数平均收敛曲线。通过分析本文方法、文献[5]方法和文献[6]方法的目标函数收敛曲线,验证本文方法的收敛性能。聚类收敛结果对比如图4所示。

图4 聚类收敛结果对比

由图4可知,在迭代开始时,本文方法的收敛曲线快速下降。这是因为Tent映射预处理了异构数据,有效提高了算法的收敛速度。而文献[5]方法和文献[6]方法陷入停滞的次数高于本文方法。随着迭代次数增加,本文方法能够迅速跳出局部最优,并且可以较快地完成异构数据聚类。这是因为本文方法利用云分段聚合近似算法对异构数据聚类权重熵元素数组进行分类,有效提高了聚类的有序性,进而提升聚类收敛效果。

4.2.4 轮廓系数分析

轮廓系数是评价聚类效果的1种指标,可以在相同原始数据的基础上评价不同方法对聚类结果产生的影响。轮廓系数的计算式为:

(13)

式中:a(k)为数据节点k到所有其属于的簇中其他点的距离;b(k)为数据节点k到与其相邻最近一簇内的全部点的平均距离。

轮廓系数值介于[-1,1],越趋近1代表聚类效果越好。测试样本为400组用于测试的异构数据。数据以每100组为1个组别,共4个组别。不同方法的轮廓系数对比如表1所示。

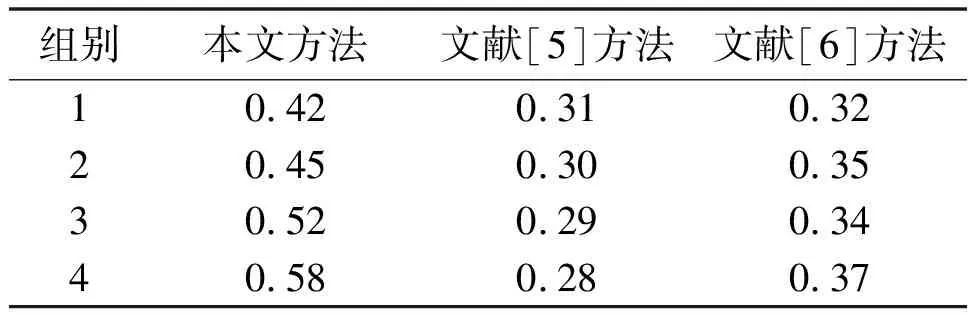
表1 不同方法的轮廓系数对比

由表1可知,在聚类电力异构数据时,本文方法轮廓系数能保持在0.4以上;文献[5]方法和文献[6]方法的轮廓系数均在0.4以下。这说明本文方法的聚类效果较优,在聚类过程中充分考虑了电力异构数据的整体信息,可以正确分割类簇。

5 结论

为了提高云计算环境下电力系统运行的安全性和稳定性,本文提出基于自适应分段云模型的电力异构数据聚类方法。该方法通过引入自适应正态云模型,均匀异构数据空间分布、确定数据聚类中心,以实现异构数据有序聚类。仿真测试结果表明,本文方法在保证数据聚类速率和减少无关、冗余数据的基础上,漂移基本特征聚类效果较优、分类聚类面积较大、聚类收敛效果较好、轮廓系数数值较高。这证明本文方法具有较强的聚类效果,可以为电力异构数据聚类系统设计提供理论支持。但在实际应用中,异构数据中也可能存在部分先验信息。后续研究将考虑利用先验信息进一步提高电力异构数据聚类性能。