复杂异型建筑立面测绘轮廓提取方法设计
于 淮,张 燕
(1.广西工业职业技术学院建筑工程学院,广西 南宁 530000;2.桂林理工大学南宁分校,广西 扶绥 532100)
0 引言
目前,针对常规建筑立面测绘轮廓提取的研究很多[1-2],但针对复杂异形建筑立面测绘轮廓信息提取的研究极为匮乏。分析已有的常规建筑立面测绘轮廓提取资料可知,文献[3]方法使用α-shape算法提取建筑立面测绘轮廓点数据后,以轮廓点筛选的方式获取关键轮廓点组建为轮廓线。但激光脉冲扫描速度、建筑物反射光会影响立面测绘时点云数据的密度信息。如果直接使用α-shape算法提取轮廓点的点云数据,并不能保证提取数据的准确性。文献[4]方法使用Shi-Tomasi算法提取建筑物立面测绘轮廓。该算法能够以轮廓和轴线的最优拟合方式提高轮廓提取精度,但仅对矩形建筑具备较好的轮廓提取效果,使用范围有限。
本文结合前人研究成果以及所分析的应用局限,提出一种基于局部点云密度的复杂异型建筑立面测绘轮廓提取方法。Alpha Shapes算法属于多形态点云轮廓线提取算法,具有操作难度小、鲁棒性显著的特点。该算法可以自适应调节滚动圆半径,优化轮廓提取效果;通过点云数据平滑、分割两种预处理方式,有效优化复杂异型建筑立面测绘时的点云数据质量。此外,该算法还能够以分割的方式有效锁定测绘图像中的目标点云区域,从而提升测绘轮廓提取精度。
1 复杂异型建筑立面测绘轮廓提取方法
1.1 测绘点云数据平滑方法
考虑到复杂异形建筑的结构、形状存在差异化特征,本文将复杂异形建筑里立面测绘图像的区域分解为平面区域(无不规则结构过渡区)、次特征区域(存在不规则结构,但结构复杂性较低)与富特征区域(存在不规则结构,且结构复杂性显著)。平面区域采取平面拟合投影方法,将正交投影点设成平滑后点。对次特征和富特征区域而言,为防止多次曲面拟合导致计算量增加,本文使用变参数双边滤波方法完成平滑去噪。
1.1.1 平面区域
平面区域无不规则结构,所以曲率变化不大。为此,本文使用正交投影点代替此区域的原始点云数据点,完成点云数据去噪平滑[5-7]。在设置复杂异形建筑立面测绘图像中,某点云数据的投影点是q″(x″,y″,z″)。
(1)
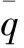
1.1.2 次特征与富特征区域平滑
双边滤波算法操作难度小,且应用效率显著[8],在平滑次特征与富特征区域时不会破坏点云数据的几何特征。而复杂异形建筑立面测绘图像的几何特征较为复杂[9-10],只使用双边滤波方法平滑点云数据时并不能保证次特征、富特征区域的特征不出现失真问题。为此,本文采用变参数双边滤波方法完成此区域的点云数据平滑。
q‴=VcVs(q-βm)
(2)
式中:q‴为平滑后的点云数据点,其坐标为(x‴,y‴,z‴);Vc为平滑滤波;Vs为特征保持的权函数;β为双边滤波因子。
变参数双边滤波方法主要控制原始点云数据点q朝自身法向位置移动,以完成平滑滤波。
β=〈q-qi,m〉
(3)
式中:〈q-qi,m〉为平滑滤波向量的内积值;qi为q的邻域点。
(4)
式中:e为自然常数;αc为高斯滤波系数;x为点云数据三维初始横坐标点。
(5)
式中:αs为高斯权值带宽;y为点云数据三维初始纵坐标点。
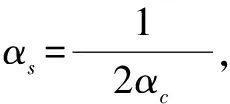
综上所述,本文将两种区域平滑后的点云数据统一设为′q。
1.2 点云分割方法
针对1.1节平滑后的点云数据,本文使用d维平衡二叉树组织测绘点云数据,并从X、Y、Z方向执行剖分处理。处理后复杂异形建筑立面测绘图像中,点云数据平面和相应的轴向存在垂直关系。当全部点云数据结构都处于二叉树后便可停止。本文将点云数据所在二叉树设成d维欧式空间Sd。Sd中的全部点云数据向量均以相互正交的方式分布[11]。

(6)
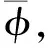
本文设置三维欧式空间S3中点云数据平面为θ:
ξx′+Ψy′+ζz′=θ
(7)
式中:ξ、Ψ、ζ分别为S3空间的平面法向量数值。
若将点云数据平面法向量单位化,便得:
(8)
本文设置S3里随机一个点云数据点qj属于建筑立面测绘的轮廓点数据和目标点云数据,其三维坐标是(xj,yj,zj),j=1,2,…,h。其中,h为S3中点云数据点的数量。qj与最优拟合平面的距离为lj。结合最小二乘法,本文为了有效分割获取qj,需使用其邻域数据点提取最优拟合平面。
(9)
式中:U为点qj至最优拟合平面距离的平方和。
本文结合最优拟合平面信息,设置目标点云分割半径,以执行立面测绘点云数据分割。分割半径r为:
(10)
式中:ρ为目标点云数据点的局部点云密度。
综上所述,使用局部点云密度便可计算分割半径,从而完成复杂异形建筑立面测绘的点云分割、提取目标点云区域。
1.3 立面测绘轮廓提取方法
1.3.1 边界网格筛选
立面测绘轮廓提取方法主要分为目标点云区域的边界网格筛选、轮廓提取这两个步骤。在操作过程中,其主要使用滚动圆完成边界网格筛选。滚动圆半径为目标点云区域边界轮廓提取的核心参数。当半径大于上限标准时,会导致轮廓细节特征检测精度变差,从而影响提取精度;当半径小于下限标准时,会导致提取的轮廓线存在断裂问题。
为优化轮廓提取过程、去除目标点云区域中冗余立面测绘信息中的点云数据点,本文设计目标点云区域的二维网格。
①投影三维点云。
本文将1.2节分割获取的目标点云区域投影到水平面,即可获取投影后目标点云区域的二维点云。
②设计二维网格。
网格密度对目标点云区域边界提取效果存在直接影响。密度较大,会导致轮廓细节失真,使得运算量随之增加。密度较小,则会导致轮廓提取结果中存在孔洞状态。为此,本文需要掌握轮廓的大小,以此调节网格的密度大小。本文使用孔洞大小运算方法,设定孔洞横坐标、纵坐标最大值与最小值分别为(xmax,xmin)、(ymax,ymin),孔洞大小为Fsize,则有:
(11)
式中:γ为网格密度。
本文设置二维网格里′q的初始坐标为(x,y),则′q在网格中的行信息τ和列信息μ分别为:
(12)
(13)
1.3.2 轮廓提取
轮廓提取方法如图1所示。
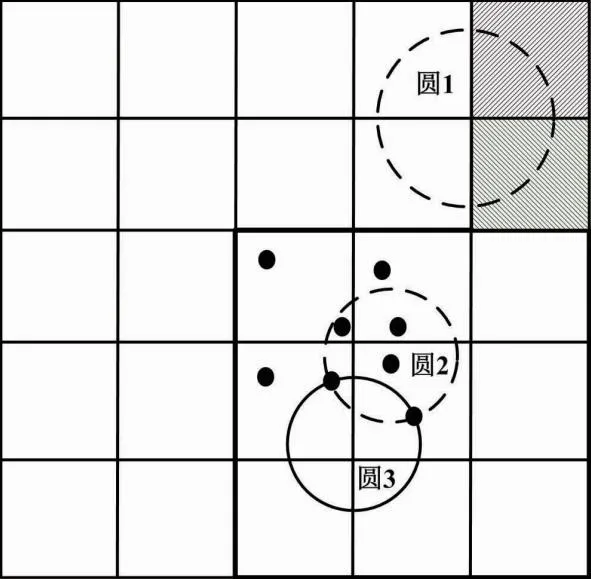
图1 轮廓提取方法示意图
因为二维网格尺寸比点云之间点距均值大,所以直接将边界网格点云设成轮廓点云数据并不准确。为此,本文首先将二维边界网格设为中心,设计3×3网格检测窗口(图1中的加粗黑色线框);然后结合网格平滑种类信息,设定半径差异的滚动圆,用于检测窗口中的点云,从而提取准确的边界轮廓数据点。本文设置二维边界网格集合为δ、初始半径为r′0、滚动圆半径调节系数为η。详细步骤流程如下。
①构建检测网格窗口。

②建立滚动圆。

③提取边界点。

④遍历边界网格,提取边界轮廓。
循环上述操作,便可得到全部边界点对和边界线。输出的全部边界线即立面测绘完整的边界轮廓。
2 试验分析
为测试本文方法对复杂异形建筑立面测绘图像是否具备轮廓提取能力,本文将AS-100无人机激光雷达系统在某市获取的复杂异形建筑测绘图像作为试验数据。此图像结构具有不规则特征,结构上部和下部的形状不一致,属于异形结构。
2.1 点云数据平滑处理效果
平滑前测绘图像点云数据如图2所示。

图2 平滑前测绘图像点云数据图
图2测绘图像因机载LiDAR在采集立面点云数据时存在不规律移动状态,导致点云数据平滑性较差,从而影响测绘图像的成像效果。为此,本文方法使用基于平面投影和双边滤波的测绘点云数据平滑方法。
本文对图2执行点云数据平滑处理。平滑后测绘图像点云数据如图3所示。

图3 平滑后测绘图像点云数据图
对比图2、图3可知,本文方法对图2执行点云数据平滑处理后,点云数据平滑度明显提升。此建筑立面测绘图像画质得以优化。
2.2 建筑立面测绘点云分割效果
本文方法在执行建筑立面测绘点云分割时,以图3中建筑立面整体框架轮廓、窗户轮廓为提取对象,设置φ=0.06。
本文方法在分割建筑立面测绘点云数据时,考虑和未考虑局部点云密度所得建筑立面测绘点云分割效果如图4所示。

图4 建筑立面测绘点云分割效果
图4(a)背景和建筑目标之间点云数据特征混合,且无明显分界线。这会导致点云分割出现过分割问题,使分割误差较大。本文方法考虑局部点云密度,使用局部点云密度计算分割半径,从而有效完成复杂异形建筑立面测绘的点云分割,即如图4(b)所示的分割效果图中不存在过分割问题。
2.3 测绘轮廓提取

测绘轮廓提取结果如图5所示。

图5 测绘轮廓提取结果


(14)
式中:x1、x2、x3依次为提取结果中正确轮廓尺寸、错误轮廓尺寸、遗漏轮廓尺寸。
应用文献[3]方法和文献[4]方法分别提取测绘轮廓,在计算得到两种方法对轮廓的提取精度后将结果与本文方法进行对比。提取的轮廓匹配度结果对比如表1所示。

表1 提取的轮廓匹配度结果对比
由表1可知,文献[3]方法和文献[4]方法提取的复杂异形建筑立面测绘轮廓的匹配度均未达到90%;本文方法提取的复杂异形建筑立面测绘轮廓匹配度为95.08%。因此,本文方法匹配度较高、提取效果更理想。
3 结论
本文对复杂异形建筑立面测绘轮廓提取问题进行深入研究,提出了有效的轮廓提取方法。该方法可作为复杂异形建筑立面测绘轮廓提取方法。但本文方法的提取效果仅适用于试验中单层屋顶的不规则异形建筑。现实中很多建筑屋顶结构更为复杂,如多层不规则屋顶、多层多形状屋顶结构等。后续研究将侧重更为复杂的异形建筑立面测绘轮廓提取问题,通过引入分层屋脊线特征提取,进一步优化本文方法对复杂异形建筑立面测绘轮廓提取的性能。

