变调节因子的不同容量锂电池储能系统能量控制策略

鄢仁武 姜雪儿

变调节因子的不同容量锂电池储能系统能量控制策略

鄢仁武1,2姜雪儿1

（1. 福建理工大学电子电气与物理学院，福州 350118; 2. 智能电网仿真分析与综合控制福建省高校工程研究中心，福州 350118）

为解决不同容量储能单元（ESUs）的荷电状态（SOC）均衡控制与功率分配问题，提出一种变调节因子的不同容量储能系统能量控制策略。通过建立引入容量因子的指数函数，实现各ESU按照其容量比分配输出功率，同时设置动态调节因子，使其随各ESU的SOC与全局SOC平均值差值的减小而增大，解决最大输出功率与均衡速度不可兼顾的问题。为减小通信压力，采用动态一致性算法获取全局平均值，并制定通信故障时的控制策略，使系统稳定运行。最后，进行Matlab/Simulink仿真研究，结果表明所提策略相较于固定调节因子SOC均衡策略具有更快的均衡速度且能实现更精准的功率分配。

锂电池储能系统；能量控制；均衡技术；不同容量

0 引言

随着以光伏为代表的直流微源的广泛应用和不断增加的直流负荷需求，直流微电网正在迅速发展，吸引了越来越多相关学者的关注和研究[1]。直流微电网有两种运行模式：并网模式和孤岛模式。孤岛模式下，直流微电网不依赖外部电力网络，它能够通过本地可再生能源来满足当地负载需求，实现自给自足的电力供应[2-3]。同时，考虑到可再生能源的间歇性和不确定性，独立型直流微电网需要设置锂电池储能系统来平稳管理能量波动，保持系统功率平稳，以及维持直流母线电压稳定[4-5]。随着微电网的功率需求逐渐增加，通常需要将多个储能单元（energy storage unit,ESU）连接到直流母线上，从而形成一个分布式储能系统[6-7]。这种配置可有效增加储能容量和功率输出，以应对更高的电能需求，同时提高微电网的稳定性和可靠性。储能设备的老化、充放电速率差异、温度不均和制造差异会导致储能系统出现荷电状态（state of charge,SOC）不一致现象，而SOC不一致会导致部分储能单元过充和过放，造成能量损失，大大降低其使用寿命[8-10]，因此使用合理的SOC均衡控制策略消除储能单元之间的不一致性对于改善储能系统性能具有重要意义。

为解决不同储能单元之间SOC不一致的问题，文献[11]建立下垂系数与SOC次方的函数关系，其中用于调节均衡速度，越大SOC均衡速度越快；文献[12]将下垂控制中的电压替换成电压变化率，从而减少因线路阻抗而导致的电压电流影响，同时对所提出的下垂控制策略进行了补偿；文献[13]采用一种改进的SOC幂指数下垂控制方法，根据系统SOC快速分配负荷，提高SOC均衡速度；文献[14]在传统下垂控制的基础上增加SOC控制环节，并且带有电压补偿，降低了对系统稳定性的影响；文献[15]设计采用对数形式的基于SOC的参考电压，以所有储能单元的SOC平均值与各储能单元的SOC比例作为输入，实现母线电压无偏移的均衡控制；文献[16]将需要进行最大功率充电或放电的ESU配置为主要ESU，其他ESU则根据主要ESU的SOC变化调整其自身SOC，且进一步减小了母线电压偏差；文献[17]引入等效参考输出电流，通过比例积分（proportional integral, PI）控制器生成电压补偿信号，以提高电流分配的准确性；文献[18]通过建立指数型下垂控制中放大因子与SOC差值之间的函数关系，实现了兼顾功率响应速度和收敛速度。

本文在分析固定调节因子SOC均衡策略后，提出变调节因子的SOC均衡策略，以提高系统的整体收敛速度；同时，引入容量因子，使各个模块的输出功率趋于容量比。此外，采用相邻通信方式来实现分布式储能系统的能量管理，运用动态一致性算法来估计全局平均值信息，以降低通信负担和成本，增强系统的可靠性；考虑到通信故障，提出故障时的SOC控制策略，以保证系统稳定运行。最后，以三组储能单元为对象，对本文所提均衡策略进行仿真研究。

1 独立直流微电网下垂控制策略

一个典型的独立直流微电网结构如图1所示，主要由光伏、风电等可再生新能源、储能系统、负载及变换器组成[19-20]。

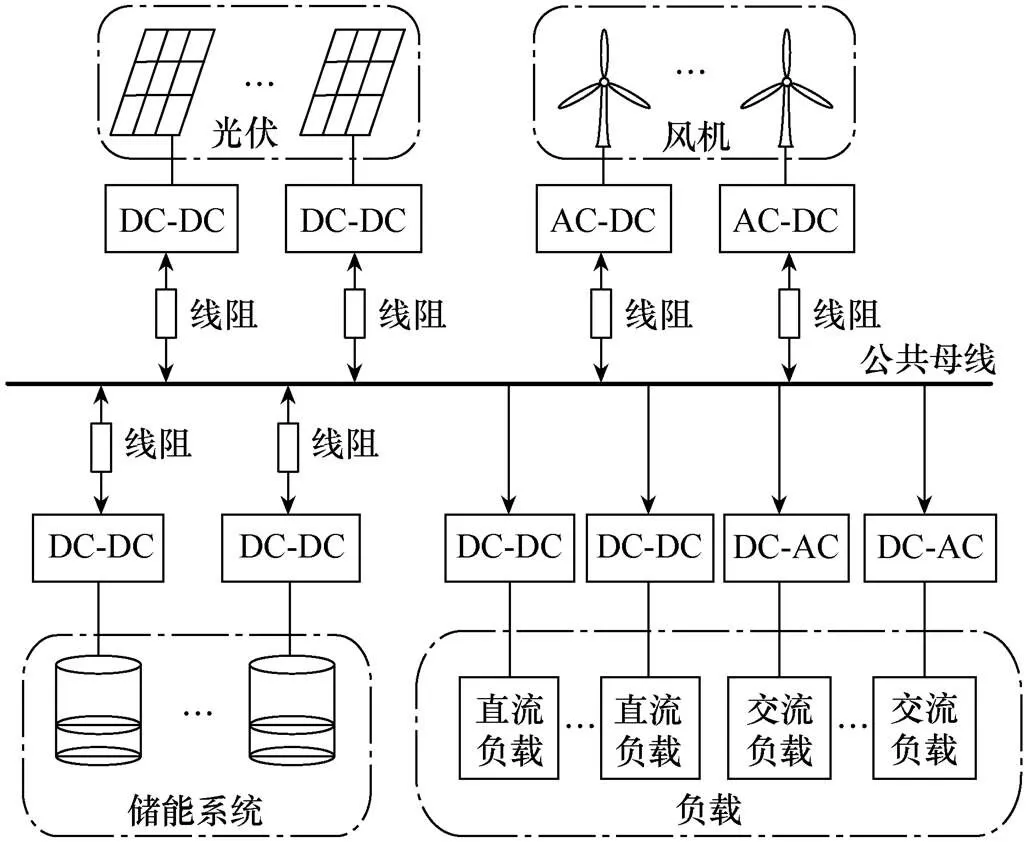
图1 独立直流微电网结构

直流微电网通常采用下垂控制进行ESU之间的能量分配管理。常规的下垂控制表示为

式中：dci、I分别为第个变换器的输出电压和输出电流；R为下垂系数；oi为给定初始电压。

根据式（1）可得到下垂控制特性曲线如图2所示。其中，图2（a）为调整下垂系数时的输出电压电流特性曲线，图2（b）为改变给定初始电压时的输出电压电流特性曲线。由图2可知，在系统运行过程中，可通过这两种方式调整负荷的输出电流[21]。

图2 传统下垂控制特性曲线

一般情况下，储能单元的SOC通过安时积分法进行估算，其表达式为

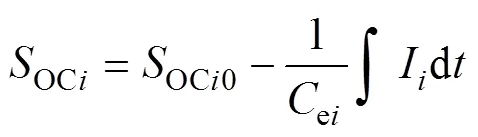
式中：OCi为第台锂电池的荷电状态；OCi0为第台锂电池初始时刻的荷电状态；ei为电池的额定 容量。

以直流微电网中两个分布式储能单元并联运行为例，储能系统等效电路如图3所示。line1和line2分别为两台双向DC-DC变流器输出端口到母线公共点的线路电阻，1和2为虚拟阻抗，即下垂系数；1和2为输出电流；bus为负载电压，load为负载阻抗，dc1、dc2为变流器的输出电压，o1、o2为变流器的给定初始电压。

图3 储能系统等效电路

由于变换器控制策略中包含电压闭环，所以变换器的输出电压跟随给定值，若储能单元的额定容量相同，则两个变换器输出电流的比例关系为

由式（3）可得，变换器的输出电流与下垂系数和线路电阻之和成反比例关系。而传统下垂控制的下垂系数是固定的，未考虑SOC这一变量，因此无法实现不同储能单元之间SOC的均衡，且线路电阻会影响电流的精准分配。

2 固定调节因子SOC均衡策略局限性分析

固定调节因子SOC指数型下垂控制的下垂系数设定为

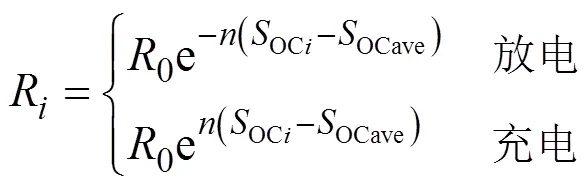
式中：R为储能单元的下垂系数；0为初始下垂系数；为调节因子；OCave为储能系统中各储能单元的SOC平均值。

储能单元的SOC与系统SOC平均值的差值记为DOCi，有

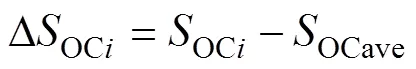
对式（2）进行一阶求导得

在充电模式下，联立式（1）、式（4）和式（6）得

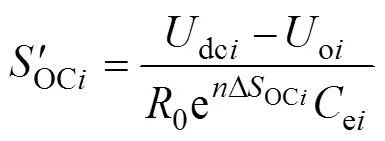
由式（7）可得，SOC的变化率与DOCi、均衡速度调节因子和额定容量ei有关。

以两个额定容量相同的储能单元为例，两个储能单元SOC变化率的比值为

式中，DOC为储能单元1的SOC值与储能单元2的SOC值之间的差值，其表达式为

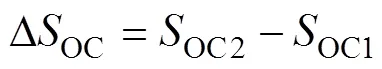
根据式（8），绘制不同调节因子对应的DOC与SOC变化率之间的比值曲线，得到SOC变化率比值与DOC的特性曲线如图4所示。

图4 SOC变化率比值与DSOC的特性曲线

由图4可知，当DOC相同时，SOC变化率之比随着的增大而增大，即越大，SOC的均衡速度越快，储能单元输出功率比值越大，可能导致储能单元输出功率远超其额定功率；当相同时，SOC的变化率之比随着均衡过程中DOC的减小而减小，在DOC逐渐趋近于0时，SOC的变化率之比很小，即均衡速度较慢；当DOC=0时，不同储能单元的SOC变化率之间的比值都保持为1，这意味着无论储能单元的特性如何，它们在充电或放电过程中的SOC变化率相同。

通过上述分析可得：①均衡前期，调节因子受限于储能单元的最大输出功率，越大造成部分储能单元电流越大，导致储能单元输出功率超限；②均衡后期，调节因子受限于均衡速度，越大则均衡速度越快。两者存在矛盾，因此不可取固定值。

由式（7）可得，储能单元的容量会影响SOC的变化，由于制造差异、老化、充放电循环、充放电深度及工作环境和温度等因素的综合影响，导致储能单元的容量不同，在实际运行中，还需采取相应的控制策略，以均衡不同容量储能单元之间的SOC，确保系统可靠运行。

综上所述，固定调节因子SOC均衡控制策略存在以下两个主要局限：①快速均衡存在储能单元输出功率超限的可能，且随着SOC均衡的进行，均衡速度逐渐下降；②未考虑不同储能单元的容量差异，无法确保SOC的均衡效果。

3 改进SOC均衡策略分析

3.1 改进的SOC均衡控制策略

本文重点研究不同容量储能单元的SOC均衡速度和功率分配问题。基于前述章节的分析，为消除不同储能单元间的额定容量ei对SOC均衡的影响，引入相对容量因子m，有

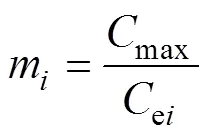
式中，max为所有储能单元中的最大容量。

进而提出改进下垂控制，其下垂系数表达式为

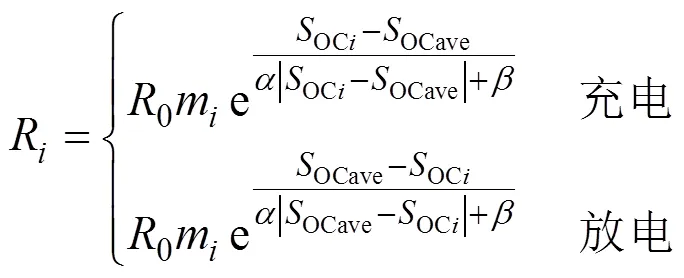
式中：为前期控制因子；为后期加速因子。

当 |DOCi|≥10，即储能单元间的SOC差距较大时，则可忽略，起调整输出功率的作用，从而防止部分储能单元的输出功率超限；当|DOCi|较小时，即储能单元间的SOC差距较小时，则可忽略，起加快均衡SOC速度的作用。

以两个相同容量的储能单元为例，画出下垂系数R与|DOCi|的特性曲线如图5所示，其中0取0.1。由图5可知：在|DOCi|较大时，下垂系数变化比较缓慢，且随着的增加，下垂系数减小；由于是用于后期加速SOC均衡，因此只有使0＜＜1，才能在DOCi较小时起到放大DOCi的作用，且随着的减小，后期均衡速度提高，但过小时系统会发生抖振，导致系统不稳定，因此经过仿真试验选取 =0.02，能够保证系统的稳定运行且SOC快速收敛。

图5 下垂系数Ri与|DSOCi|的特性曲线

当两个储能单元进行放电时，通过联立式（1）、式（2）和式（11）可得

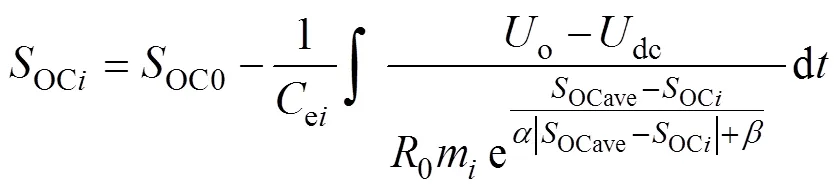
式中：dc为变流器的输出电压；o为变流器的给定初始电压。

则两个储能单元的SOC差值为

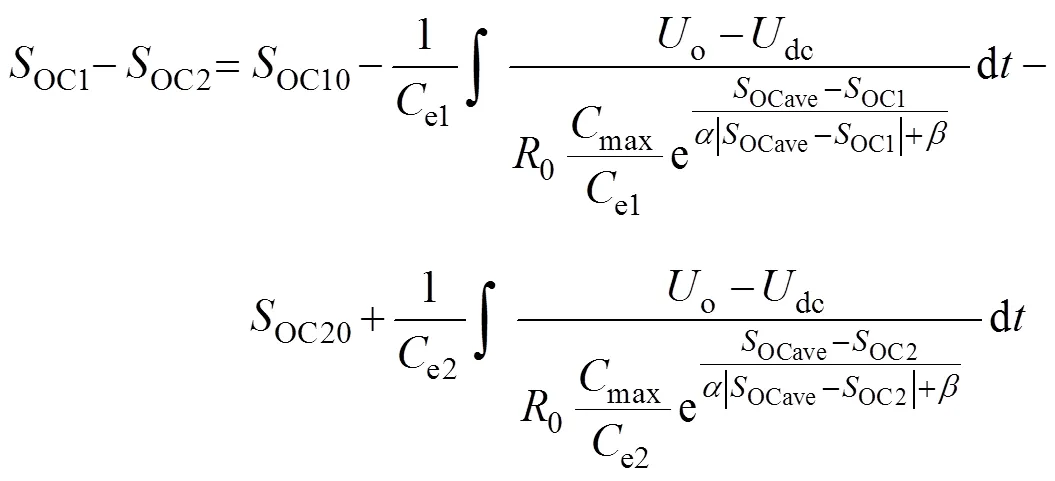
对式（13）求导，得

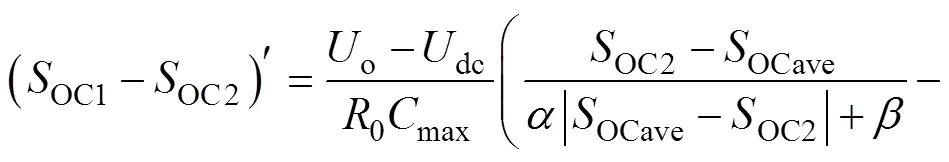
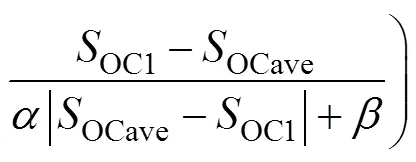
由式（15）可得，若OC1＞OC2，则两者差值的导数小于0，储能单元间的SOC差值逐渐减小，直到均衡状态。相对容量因子的引入使SOC的变化率与储能单元的容量无关，可实现储能系统中的功率按容量比进行合理分配，从而消除容量对SOC均衡的不利影响。

3.2 负荷电流精确分配

由式（3）可知，SOC均衡控制受线路电阻和本地负载波动的影响，为了增强电路的电流分流精度，需要降低线路电阻和本地负载变化对分流准确性的影响。为此，引入等效的参考输出电流，以调整储能单元的输出电流、消除SOC均衡误差并确保母线电压始终保持在合理范围内。

各储能单元的虚拟压降U为

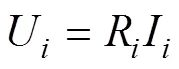
将平均虚拟压降ave作为参考值，有

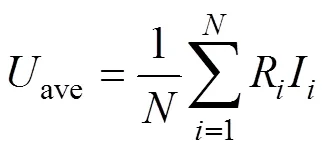
式中，为系统中储能单元总数。

两者的差值经过PI控制器，得到第个储能单元的dci补偿量Du1为

式中，p1、i1为PI控制器参数。

在PI调节器的补偿下，各储能单元的虚拟压降逐渐接近作为参考值的下垂控制虚拟压降，则可 实现

式中，R、R和I、I分别为储能单元、的下垂系数和输出电流。

即间接克服了线路阻抗对电流分配的影响，实现电流的精准分配，则有

3.3 直流母线电压补偿

在分布式储能单元的充放电过程中，往往会出现实际母线电压与额定值之间存在显著差异的情况。为了确保母线电压维持在适当范围内，通过PI控制器，引入母线电压补偿Du2为

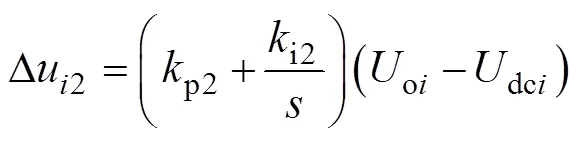
式中，p2、i2为PI控制器参数。

3.4 动态一致性算法

为了降低系统通信负担和经济成本，增强直流微电网控制的稳定性，采用一致性算法估算所需的平均值

式中：=[OCiU]为节点本地测得的信息；()为节点在第次迭代时对于全局平均值的估算；()为第次迭代时节点与节点之间估计结果的累计误差；v为与节点进行通信交互的所有节点集合；a表示节点与节点之间有无通信链路，a=1表示有通信，a=0表示无通信；为通信联系权重。考虑系统的稳定性与收敛性，选取为

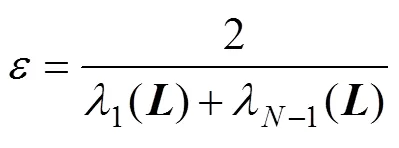
式中：为无向强连通图的拉普拉斯矩阵；()为矩阵的第大特征值，=1,2,…,。

节点的入度d指以该节点为终点的有向边的数量，其表达式为

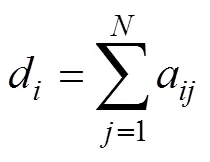
无向强连通图拉普拉斯矩阵=(l)×N的元素为

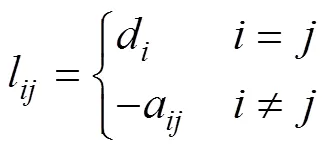
通过动态一致性算法，根据式（25）可知，通信节点之间只需与其相邻节点交流信息，从而可有效减轻通信线路的负担。

3.5 通信故障

系统发生通信故障会导致某些储能单元无法与其相邻单元进行信息交互，因此提出一种通信故障时的下垂控制方法，以实现发生通信故障的储能单元间SOC控制。设置通信故障时的下垂系数ki为

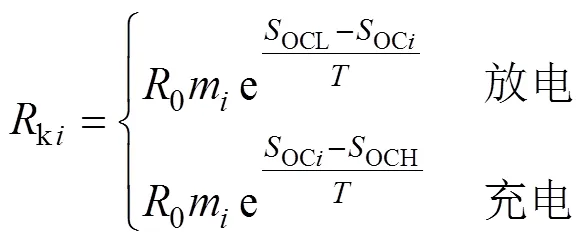
式中：OCH、OCL分别为SOC值的上限、下限；为控制参数。为确保锂电池的稳定运行并延长其使用寿命，在分布式储能系统中，需要限制锂电池的荷电状态在[0.2, 0.9]范围内。当超过所设定的上、下限，该储能单元不参与系统的充放电过程。

放电模式下两个储能单元的SOC差值的导数为

考虑e一阶泰勒级数展开式得

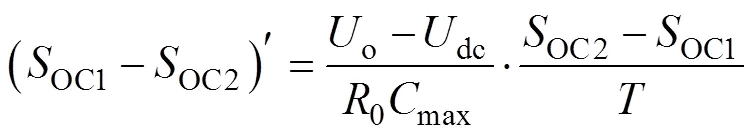
由式（28）可得，若OC1＞OC2，则两者差值的导数小于0，两储能单元的SOC差值逐渐减小，直到均衡状态。因此，发生通信故障的储能单元间仍可通过式（26）实现SOC的均衡，无需通信进行自身的充放电。

3.6 能量控制策略

基于前述分析，本文提出改进的储能单元SOC均衡控制策略，表达式为

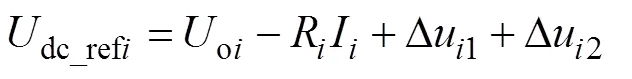
式中，dc_refi为第个变流器的参考输出电压。

系统整体结构如图6所示，包含通信层、改进的下垂控制层和直接控制层。

1）通信层：通信层使用低带宽的通信通道来与相邻单元节点交换储能单元的SOC和虚拟压降等平均值估算数据，并使用动态一致性算法，使数据趋于一致，输出系统实际的SOC平均值和虚拟压降平均值。

2）下垂控制层：利用虚拟压降平均值通过PI调节得到电压补偿量Du1，利用母线电压与额定值的差值得到电压补偿量Du2，利用OCave得到下垂控制系数R，从而得到输出电压参考值dc_refi。

图6 系统整体结构

3）直接控制层：以dc_refi为电压参考值，实现电压、电流双闭环控制，输出脉宽调制（pulse width modulation, PWM）信号，实现对储能单元的能量 控制。

4 仿真验证

为验证本文提出控制策略的有效性与正确性，基于Matlab/Simulink搭建如图7所示的独立直流微电网简化模型，其中包括一个光伏单元、三个ESU和负载。考虑ESU处于相同容量正常充放电、不同容量正常充放电和通信故障三种工况下，以均衡时间与输出功率为指标，与固定调节因子SOC均衡策略进行对比仿真，仿真参数如下：锂电池电压200V，直流母线电压400V，开关频率10kHz，光伏单元输出功率25kW。通信方式遵循图8所示ESU通信网络拓扑。

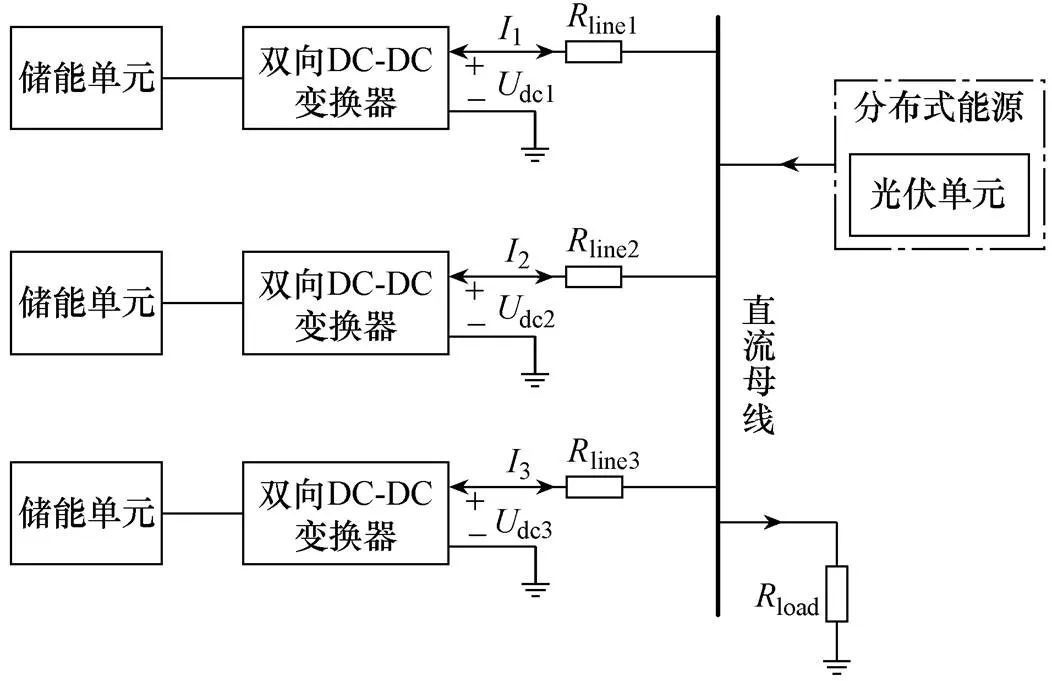
图7 独立直流微电网简化模型

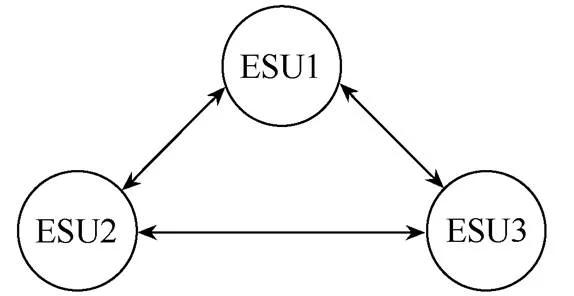
图8 ESU通信网络拓扑

4.1 工况一：相同容量ESU的正常充放电模式

仿真设置负载功率在0～1.5s内为40kW，储能系统处于放电模式，1.5s时负载功率下降至6kW，储能系统进入充电模式，负载功率变化如图9所示。

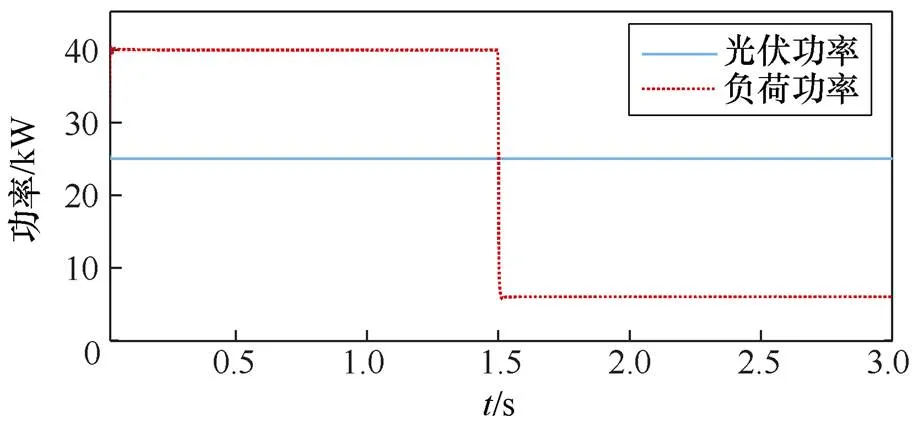
图9 负载功率变化

三组ESU的容量均设置为180A∙h，初始SOC值分别为75%、65%、60%。固定调节因子SOC控制策略不同值的功率和SOC波形如图10所示，其中图10（a）、图10（b）、图10（c）分别为调节因子为5、10、15下的输出功率和SOC仿真 波形。

（a）调节因子=5

（b）调节因子=10

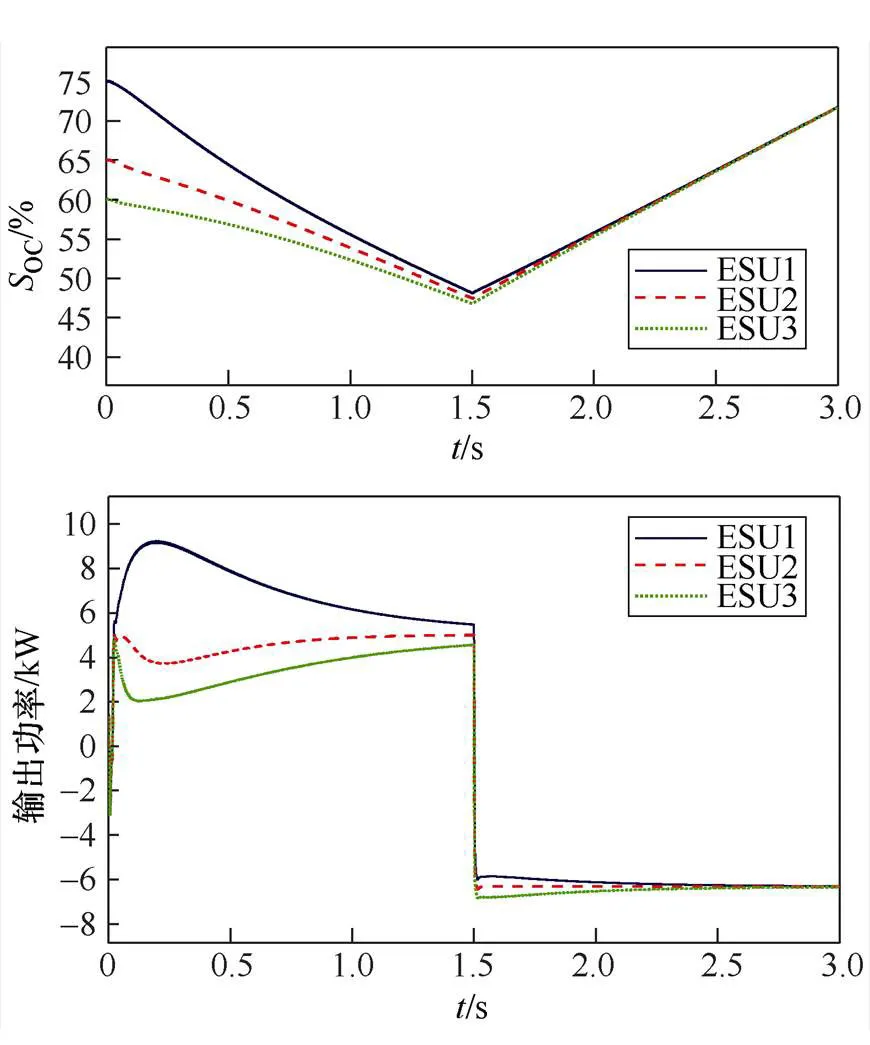
（c）调节因子n=15

由图10可知：图10（a）中系统最大输出功率为6.532kW，在3s内未实现SOC均衡；图10（b）中系统最大输出功率为8.012kW，在3s时实现SOC均衡；图10（c）中系统最大输出功率为9.106kW，在2.5s时实现SOC均衡。固定调节因子SOC均衡策略通过改变调节因子的大小来改变系统的均衡速度，随着调节因子的增大，系统均衡速度加快，但系统的最大输出功率也随之增加，可能会导致输出功率超限。

改进SOC控制策略不同值的SOC、功率及母线电压波形如图11所示，其中图11（a）、图11（b）、图11（c）分别为前期调整因子为1、2、3时的SOC和输出功率仿真波形。

由图11可知：图11（a）中系统最大输出功率为8.864kW，在1.75s时实现SOC均衡；图11（b）中系统最大输出功率为7.065kW，在2.25s时实现SOC均衡；图11（c）中系统最大输出功率为6.612kW，在2.8s时实现SOC均衡。改进SOC均衡策略通过改变前期调整因子来控制系统的最大输出功率，防止最大输出功率超限。较大的前期调整因子导致系统在初始阶段的最大输出功率减小，使系统在初始均衡阶段的输出功率变化更加平稳。与此同时，较小的后期调整因子有助于提高系统在后期均衡阶段的速度，使其更快地达到均衡状态。当负荷功率发生变化时，系统通过调整来迅速使母线电压回到预设数值，保持电压稳定。

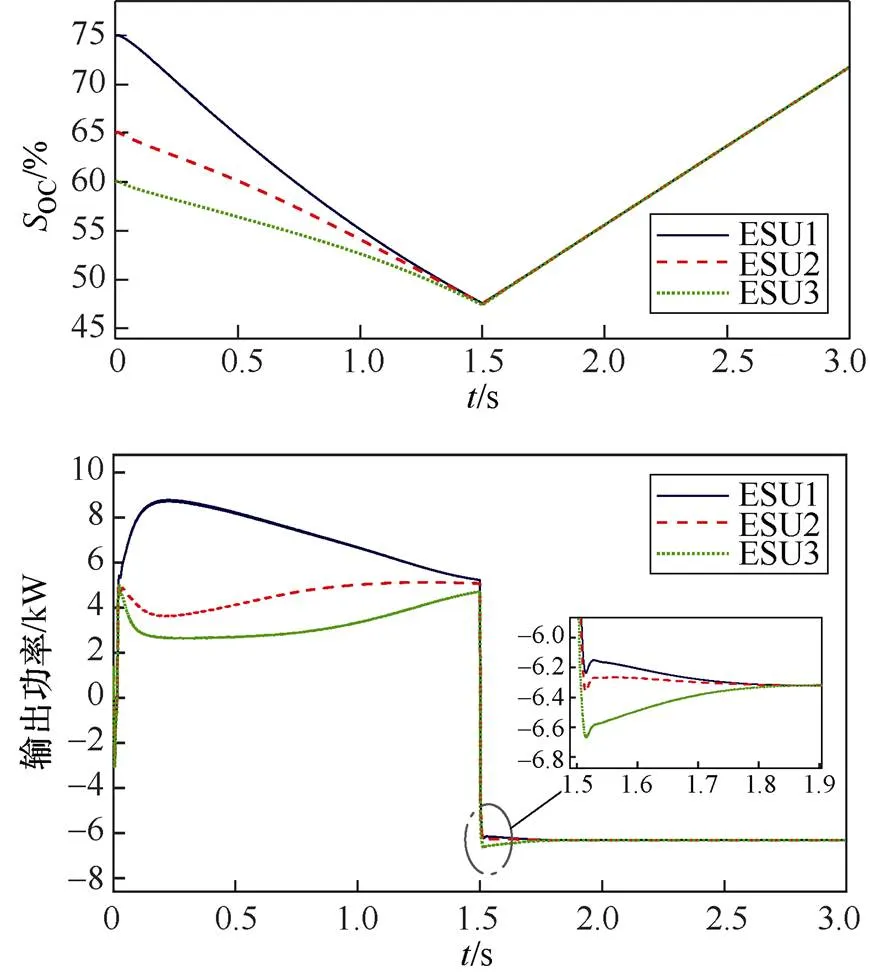
（a）前期调整因子=1

（b）前期调整因子=2

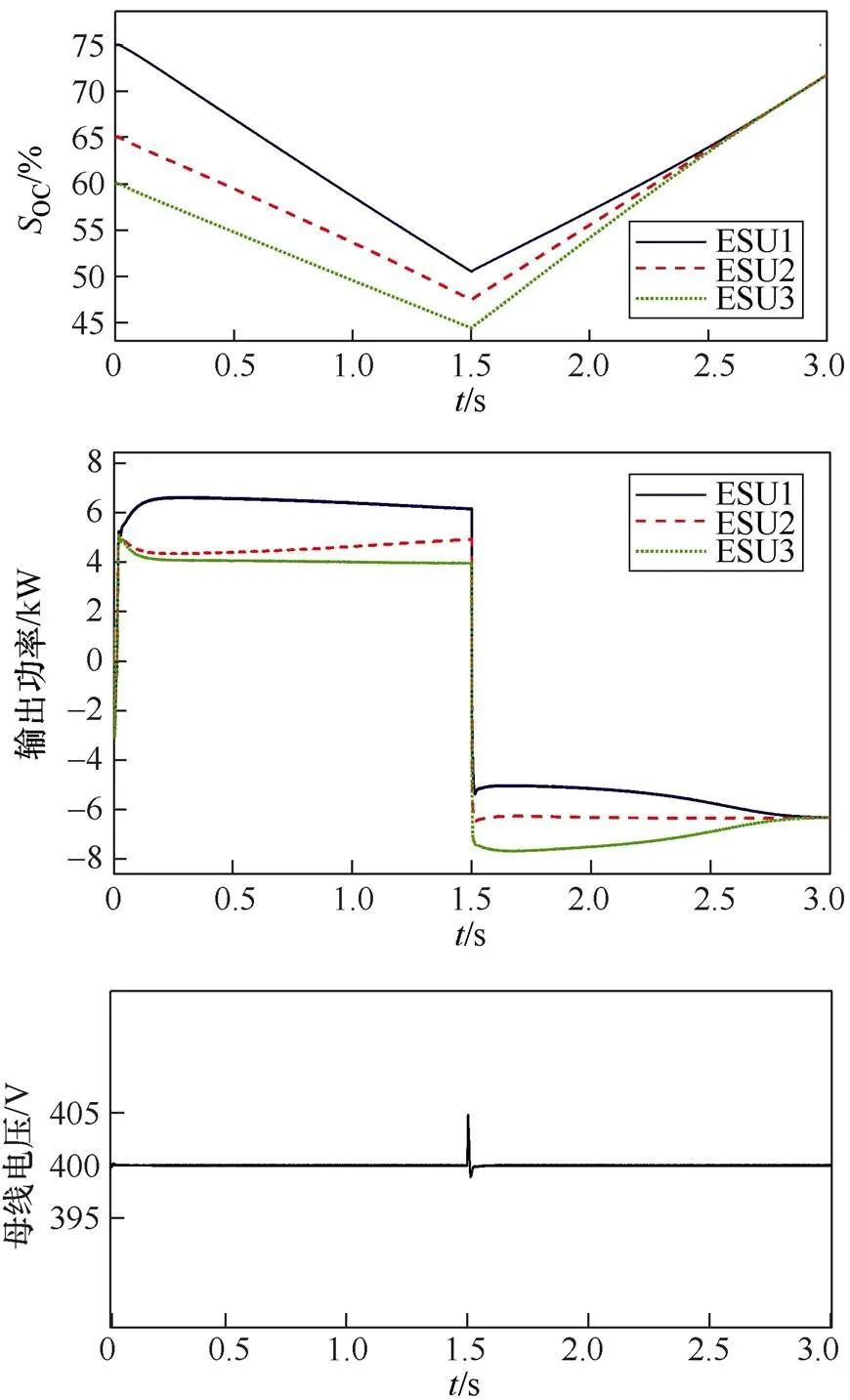
（c）前期调整因子a=3

4.2 工况二：不同容量ESU的正常充放电模式

仿真设置负载功率在1.5s时由40kW突变至6kW，三组ESU的容量分别为180A∙h、150A∙h、120A∙h，容量比为6:5:4，初始的SOC值分别为75%、65%、60%。图12为固定调节因子SOC控制策略调节因子=10的SOC和输出功率波形。

由图12可知：固定调节因子SOC控制策略在系统容量不同的情况下，SOC未能达到均衡，最终系统的输出功率分别为-7.295kW、-6.401kW、-5.265kW，输出功率比例趋于容量比，因此SOC的变化率也趋于相等。随后，无法达到SOC均衡的目的，这与采用固定下垂系数的下垂控制方法产生了类似的结果。

图12 固定调节因子SOC控制策略调节因子n=10的SOC和输出功率波形

图13为改进SOC控制策略前期调节因子为2的SOC和输出功率波形。

图13 改进SOC控制策略前期调整因子a=2的SOC和输出功率波形

由图13可知：改进的SOC均衡控制策略在系统容量不同的情况下，在0～1.5s的放电模式下，ESU1的容量最大且初始SOC值大，SOC下降速度最快，储能单元间的SOC差值在不断减小；1.5s后切换进入充电模式，各储能单元间的SOC增加，但差值仍不断减小，在1.7s时实现SOC的均衡，且系统最终的输出功率分别为-7.596kW、-6.310kW、-5.045kW，比值近似等于容量比6:5:4，实现了输出功率按照各自容量分配的目的。

4.3 工况三：通信故障模式

三组ESU的容量均设置为180A∙h，初始SOC值分别为75%、65%、60%。通信故障时改进SOC控制策略的SOC和输出功率波形如图14所示，在1s时，ESU3通信信号发生故障，ESU3利用式（26）仍能实现稳定放电；在1.5s时，切换到充电模式，ESU1和ESU2的SOC差距逐渐减小，能够实现SOC的均衡，ESU3进行自身充电；在2s时，恢复ESU3的通信功能，重新对三个ESU进行SOC的均衡控制，最终实现SOC趋于一致。

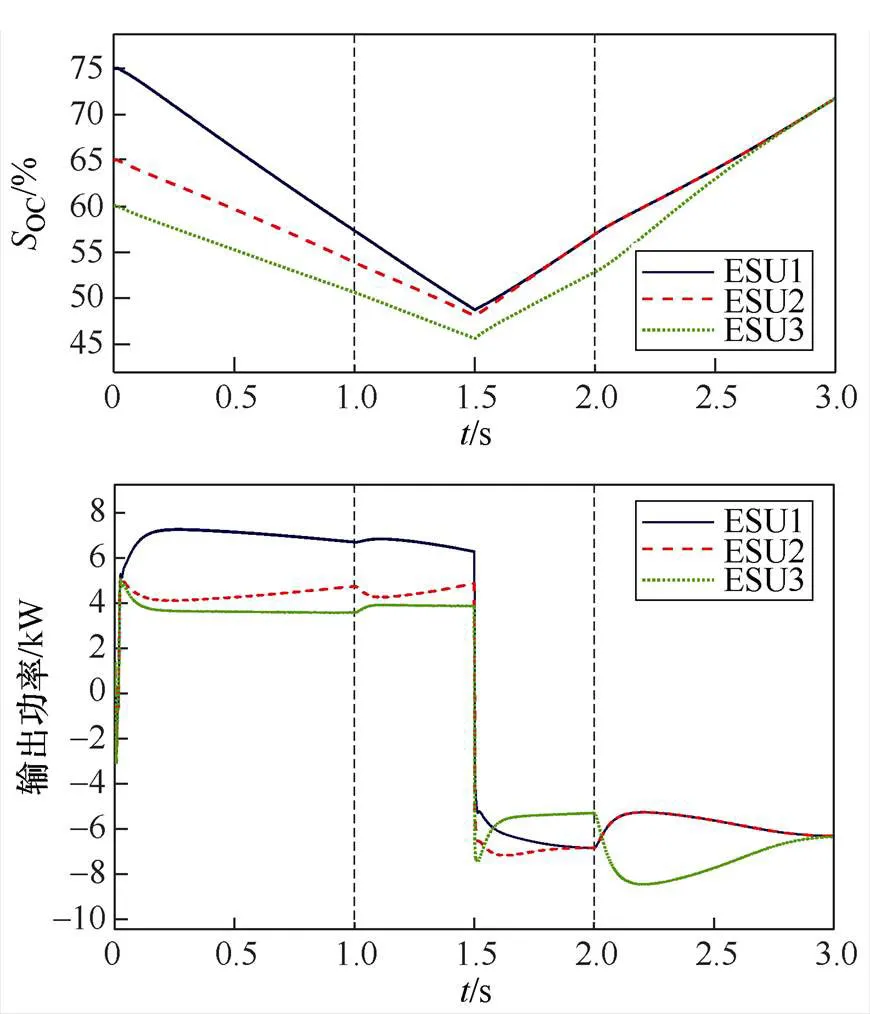
图14 通信故障时改进SOC控制策略的SOC和输出功率波形

5 结论

本文针对固定调节因子多储能单元SOC均衡控制策略存在的均衡速度和输出功率之间的固有矛盾，提出一种变调节因子的不同容量储能系统能量控制策略，理论分析及仿真分析结果表明：

1）以改变下垂系数为基础，通过前期控制因子调节系统最大输出功率，后期加速因子放大均衡后期SOC的差值，能够达到加快SOC均衡的目的。

2）引入容量权重因子，合理分配不同容量储能单元的功率，使其趋于容量比，旨在有效弥补各储能单元间的容量差异，有助于确保各个储能单元在充电和放电过程中的合理参与，提高系统的整体效能和使用寿命。

3）利用动态一致性算法估计全局平均值，能够提高系统的效率、响应速度和可靠性，此外还考虑了通信故障，制定了相应控制策略，使失去通信的储能单元也能稳定地进行充放电，保证系统有效 运行。

[1] 郭慧, 汪飞, 顾永文, 等. 基于电压分层控制的直流微电网及其储能扩容单元功率协调控制策略[J]. 电工技术学报, 2022, 37(12): 3117-3131.

[2] 刘丹妮, 马猛飞. 基于下垂控制的微电网并网转孤网的研究[J]. 电气技术, 2021, 22(2): 21-25.

[3] 李浩琛, 郭志坚. 基于信号补偿下垂控制的微电网动态性能分析[J]. 电气技术, 2022, 23(10): 33-40.

[4] 杨珺, 侯俊浩, 刘亚威, 等. 分布式协同控制方法及在电力系统中的应用综述[J]. 电工技术学报, 2021, 36(19): 4035-4049.

[5] 代广贵, 何晋, 张博嘉. 考虑不同容量的储能SOC均衡与功率分配策略[J]. 电力建设, 2023, 44(6): 12-22.

[6] LI Demin, WU Zaijun, ZHAO Bo, et al. An improved droop control for balancing state of charge of battery energy storage systems in AC microgrid[J]. IEEE Access, 2020, 8: 71917-71929.

[7] 吴青峰, 孙孝峰, 王雅楠, 等. 基于分布式下垂控制的微电网分布式储能系统SOC平衡策略[J]. 电工技术学报, 2018, 33(6): 1247-1256.

[8] HUANG Wangxin, ABU QAHOUQ J A. Energy sharing control scheme for state-of-charge balancing of distributed battery energy storage system[J]. IEEE Transactions on Industrial Electronics, 2015, 62(5): 2764-2776.

[9] XIONG Rui, DUAN Yanzhou. Development and verification of the equilibrium strategy for batteries in electric vehicles[J]. Journal of Beijing Institute of Technology, 2018, 27(1): 22-28.

[10] 续丹, 毛景禄, 王斌, 等. 分布式电池电源模块储能系统的荷电状态均衡控制[J]. 西安交通大学学报, 2019, 53(10): 79-85.

[11] LU Xiaonan, SUN Kai, GUERRERO J M, et al. Double-quadrant state-of-charge-based droop control method for distributed energy storage systems in autonomous DC microgrids[J]. IEEE Transactions on Smart Grid, 2015, 6(1): 147-157.

[12] 杨捷, 金新民, 吴学智, 等. 一种适用于直流微电网的改进型电流负荷分配控制策略[J]. 中国电机工程学报, 2016, 36(1): 59-67.

[13] 李鹏程, 张纯江, 袁然然, 等. 改进SOC下垂控制的分布式储能系统负荷电流分配方法[J]. 中国电机工程学报, 2017, 37(13): 3746-3754.

[14] 方炜, 徐朋, 刘晓东, 等. 直流微网储能系统SoC均衡及电压恢复[J]. 电气自动化, 2019, 41(2): 36-38, 58.

[15] 刘勇, 雷延科, 盘宏斌. 一种直流微电网无母线电压偏移的均衡控制策略[J]. 电力系统保护与控制, 2020, 48(12): 154-161.

[16] 张良, 闫凯宏, 冷祥彪, 等. 基于SOC下垂控制的独立直流微电网协调控制策略研究[J]. 电力系统保护与控制, 2021, 49(12): 87-97.

[17] 樊重阳, 何山. 电流精确分配的直流微网储能单元SOC均衡控制策略[J]. 安徽大学学报(自然科学版), 2022, 46(3): 102-108.

[18] 崔关奇, 刘毅力, 杨茵. 基于指数型下垂控制的改进SOC均衡控制策略研究[J]. 国外电子测量技术, 2023, 42(3): 66-73.

[19] 刘彦呈, 庄绪州, 张勤进, 等. 基于虚拟频率的直流微电网下垂控制策略[J]. 电工技术学报, 2021, 36(8): 1693-1702.

[20] 姚卫波, 徐晔, 黄克峰, 等. 基于前馈解耦的交直流混合微电网双向AC-DC变换器控制策略研究[J]. 电气技术, 2022, 23(5): 25-33.

[21] 朱珊珊, 汪飞, 郭慧, 等. 直流微电网下垂控制技术研究综述[J]. 中国电机工程学报, 2018, 38(1): 72-84, 344.

Energy control strategies for lithium battery energy storage systems with different capacities based on variable regulating factors

YAN Renwu1,2JIANG Xueer1

(1. School of Electronic, Electrical Engineering and Physics, Fujian University of Technology, Fuzhou 350118; 2. Fujian Provincial University Engineering Research Center for Simulation Analysis and Integrated Control of Smart Grid, Fuzhou 350118)

To achieve state of charge (SOC) balancing control and power allocation of energy storage units (ESUs) with different capacities, an energy control strategy with variable regulation factors for energy storage systems with different capacities is proposed. By establishing an exponential function that introduces a capacity factor, each ESU allocates output power according to its capacity ratio, while setting a dynamic adjustment factor to increase as the difference between the SOC of each ESU and the global SOC average decreases, solving the problem of the imbalance between maximum output power and equilibrium speed. To reduce communication pressure, a dynamic consistency algorithm is used to obtain the global average value and develop a control strategy in case of communication failure, so that the system can operate stably. Finally, the Matlab/Simulink simulation is conducted, and the results show that the proposed strategy has faster equalization speed and more accurate power allocation compared to the fixed adjustment factor SOC equalization strategy.

lithium battery energy storage system; energy control; balancing technology; different capacities

国家自然科学基金资助项目（51677059）

2023-10-12

2023-11-23

鄢仁武（1981—），男，博士，副教授，研究方向为柔性直流输电网故障保护、微电网协调控制技术。