基于黑潮流场背景的水下滑翔机运动控制仿真

马玉印 ,王岩峰 ,官 晟 ,王 娜 ,5,丁军航

(1.青岛大学 自动化学院,山东 青岛,266071;2.自然资源部 第一海洋研究所,山东 青岛,266061;3.自然资源部 海洋环境科学与数值模拟重点实验室,山东 青岛,266061;4.山东省海洋环境科学与数值模拟重点实验室,山东 青岛,266061;5.山东省工业控制技术重点实验室,山东 青岛,266071;6.康复大学 康复科学与工程学院,山东 青岛,266113)

0 引言

水下滑翔机是一种通过净浮力驱动的自主水下航行器,具有低功耗、长航程、制造和维护成本低等优点,适用于执行大范围、长时间以及三维连续的水下数据收集任务。1989 年,美国海洋学家Stommel 首次提出水下滑翔机的概念,经过近几十年的发展,其已成为重要的水下移动观测平台之一。目前,一些商业水下滑翔机已广泛应用于各种海洋领域的现场调查,如Slocum[1]、Seaglider[2]、“海燕”[3]和“海翼”[4]等。

近年来,人们利用水下滑翔机对海洋的观测与研究越来越深入,但海洋中普遍存在的各种洋流会对水下滑翔机的运动产生不尽相同的影响,其中黑潮作为全球第二大洋流,具有流速强以及流量大等特征,会对在其中工作的水下滑翔机产生更加严重的干扰,导致水下滑翔机的运动偏离期望运动轨迹,影响其稳定性以及对海洋数据采集的准确性。在以往对水下滑翔机运动控制的研究中,Fan 等[5]通过设计的比例-积分-微分(proportional integral derivative,PID)控制器来校正水下滑翔机在洋流中运动的航向角和俯仰角,从而对运动轨迹进行控制;Bhatta 等[6]提出了一种用来稳定水下滑翔机运动轨迹的非线性反馈控制率;Su 等[7]提出了一种基于自抗扰控制和强化学习的控制策略,用于保证水下滑翔机在洋流中的姿态角稳定,进而控制其运动轨迹;Zhou 等[8]提出了一种基于积分滑模控制和自适应鲁棒时滞控制的双闭环控制结构来对水下滑翔机的有效深度以及姿态进行跟踪控制。但以上轨迹控制研究中未考虑洋流对水下滑翔机运动的影响,或假设的洋流为流速与方向恒定且较小的洋流。

基于上述问题,文中以“海燕II”水下滑翔机为例,首先在考虑受黑潮影响的情况下,根据动量和动量矩定理,建立了“海燕II”动力学模型,并在Simulink 中进行搭建;然后以流速与方向都会随位置变化的HYCOM 黑潮区域数据作为干扰,通过Simulink 仿真分析了黑潮对“海燕II”运动的影响;最后设计了一种基于径向基神经网络的参数自整定PID 控制器,并通过仿真验证了其可以在一定程度上提高“海燕II”在黑潮区域内的轨迹跟踪能力,更好地保证对海洋数据采样的准确性。

1 水下滑翔机动力学建模

1.1 坐标系及运动变量定义

为了研究“海燕II”的运动,建立如图1 所示的2 组坐标系统[9]。其中,E-XYZ是以X轴为正北方向,根据右手定则建立的惯性坐标系,B-xyz是以水下滑翔机浮心B为原点建立的本体坐标系。

图1 “海燕II”坐标系定义Fig.1 Coordinate system definition of Petrel-II

在惯性坐标系下,“海燕II”的位置矢量定义为η1=[X Y Z],姿态矢量用欧拉角表示为η2=[θ ϕ ψ],θ、φ和ψ分别表示俯仰角、横滚角与偏航角。在本体坐标系下,角速度矢量定义为Ω=[p q r],速度矢量定义为V=[u v w]。“海燕II”在运动过程中相对于流体的姿态用侧滑角β 与攻角 α来表示。同时,为了方便不同参数在2 个坐标系之间的互相转换,定义本体坐标系到惯性坐标系的坐标变换矩阵为,则惯性坐标系到本体坐标系的坐标变换矩阵为,即

此外,设Kc=[Uc Vc Wc]为惯性坐标系下的黑潮流速,vr=[ur vr wr]是本体坐标系下滑翔机相对于流体的速度,则

1.2 动力学模型搭建

基于上述坐标系统以及运动变量,水下滑翔机在浮心处的速度矢量可表示为[]。同时,在黑潮的影响下,水下滑翔机浮心处的速度矢量在本体坐标系下为[ur vr wr],则根据本体坐标系到惯性坐标系的坐标变换矩阵可知

类似的,本体坐标系中水下滑翔机的角速度矢量Ω=[p q r]也可由欧拉角来表示,即

式(3)～(4)共同构成了“海燕II”的运动学方程。

在考虑洋流的情况下,根据动量和动量矩定理,可得到水下滑翔机的动力学方程[10],并且在考虑到动力学方程的应用与简化后,其动力学方程在本体坐标系下可表示为

式中:Amλ为惯性矩阵,是刚体惯性矩阵与附加质量矩阵的和;Avw为刚体科里奥利力和离心力相关的矩阵;AFM为滑翔机受到的所有外力及力矩之和。“海燕II”的主要几何物理参数如表1 所示,Amλ、Avw与AFM的具体形式可参考文献[10]和文献[11],然后代入式(5)便可得到“海燕II”的动力学方程。式(3)～(5)共同构成了“海燕II”的动力学模型。

表1 “海燕II”主要几何物理参数及数值Table 1 Physical parameters and values of Petrel-II

2 水下滑翔机运动仿真分析

2.1 黑潮区域数据

在季风与海流体系水量变化等各种因素的影响下,黑潮水体的流速、流量以及流轴位置等水文特征会存在年际摆动,季节性变化以及长、短周期变化[12],考虑到黑潮干扰数据选择的合适与否会直接影响仿真结果的准确性，因此使用了在全球海洋预报系统3.1 上所公布的全球再分析数据,该系统由美国海军耦合海洋资料同化系统与全球1/12°混合坐标海洋模式组成,相关数据可以在HYCOM 网址(https://www.hycom.org)中获得。采用2021 年7 月3 日在北纬16°～北纬19°,东经122°～东经125°范围内的黑潮数据,图2 所示为此黑潮数据于零时刻在不同深度处的流速图。

图2 不同深度处黑潮流速Fig.2 Velocity of the Kuroshio at different depths

2.2 黑潮影响下运动仿真分析

由于HYCOM 黑潮区域数据不包括垂面方向上的流速数据,因此文中的黑潮流向只考虑平行于水平面内的情况。假设“海燕II”自吕宋岛东侧东经17.319 9°,北纬123.400 0°附近处开始沿EX轴向正北方向运动,单个剖面运动的仿真周期设为6 000 s,总共进行2 个剖面运动周期的仿真。在有无黑潮干扰情况下“海燕II”的姿态角与运动轨迹仿真对比结果如图3 所示。

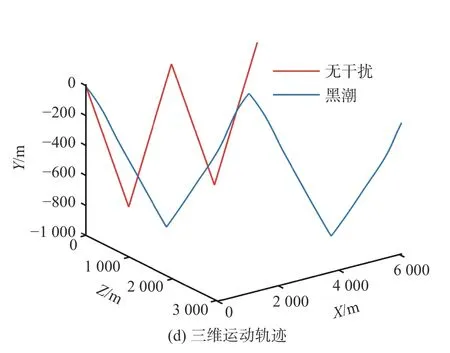
图3 黑潮对水下滑翔机运动的影响Fig.3 Influence of Kuroshio on the motion of Petrel-II

图3(a)展示了“海燕II”在2 个剖面运动过程中所遇黑潮的流速数据,由惯性坐标系下的北向速度与东向速度2 个分量来表示。结合图2 所展示的内容可知,在此次仿真所选择的黑潮流域中,海表附近的黑潮流速最大,约为0.52 m/s,之后随着深度的增加而逐渐降低,最小流速约为0.02 m/s,同时2 个流速分量的变化也表明了黑潮的流向同样会随着深度的变化而不断改变。

图3(b)、图3(c)以及图3(d)分别是“海燕II”的俯仰角、偏航角与运动位置在有无黑潮影响下的仿真对比图。由于黑潮流速的大小与方向会随着深度的变化而改变,从以上对比图中可以看出,“海燕II”的偏航角 ψ在受到黑潮的影响后会发生显著变化,运动轨迹也会向东偏移,ψ出现在黑潮流速最大的海表附近约为-0.722 6 rad,与黑潮的最大偏移角近似相等,水平位移距离也在2 个仿真周期内增加了1 100 m 左右。同样的,“海燕II”的俯仰角 θ也会在黑潮的影响下而改变,特别是在黑潮流速最大的海表附近时,θ受到的影响最大,会由无干扰时的±0.518 5 rad 降低到±0.270 6 rad,但下潜深度不但没有因为θ的降低而减小,反而会在黑潮的影响下增大。综上分析,黑潮会对水下滑翔机的运动产生严重的干扰,影响对所需海洋信息的采样精度,因此需要对黑潮区域中工作的水下滑翔机进行一定的运动控制。

3 水下滑翔机控制器设计

3.1 RBF-PID 控制器设计

目前,水下滑翔机航向控制器主要采用PID控制器[13],然而该控制器是一种线性控制器,因此对于具有非线性和复杂动力学的水下滑翔机而言,有时无法达到预期中的控制效果,并且PID 控制器需要对参数进行反复的设定与调整,过程较为繁琐,加之在流速大小与方向都不断变化的黑潮干扰下,传统PID 控制算法的缺点进一步体现。而径向基函数(radial basis function,RBF)神经网络具有快速逼近任意非线性函数的性质,且拥有良好的泛化能力[14],因此被广泛应用于非线性控制领域,其网络结构如图4 所示。故可以将两者相结合,构成RBF-PID 控制器来对“海燕II”的运动轨迹进行控制。

图4 RBF 神经网络结构图Fig.4 Structure of the RBF neural network

图4 中的RBF 神经网络共有3 层网络结构。第1 层为输入层,设x=[x1,x2,···,xn]T为输入向量。第2 层为隐含层,通常采用RBF 作为激活函数,文中隐含层共有6 层且RBF 采用高斯函数,即

式中:bj为第j个节点的基宽参数;cj为第j个节点的中心向量,cj=[cj1,cj2,···,cji,···,cjn],其中cji为第j个神经元对应于输入层第i个神经元的中心参数。第3 层为输出层,设隐含层到输出层的权值向量w=[w1,w2,···,wm]T,则辨识网络的输出为

在对RBF 神经网络进行训练时,首先赋予权值w随机数,然后通过梯度下降算法得到权值wj、基宽参数bj以 及节点中心cji,并依次采用式(8)来计算RBF 神经网络的代价函数

式中:y(k)为实际输出;y0(k)为神经网络辨识输出。

利用梯度下降法来迭代输出权重wj、节点基宽参数bj与 节点中心cji[15],有

式中: η是学习效率;α是动量因子。

假设姿态角的控制误差为

设计RBF-PID 控制器的输出为

式中:kP=kP0+ΔkP,kI=kI0+ΔkI,kD=kD0+ΔkD,各参数的调整量利用梯度下降法来获得,即

以上便是将RBF 神经网络与PID 控制相结合的方法。在对参数进行初始化后,首先通过式(9)～(11)对RBF 神经网络参数进行调整,并计算出Jacobian 信息,之后通过式(14)得到PID控制的调整量,最后将得到的PID 控制器参数应用于控制系统,从而输出新的控制量,重复以上迭代过程以使水下滑翔机按照期望的轨迹来运动。

3.2 控制仿真与分析

由前述分析可得,为使“海燕II”在黑潮区域工作时按照期望的轨迹来运动,可以从偏航运动与纵倾运动2 个方面进行控制。以“海燕II”在无洋流时的运动轨迹作为期望轨迹来验证RBF-PID控制器的控制效果。在仿真参数选择方面,为了保证PID 控制器的稳定,其参数范围由仿真试验得到并在后期进行修正,kP的范围为[0,10],kI的范围为[0,7],kD的范围为[0,4]。RBF-PID 参数的初值设为kP0=3,kI0=3,kD0=1,学习效率 η=0.5,动量因子 α=0.05,在作为对比的PID 控制方法中,偏航运动控制参数设置为kP=6,kI=2,kD=0.5;纵倾运动控制参数设置为kP=3,kI=4,kD=1。

在偏航运动控制中,以“海燕II”在无洋流时的偏航角作为期望角,通过向RBF-PID 控制器输入“海燕II”当前时刻的实际偏航角与期望偏航角之间的误差,来调整尾舵以对“海燕II”的偏航运动进行控制,图5 所示为RBF-PID 控制器与传统PID控制器对于“海燕II”偏航运动控制的对比图;在纵倾运动控制中,同样以“海燕II”在无洋流时的俯仰角为期望角,向RBF-PID 控制器输入“海燕II”的俯仰角与期望俯仰角之间的误差,来调整俯仰重块的位移距离以控制“海燕II”的俯仰姿态,2 种控制方法的仿真对比结果如图6 所示。

图5 偏航运动控制曲线图Fig.5 Curves of yaw motion control

图6 纵倾运动控制曲线图Fig.6 Curves of pitch motion control

从图5 可以看出,传统的PID 控制器由于参数固定,在黑潮流速不断变化的情况下,对偏航角的控制效果较差。图5(a)表明了RBF-PID 控制器可以根据当前黑潮流速的大小来不断地调整PID 控制中的各个参数,以使水下滑翔机当前时刻的偏航角更接近期望的偏航角度,相较于传统PID 控制器对偏航角控制的均方误差下降了49.33%。表2为2 种方法对偏航运动控制的指标对比,从表中也可以看出,RBF-PID 控制器的控制误差优于PID控制,表明结合RBF 神经网络的PID 控制器对“海燕II”的偏航控制效果更好。

表2 偏航运动控制中PID 与RBF-PID 指标对比Table 2 Comparison of PID and RBF-PID index in yaw motion control

从图6(a)可以看出,在RBF-PID 控制过程中,比例作用、积分作用以及微分作用都会随着黑潮流速与期望俯仰角度的变化而改变,特别是在“海燕II”上浮与下潜的切换过程中,PID 控制器在对俯仰角的控制中会出现超调,而RBF-PID 控制器下的俯仰角变化则较为平缓,均方误差也减少了约35.29%,根据图6(c)中的位置对比结果也可以看出,RBF-PID 控制器相较于传统PID 控制器对运动轨迹的控制更好。

此外,从图5 与图6 中也可以看出,在相同仿真时间内,经过RBF-PID 控制器对运动轨迹的控制后,“海燕II”在黑潮影响下的运动距离比无洋流时更远,具体而言,仿真中“海燕II”在单个剖面运动周期内的运动位移增加了26.97%左右。

4 结束语

为了对黑潮影响下的水下滑翔机运动进行控制,首先以“海燕II”水下滑翔机为研究对象建立了其考虑洋流的动力学模型,接着以HYCOM 黑潮区域数据作为干扰,利用Simulink 仿真分析了强流对“海燕II”运动的影响,然后在传统PID 控制器的基础上结合RBF 神经网络设计了RBF-PID 控制器来对“海燕II”的运动轨迹进行控制。仿真结果表明,RBF-PID 控制器相较于与传统PID 控制器具有更高的控制精度,在偏航运动中对偏航角控制的均方误差可降低49.33%,在纵倾运动中可降低俯仰角变换时出现的超调并使之变换过程更加平稳,能够更好地完成对水下滑翔机在黑潮区域内的运动轨迹控制。由于黑潮变化多样,在对RBF-PID控制器的效果进行验证时只利用了1 组HYCOM黑潮区域数据,并未对在不同黑潮流域内的控制效果进行验证。下一步将对RBF-PID 控制器的自适应能力进行验证,同时考虑水下滑翔机的组队策略以及新的控制策略。